# Leetcode刷題學習筆記 -- 解題技巧
## 從後面往前統計
### [1010. Pairs of Songs With Total Durations Divisible by 60(Medium)](https://leetcode.com/problems/pairs-of-songs-with-total-durations-divisible-by-60/)
給你一個vector<int> time,找出i < j 且 (time[i]+time[j]) % 60 == 0。
> 1. 找出pair 且 i < j,說明了,==如果我找到j,則可以往前用已經統計過i的數值。==
> 2. 所以只要O(N) 就可以,不需要全部找完後再回頭檢查那些pair符合。
```cpp=
int numPairsDivisibleBy60(vector<int>& time) {
int rtn{0};
vector<int> cnt(60, 0);
for(auto& t : time) {
int tt = t % 60;
if(tt == 0) rtn += cnt[0];
else rtn += cnt[60 - t % 60];
cnt[tt]++;
}
return rtn;
}
```
## 從簡單的case開始延伸
例如題目給你一個input的長度,可以從length = 1開始推到n
### [22. Generate ParentheseMed](https://hackmd.io/231S57V1QcmoVFfMr2c5_A#22-Generate-ParenthesesMedium)
### [79. Word Search](https://hackmd.io/h4ghhABcT9yyDC0JcSPRPw#79-Word-SearchMedium)
## 從答案的範圍中,假設答案,驗證答案的正確性。
可以反推從答案的範圍中,選一個值(通常使用binary search),才可以降低搜尋的次數(O(logN), N為答案的範圍)。
[Leetcode刷題學習筆記–Binary Search](/u7dufNJ-SAq7z0WmS-Semw)
```cpp
int left = ANS_MIN, right = ANS_MAX;
while(left < right) {
int mid = left + (right - left) / 2;
// 計算由mid得到的答案是否正確
// 由題目設計下一個left和right的位置
}
```
## 從例外開始思考
可以從例外開始思考,看看有沒有想法。
例如 [556. Next Greater Element III](/gg-708HfRomJ66P7XX_QKQ#556-Next-Greater-Element-III),從完全沒有答案的例子開始,什麼樣的情況是沒有答案?回推怎樣的情況才會開始有答案。
## 犧牲space換來答案的正確
答案正確比浪費的空間還重要。當沒有想法的時候不然浪費一點空間換來答案的正確性。
### [1089. Duplicate Zeros](https://leetcode.com/problems/duplicate-zeros/)
在原本的vector上,如果遇到0,就在0的右邊補上一個0。
例如:[1,0,2,3,0,4,5,0] -> [1,0,0,2,3,0,0,4]
```cpp
// 比起浪費的空間,答案正確比較重要
// 使用比較大的空間來儲存答案
// 可以套過pointer的方法來不使用到額外的空間
void duplicateZeros(vector<int>& arr) {
int sz = arr.size();
int i = sz - 1, j = i + count(arr.begin(), arr.end(), 0);
for(;i >= 0; --i) {
if(arr[i] == 0) {
if(j < sz)
arr[j] = arr[i];
j--;
}
if(j < sz)
arr[j] = arr[i];
j--;
}
}
```
## 方法簡單不會出錯即可
有時候我會拘泥於比較複雜的方法,導致不容易寫出正確的程式。仔細想想,就跟上面的心得一樣,有時候正確性會比酷炫的方法或是浪費space的方法還重要。甚至暴力破解也會比沒解法或是解法錯誤來的好。
### [143. Reorder List](https://leetcode.com/problems/reorder-list/)
重新排列list從原本的L0->L1->L2->L3 變成 L0->L3->L1->L2
> 1. 一開始我想用recursive來做,但是過於複雜容易寫出錯的程式碼。
> 2. 其實只要用stack把node全部存起來,就會有簡單的解法。
```cpp
void reorderList(ListNode* head) {
ListNode *p = head, *np;
stack<ListNode *> st;
while(p) {
st.push(p);
p = p->next;
}
p = head;
for(int i = st.size() / 2; i > 0; --i) {
np = p->next;
p->next = st.top(); st.pop();
p->next->next = np;
p = np;
}
p->next = nullptr;
}
```
## 想想答案的反向
有時候很難想出一個好的解法,其實可以想想反向答案。
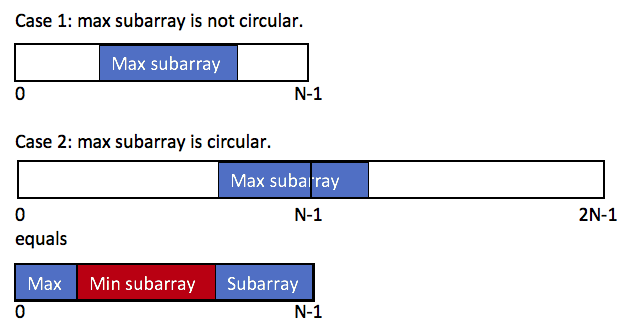
### [918. Maximum Sum Circular Subarray](https://leetcode.com/problems/maximum-sum-circular-subarray/)
找出最大的subarray(連續的元素)和。因為是circular所以可以接到前面,只要元素不重疊。
> 1. 最大subarray和,且可以接到circular等於是找出最小的subarray和。
> 2. (max subarry sum) = total - (min subarray sum)
```cpp
int maxSubarraySumCircular(vector<int>& nums) {
int total, maxsum , curmax, minsum, curmin;
total = maxsum = curmax = minsum = curmin = nums[0];
for(int i = 1; i < nums.size(); ++i) {
curmax = max(curmax + nums[i], nums[i]);
maxsum = max(maxsum, curmax);
curmin = min(curmin + nums[i], nums[i]);
minsum = min(minsum, curmin);
total += nums[i];
}
// 因為如果maxsum為負數,minsum會更負。導致total - minsum會更大
return maxsum > 0 ? max(maxsum, total - minsum) : maxsum;
}
```
### [1658. Minimum Operations to Reduce X to Zero](https://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/)
一開始看到了minimum operrations,就使用了DP結果TLE。看了hints,因為只能從最左和最右刪除,所以最後只會剩下subarray,所以問題就可變成找出最長的subarray,則sz - subarray.size() 就會是minimal operations。
下面的解法是用prefix sum + hash table。
time complexity : $O(N)$
space complexity : $O(N)$
```cpp=
int minOperations(vector<int>& nums, int x) {
int sz = nums.size();
int total = accumulate(nums.begin(), nums.end(), 0);
if(x > total) return -1;
if(x == total) return sz;
int target = total - x;
unordered_map<int, int> m;
m[0] = -1;
int sum = 0, maxlen = 0;
for(int i = 0; i < sz; ++i) {
sum += nums[i];
if(sum >= target && m.count(sum - target))
maxlen = max(maxlen, i - m[sum - target]);
m[sum] = i;
}
return maxlen > 0 ? sz - maxlen : -1;
}
```
以下是two points的解法,個人覺得應該比prefix sum還慢但是leetcode判斷出來是比較快。
```cpp=
int minOperations(vector<int>& nums, int x) {
int sz = nums.size();
int total = accumulate(nums.begin(), nums.end(), 0);
if(x > total) return -1;
if(x == total) return sz;
int target = total - x, left = 0, sum = 0, maxlen = 0;
for(int right = 0; right < sz; ++right) {
sum += nums[right];
while(sum > target)
sum -= nums[left++];
if(sum == target)
maxlen = max(maxlen, right - left + 1);
}
return maxlen > 0 ? sz - maxlen : -1;
}
```
## 從沒有例外,推到題目的情況
### [665. Non-decreasing Array](https://leetcode.com/problems/non-decreasing-array/)
給你一個vector,允許你修改一個數值,問這個vector是不是non-decreasing array(就是後面的數值只會大於等於前面的數值)。
> 1. 先列出 non-decreasing array
> 2. 判斷方法是nums[i] < nums[i - 1], 並且用一個cnt紀錄使否修改過。
```cpp=
int cnt = 0;
for(int i = 1; i < nums.size(); ++i) {
if(nums[i] < nums[i - 1]) {
if(cnt) return false;
cnt++;
}
}
```
> 3. 有noise, 有一個點特別高或是特別低
> 4. 特別低,就是移除nums[i]
> 5. 特別高,就是移除nums[i - 1],因為剛剛的判斷會在特別高的下一個點才發生。
> 6. 從vector中移除element的成本很高,所以使用取代的
> 7. 如果都是用nums[i] = nums[i - 1]來取代,會有一種special case,所以必須判斷nums[i - 2]是否小於等於nums[i]

```cpp=
bool checkPossibility(vector<int>& nums) {
int cnt = 0;
for(int i = 1; i < nums.size(); ++i) {
if(nums[i] < nums[i - 1]) {
if(cnt) return false;
if(i == 1 || nums[i - 2] <= nums[i]) nums[i - 1] = nums[i];
else nums[i] = nums[i - 1];
cnt++;
}
}
// time : O(N)
// space : O(1)
return true;
}
```
## 拼湊題目要的答案
有時候題目要的答案不容易拼湊到,導致寫的程式碼過於奇怪,因為要一次就得到答案。其實只要有辦法拼湊回來,應該是先照程式方便寫的方向。
### [2096. Step-By-Step Directions From a Binary Tree Node to Another](https://leetcode.com/problems/step-by-step-directions-from-a-binary-tree-node-to-another/)
> 1. 先找出從root到startValue和destValue的path
> 2. 移除從root到LCA的相同路徑
> 3. 拼湊答案,start path轉換成連續的U,反轉dest path
```cpp=
bool find(TreeNode *root, int val, string& path) {
if(!root) return false;
if(root->val == val) return true;
bool rtn = false;
if(find(root->left, val, path)) {
path.push_back('L');
rtn = true;
}
if(find(root->right, val, path)) {
path.push_back('R');
rtn = true;
}
return rtn;
}
string getDirections(TreeNode* root, int startValue, int destValue) {
string sp, dp;
find(root, startValue, sp);
find(root, destValue, dp);
// remove the common part before LCA to root
while(!sp.empty() && !dp.empty() && sp.back() == dp.back()) {
sp.pop_back();
dp.pop_back();
}
return string(sp.size(), 'U') + string(dp.rbegin(), dp.rend());
}
```
## 列出所有的case
當沒有頭緒的時候,可以列出所有可能的情況。幫助整理思緒。例如:[838. Push Dominoes](https://hackmd.io/gg-708HfRomJ66P7XX_QKQ?view#838-Push-Dominoes),列出所有可能的骨牌排列:
+ L...L 或是 R...R 兩邊都是一樣,則中間倒的方式一樣。
+ L...R 往兩邊倒,則中間不會改變。
+ R...L 往中間倒,根據中間點數長度,如果為偶數即為RRRLLL,如果為奇數,則為RRR.LLL。
所以程式碼如下:
```cpp
string pushDominoes(string dominoes) {
string rtn{""};
string d = 'L' + dominoes + 'R';
for(int i = 0, j = 1; j < d.size(); ++j) {
if(d[j] == '.') continue;
if(i > 0) rtn += d[i];
int len = j - i - 1;
// case 1
if(d[i] == d[j]) rtn += string(len, d[i]);
// case 2
else if(d[i] == 'L' && d[j] == 'R') rtn += string(len, '.');
// case 3
else rtn += string(len / 2, 'R') + string(len % 2, '.') + string(len / 2, 'L');
i = j;
}
return oss.str();
}
```
## 定義狀態和所有狀態的排列組合
程式是要解決問題。所以必須考慮到所有的可能,才不會有漏掉沒考慮的情況。有時候題目看到沒什麼想法的時候
> 1. 可以先定義有哪些狀態?
> 2. 考慮狀態的排列組合
例如:[968. Binary Tree Cameras](https://leetcode.com/problems/binary-tree-cameras)
> 1. why post-order? 因為必須先知道child的狀態,才可以決定parent的狀態。另外是求最少的camera,所以leaf node不放才可以最少。
> 2. 先定義每個node的狀態。只會有三種,[放置camera,被監視,沒被監視]
> 3. node == nullptr的狀況,定義為monitor,這樣leaf node的狀態才會被轉換成nomonitor。
> 4. 根據child的狀態來決定root的狀態。
> 5. root == nomonitor,因為沒更上層的node,所以必須多放一個camera。
```cpp=
class Solution {
enum st{camera, monitor, nomonitor};
int ans;
int helper(TreeNode* root) {
if(!root) return monitor;
int rtn;
int l = helper(root->left);
int r = helper(root->right);
if(l == nomonitor || r == nomonitor) {
ans++;
return camera;
} else if(l == camera || r == camera) return monitor;
else return nomonitor;
}
public:
int minCameraCover(TreeNode* root) {
int rootst = helper(root);
return rootst == nomonitor ? ans + 1 : ans;
}
};
```
## 資料只有兩種狀態
如果input資料只有兩種狀態,那計算個數是否一樣可以用以下方法。
```cpp
int count{0};
for(auto& n : input) {
if(is_typa_1(n)) count++;
else count--;
}
```
因為資料只有兩種,是否可以用正負來表示。
```cpp
vector<vector<int>> adj;
for(auto& c : connections) {
adj[c[0]].push_back(c[1]);
adj[c[1]].push_back(c[0]);
}
```
### [面试题 17.05. 字母与数字](https://leetcode.cn/problems/find-longest-subarray-lcci/description/)
給你一個vector<string>,輸出最長的subvector使得裡面的字母和數字數量一樣。
> 1. 一開始我想用slinding window但是想一想漏洞很多。
> 2. 後來改用prefix sum但是同時數兩個,也是很多問題。
> 3. 因為只有字母或是數字,可以使用count來加減,因為重點是兩個種類的個數差,至於每種種類有幾個就不是重點。
> 4. 最後就可用prefix sum來求得最長subvector。
```cpp
vector<string> findLongestSubarray(vector<string>& array) {
int count{0};
unordered_map<int, int> m; // count, min index
m[0] = -1;
int len{0}, idx = -1;
for(int i = 0; i < array.size(); ++i) {
if(isalpha(array[i][0])) count++;
else count--;
if(m.count(count) && i - m[count] > len) {
len = i - m[count];
idx = m[count] + 1;
}
if(!m.count(count)) m[count] = i;
}
if(len == 0) return vector<string>();
else return vector<string>(array.begin() + idx, array.begin() + idx + len);
}
```
### [1466. Reorder Routes to Make All Paths Lead to the City Zero](https://leetcode.com/problems/reorder-routes-to-make-all-paths-lead-to-the-city-zero/)
給你一個vector<vector<int>> connections。試問最少需要修正多少的path讓所有的city都可以到city 0。
> 1. 因為路徑是單向的所以可以用"正負"來表示,出node或是進node。
> 2. 使用dfs來判斷需要修正多少的connection。
```cpp=
class Solution {
int dfs(vector<vector<int>>& adj, vector<int>& v, int from) {
int ans{0};
v[from] = 1;
for(auto& next : adj[from]) {
if(!v[abs(next)])
ans += dfs(adj, v, abs(next)) + (next > 0);
}
return ans;
}
public:
int minReorder(int n, vector<vector<int>>& connections) {
vector<vector<int>> adj(n); // from->to
for(auto& c : connections) { // c[0]->c[1]
adj[c[0]].push_back(c[1]);
adj[c[1]].push_back(-c[0]);
}
vector<int> v(n);
return dfs(adj, v, 0);
}
};
```
## 座標轉換
一般vector, array或是string的index都是從0開始。但是從0開始會有一些困擾。例如vector或是array初始化之後都是從0開始。所以可以轉換一下座標,讓index從1開始。這樣再賦予index的時候必須+1。
### [2405. Optimal Partition of String](https://leetcode.com/problems/optimal-partition-of-string/description/)
```cpp=
class Solution {
// 因為為了避開index = 0的情況,所以所有的座標都+1
// original index = 0, 1, 2, 3, 4, 5, 6
// new index = 1, 2, 3, 4, 5, 6, 7
// string = a, b, a, c, a, b, a
// |--|
// left right , 定義為substring內容的最左邊和最右邊
public:
int partitionString(string s) {
int pos[26] = {}, res = 0, left = 0;
for (int right = 0; right < s.size(); ++right) {
// 當char出現在left的右邊的時候,切割字串
if (pos[s[right] - 'a'] >= left) {
++res;
left = right + 1;
}
pos[s[right] - 'a'] = right + 1;
}
return res;
}
};
```
###### tags: `leetcode` `刷題`
 Sign in with Wallet
Sign in with Wallet

