# 2017q3 Homework1 (ternary) ###### tags: `sysprogram` contributed by <`st9007a`> ### Reviewed by `amikai` - [56bc46f](https://github.com/st9007a/balanced-ternary/commit/56bc46f77c912c8a786c83a3a524179e8927a791) 和 [44fe64e](https://github.com/st9007a/balanced-ternary/commit/44fe64ea81d8ee87e2a391ef5e15c65ed788fa9e) 這兩個 commit 使用了註解去區分, 第一個 commit message: Design a struct to represent a 6-trits number, 所以你把 operation 的部份註解, 但是應該要分該 commit， 並不是在下個 commit 再把註解拿掉 - [e0f7b5d](https://github.com/st9007a/balanced-ternary/commit/e0f7b5d8fd64366f8b84fd6524d36a9027c5eaf7) 此 commit messeage: 為 Replace trit struct with unsigned short 但是好像多做了一件事情, 就是在這個 commit 裡實做了 MUX 方法 - 這位同學已經實現了簡單的 3 進位系統, 可惜的是在測試上只用了簡單的方式 - 為什麼要用 inline function (其實是我自己想問的) >> 個人對inline function的理解為，compiler 在編譯時會直接把 inline function 的 assembly code 直接插入呼叫 inline function 的位置，優點是可以減少 function call 的 overhead，缺點是導致執行檔容量變大，所以 inline function 通常會被使用在內容簡短但是會被大量使用的 function，我認為簡單的邏輯運算符合這個情境，故使用 inline function，如果我理解有誤還請指正 >> [name="st9007a"] 這位同學很強, 在報告的撰寫上我不知道有什麼可以挑剔的, 因為寫的比我好太多啦, 所以只能挑細節了 ## [Github](https://github.com/st9007a/balanced-ternary) ## 開發環境 ``` Linux 4.4.0-92-generic Ubuntu 16.04.1 LTS L1d cache: 32K L1i cache: 32K L2 cache: 256K L3 cache: 6144K ``` ## 解釋 Balanced Ternary 原理 ### 簡介 根據 [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)，裡面提到 base-b 的 single digit 可以包含 $log_2 b$ bits 的資訊，而 ternary number system 是 base-3，因此每個 digit 能包含的資訊是 base-2 的 1.58 倍 在 base-3 的系統中，邏輯狀態被劃分為三種 true , false , unknown，這邊可以用表格來統整這三個狀態用數值符號來表示： | true value | unsigned | balanced | | -------- | -------- | -------- | | false | 0 | - | | unknown | 1 | 0 | | true | 2 | + | 這個表格的第二跟三個欄位代表著兩種不同的 base-3 系統，unsigned base-3 就跟我們熟知的十進位制與二進位制概念相似，數值的變動介於 0 到 2 之間，超過 2 就進位，也因為 0 , 1 , 2 無法表示負數，所以 unsigned base-3 跟 base-2 一樣需要一個 leading digit 才有辦法表示負數 而 balanced base-3 將 false 這個狀態定義為 -1，因此在數值上可以很容易的表達負數，以數位邏輯的觀點來看的話，如果要對數值做正負號的轉換的話，只要將原本的數值 -1 跟 1 做交換就行了，也就是做一個 not 的邏輯運算就行了，其中 0 保持不變，相較於 unsigned base-3 跟 base-2 少了一個補數的運算 <br> 附上表格為以 base-3 來表示 $0\sim9$ | decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | | -------- | -- | -- | --- | -- | -- | ----- | -- | -- | -- | -- | | unsigned base-3 | 0 | 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 | | balance base-3 | 0 | + | +\- | +0 | ++ | +\-\- | +\-0 | +\-\+ | +0- | +00 | ### 基本運算 根據 [c2 wiki](http://wiki.c2.com/?ThreeValuedLogic)，將 base-3 的數值系統的基本邏輯運算整理如下 AND | | false | unknown | true | | ------- | ----- | ------- | ------- | | false | false | false | false | | unknown | false | unknown | unknown | | true | false | unknown | true | OR | | false | unknown | true | | ------- | ------- | ------- | ---- | | false | false | unknown | true | | unknown | unknown | unknown | true | | true | true | true | true | NOT | original | NOT | | -------- | ------- | | false | true | | unknown | unknown | | true | false | 上面的表格不特別使用數值的表示法，只要將狀態對映到數值上，無論是 unsigned 或是 balance 都適用上面的表格，透過表格我們也可以更清楚的知道 **unknown** 這個狀態是如何與其他狀態做邏輯運算 > TODO: 詳細閱讀 [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)，理解 base-3 的原理 (並且複習數位邏輯)，整理 base-3 基礎運算操作 > [name="jserv"][color=red] ### 數值轉換 (bal3 to dec) 將 Balanced Ternary 的數值轉換為十進位制的方法與二進位制的概念是一樣的，我們只需將每個位元乘上 $3 ^ n$ ，並將其加總起來 ，其中 $n$ 為該位元在整個數值中的位置，以下為一個簡單的範例，以 `bal3` 小標代表 Balanced Ternary 的數值，`dec` 代表十進位制數值，`T` , `0` , `1` 分別代表的是 false , unknown , true $10_{bal3} = 1 \times 3 ^ 1 + 0 \times 3 ^ 0 = 3_{dec}$ 接著以下是有使用到 `T` 的範例： $1T_{bal3} = 1 \times 3 ^ 1 + (-1) \times 3 ^ 0 = 2_{dec}$ 再來是浮點數的範例： $1T0.T_{bal3} = 1 \times 3 ^ 2 + (-1) \times 3 ^ 1 + 0 \times 3 ^ 0 + (-1) \times 3 ^ {-1} = 6.\overline{3}_{dec}$ 負數的範例，可以很容易的知道只要是由 `T` 開頭便是負數： $T0T1_{bal3} = (-1) \times 3 ^ 3 + 0 \times 3 ^ 2 + (-1) \times 3 ^ 1 + 1 \times 3 ^ 0 = -29_{dec}$ ### 數值轉換 (dec to bal3) 知道了 Balanced Ternary 轉換成十進位制的原理後，試著將十進位制的數值轉為 Balanced Ternary，從 [Wikipedia](https://en.wikipedia.org/wiki/Balanced_ternary#Conversion_to_balanced_ternary_from_any_integer_base) 可以得知轉換的公式如下： $(a_na_{n-1}...a_2a_1.c_1c_2...)_{dec} = \sum_{k=1}^{n}a_k\times10_{bal3} ^ k + \sum_{k=1}^{\infty}c_k \times 10_{bal3} ^ {-k}$ 要使用這個公式必須要有 $0\ \sim\ 10$ 的 Balanced Ternary 表達式，所以這邊先列出來： | Dec | Bal3 | | - | - | | 0 | 0 | | 1 | 1 | | 2 | 1T | | 3 | 10 | | 4 | 11 | | 5 | 1TT | | 6 | 1T0 | | 7 | 1T1 | | 8 | 10T | | 9 | 100 | | 10 | 101 | 有了對照表跟公式後，開始來轉換看看： $34_{dec} = 10_{bal3} * 101_{bal3} ^ 1 + 11_{bal3} * 101_{bal3} ^ 0 = 1010_{bal3} + 11_{bal3} = 11T1_{bal3}$ 可以反向推導來驗證： $11T1_{bal3} = 1 * 3 ^ 3 + 1 * 3 ^ 2 + (-1) * 3 ^ 1 + 1 * 3 ^ 0 = 34_{dec}$ > 乘號 "X" 可以使用 LaTeX 語法中的 `\times` 表示 > [name=課程助教][color=red] ### 運算 > 請閱讀 [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)，關注於 ternary multiplexer, Unary functions, half-adder, Consensus, full adder, Overflow > [name="jserv][color=blue] 接著要探討的是 balanced ternary 如何進行基本的數值運算操作，在此之前先介紹一下接下來會被很常用到的一個數位電路：ternary multiplexer ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/multiplexer.png) 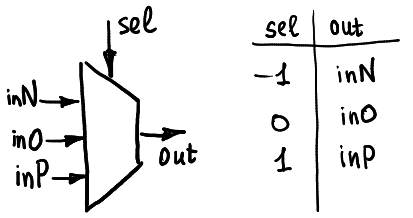這個 multiplexer 與我們一般看到的 multiplexer 不同，它的 in 腳位數量不是 $2^n$ 而是 $3^n$，右邊表格則是這個 multiplexer 輸出的狀態對照表 那這個 multiplexer 有什麼功用呢?只要改變 in 腳位的狀態，multiplexer 會根據不同的狀況而有不同的 unary functions 的功能，關於 unary functions 的解釋可以從 [wikipedia](https://en.wikipedia.org/wiki/Unary_function) 很簡單的理解 <br> 這是一個寫程式很常用到的 unary function，也就是 for loop 中`i++`的 `++` 的運算 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/A%2B1.png) 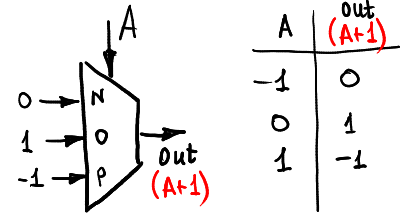同理，下圖是一個 `--` 運算 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/A-1.png) 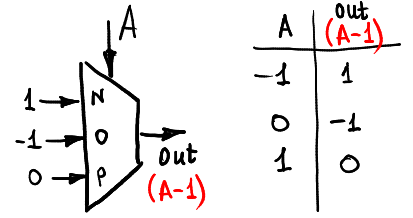下圖所表現的 unary function 為 $max(A, 0)$，也就是輸出 A 與 0 之間何者比較大 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/max(A%2C0).png) 相反的，下圖為輸出 A 與 0 之間何者較小 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/min(A%2C0).png) 有了這四個 unary functions 後，終於可以進入這個小節的重點，也就是數值的運算，下圖是一個 balanced ternary 的半加器電路圖 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/A%2BB.png) 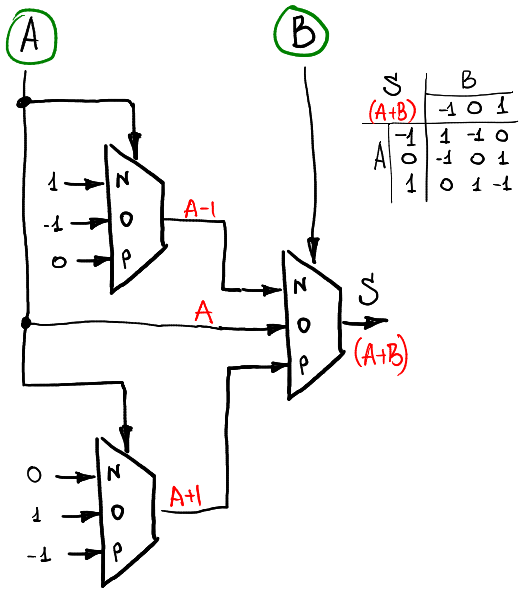它使用到了三個 multiplexer，我們可以把它理解成兩層的結構，第一層輸入為 A 並且做了 unary functions 的運算後輸出給第二層，第二層收到第一層的輸出後根據它的輸入 B 來輸出正確的值 A + B 接著是 consensus 的電路，在 balanced ternary 中我們可以用以下的數學式來表達 consensus function： $f(A, B) = -1\ if\ A = B = -1$ $f(A, B) = 1\ if\ A = B = 1$ $otherwise,\ f(A, B) = 0$ 仔細觀察其實可以發現，這個數學式恰好可以代表 A + B 的進位，以下是電路圖 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/cons(A%2CB).png) 有了半加器後，接著是全加器，全加器看似複雜，其實就是兩個半加器疊起來的架構 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/A%2BB%2BCin.png) 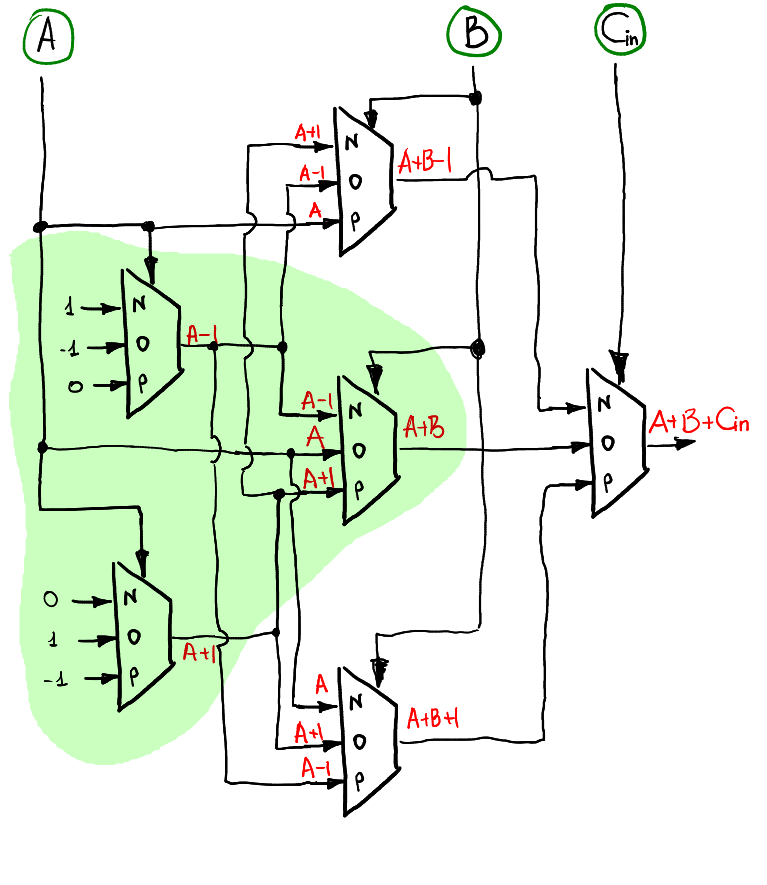overflow則可以由 consensus 電路來做延伸 ![](https://raw.githubusercontent.com/ssloy/tutorials/master/ternary/doc/overflow.png) 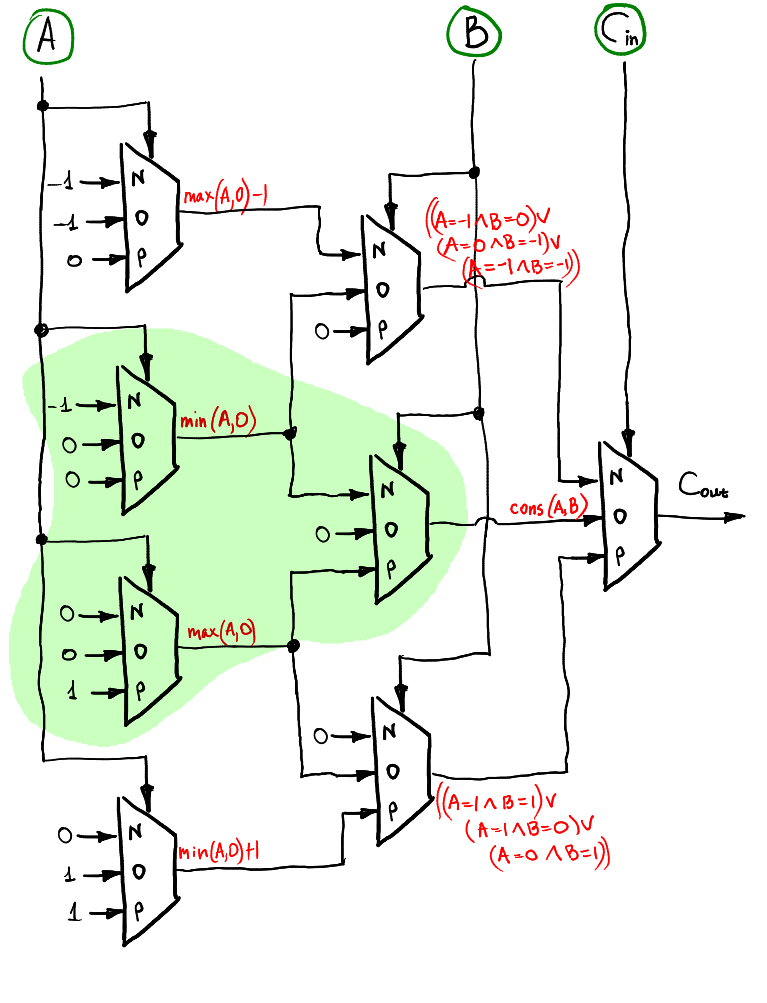到此，balanced ternary 的基本數值運算已經完成了，更複雜的運算都可以從這些電路延伸出去 ### 實作 參考 [youtube -- Build a base 3 computer](https://www.youtube.com/watch?v=EbJMtJq20NY&feature=youtu.be&t=203) 中提到的用兩個 bit 可以呈現一個 trit 的所有狀態，所以決定試著設計一個簡單的 balanced ternary 系統，首先創造一份標頭檔 `ternary.h` ```c #define T_FALSE 2 #define T_UNKNOWN 3 #define T_TRUE 1 typedef unsigned short u_int16; uint16_t AND(uint16_t a,uint16_t b); uint16_t OR(uint16_t a, uint16_t b); uint16_t NOT(uint16_t num); uint16_t DECODE_FALSE(uint16_t num); uint16_t DECODE_TRUE(uint16_t num); uint16_t DECODE_UNKNOWN(uint16_t num); ``` 最上面三行定義了參考影片中 trit 對應到十進位的數字，下面的 function 則是一些基本的邏輯運算，這邊選擇 unsigned short 當作一個 trit，實際上會被用到的只有其中兩個 bit，接著在 `ternary.c` 中實作邏輯運算 ```c inline uint16_t AND(uint16_t a, uint16_t b) { return (a & b & 1) | ((a | b) & 2); } inline uint16_t OR(uint16_t a, uint16_t b) { return ((a | b) & 1) | (a & b & 2); } inline uint16_t NOT(uint16_t num) { return ((~num & 3) | num >> 1) | (num | (~num & 3)>> 1) << 1; } inline uint16_t DECODE_FALSE(uint16_t num) { return (num << 1) | (~num & 1); } inline uint16_t DECODE_TRUE(uint16_t num) { return (num & 2) | ((~num & 2) >> 1); } inline uint16_t DECODE_UNKNOWN(uint16_t num) { return (~(num & ((num >> 1) & 1)) << 1) | (num & ((num >> 1) & 1)); } ``` 考量到邏輯運算都是使用 bitwise operator，同時程式碼也不會太長所以這裡使用 inline function 來實作，有了基本邏輯操作後，接著就能實作出上一節的數位電路 ```c uint16_t multiplexer(uint16_t inN, uint16_t inO, uint16_t inP, u_int16 sel) { uint16_t f = AND(inN, DECODE_FALSE(sel)); uint16_t u = AND(inO, DECODE_UNKNOWN(sel)); uint16_t t = AND(inP, DECODE_TRUE(sel)); return OR(f, OR(u, t)); } uint16_t halfAdder(uint16_t a, uint16_t b) { uint16_t pinN = multiplexer(T_TRUE, T_FALSE, T_UNKNOWN, a); uint16_t pinP = multiplexer(T_UNKNOWN, T_TRUE, T_FALSE, a); return multiplexer(pinN, a, pinP, b); } uint16_t consensus(uint16_t a, uint16_t b) { uint16_t pinN = multiplexer(T_FALSE, T_UNKNOWN, T_UNKNOWN, a); uint16_t pinP = multiplexer(T_UNKNOWN, T_UNKNOWN, T_TRUE, a); return multiplexer(pinN, T_UNKNOWN, pinP, b); } uint16_t fullAdder(uint16_t a, uint16_t b, uint16_t cin) { return halfAdder(halfAdder(a, b), cin); } uint16_t checkOverflow(uint16_t a, uint16_t b, uint16_t cin) { uint16_t maxCompZero = multiplexer(T_UNKNOWN, T_UNKNOWN, T_TRUE, a); uint16_t minCompZero = multiplexer(T_FALSE, T_UNKNOWN, T_UNKNOWN, a); uint16_t maxCompZeroSubOne = multiplexer(T_FALSE, T_FALSE, T_UNKNOWN, a); uint16_t minCompZeroAddOne = multiplexer(T_UNKNOWN, T_TRUE, T_TRUE, a); uint16_t pinN = multiplexer(maxCompZeroSubOne, minCompZero, T_UNKNOWN, b); uint16_t pinO = multiplexer(minCompZero, T_UNKNOWN, maxCompZero, b); uint16_t pinP = multiplexer(T_UNKNOWN, maxCompZero, minCompZeroAddOne, b); return multiplexer(pinN, pinO, pinP, cin); } ``` 程式碼看起來就是在兜電路，然後這裡的變數命名應該還有改善的空間，數位電路有了以後，接著來設計一個 6-trits 的整數結構 ```c typedef struct __TERNARY_INT { unsigned short val:12; } tint6; ``` 由於一個 trit 必須由兩個 bits 才能表現，所以這邊用 unsigned short 的其中 12 個 bits 來當作 6-trits 整數，接著可以試著實作整數的加法，這時候就可以拿出剛剛的寫好的全加器來用 ```c tint6 *sum(tint6 *a, tint6 *b, tint6 *carry) { tint6 *sum = (tint6 *) malloc(sizeof(tint6)); carry->val = T_UNKNOWN; sum->val = 0; for (int i = 0; i < 12; i += 2) { uint16_t tritA = (a->val & (3 << i)) >> i; uint16_t tritB = (b->val & (3 << i)) >> i; sum->val |= fullAdder(tritA, tritB, carry->val) << i; carry->val = checkOverflow(tritA, tritB, carry->val); } return sum; } ``` 再來為了更方便的使用 6-trits 整數，所以設計一個 function 輸入十進位整數回傳 6-trits 整數結構 ```c tint6 *getTernaryInt(int num) { if (num > 364 || num < -364) { printf("%d is out of range.\n", num); return NULL; } int inv = 1; if (num < 0) num *= inv = -1; int step = 0; tint6 *tnum = (t_int6 *) malloc(sizeof(t_int6)); tnum->val = 0; do { uint16_t digit = num % 3; if (digit == 2) { digit = T_FALSE; ++num; } if (digit == 0) { digit = T_UNKNOWN; } if (inv == -1) { digit = NOT(digit); } tnum->val |= (digit & 3) << step; step += 2; num = num / 3; } while(num); tnum-> val |= 255 << step; return tnum; } ``` 這個轉換方法是參考 [github -- balanced ternary](https://github.com/thirdcoder/balanced-ternary/blob/master/bt.js) 的，值得一提的是 6-trits 整數能表達的數值範圍是 $-364\sim364$，比同樣 digit 數量的 base-2 整數多了 10倍左右，最後為了方便 debug，寫了一個能把 6-trits 整數轉回來的 function ```c static int t2b[3] = { 1, -1, 0 }; short toBinary(tint6 *tnum) { short sum = 0; short exp = 1; unsigned short val = tnum->val; for (int i = 0; i < 6; i++) { sum += t2b[(val & 3) - 1] * exp; exp *= 3; val >>= 2; } return sum; } ``` ## 驗證系統 上一節嘗試設計一個簡易的 balanced ternary 系統，接著需要幫系統做單元測試，這邊選用 [libcheck](https://libcheck.github.io/check/) 來做 uint test，主要做的測試有四個：convert , upper bound , lower bound , sum，完整程式碼如下： ```clike #include <check.h> #include <stdlib.h> #include "../ternary.h" START_TEST(test_tint6_eq) { tint6 *t; for (int i = -364; i <= 364; i++) { t = getTernaryInt(i); ck_assert_int_eq(toBinary(t), i); } free(t); } END_TEST START_TEST(test_tint6_out_of_upper_bound) { tint6 *up = getTernaryInt(365); ck_assert_msg(up == NULL, "NULL should be returned on input integer out of range."); } END_TEST START_TEST(test_tint6_out_of_lower_bound) { tint6 *low = getTernaryInt(-365); ck_assert_msg(low == NULL, "NULL should be returned on input integer out of range."); } END_TEST START_TEST(test_tint6_sum) { tint6 *a; tint6 *b; tint6 carry; for (int i = -364; i <= 364; i++) { a = getTernaryInt(i); for (int j = -364; j <= 364; j++) { b = getTernaryInt(j); int total = toBinary(sum(a, b, &carry)) + toBinary(&carry) * 729; ck_assert_int_eq(total, i + j); } } } END_TEST Suite *ternarySuite() { Suite *s; TCase *tCore; s = suite_create("Ternary"); tCore = tcase_create("Core"); tcase_add_test(tCore, test_tint6_eq); tcase_add_test(tCore, test_tint6_out_of_upper_bound); tcase_add_test(tCore, test_tint6_out_of_lower_bound); tcase_add_test(tCore, test_tint6_sum); suite_add_tcase(s, tCore); return s; } } int main() { int number_failed; Suite *s; SRunner *sr; s = ternarySuite(); sr = srunner_create(s); srunner_run_all(sr, CK_NORMAL); number_failed = srunner_ntests_failed(sr); srunner_free(sr); return (number_failed == 0) ? EXIT_SUCCESS : EXIT_FAILURE; } ``` 測試結果如下： ``` Running suite(s): Ternary 365 is out of range. -365 is out of range. 100%: Checks: 4, Failures: 0, Errors: 0 ``` 測試結果全部都有通過 注：其實第一次測試時，在 `test_tint6_sum` 是失敗的，也因為有做單元測試才注意到 sum 在某些時機下會有輸出結果錯誤的 bug ## Balanced Ternary 的設計要解決什麼類型的問題? ### Digit 所能表示的數值範圍 從空間使用的觀點來看，如果單純比較 8 個 digit 的話，base-2 的數值系統可以表現的數字範圍是 unsigned 是 $0\sim 255$，signed 是 $-128\sim127$，不管如何，能表現出來的數值為 256 個，接著 balanced ternary 的數值系統的能表現的數字則有 $1 + 2\times\sum_{k=0}^{7}3^k = 6561$ 個，跟 base-2 相比就可以知道其在空間上的差距 ### Sign digit Balanced ternary 的狀態已經包含 -1，所以如果想要將一個數值作正負號的轉換，只要將裡面每個 digit 乘上 -1，也就是作一個 NOT 的邏輯運算就行，而我們也可以很容易的由數值的最高有效位知道它的正負號，所以可以節省一個 digit 的空間去紀錄 sign ### 浮點數精確度 根據 [Conversión de un número binario a formato IEEE 754](https://www.youtube.com/watch?v=VlX4OlKvzAk) 以及 [wikipedia -- IEEE 754](https://zh.wikipedia.org/wiki/IEEE_754) 同樣以 32-digits 的浮點數來看的話，我們可以知道浮點數的精確度最多可以用 23 個 digits 來表示，可以想像如果要修正浮點數誤差，最多也只能用最小的浮點數來當作修正用的一個單位，所以可以知道二進位制的狀況下，這個修正用的單位大約是 $2^{-23} = 1.1920929e-7$，而 balanced ternary 則是 $3^{-23} = 1.0622118e-11$，所以在浮點數的精確度上，如果使用同樣長度的 digits 那麼 balanced ternary 的精確度大約是 binary 的 10000 倍 ### 實際應用案例 -- IOTA IOTA 是針對物聯網所產生的機器對機器的加密貨幣，而其運作原理與我們熟知的區塊鏈有所不同，這邊可以來複習一下區塊鏈的機制： 1. 每當有一筆新的交易產生，就會廣播給所有節點 2. 收到廣播的節點會把這筆交易紀錄放進一個區塊 3. 接著所有節點會開始驗證這個區塊( proof-of-work ) 4. 當有一個節點驗證完這個區塊(簽上 nonce )，就會把這個區塊廣播給其他所有節點 5. 節點確認區塊是合法後，就會將其放到區塊鏈中，接著開始產生下一個區塊 每個節點都會存在一個區塊鏈，這個區塊鏈將記錄所有的交易，可以想像成區塊鏈就是一個全域的公共帳本，被每個人管理著 #### 機制 IOTA 所使用的技術概念則不同於區塊鏈，而是由一個稱為 Tangle 的 DAG (有方向性且不成環的 graph )構成，Tangle 中的每個 vertex 就是一筆交易，edge 則是每筆交易之間的驗證關係，我們可以從發起交易的機制來更加了解 Tangle 每當一個節點發起一筆交易時，必須要隨機驗證已經存在的其中兩筆交易，而交易 A 驗證交易 B 就可以在 Tangle 上表示成 $A \rightarrow B$，這裡我們稱為**直接驗證**，節點必須直接驗證兩筆已存在的交易才有辦法發起新的交易 當 Tangle 中不存在 $A \rightarrow B$ 但是存在從 A 出發至少經過兩個 edge 可以到達 B，我們成稱為 A **間接驗證**了 B，所以可以想像越多節點發起交易就會有越多交易被直接或間接的驗證，同時存在於 Tangle 的交易紀錄的合法性就越高 #### 驗證 驗證交易的過程就跟區塊鏈的 proof-of-work 類似，必須找到一個 nonce 使其 hash 值達成特定的格式，而可以從[The Tech Behind IOTA Explained](http://www.tangleblog.com/2017/01/25/the-tech-behind-iota-explained/) 最後知道這驗證工作相對於區塊鏈是比較簡單的，若新發起的交易以及驗證的兩筆交易其中兩筆發生衝突時，節點就會利用演算法來決定哪一筆交易要被孤立，被孤立的交易紀錄將不再被間接驗證 由這裡可以知道一個有趣的事實，Tangle中確實可能存在不合法的交易紀錄，而節點之間處於一個非同步的網絡，所以每個節點的 Tangle 可能會有一點不同，但是 IOTA 是可以允許節點間沒有達成共識的，只要遵從一個核心概念：合法的交易紀錄就可以繼續存在 #### 權重 每筆交易紀錄中存在著一個權重，每被直接或間接驗證一次，交易紀錄的權重就會增加，可以透過這個權重可以知道這筆交易紀錄在 Tangle 中的重要性，如下圖所示 ![](http://blogchaincafe.com/wp-content/uploads/2016/07/iotatoken_1.jpg) #### Ternary Processor IOTA 使用了 ternary 的處理器，裡面使用的就是 balanced ternary 的數值系統，從上面討論到的空間使用以及算術精確度，可以知道 ternary processor 更有效率，其 Tangle 以及相關的演算法都是基於 balanced ternary 來設計，舉例來說：驗證工作的所要找的 nonce 大約要檢查 $3^8$ 個隨機數，其原因就是 hash 被要求前幾個 trits 要符合特定格式 #### 分析程式碼 分析 IOTA 在 github 上的開源專案，可以找到 balanced ternary 的蹤跡，參照 iota.lib.js 中的 [/lib/crypto/converter/converter.js](https://github.com/iotaledger/iota.lib.js/blob/master/lib/crypto/converter/converter.js)，這個腳本專門處理 binary 轉 balanced ternary，附上裡面其中一段程式碼： ```javascript var trits = function( input, state ) { var trits = state || []; if (Number.isInteger(input)) { var absoluteValue = input < 0 ? -input : input; while (absoluteValue > 0) { var remainder = absoluteValue % 3; absoluteValue = Math.floor(absoluteValue / 3); if (remainder > 1) { remainder = -1; absoluteValue++; } trits[trits.length] = remainder; } if (input < 0) { for (var i = 0; i < trits.length; i++) { trits[i] = -trits[i]; } } } else { for (var i = 0; i < input.length; i++) { var index = trytesAlphabet.indexOf(input.charAt(i)); trits[i * 3] = trytesTrits[index][0]; trits[i * 3 + 1] = trytesTrits[index][1]; trits[i * 3 + 2] = trytesTrits[index][2]; } } return trits; } ``` 這段程式碼便是將 trytes 轉換成 trits 形式，然後用 JavaScript 的 Array 結構儲存，每個 element 就是一個 trit 另外這支腳本還包含其他轉換的 function，如 trits to trytes , trits to integer value , integer value to trits ## 參考資料 [wikipedia -- balanced ternary](https://en.wikipedia.org/wiki/Balanced_ternary) [FATESAIKOU 共筆](https://hackmd.io/s/H1N168fsZ) [CS3343 -- balanced ternary](http://www.cs.utsa.edu/~wagner/CS3343/ternary/baltern.html) [The Balanced Ternary Machines of Soviet Russia](https://dev.to/buntine/the-balanced-ternary-machines-of-soviet-russia) [c2 wiki -- three valued logic](http://wiki.c2.com/?ThreeValuedLogic) [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics) [wikipedia -- unary function](https://en.wikipedia.org/wiki/Unary_function) [youtube -- Build a base 3 computer](https://www.youtube.com/watch?v=EbJMtJq20NY&feature=youtu.be&t=203) [github -- balanced ternary](https://github.com/thirdcoder/balanced-ternary/blob/master/bt.js) [Conversión de un número binario a formato IEEE 754](https://www.youtube.com/watch?v=VlX4OlKvzAk) [wikipedia -- IEEE 754](https://zh.wikipedia.org/wiki/IEEE_754) [Bitcoin -- A Peer-to-Peer Electronic Cash System](https://bitcoin.org/bitcoin.pdf) [The Tech Behind IOTA Explained](http://www.tangleblog.com/2017/01/25/the-tech-behind-iota-explained/) [Tangle 繁體中文白皮書](https://hackmd.io/c/rkpoORY4W/https%3A%2F%2Fhackmd.io%2Fs%2FB1YKzhbLb%23) [github -- iota.lib.js](https://github.com/iotaledger/iota.lib.js)