# 2017q3 Homework8 (ternary)
contributed by <`FATESAIKOU, FENG270`>
## Balanced Ternary 簡介
Balanced Ternary,中文稱作平衡三進制,如其字義本身是一個用來表示數值的系統。但相對於其他的數值系統,其每個位元可代表的數值並非```1,2,3```而是```-,0,+```,因為其每個位元都可以各自表示負數,因此並不需要特別透過補數或者是前導符號來表示一個負數,不管在於==統一性==、==空間利用效率==甚至是==計算複雜度==上皆有不錯的效果。
本系統最初搭載於1959年,由莫斯科國立大學的一批科學家所設計的實驗電腦 -- Setun,雖然團隊後來在1965年解散,但由於此數值系統的種種優點,後來出現一個名為 Nutes,一個採用本數值系統的 OISC 指令架構電腦,甚至發展出程式語言,展現出了令人驚豔的性能。並且 Nutes 為 Turing-complete,因為其利用本數值系統容易正負轉換的特性,使其可以輕易實作```subtract```、```and```、```branch```、```if```、```negative``` 等被證明可以使用 OISC 指令架構實做的指令。
## 對於 b3k 程式的想法
一開始看到如作業圖中的方塊圖會不知道它在表達什麼,只知道與 3 位元表示法有關,不過多試了幾個範例似乎可以找到一點想法:
```
┌───┐ ┌───┐
┤ │ ┤ │
└┴┴─┘(5) └─┬─┘ (10)
```
只知道凸出爲 + 凹入爲 -,不過試著把 5 跟 10 使用 3 進位組合來表示,得到
$5 = 3^1 + 3^0 + 3^0$ 以及 $10 = 3^2 + 3^0$
10 比較好理解 0 與 2 的邊凸出,但 5 好像不是這麼一回事,有兩個 0 次方的項,因此再改寫爲
$5 = 3^2 - 3^1 - 3^0$
就符合圖中 2 次的邊凸出,而 0 與 1 的邊凹入,因此得到以下原理。
### 原理
Balanced Ternary 能夠使用一個邊長爲 3 單位的正方形來表示數字,從下邊中間爲 3 的 0 次方,依序往左爲 3 的 1 次方到下邊右側爲 3 的 8 次方,而凸出爲加法(或正值),反之凹入爲負值(或減法),若 0 則不變,以下舉個例子說明,假設我們想表示 `100`,做法如下
1. 首先`100`可表示爲 $3^4 + 3^3 - 3^2 + 3^0$
2. 確定每一次項最多只有一項
3. 畫出每次項所代表邊的凹凸
```
├─┴─┐
├ │
└─┬─┘(100)
```
除了圖形的表示法之外,一般使用 `+1,0,-1` 來表示數字,而為了使用上的方便 `-1` 也常使用 `T` 來表示,同樣使用 100 來做例子,由以上改寫 3 次方組合可得知 3 的 0~4 次方係數為 +1,+1,-1,0,+1 因此 100 使用 Balanced Ternary 記為 `11T01`,而表示負數也是一樣,-100可以使用 3 次方表示為
$-100 = -(3^4) - 3^3 + 3^2 - 3^0$
可表示為`TT10T`,與 100 相比較就是差一個負號,因此表示負數也是容易的。
## 理論基礎
### 邏輯操作
既然是數值系統,那當然也必須定義邏輯操作方法。
首先定義真值系統:
| true value | unsigned | balanced |
| -------- | -------- | -------- |
| false | 0 | - |
| unknown | 1 | 0 |
| true | 2 | + |
可以發現,比起二進位系統,其多出了一個惱人的 **unknow** 狀態。
接著是邏輯運算:
AND
| | true | unknown | false |
| ------ | ------- | ------- | ------ |
| true | true | unknown | false |
| unknow | unknown | unknown | false |
| false | false | false | false |
OR
| | true | unknown | false |
| ------ | ------- | ------- | ------- |
| true | true | true | true |
| unknow | true | unknown | unknown |
| false | true | unknown | false |
XOR
| | true | unknown | false |
| ------ | ------- | ------- | ------- |
| true | false | unknown | true |
| unknow | unknown | unknown | unknown |
| false | true | unknown | false |
NOT
| old_value | |
| --------- | ------- |
| true | false |
| unknown | unknown |
| false | true |
從上面表格可以發現 false 在 AND 邏輯中表現相對強勢,OR 邏輯中則是 true 更容易出現,兩者在 XOR 邏輯中平衡,並且依然帶有自反性,另外,NOT 中表現則與與預期相同,比較需要注意的是 NOT unknown 依然是 unknown。
上面表格使用狀態而非數值來表現運算結果,因此可套用於 unsigned 以及 balanced 兩種數值表示方法,並且透過表格讓我們可以更容易理解其數值系統的運算方法。
### 整數
如其他數值系統,最基本的便是表示一個整數,在```Balanced Ternary```當中表示整數的方法同樣可以想成一個式子$a_{0}\times 3^{0} +a_{1}\times 3^{1} + a_{2}\times 3^{2} + ... + a_{i}\times 3^{i} +...+ a_{n}\times 3^{n}$,其中:
* $n$ 為用於給 Balanced Ternary 表示正數的位元數
* $a_{i}$ 為 Balanced Ternary 中第i個位元中的係數
* 只可以是```-1,0,+1```其中之一
* 可表示為```-,0,+```或```T,0,1```
其中若想表示數字時,僅需利用上述數學定義,算出一個係數組合即可。
如:
$4 = 1 + 1\times3^{1}$ => 取其係數得 $11_{bal3}$
$10 = 1 + 0\times3^{1} + 1\times3^{2}$ => 取其係數得$101_{bal3}$
當然也可以輕鬆的表達負整數:
$-10 = -1 + 0\times3^{1} + -1\times3^{2}$ 得 $T0T_{bal3}$
可以發現10與-10的balanced ternary表示方法僅需要將所有係數乘上一個-1即可,十分直覺。
### 小數
有了整數的表示接下來就是小數了,轉換的方法就像大一所學到的相同,必須透過除法。
其式子就像 $a_{-1}\times 3^{-1} + a_{-2}\times 3^{-2} + ... + a_{-i}\times 3^{-i} +...+ a_{-n}\times 3^{-n}$ n與整數部份相同,a~-i~代表各項浮點數係數、n為用於表示小數的位元數。
實際的轉換範例如:
舉$0.3$為例:
```
0.3 => 0.3 * 3 = 0.9 = 1 - 0.1
=> -0.1 * 3 = -0.3 = 0 - 0.3
=> -0.3 * 3 = -0.9 = -1 + 0.1
=> 0.1 * 3 = 0.3 = 0 + 0.3...(loop)
```
因此答案是 $0.\overline{10T0}_{bal3}$。
另外值得注意的是在小數轉換運算上,有時候會發生表示方法並不唯一的狀況,舉$0.5$為例:
```
0.5 => 0.5 * 3 = 1.5 = 1 + 0.5
=> 0.5 * 3 = 1.5 = 1 + 0.5...(loop)
// 然而實際上,我們還有另一種解讀方法。
0.5 => 0.5 * 3 = 1.5 = 2 - 0.5 = 3 - 1 - 0.5 (其中3進位,-1維持原位)
=> -0.5 * 3 = -1.5 = -1 - 0.5
=> -0.5 * 3 = -1.5 = -1 - 0.5...(loop)
```
可以發現上面的解讀方法答案會是$0.\overline{1}_{bal3}$,但若是使用下面的解讀方法就會是$1.\overline{T}_{bal3}$,兩者答案看似並不相同。
然而實際上是如何呢?為了消除疑慮,我們再將答案反推一次。
若將前者轉換回上面提到的式子:
$0.\overline{1}_{bal3} = 0\times3^{0}+1\times3^{-1}+1\times3^{-2}+...+1\times3^{-i}+...$
乍看之下其加總起來似乎不會是$0.5$,但如果稍微做點處理:
令 $a=0.\overline{1}_{bal3}$
=> $\frac{1}{3}_{dec}a=0.0\overline{1}_{bal3}$
=> $a-\frac{1}{3}_{dec}a=\frac{2}{3}_{dec}a=0.1_{bal3}={1\times3^{-1}}_{dec}=\frac{1}{3}_{dec}$
=> $2a=1$
=> $a=0.5_{dec}$
會發現 $a$ 其實是 $0.5$。
接著試著以相同方法處理另一個答案,首先同樣利用上述例子展開。
$1.\overline{T}_{bal3}=1\times3^{0}-1\times3^{-1}-1\times3^{-2}-...-1\times3^{-i}-...$
雖然依然無法得到答案,但這次我們看到了一點線索。
我們發現到小數點後面的部份,乘上-1就會變成$0.\overline{1}_{bal3}$的展開式。
接著很明顯,就是直接使用定義計算:
$1.\overline{T}_{bal3} =1-0.\overline{1}_{bal3}=1-0.5=0.5$
推論過程雖然不算嚴謹,但我們看到的這個數值系統表示小數點以及轉換時所作的事情。
若想避免相同數字轉換出看似不同的balanced ternary,在轉換時可以設定規則,如:可不進位就不進位($0.\overline{1}$),或者是可進位就進位($1.\overline{T}$),避免兩套標準同時存在。
#### 運算邏輯
在進行實際邏輯運算前我們必須定義數個基本邏輯閘,並且在 balanced Ternary 當中,有個十分重要的單元 ternary mutiplexer,其可以作為各式邏輯閘(說的更精確是:[unary function(wikipedia)](https://en.wikipedia.org/wiki/Unary_function))的發展基礎。
接著開始說明:
mutiplexer:
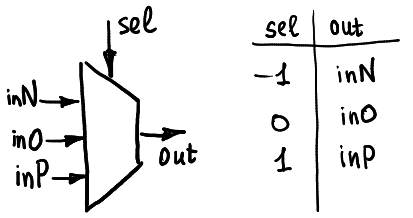
此單元透過改變三個 in 腳位的值,便可以實現各種 unary function,其運作方式是根據 sel 訊號為 -1、0 還是 +1 來決定接通 inN、inO 還是 inP 的訊號。值得注意的是在 ternary 系統中,邏輯單元的 in 腳數會是 3 的倍數,不同於 binary 系統的 2 的倍數。
increase 1:
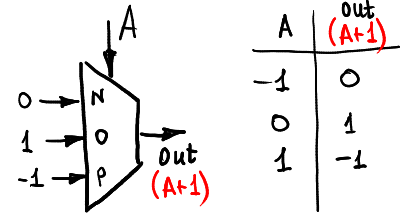
decrease 1:
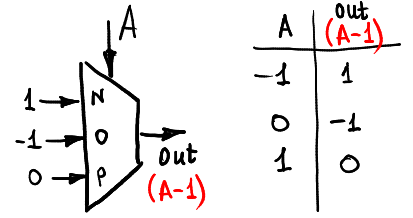
前兩者為位元上的 ```+1``` 及 ```-1``` 操作,可以發現其並沒有包含 carry out 位元。
max(A, 0):
.png)
min(A, 0):
.png)
以上兩者```max(A, 0)```意指挑出 A 與 0 之間比較大的數值,```min(A, 0)```則是挑出較小的。以上四個運算單元將用於推導以下的```half adder```以及```full adder```。
half adder:
首先是 sum:
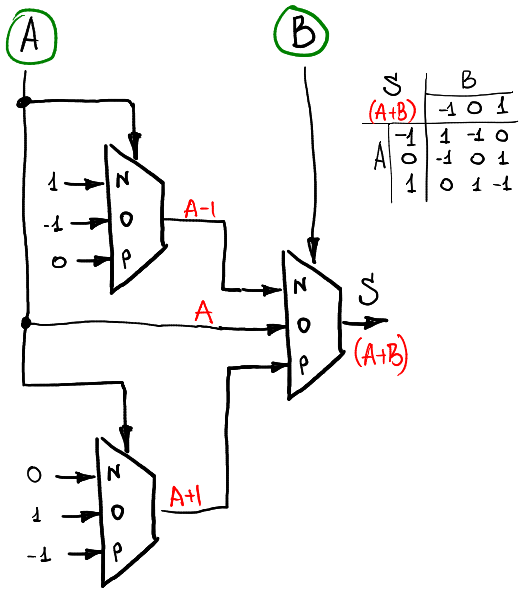
此邏輯僅計算出兩值相加的結果,並未計算進位。為了理解架構,我們將最外層的邏輯轉換成數學式:
$sum(A, B) = A + B =
\begin{cases}
A-1,\ if\ B = -1\\
A,\ if\ B = 0 \\
A+1,\ if\ B = 1
\end{cases}$
便會發現其是符合邏輯的。
接著是 consensus:
.png)
我們同樣從最外層開始轉換:
$consensus(A, B) =
\begin{cases}
min(A, 0),\ if\ B = -1(因若 B=-1,那就不可能有正的進位,只有當A=-1時會進位-1)\\
0,\ if\ B = 0(因若 B=0,不管 A 為何,皆不會有任何進位) \\
max(A, 0),\ if\ B = 1(因若 B=1,除了 A=1 的狀況進位 +1 外,不會有任何進位)
\end{cases}$
透過一些簡單的歸納,便會發現其實這也是合理的,並且了解到若要設計這樣的邏輯,一般來說都會從最高層開始回最低層,甚至使用 [K-MAP(wikipedia)](https://www.wikiwand.com/en/Karnaugh_map) 推導。
full adder:
sum:
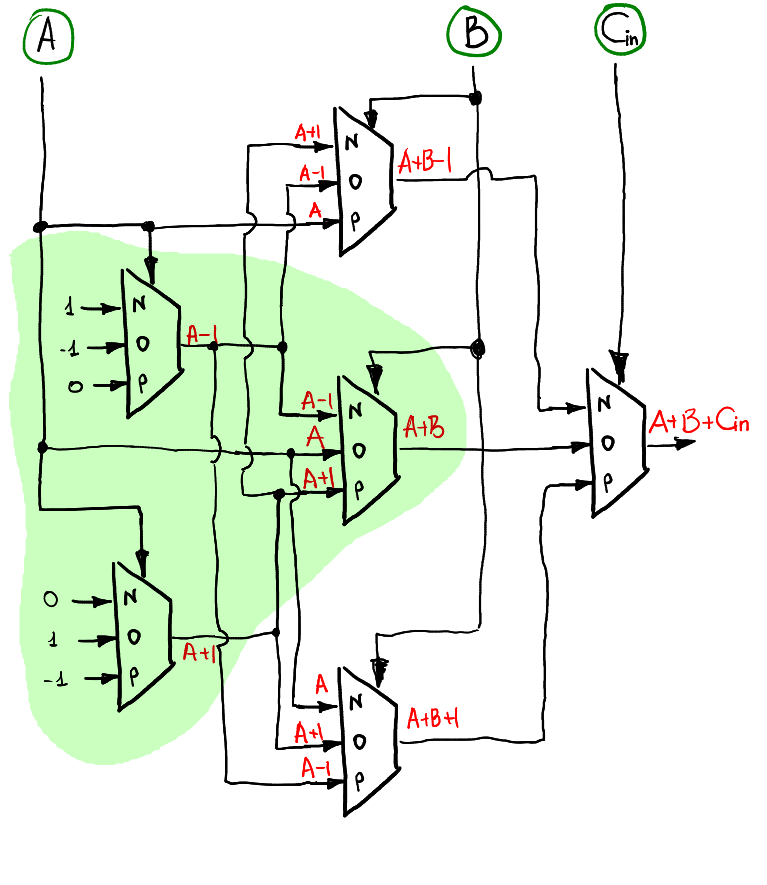
此圖看似複雜,實際上只是將上述兩個SUM半加器結合在一起,若想理解內部運作依然可以透過從頂層推導制底層而得。
overflow:
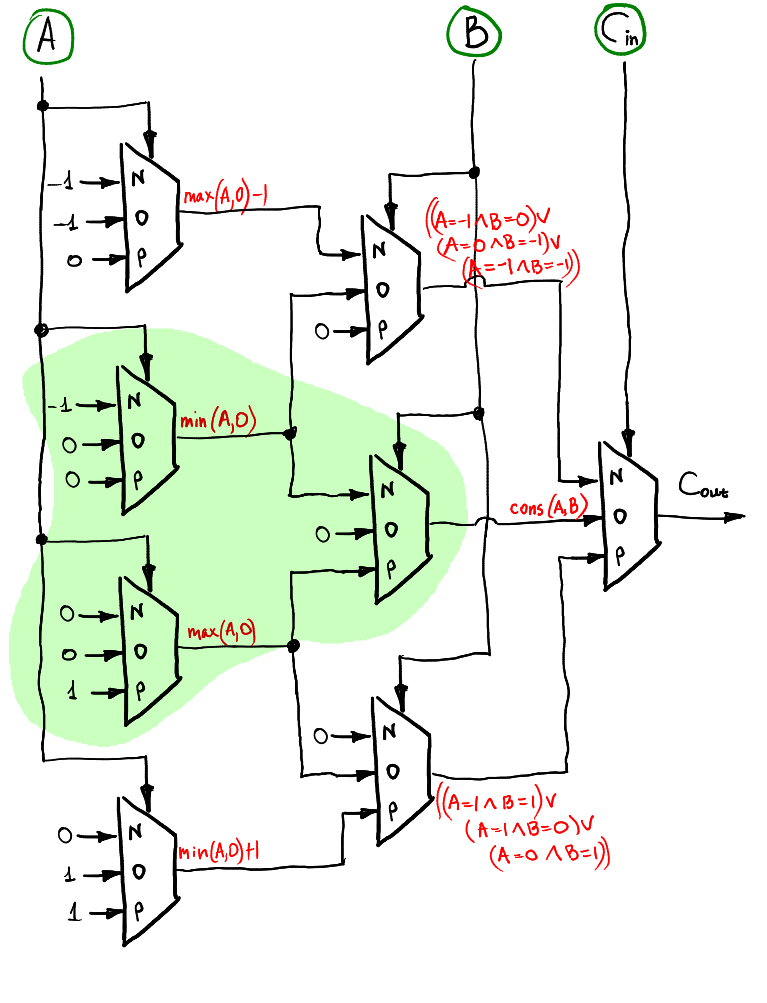
overflow 則是以 consensus 作為基礎,增加一個輸入$C_{in}$來推導電路設計。
至此,我們可以說已經完成了基礎的運算設計,若要需要更複雜的運算則需要以此為基礎繼續進行延伸發展。
> 請閱讀 [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics),關注於 ternary multiplexer, Unary functions, half-adder, Consensus, full adder, Overflow
> [name="jserv][color=blue]
## 與傳統數值系統之比較與測試方法
當然,我們實際上最在意的還是與其他數值系統的比較,這裡我們僅挑選一些常見的數值系統用以比較。
> 繼續研讀 [What is the most efficient numerical base system?](https://math.stackexchange.com/questions/446664/what-is-the-most-efficient-numerical-base-system),並依據裡頭的分析,量化上述討論
> [name="jserv"][color=red]
### 選定之數值系統
這邊我們將選定目前主流電腦系統所採用的 binary (二進位) 與 一般人類常用的 decimal (十進位) 與這裡的 ternary (三進位) ...等系統進行比較。
### 測試與比較方法
關於測試方法,將會以以下三者為討論方向:
* 數值儲存效率 (radix economy)
* 正負轉換效率 (正負數)
* 加法運算效率 (+)
> 不用急著在真實硬體上做實驗,應該先做演算法層級的分析
> [name="jserv"][color=red]
### 演算法比較
首先我們針對演算法層級進行比較,並比較以下兩者:
* 數值儲存效率 (radix economy)
* 正負轉換效率 (正負數)
#### 數值儲存效率
針對數值儲存效率,這邊我們採用 [radix economy](https://www.wikiwand.com/en/Radix_economy) 來進行評估,如下圖:

取自 [radix economy(wikipedia)](https://www.wikiwand.com/en/Radix_economy)
其中 $E(b, N)$ 代表的是一個以 $b$ 為基底的數值系統,在表示常數 $N$ 時需付出的儲存空間代價,可以發現在各數字範圍內以 $e$ 為底的效果皆是最好,另外在 $N$ 為 ```1 to 6``` 以及 ```1 to 43``` 時 $2$ 為基底比 $3$ 為基底的數值系統效率更好。雖然差距微小,難道這就代表 ternary 的儲存效率更差嗎?
為求嚴謹,接著我們就必須使用數學定義來推導出比較公式:
假設我們要比較基底 $b_1$ 及 $b_2$ 時,比較方法可以寫成
$$
\frac{E(b_1, N)}{E(b_2, N)}\approx\frac{b_1\log_{b_1}(N)}{b_2\log_{b_2}(N)}=\frac{(\frac{b_1\ln(N)}{\ln(b_1)})}{(\frac{b_2\ln(N)}{\ln(b_2)})}=\frac{b_1\ln(b_2)}{b_2\ln(b_1)}
$$
可以發現上式去掉了常數 $N$ 的影響,讓我們可以對數值系統進行更全面性的比較。
接著,為了讓此數值可以重用,所有數值系統都可以透過與 $e$ 相互比較,得知其儲存效率。
$$
\frac{E(b)}{E(e)}=\frac{b\ln(e)}{e\ln(b)}=\frac{b}{\ln(b)}
$$
接著再對照上表的 $\frac{E(b)}{E(e)}$ 項目,可以發現除了 $e$,$3$ 的儲存效率是最好的。
#### 正負轉換效率
在這邊我們由於需要計算正負轉換效率,因此針對二進位採用二補數、三進位採用平衡三進位表示負數。
接著我們先舉一個數字```123```為例,在二進位八位元的表示中```123```被表示為```01111011```,平衡三進位八位元則表示為```001TTTT0```,若想將```123```反轉為負數型態,平衡三進位僅須針對所有位元進行反轉,獲得```00T11110```,計算量為 ==8 次位元反轉==。另一方面,二進位計算二補數時得先反轉所有位元後遞增一,獲得```10000100```,計算量為 ==8 次位元反轉加上一次遞增操作==。
若想要量化這份差距,首先我們假設在位元數相同的狀況下,兩者位元反轉所花時間相同,因此差距就主要體現在 +1 的過程中,實際的所花的時間我們以期望值表示,令 $n$ 位元的狀況下,二進位加法的進位次數期望值為 $E(n)$,則 $E(n)$ 可以寫成:
$$
\Sigma_{k=0}^{n-1}((\frac{1}{2})^{k+1}\times k) + (\frac{1}{2})^n\times n
$$
經過繁複的化簡我們可以獲得答案為:
$$
1 - (\frac{1}{2})^n
$$
至此,我們可以說因為二進位轉換時會多進行一次加法,因此轉換效率上平衡三進位將更勝一籌。
### 實作比較
接著我們進行實際的運算,這邊我們僅比較以下運算:
* 加法運算效率 (+)
#### 比較環境
測試時我們採用以下環境:
```
OS: Linux 4.10.0-37-generic x86_64
CPU: Intel(R) Core(TM) i7-6700 CPU @ 3.40GHz
MEMORY: 24GB (DDR4 2133mHz)
COMPILER: gcc 4.9.4 (Ubuntu 4.9.4-2ubuntu1)
```
#### 實作程式
我們在此比較二進位與三進位的加法計算,為求公平我們針對二進位加法與平衡三進位加法各自實作,以下個別解說片段程式碼:
---
實作加法前,我們首先定義各數值系統的基礎位元:
##### binary
```clike=
#define B_FALSE 0
#define B_TRUE 1
typedef uint8_t bit;
```
##### ternary
```clike=
#define T_FALSE 0
#define T_UNK 1
#define T_TRUE 2
typedef uint8_t trit
```
這邊皆是使用 uint8_t 來表示,只是 binary 僅使用一個 bit、 ternary 則使用兩個。
---
接著定義兩者的基礎邏輯閘:
##### binary (AND OR XOR NOT)
```clike=
inline bit B_AND(bit a, bit b) {
bit res = (a == B_TRUE && b == B_TRUE);
return res & B_TRUE;
}
inline bit B_OR(bit a, bit b) {
bit res = (a == B_TRUE || b == B_TRUE);
return res & B_TRUE;
}
inline bit B_XOR(bit a) {
bit res = ((a == B_TRUE && b == B_FALSE) || (a == B_FALSE && b = B_TRUE));
return res & B_TRUE;
}
inline bit B_NOT(bit a) {
return (a == B_FALSE) & B_TRUE;
}
```
##### ternary (MUX)
```clike=
inline trit T_MUX(trit sel, trit inN, trit inO, trit inP) {
trit nf, of, pf;
nf = (sel == T_FALSE);
nf |= nf << 1;
of = (sel == T_UNK);
of |= of << 1;
pf = (sel == T_TRUE);
pf |= pf << 1;
return (nf & inN) | (of & inO) | (pf & inP);
}
```
這邊針對基礎的邏輯運算都使用 inline 前綴來展開,另外相對於 binary 實作了 and、or、xor 以及 not,ternary 只實作了一個多功器(multiplexer),依靠使用時腳位的連接來實現各項功能。
---
接著我們便可以開始定義各自的半加器、全加器以及溢位計算:
##### binary
```clike=
bit B_FA(bit a, bit b, bit cin) {
if (B_XOR(B_XOR(a, b), cin) == B_TRUE) {
return B_TRUE;
} else {
return B_FALSE;
}
}
bit B_OVF(bit a, bit b, bit cin) {
if (B_OR(B_AND(a, b), B_AND(B_XOR(a, b), cin)) == B_TRUE) {
return B_TRUE;
} else {
return B_FALSE;
}
}
```
##### ternary
```clike=
inline trit T_HA(trit a, trit b) {
trit pinN = T_MUX(a, T_TRUE, T_FALSE, T_UNK);
trit pinP = T_MUX(a, T_UNK, T_TRUE, T_FALSE);
trit sum = T_MUX(b, pinN, a, pinP);
return sum;
}
trit T_FA(trit a, trit b) {
return T_HA(T_HA(a, b), cin);
}
trit T_OVF(trit a, trit b, trit cin) {
trit maxCmpZeroDec = T_MUX(a, T_FALSE, T_FALSE, T_UNK);
trit minCmpZero = T_MUX(a, T_FALSE, T_UNK, T_UNK);
trit maxCmpZero = T_MUX(a, T_UNK, T_UNK, T_TRUE);
trit minCmpZeroInc = T_MUX(a, T_UNK, T_TRUE, T_TRUE);
trit inN = T_MUX(b, maxCmpZeroDec, minCmpZero, T_UNK);
trit inO = T_MUX(b, minCmpZero, T_UNK, maxCmpZero);
trit inP = T_MUX(b, T_UNK, maxCmpZero, minCmpZeroInc);
trit ovf = T_MUX(cin, inN, inO, inP);
return ovf;
}
```
binary 的部份由於程式本身的邏輯為二進位,所以可以利用之前定義好的邏輯閘直接組合。相較之下 ternary 則必須定義半加器後才能簡單的定義全加器,並且在於 overflow 尚須花費不少心力撰寫。
---
在實際進入到最終的加法實作前,我們先定義加法的介面:
```clike=
// For binary
int16_t binaryAdd(int16_t a, int16_t b);
// For balanced ternary
uint16_t ternaryAdd(uint16_t a, uint16_t b);
```
兩者皆為有號數加法,只是 binary 直接使用系統原生數值系統並以 ```int16_t``` 儲存,balanced teranry 則使用 ```uint16_t``` 儲存,欲表示一個 trit 至少要有兩個 bit,因此這種儲存方法只能表示到 8trit,兩者使用相同的 bit 數量導致模擬出不同的位元量是希望能盡量貼近現實實作,了解於現行主流電腦架構下兩者的性能比較。
接著,我們定義兩個系統下,取出某個 bit 或者 trit 的方法:
```clike=
bit bitAt(int16_t a, int16_t idx) {
return (bit)((a & (1 << idx)) >> idx);
}
trit tritAt(int16_t a, int16_t idx) {
return (trit)((a & (3 << (idx * 2))) >> (idx * 2));
}
```
另外 ternary 由於並非原生數值系統,輸入輸出時需要經過轉換,這裡亦實作了原生系統與 balanced ternary 互轉以及顯示 balanced ternary 內容的工具:
```clike=
uint16_t decToTer(int16_t a) {
int i, inv = 1;
if (a < 0) {
a *= inv = -1;
}
uint16_t res = 0, carry = 0, remainder;
for (i = 0; i < 8; ++ i) {
remainder = a % 3;
if (remainder + carry == 3) {
carry = 1;
res |= T_UNK << (i * 2);
} else if (remainder + carry == 2) {
carry = 1;
res |= ((inv == 1) ? T_FALSE:T_TRUE) << (i * 2);
} else if (remainder + carry == 1) {
carry = 0;
res |= ((inv == 1) ? T_TRUE:T_FALSE) << (i * 2);
} else if (remainder + carry == 0) {
carry = 0;
res |= T_UNK << (i * 2);
} else {
exit(0)
}
a /= 3;
}
return res;
}
int16_t terToDec(uint16_t a) {
int i, fac;
int16_t res = 0;
for (i = 0, fac = 2; i < 8; ++ i, fac *= 3) {
switch (tritAt(a, i)) {
case T_FALSE: res += -1 * fac; break;
case T_TRUE: res += 1 * fac; break;
}
}
return res;
}
char* showTernary(uint16_t a) {
int i;
char *trit_str = (char*) malloc(sizeof(char) * 8);
for (i = 0; i < 8; ++ i) {
switch (i = 0; i < 8; ++ i) {
case T_FALSE: trit_str[7 - i] = 'T'; break;
case T_UNK: trit_str[7 - i] = '0'; break;
case T_TRUE: trit_str[7 - i] = '1'; break;
}
}
return trit_str;
}
```
---
最後我們便可以開始撰寫加法器邏輯:
##### binary
```clike=
int16_t binaryAdd(int16_t a, int16_t b) {
uint8_t i;
int16_t res = 0;
bit cin = B_FALSE;
for (i = 0; i < 16; ++ i) {
bit ba = bitAt(a, i);
bit bb = bitAt(b, i);
res |= ((uint16_t) B_FA(ba, bb, cin)) << i;
cin = B_OVF(ba, bb, cin);
}
return res;
}
```
##### ternary
```clike=
uint16_t ternaryAdd(uint16_t a, uint16_t b) {
uint8_t i;
uint16_t res = 0;
trit cin = T_UNK;
for (i = 0; i < 8; ++ i) {
trit ta = tritAt(a, i);
trit tb = tritAt(b, i);
res |= ((uint16_t) T_FA(ta, tb, cin)) << (i * 2);
cin = T_OVF(ta, tb, cin);
}
return res;
}
```
兩者使用相同加法邏輯,僅是介面稍有差異。
以上程式碼部份部份參考自 [balanced ternary(github)](https://github.com/sysprog21/balanced-ternary)。
本程式碼維護於 [個人github](https://github.com/FATESAIKOU/Bi-TernaryAdderTest)
:::warning
應該自給定的 GitHub repository 做 fork,集中管理程式碼
:notes: jserv
:::
>好的老師。
>[name=FATESAIKOU]
---
#### 結果
:::info
我們每次測試都會對```binaryAdd```以及```ternaryAdd```進行 -700 至 +699之間的所有數值的所有可能做加法的測試驗證,因此會有 1400 * 1400 種可能,另外本次為了降低程式外因素的影響,運行本測試 1000 次,並配合 ```perf``` 進行效能比較與評估。
:::
以下為程式的執行時間統計結果:
| term\base | binaryAdd | ternaryAdd |
| ---------- | --------- | ---------- |
| time(s) | 861.18451 | 1551.18179 |
發現 ternaryAdd 比 binaryAdd 運行時間將近多了一倍 (1.8012)。
為了探究原因,我們得了解實際上的效能消耗分配,我們在此使用 perf 產生測試程式的紀錄並且解析,結果如下:
| Symbol | Overhead |
| ----------- | ---------- |
| binaryAdd | 5.01% |
| bitAt | 5.27% |
| B_FA | 2.74% |
| B_OVF | 3.78% |
| B_AND | 3.34% |
| B_OR | 1.71% |
| B_XOR | 11.23% |
| ==BINARY== | ==33.08%== |
| ternaryAdd | 2.22% |
| tritAt | 4.34% |
| T_FA | 1.28% |
| T_OVF | 4.89% |
| T_HA | 4.96% |
| T_MUX | 44.01% |
| ==TERNARY== | ==61.70%== |
| (Total) | 94.78% |
:::info
這裡移除了測時程式中無關加法的部份(e.g. 數值轉換),並且由於兩者加法測試為一口氣執行,因此表中的比例為相對於==測試程式整體的效能消耗比例==。其中 ==BINARY== 與 ==TERNARY== 所指為 binary 與 ternary 兩者的效能消耗加總,Total 則為將前兩者加總之結果。
:::
我們發現兩者加法效能消耗差距依然很大,但同時也發現到, Ternary 加法運算中其基礎運算的時間消耗非常高,達到整體執行時間的 ==44%== 。接著我們看看實際編譯出來的組合語言,了解其效能消耗的緣由:
:::info
左側為指令在於函式整體的效能消耗,右側為實際指令,同時亦適時插入被編譯的程式碼片段幫助思考 [編譯對照參考來源](https://godbolt.org/g/wywAiy)
:::
```clike=
// trit T_MUX(trit sel, trit inN, trit inO, trit inP) {
1.98 │ push %rbp
2.09 │ mov %rsp,%rbp
1.93 │ mov %ecx,%eax
1.46 │ mov %dil,-0x14(%rbp)
2.15 │ mov %sil,-0x18(%rbp)
1.48 │ mov %dl,-0x1c(%rbp)
0.55 │ mov %al,-0x20(%rbp)
// nf = (sel == T_FALSE);
1.48 │ cmpb $0x0,-0x14(%rbp)
3.08 │ sete %al
1.68 │ mov %al,-0x3(%rbp)
// nf |= nf << 1;
1.59 │ movzbl -0x3(%rbp),%eax
2.71 │ add %eax,%eax
3.35 │ mov %eax,%edx
0.45 │ movzbl -0x3(%rbp),%eax
0.78 │ or %edx,%eax
2.57 │ mov %al,-0x3(%rbp)
// of = (sel == T_UNK);
4.90 │ cmpb $0x1,-0x14(%rbp)
0.50 │ sete %al
0.44 │ mov %al,-0x2(%rbp)
// of |= of << 1;
2.73 │ movzbl -0x2(%rbp),%eax
4.68 │ add %eax,%eax
2.18 │ mov %eax,%edx
0.38 │ movzbl -0x2(%rbp),%eax
1.23 │ or %edx,%eax
3.57 │ mov %al,-0x2(%rbp)
// pf = (sel == T_FALSE)
4.44 │ cmpb $0x2,-0x14(%rbp)
0.30 │ sete %al
1.01 │ mov %al,-0x1(%rbp)
// pf |= pf << 1;
3.78 │ movzbl -0x1(%rbp),%eax
5.55 │ add %eax,%eax
3.11 │ mov %eax,%edx
0.79 │ movzbl -0x1(%rbp),%eax
1.32 │ or %edx,%eax
3.33 │ mov %al,-0x1(%rbp)
// return (nf & inN) | (of & inO) | (pf & inP)
6.71 │ movzbl -0x3(%rbp),%eax
0.69 │ and -0x18(%rbp),%al
1.00 │ mov %eax,%edx
0.32 │ movzbl -0x2(%rbp),%eax
3.51 │ and -0x1c(%rbp),%al
0.70 │ or %eax,%edx
1.03 │ movzbl -0x1(%rbp),%eax
3.45 │ and -0x20(%rbp),%al
3.80 │ or %edx,%eax
// <End Function Call>
4.57 │ pop %rbp
0.67 │ ← retq
```
可以發現,消耗還算平均並且指令奇長無比,其中雖耗時最長的為 movzbl ,但透過重新編譯並測試另外一個版本(但並不正確)的 T_MUX 發現其應為引用到外部輸入參數時不可避免的記憶體讀取消耗。
因此在此我們暫時扣除雙方的基礎邏輯消耗,單純就兩者的半加全加器以及溢位偵測來進行比較。結果發現雙方消耗變得十分接近(binary: 16.8%, ternary: 17.69%)。
至此我們可以說 Ternary 加法實做效率上,若能在多功器(Multiplexer) 上有更高的硬體支援性,或者更好的軟體效能調校,其可以是有機會接近原生的 Binary 計算的。
> 在比較其他數值系統時,應當考慮到 balanced ternary 的 adder (全加器), half-adder (半加器) 一類實作。參考: https://github.com/ternary-info/ternary-logisim/tree/master/screenshots (從邏輯電路回推設計)
> [name="jserv"][color=red]
## Balanced Ternary 可以用來解決什麼問題
綜合以上報告,我們總結出幾項重點:
### 儲存空間利用效率高,但實際應用時必須妥協。
:::info
如 ==[前述](#數值儲存效率)== ,數值儲存效率上除去 $e$ 後,便是 ternary 效率最高,但必須特別注意的是二進位在於數值範圍較小的時候(1 ~ 43、1 ~ 182)其表現非但較差,甚至可能超越 ternary ,加上 ternary 在二進位系統上實作時依然必須透過原生的 bit 來進行模擬,導致 ternary 數值系統的儲存效率優勢主要表現在更大的數值空間中。當然應用時也可以透過一些壓縮方法使得不必使用兩個 bit 來代表每一個 trit,但相對來說也將付出更大的效能損耗。
:::
### 數值運算理論上快,但於主流二進位架構上模擬時將伴隨效能損耗。
:::info
如 ==[實作比較](#實作比較)== 所述,雖然三進位以及二進位加法器皆使用漣漪進位加法器作為基本設計,但由於所運行的電腦系統架構屬於二進位邏輯不同於三進位,導致其加法器在最基礎的多功器上消耗了非常多的時間,==[比對](#結果)== 下來三進位加法器比二進位版本將近多了一倍的運算時間。因此在實際應用時,還是得深入思考如何加速運算時間以及降低計算次數。
:::
### 正負數儲存表現對稱,轉換效率高於二進位,但轉換小數可能產生重複性。
:::info
由於平衡三進位本身儲存特性,其表示正負數時僅為相互的位元完全反轉,不如現行二進位系統位元反轉後依然需要透過加法進行補數操作。但正式因為其具備這樣的對稱性,因此在轉換其他數值空間的某個數值時將有可能出現兩個答案(詳見:==[小數](#小數)==),因此實際應用時為避免誤判必須確保數值來自相同一套轉換邏輯。
:::
根據以上我們可以大致了解到 Ternary 數值系統置於現代主要具備了==儲存效率==、==精確==以及==轉換==方面的優勢,特別針對對於==較大數據==的儲存要求特別苛刻並且同時要求其==精準度==的場景。但要特別注意的是這樣的數值系統應用於傳統二進位架構下時並非完全沒有缺點,若要對其進行運算我們必須犧牲部份的運算能力,其所伴隨的便可能是耗電量或者成本。
而實際上已經有這套數值系統的應用案例--[IOTA](https://iota.org/)
### 實際應用案例 IOTA
IOTA 是個針對物連網應用而生的機器與機器之間的加密貨幣系統,其中底層採用了 Balanced Ternary 作為其數值系統,希望可以透過此方法降低儲存帳本時所消耗的空間,並同時提昇精度,對於其小額交易時所需儲存的長浮點數來說可謂一大福音。
#### 交易發起流程
若要在 IOTA 中發起一個交易,則必須依序執行以下步驟:
1. 選擇兩個交易並驗證 (允許兩筆交易是相同的)。
2. 檢查兩這筆交易是否衝突,並且這個衝突是否並未被驗證過。
3. 使交易合法化 (若交易衝突則僅合法一個)
4. 發出交易
#### 交易新增儲存與權重
IOTA 用於儲存交易紀錄的方式不同於區塊鏈,其是透過一個稱為 Tangle 的有向不成環圖所構成 (DAG),詳如下圖:

取自 [Tangle 中文白皮書](https://hackmd.io/c/rkpoORY4W/https%3A%2F%2Fhackmd.io%2Fs%2FB1YKzhbLb%23)
如圖中所示,可以發現網路中每個交易皆指向兩個其他交易,印證在新增交易時如[上面](#交易發起流程)所述,將會指向 (驗證) 兩個其他交易,接著才新增交易。另外,圖中每個交易的右下角表示其==自身權重==,左上角則是指==累積權重==,兩者與交易選擇的演算法(tip selection)有關,其中自身權重為交易產生時其自身所帶有的權重,累積權重則是自身權重以及所有==驗證過這個交易的節點的權重==之和。
特別注意,驗證時只能挑選==未被驗證==過的交易 (即未被任何交易指向),因此上圖在增加交易 $X$ 時,只能選擇 $A、B、C$ 三者之二 (可重複) 來進行驗證。而可用於選取、未被驗證的交易我們將其稱為 tip。
#### 交易驗證方法
對於比特幣等傳統虛擬貨幣為了利用區塊鏈來儲存交易紀錄,使用高難度、高複雜度的數學題目來挑選符合資格的"礦工"來認證及經手交易(因此需要支付手續費,並且導致一部分的中心化)。
但在於 Tangle 網路當中則不存在這類的礦工,取而代之的是發起交易時本身需要付出計算效能驗證兩個交易紀錄,但實際上由於網路本身不需要"提高"驗證交易的成本,因此計算效能相較區塊鏈也低得非常多,以此達到==完全去中心化==的共識(驗證)方法,同時也不需要支付手續費。
#### 為何採用 Balanced Ternary
對於其理論上的高運算效能、高儲存效能以及高轉換效率,Iota 設計者認為其為於物聯網應用虛擬貨幣的不二數值系統,透過此的確可以降低物聯網節點在儲存交易上的成本,並且配合更容易執行的共識演算法可以避免消耗大量算力。
但實際上 Iota 在應用上依然必須解決大量的實務應用問題(eg.: 於二進位系統上儲存與運算),關於這方面社群中其實依然存在不少[反論](https://hackernoon.com/why-i-find-iota-deeply-alarming-934f1908194b),當然也同時存在著正向的討論,這也正說明 IOTA 是一份新的嘗試,透過重複地提出問題並且解決不斷地接近目標。
#### 與 Balanced Ternary 之相關性與程式碼片段
首先我們可以看到 IOTA 使用了 Balanced Ternary 來表示 hash 的結果:
```clike=
tryte_table = {
'9': [ 0, 0, 0], # 0
'A': [ 1, 0, 0], # 1
'B': [-1, 1, 0], # 2
'C': [ 0, 1, 0], # 3
'D': [ 1, 1, 0], # 4
'E': [-1, -1, 1], # 5
'F': [ 0, -1, 1], # 6
'G': [ 1, -1, 1], # 7
'H': [-1, 0, 1], # 8
'I': [ 0, 0, 1], # 9
'J': [ 1, 0, 1], # 10
'K': [-1, 1, 1], # 11
'L': [ 0, 1, 1], # 12
'M': [ 1, 1, 1], # 13
'N': [-1, -1, -1], # -13
'O': [ 0, -1, -1], # -12
'P': [ 1, -1, -1], # -11
'Q': [-1, 0, -1], # -10
'R': [ 0, 0, -1], # -9
'S': [ 1, 0, -1], # -8
'T': [-1, 1, -1], # -7
'U': [ 0, 1, -1], # -6
'V': [ 1, 1, -1], # -5
'W': [-1, -1, 0], # -4
'X': [ 0, -1, 0], # -3
'Y': [ 1, -1, 0], # -2
'Z': [-1, 0, 0], # -1
}
```
參考 [HMKRL 共筆](https://hackmd.io/s/rJGc0TmiZ),取自 [iotaledger/kerl(Github)](https://github.com/iotaledger/kerl/blob/7ca94d3e8bc7b8223fe10e25c853b01273735968/python3/conv.py)
接著是實際將 binary 數值轉換為 Balanced Ternary 的片段:
```clike=
// All possible tryte values
var trytesAlphabet = "9ABCDEFGHIJKLMNOPQRSTUVWXYZ"
// map of all trits representations
var trytesTrits = [
[ 0, 0, 0],
[ 1, 0, 0],
[-1, 1, 0],
[ 0, 1, 0],
[ 1, 1, 0],
[-1, -1, 1],
[ 0, -1, 1],
[ 1, -1, 1],
[-1, 0, 1],
[ 0, 0, 1],
[ 1, 0, 1],
[-1, 1, 1],
[ 0, 1, 1],
[ 1, 1, 1],
[-1, -1, -1],
[ 0, -1, -1],
[ 1, -1, -1],
[-1, 0, -1],
[ 0, 0, -1],
[ 1, 0, -1],
[-1, 1, -1],
[ 0, 1, -1],
[ 1, 1, -1],
[-1, -1, 0],
[ 0, -1, 0],
[ 1, -1, 0],
[-1, 0, 0]
];
/**
* Converts trytes into trits
*
* @method trits
* @param {String|Int} input Tryte value to be converted. Can either be string or int
* @param {Array} state (optional) state to be modified
* @returns {Array} trits
**/
var trits = function( input, state ) {
var trits = state || [];
if (Number.isInteger(input)) {
var absoluteValue = input < 0 ? -input : input;
while (absoluteValue > 0) {
var remainder = absoluteValue % 3;
absoluteValue = Math.floor(absoluteValue / 3);
if (remainder > 1) {
remainder = -1;
absoluteValue++;
}
trits[trits.length] = remainder;
}
if (input < 0) {
for (var i = 0; i < trits.length; i++) {
trits[i] = -trits[i];
}
}
} else {
for (var i = 0; i < input.length; i++) {
var index = trytesAlphabet.indexOf(input.charAt(i));
trits[i * 3] = trytesTrits[index][0];
trits[i * 3 + 1] = trytesTrits[index][1];
trits[i * 3 + 2] = trytesTrits[index][2];
}
}
return trits;
}
```
參考 [st9007a共筆](https://hackmd.io/s/rJv_CTmsb)
可以發現上面這份程式碼使用了同樣一個轉換表,並且實作了轉換程式於下方。
## 參考專案與文獻
* [balanced ternary(Github)](https://github.com/sysprog21/balanced-ternary)
* [Balanced Ternary(Wikipedia)](https://www.wikiwand.com/en/Balanced_ternary)
* [平衡三进制(baidu)](https://baike.baidu.com/item/%E5%B9%B3%E8%A1%A1%E4%B8%89%E8%BF%9B%E5%88%B6#1_3)
* [Balanced Ternary半/全加器(Github)](https://github.com/ternary-info/ternary-logisim/tree/master)
* [yoelmatveyev/nutes(Github)](https://github.com/yoelmatveyev/nutes/tree/master)
* [st9007a共筆](https://hackmd.io/s/rJv_CTmsb)
* [HMKRL共筆](https://hackmd.io/s/rJGc0TmiZ)
* [c2 wiki](http://wiki.c2.com/?ThreeValuedLogic)
* [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)
* [Ternary computer(Wikipedia)](https://www.wikiwand.com/en/Ternary_computer)
* [unary function(Wikipedia)](https://en.wikipedia.org/wiki/Unary_function)
* [K-MAP(Wikipedia)](https://www.wikiwand.com/en/Karnaugh_map)
* [Radix economy(Wikipedia)](https://www.wikiwand.com/en/Radix_economy)
* [IOTA](https://iota.org/)
* [iotaledger/kerl(Github)](https://github.com/iotaledger/kerl)
* [Tangle 中文白皮書](https://hackmd.io/c/rkpoORY4W/https%3A%2F%2Fhackmd.io%2Fs%2FB1YKzhbLb%23)
* [Bi-TernaryAdderTest(FATESAIKOU github)](https://github.com/FATESAIKOU/Bi-TernaryAdderTest)
* [Why I find Iota deeply alarming(Hacknoon)](https://hackernoon.com/why-i-find-iota-deeply-alarming-934f1908194b)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet