# 2017q3 Homework1 (ternary)
contributed by <`ian910297`>

### Reviewed by `jcyztw`
* 作業區的 github 連結請修正為此份作業的 github repository 連結，目前的連結會連到 Homework1 作業區頁面。
* 如同老師在作業區的批閱評語，還有很多[作業要求](https://hackmd.io/s/Sym0UAk9Z#%E4%BD%9C%E6%A5%AD%E8%A6%81%E6%B1%82)尚未完成，有空的話趕快補上吧。(P.S. 我自己也還有很多要求沒做完，一起加油吧！)

## TODO
* 實驗設計
* 案例觀察

## Balanced Ternary

> TODO: 詳細閱讀 [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)，理解 base-3 的原理 (並且複習數位邏輯)，整理 base-3 基礎運算操作
> [name="jserv"][color=red]

這是一個不需要正負號，就能表示正負數的數值系統，由三個符號組成`T,0,1`
`T` 表示 $-1$
`0` 表示 $0$
`1` 表示 $1$

### 整數
將其表示成十進位的數學式
$\sum\limits_{i=1}^{n}a_{i} \times 3^{i-1}$
$a_{i} \in {T, 0, 1}$
* $n$ 表示有幾位數
* $i-1$ 表示從零次方開始

舉例說明
$10T_{bal3}$
$\to n = 3$
$\to -1 \times 3^0 + 0 \times 3^1 + 1 \times 3^2$
$\to 6$

### 小數

## 運算
### ternary multiplexer
下圖電路設計，有 5 個 pin 腳`(sel, inN, inO, inP, out)`，表示會根據 selector 對應的三種狀態`(N, O, P)`輸出對應的值`(inN, inO, inP)`
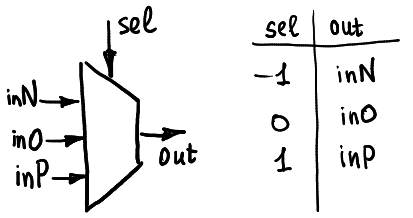
>英文、數字與中文間請以空白隔開
>[name=課程助教][color=red]
>
### unary functions
文中提到四種基本的單元，走馬看花即可，只是定義稍後會用到的基本單元
* $A+1$
* $A-1$
* $max(A,0)$
* $min(A,0)$
### half-adder
以 half-adder 為例，推導過程。須先畫出真值表，並由後往前推導
已知 $S'$ 為 $A+B$
* $B=-1$，A必須是 $(1, -1, 0)$
* $B=0$，A必須是 $(-1, 0, 1)$
* $B=1$，A必須是 $(0, 1, -1)$

只從真值表裡我們看不出這三個單元有什麼意義，但已知結果是$A+B$，那當 $B=-1$ 帶入就可以直接將其`inN`解讀為 $A-1$，同理可帶入值去解釋另外兩個輸入的意義
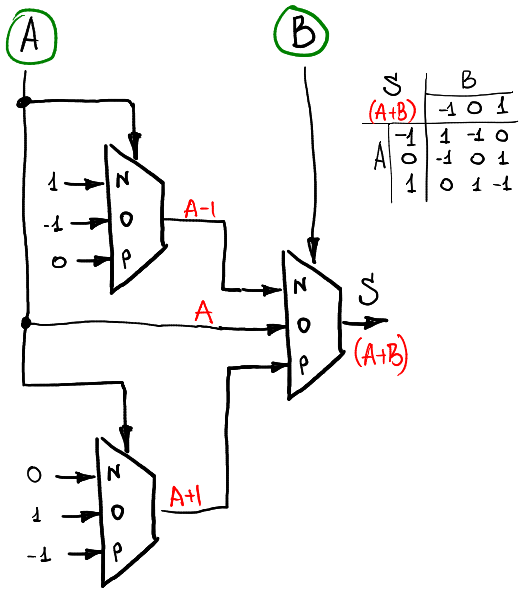
### Overflow
由於 consensus 與 fulladder，跟 half-adder 推倒過程相像，不再說明
這邊與前三者最大的不同在於複雜度，需要先列出可能的狀況，再寫出真值表輔助
比如說下圖在計算當$C_{in}=-1$，`inN`的輸入單元為何，先列出可能的狀況，在畫出真值表，即可湊數

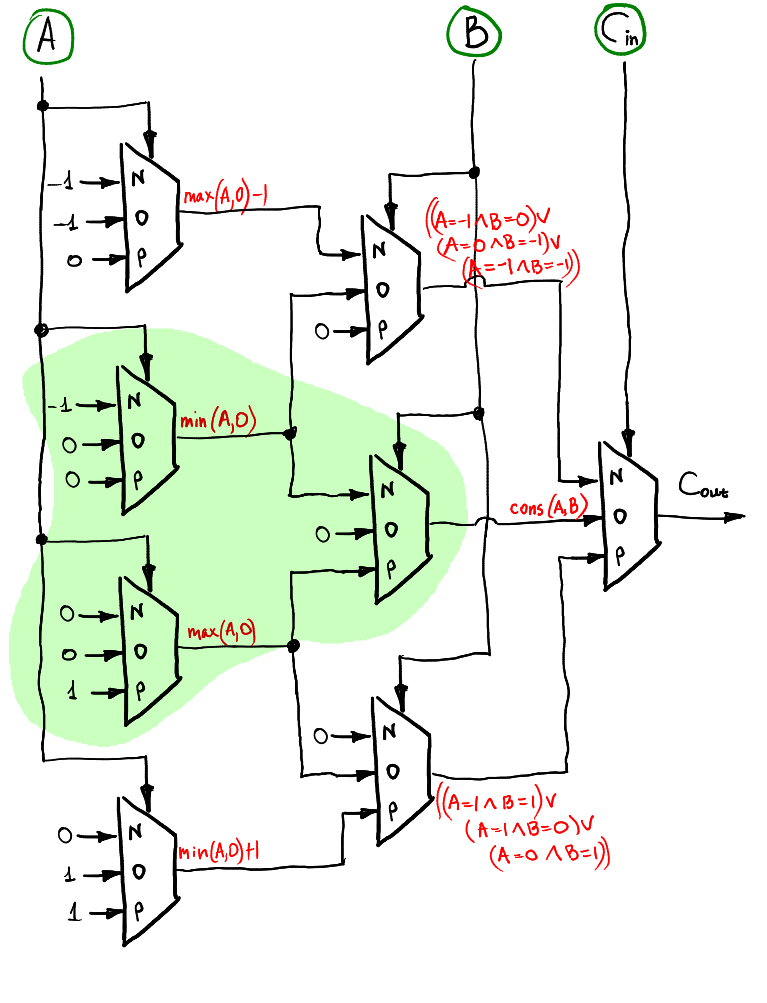
> 請閱讀 [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)，關注於 ternary multiplexer, Unary functions, half-adder, Consensus, full adder, Overflow
> [name="jserv][color=blue]

## 參考文獻
* [Wikipedia: Balanced Ternary](https://en.wikipedia.org/wiki/Balanced_ternary)
> "wiki" 是可供多人協同創作的超文本系統，而 Wikipedia 是運用 wiki 技術和概念而建構的線上百科全書，這兩者不同，所以你不能把 Wikipedia 簡稱 "wiki"
> [name="jserv"][color=red]

## IOTA 案例分析
- [ ] 閱讀 [IOTA 繁體中文白皮書](https://hackmd.io/c/rkpoORY4W/https%3A%2F%2Fhackmd.io%2Fs%2FryriSgvAW)