# Leetcode刷題學習筆記 -- Selection, Insertion, Bubble, Heap
## Time Complexity
### Comparison-based sorting technique
| | Best | Average | Worst | Space | stability |
| -------------- | ---------- | ---------- | ------------ | --------- | --- |
| Selection Sort | $O(N^2)$ | $O(N^2)$ | $O(N^2)$ | $O(1)$ | non-stable |
| Bubble Sort | $O(N)$ | $O(N^2)$ | $O(N^2)$ | $O(1)$ | stable |
| Insertion Sort | $O(N)$ | $O(N^2)$ | $O(N^2)$ | $O(1)$ | stable |
| Heap Sort | $O(NlogN)$ | $O(NlogN)$ | $O(NlogN)$ | $O(1)$ |non-stable |
## Reference
+ [Selection Sort Algorithm](https://www.geeksforgeeks.org/selection-sort/?ref=lbp)
+ [Bubble Sort Algorithm](https://www.geeksforgeeks.org/bubble-sort/?ref=lbp)
+ [Insertion Sort](https://www.geeksforgeeks.org/insertion-sort/?ref=lbp)
+ [Heap Sort](https://www.geeksforgeeks.org/heap-sort/?ref=lbp)

## Stable Sorting
+ ==When two same data appear in the same order in sorted data without changing their position is called stable sort.==
+ Example: merge sort, insertion sort, bubble sort.

## Selection(Max/min value) Sort
每次都選擇從後面看到的最大或最小值來和目前的位置替換。就可以達到排序的效果。

 void SelectionSort(vector<int>& nums) {
    int sz = nums.size();
    for(int i = 0; i < sz - 1; ++i) { // 從第一個位置開始
        int minidx = i; 
        // 找尋 i之後的最小值
        for(int j = i + 1; j < sz; ++j) {
            if(nums[j] < nums[minidx]) {
                minidx = j;
            }
        }
        // 將結果交換過來
        if(i != minidx)
            swap(nums[i], nums[minidx]);
    }
 }

因為沒有break的機制，即使是排序過的數列，也是要$O(N^2)$
## Bubble Sort
只和相鄰比較，把較大或較小的數值往右移動。

void BubbleSort(vector<int>& nums) {
    int sz = nums.size();
    for(int i = 0; i < sz - 1; ++i) {
        for(int j = 0; i < sz - j - 1; ++j) {
            if(nums[j] > nums[j + 1]) 
                swap(nums[j], nums[j + 1]);
        }
    }
}

## Insertion (to right position) sort
假設前面已經排列完成，下一個element就不斷地交換直到正確的位置為止。
使用swap是因為避免使用insert會有O(N)的time complexity。

void InsertionSort(vector<int>& nums) {
    int sz = nums.size();
    for(int i = 1; i < sz; ++i) {
        int j = i;
        while(j >= 1 && nums[j] < nums[j - 1]) {
            swap(nums[j], nums[j - 1]);
            j--;
        }
    }
}

## Heap sort
+ ==in-place== algorithm
+ Its typical implementation is ==not stable==, **but can be made stable**.

### Advantages of heapsort
+ Efficiency - time complexity $O(NlogN)$
+ Memory Usage - $O(1)$, no additional memory space to work
+ Simplicity - 簡單理解實現。

### Applications of HeapSort
+ 使用在混合的sort algorithm，像是IntroSort。
+ [Sort a nearly sorted (or K sorted) array](https://www.geeksforgeeks.org/nearly-sorted-algorithm/)
+ [k largest(or smallest) elements in an array](https://www.geeksforgeeks.org/k-largestor-smallest-elements-in-an-array/)

### Heapify
把其中一個非leaf的node中，將極值(最大或最小)一直往leaf推的過程。
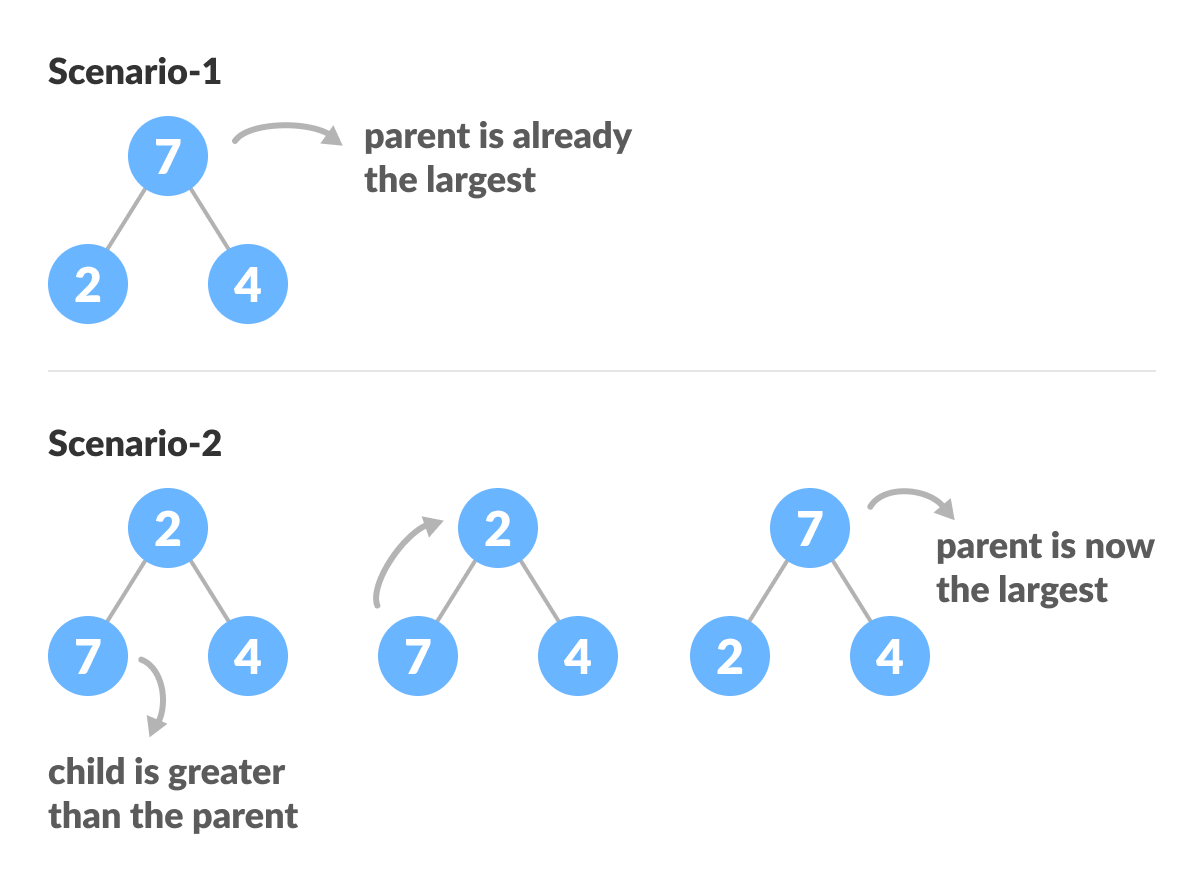
例如scenario-2中，因為left child(7)比root(2)還大，所以交換這兩個值。
當全部的非leaf node都走訪過一次後，最大值就會出現在root。

### Steps of heap sort
以max heap為例:
1. build max heap(parent一定會大於等於child)
2. 經過第一步之後最大值會在root, index = 0的位置。
3. 把最大值移到最後的位置。
4. 再做一次heapify，
5. 回到step2

### Sample code of heap sort

// To heapify a subtree rooted with node i
// which is an index in arr[].
// n is size of heap
void heapify(vector<int>& arr, int sz, int i)
{
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int maxidx = i;
    
    // 找出最大數值的index
    if(left < sz && arr[maxidx] < arr[left])
        maxidx = left;
    if(right < sz && arr[maxidx] < arr[right])
        maxidx = right;
    
    // 如果最大數值不是root
    if(maxidx != i) {
        swap(arr[i], arr[maxidx]);
        // Recursively heapify the affected sub-tree
        heapify(arr, sz, maxidx);
    }
}
 
// Main function to do heap sort
void heapSort(vector<int>& arr, int sz)
{
    // 1. Build heap (rearrange array)
    for(int i = sz / 2 - 1; i >= 0; --i)
        heapify(arr, sz, i);

    // One by one extract an element from heap
    for(int i = sz - 1; i >= 0; --i) {
        //3. Move current root to end
        // 因為build heap之後最大值會在idx = 0
        swap(arr[0], arr[i]);
        //4. call max heapify on the reduced heap
        // 因為idx = 0 數值改變了
        heapify(arr, i, 0); 
    }
}

###### tags: `leetcode` `刷題`