---
tags: vaje, or, grafi
hackmd: https://hackmd.io/hXNa6YldToSiGGZB8Vj2kg
plugins: mathjax, mermaid
---
# Operacijske raziskave - vaje 4.5.2020
---
## Iskanje v širino
```python
class Graf:
...
def BFS(G, visit=None, koreni=None):
globina = {}
stars = {}
if visit is None:
def visit(u, v):
pass
if koreni is None:
koreni = G.vozlisca()
for w in koreni:
if w in globina:
continue
nivo = [w]
globina[w] = 0
stars[w] = None
i = 1
while len(nivo) > 0:
naslednji = []
for u in nivo:
visit(u, stars[u])
for v in G.sosedi(u):
if v not in globina:
globina[v] = i
stars[v] = u
naslednji.append(v)
nivo = naslednji
i += 1
for u in G.vozlisca():
if u not in globina:
globina[u] = float('inf')
stars[u] = None
return (globina, stars)
```
Časovna zahtevnost: $O(m) + O(n)$ klicev funkcije `visit`
---
### Naloga 1
Na sledečem grafu izvedi iskanje v širino. V primerih, ko imaš več enakovrednih izbir, upoštevaj abecedni vrstni red. Za vsako povezavo določi, ali se nahaja v drevesu iskanja v širino.
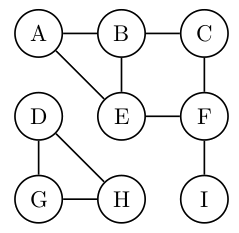
----
| | A | B | C | D | E | F | G | H | I |
| ------- | - | - | - | - | - | - | - | - | - |
| globina | 0 | 1 | 2 | 0 | 1 | 2 | 1 | 1 | 3 |
| stars | / | A | B | / | A | E | D | D | F |
0. nivo: A
1. nivo: B, E
2. nivo: C, F
3. nivo: I
----
0. nivo: D
1. nivo: G, H
```mermaid
graph TD
A --- B
A --- E
B --- C
E --- F
F --- I
D --- G
D --- H
```
---
### Naloga 2
Zapiši algoritem, ki za vhodni graf <i>$G$</i> določi njegov premer.
----
```python
class Graf:
...
def premer(G):
return max(x for u in G.vozlisca()
for x in G.BFS(koreni=[u])[0].values())
```
Časovna zahtevnost: $O(mn)$
---
## Dijkstrov algoritem
```python
class UtezenDigraf(Digraf):
...
def utezeniSosedi(G, u):
"""
Vrne slovar uteži povezav
od u do vsakega njegovega soseda.
"""
...
def dijkstra(G, koren):
Q = PrednostnaVrsta({v: 0 if v == koren
else float('inf')
for v in G.vozlisca()})
razdalja = {}
stars = {koren: None}
while len(Q) > 0:
v, d = Q.pop() # vozlišče z najmanjšo razdaljo v vrsti odstranimo iz vrste
razdalje[v] = d
for w, t in G.utezeniSosedi(v).items():
if w in razdalje:
continue
r = d + t
if r < Q[w]:
Q[w] = r
stars[w] = v
return (razdalje, stars)
```
Časovna zahtevnost:
* s slovarjem: $O(n^2)$
* s kopico: $O(m \log n)$
Kopica:
```mermaid
graph TD
0 --- 1
0 --- 2
1 --- 3
1 --- 10
2 --- 5
2 --- 7
3 --- 6
3 --- 8
```
---
### Naloga 3
S pomočjo Dijkstrovega algoritma določi razdalje od vozlišča <i>$A$</i> do ostalih vozlišč.
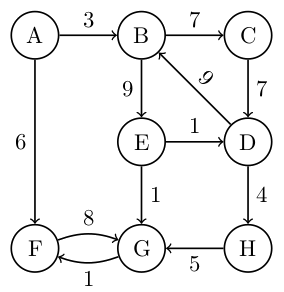
----
| | A | B | C | D | E | F | G | H |
| -------- | - | - | -- | -- | -- | - | -- | -- |
| vrsta | | | | | | | | |
| razdalja | 0 | 3 | 10 | 13 | 12 | 6 | 13 | 17 |
| stars | / | A | B | E | B | A | E | D |
```mermaid
graph TD
A -- 3 --> B
A -- 6 --> F
B -- 7 --> C
B -- 9 --> E
E -- 1 --> D
E -- 1 --> G
D -- 4 --> H
```
---
### Naloga 4
Naj bo $G = (V, E)$ graf, za katerega so dolžine povezav določene s funkcijo $\ell : E \to \mathbb{R}$ (tj., dolžine so lahko tudi negativne). Definirajmo še funkcijo $\ell' : E \to \mathbb{R}$ tako, da velja $\ell'(e) = \ell(e) - \min\{\ell(f) \mid f \in E\}$ (dolžine, določene z $\ell'$, so torej nenegativne).
Dokaži ali ovrzi: drevo najkrajših poti, ki ga Dijkstrov algoritem ustvari ob vhodu $(G, \ell')$, je tudi drevo najkrajših poti za graf <i>$G$</i> z dolžinami povezav, določenimi z $\ell$.
----
```mermaid
graph LR
A == 2 ==> B
A -- 1 --> C
B == -3 ==> C
```
```mermaid
graph LR
A -- 5 --> B
A == 4 ==> C
B -- 0 --> C
```
---
### Naloga 5
Denimo, da imamo neusmerjen graf $G = (V, E)$, katerega vozlišča predstavljajo mesta, povezave pa predstavljajo ceste, ki jih povezujejo. Za vsako povezavo $e \in E$ poznamo njeno dolžino $\ell_e$ (v kilometrih).
Priti želimo iz mesta <i>$s$</i> v mesto <i>$t$</i>. V vsakem mestu je bencinska črpalka, ob cestah pa teh ni. Žal imamo na voljo samo star avto, ki lahko s polnim rezervoarjem prepelje le <i>$L$</i> kilometrov.
1. Zapiši algoritem, ki v linearnem času poišče pot, ki jo lahko prevozimo z našim avtom, oziroma ugotovi, da ta ne obstaja.
2. Izkaže se, da z našim avtom te poti ne moremo prevoziti, zato se odločimo za nakup novega. Zapiši algoritem, ki v času $O(m \log n)$ določi najmanjše število prevoženih kilometrov, ki naj jih avto zmore z enim polnjenjem, da bo pot od <i>$s$</i> do <i>$t$</i> mogoča.
---
### Naloga 6
Zasnuj različico Dijkstrovega algoritma za iskanje najkrajše poti med vozliščema <i>$s$</i> in <i>$t$</i> v grafu <i>$G$</i>, ki iskanje hkrati začne v vozliščih <i>$s$</i> in <i>$t$</i>. Kdaj naj se iskanje konča in kako naj se poišče rešitev?
 Sign in with Wallet
Sign in with Wallet

