# Tornado Cash
## 有限域
使用原因:
计算机内存有限,无法表示任意精度。
比如:
使用`node`和`python`计算10除以3结果为`3.3333333333333335`。
现阶段即使最可靠的语言也会放弃任意精度。
我们实现一个新的数字系统,他将实现一下目的:
- 只使用整数(0、1、2、3、4、5、、、、n-1)
- 没有无限多的数字,只有一组有限数字,计算结果也在这些有限数字(域)内。
- 所有现有的算数计算方式新的数字系统也支持(加减乘除等)
基础:模运算
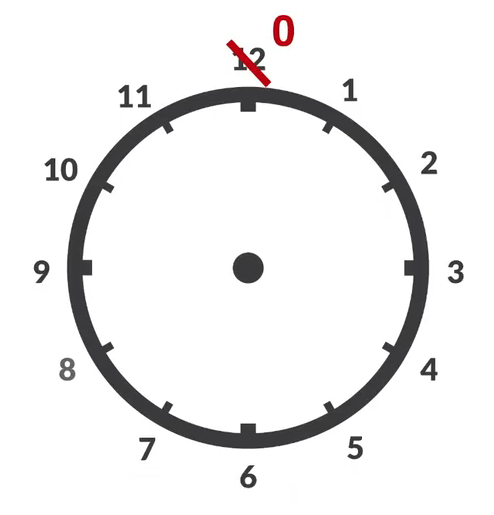
质数域(有限域)
| Topic | Features |
| -------- | ------------------------------------------------------------ |
| 元素 | 1> `0 `至 `p-1`的数字组成 |
| 加法 | 2> 使用模元算来定义 <br />3> 单位元素是`0`或者顶部数字`p`<br />4> 加法逆元被定义成相加等于`0`的一对数字,这个概念取代了负数,也取代了减法 |
| 乘法 | 5> 乘法计算也遵循模运算<br />6> 乘法的单位元素是 `1`<br />7> 乘法逆元被定义为一对互补数字,当它们相乘时产生单位元素`1`,这个概念取代了除法 |
| 指数运算 | 8> 来自连续乘法,乘法在质数域中良好定义,通过指数运算扩展,可得出指数运算在质数域中良好定义<br />9> 定义生成元,生成元时集合内的原始元素,若连续对其进行指数运算,将生成有限集内的每一个其它元素,并有一个重要属性:生成元的`p-1`次方的结果总是为 `1` |
```
设定/特点:
- 顶部元素(`12/0`)为加法的单位元,或者零元,因为任意数字相加都得到数字本身,同理1为乘法的单位元。
- 负数为相加起来等于零的互补数对,我们称其为加法逆元,而不是负数,使用逆的概念取代负数的概念。
- 加法逆元为一对互补数字,加起来等于`0`。
- 任何两个数字,如果相乘的到乘法单位元(1),则称他们为互为乘法逆元。
- 使用的有限集为`0`至 `n-1`,`n`为时钟顶部的位置,即`0`。
- 加法使用模运算来定义,以便将大的求和结果带回到域本身。
- 加法单位元是零元素`n`,即放在时钟顶部的单位。
- 有限集合的元素与顶部数字不共享任何除数(我们可以简单的选择一个质数作为时钟顶部元素,否则就会出现模运算结果无法覆盖有限集所有元素的情况,如顶部元素为12时,3的n次方的模运算只有几个特定值)。
- 除以`0`依旧未定义。
```
此图的加法逆元表:
| n | Inverse n |
| :--: | :-------: |
| 1 | 11 |
| 2 | 10 |
| 3 | 9 |
| 4 | 8 |
| 5 | 7 |
| 6 | 6 |
| 7 | 5 |
| 8 | 4 |
| 9 | 3 |
| 10 | 2 |
| 11 | 1 |
模加法示例:
3-11 = 3+(-11) = 3+1 = 4
模乘法示例:
7 * 2 = 14 = 12 * 2 + 2 = 2
5 * 6 = 30 = 12 * 2 + 6 = 6
10 * 12 = 120 = 12 * 10 + 0 = 0
如果选择一个质数放在时钟顶部,我们称之为质数域。一个质数域的完整乘法表(p = 7):
| Mu l | 1 | 2 | 3 | 4 | 5 | 6 | 7/0 |
| :--: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 0 |
| 2 | 2 | 4 | 6 | 1 | 3 | 5 | 0 |
| 3 | 3 | 6 | 2 | 5 | 1 | 4 | 0 |
| 4 | 4 | 1 | 5 | 2 | 6 | 3 | 0 |
| 5 | 5 | 3 | 1 | 6 | 4 | 2 | 0 |
| 6 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 7/0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
可以看到结果中包含了有限域中和的所有元素,没有出现循环行为。
乘法逆元示例:
2 / 3 = 2 * (3^-1) = 2 * 5 = 3
指数运算:
| Pow. | Equivalent | Pro. | Modular | Result |
| :--: | --------------------- | ---- | ----------- | ------ |
| 3^1 | 3 | 3 | 7 * 0 + 3 | 3 |
| 3^2 | 3 * 3 | 9 | 7 * 1 + 2 | 2 |
| 3^3 | 3 * 3 * 3 | 27 | 7 * 2 + 6 | 6 |
| 3^4 | 3 * 3 * 3 * 3 | 81 | 7 * 11 + 4 | 4 |
| 3^4 | 3 * 3 * 3 * 3 * 3 | 243 | 7 * 34 + 5 | 5 |
| 3^6 | 3 * 3 * 3 * 3 * 3 * 3 | 729 | 7 * 104 + 1 | 1 |
可以看到元素3在质数域中不会出现循环情况。每提升一个次方,就会产生其他每一个元素,最终会到达集合内的其它元素。这种元素行为使其成为一个生成元/原始元素。其特点是如果连续对其进行指数运算,它将生成整个集合。
**生成元的一个重要属性:成元的`p-1`次方的结果总是为 `1`。**
## 离散对数问题
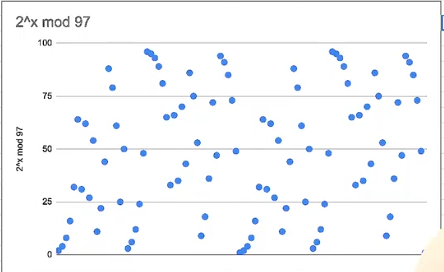
对指数做模运算后会发现结果很不好预测。(对数是指数的逆运算)
**离散对数问题的结论:在有限域内解对数非常困难。**
当你在有限域内对同一个元素进行多次乘法操作时,它隐藏了相乘的次数。(注意此性质,它对隐藏`x`解很重要)
## 零知识证明简介
零知识证明的一些基本要素:
1. 需要一个单独的设置和互动规则。
2. 在验证着和证明者之间,验证者会向证明者提出挑战问题。
3. 在设置阶段预先定义挑战的问题,与证明者拥有的不可观察的真相的特点特征、功能、函数、独特特征等相关。
4. 验证需要有终止条件,要么接受要么拒绝。其中证明者的有效答案将触发验证者接受证明者的声明,即他确实拥有符合给定标准的信息,答案不正确则拒绝接受。
5. 这个系统总是会有不确定元素,零知识证明系统的结论永远不会是100%正确的。
## 零知识证明数学案例分析
以 某人拥有
$$
x^2 + 4x + 7 = 0
$$
的解 为例(在模997内寻找解):
设:
$$
V(I) = 300^I
$$
这是一个简单的指数函数,并且300是质数域997的生成元。
这样设置有两个原因:
- 生成元的`p-1`次方的结果总是为 `1`
- 如果`I = p-1`,则
$$
v(I) = 300^{p-1} = 1
$$
因为`p`为顶部元素,即零元,则:
$$
v(I) = 300^{x^2+4x+7-1} = 300^{x^2+4x+6} = 1
$$
至此我们将原有的证明声明转换成了一个新的证明声明,然后把根据新的验证设置函数。
为什么要这样做呢?
当你用模运算符家在末尾将求和分解成单独项时,就会将模运算分解到每个单独项中。
$$
v(I) = 300^{x^2+4x+6} = 300^{x^2 mod 997} * 300 ^{4x mod 997} * 300^6
$$
而当你在有限域内对同一个元素进行多次乘法操作时,它隐藏了相乘的次数,即隐藏了 `x^2`、`4x`。而`x`恰好是我们想要隐藏的。
这样,现在证明者可以发送`x`的编码版本(`300^x^2`、`300^4x`),等效代替原始证明,就可以说明证明者可能确实知道满足原始方程的`x`。
所以,验证设置如下:
1. 有一个单独的验证设置
$$
V(I) = 300^I
$$
2. 采用哪种挑战问题
要求证明者发送A(=300^x^2), B(= 300^4x)
3. 接受标准,一个决定是否接受证明者声明的标准
验证者验证 A * B * 300^6 = 1,则测试通过。
## circom中的基本算术电路
circom:将复杂的数学方程简化为简单的电路运算来描述数学过程。
- 在生产验证系统中,有效的证明不仅需要输入值,还需要所有的中间值来构建。这提高了伪造证明的难度。
- 扩展性。Groth是一种一次性设置的验证系统,一旦有了问题的电路描述,那么完成验证设置就像将一个数字插入到一个函数那么简单。只要插入电路,就为你生成一个验证系统。但是需要一种非常通用的方式来描述这些商业活动或者数学运算。circom是一个很好的选择,因为它只使用加法和乘法门。
- 信号,包括输入,所有中间值,所有见证人和输出。我们需要描述每个门之间的数量关系的方程。如:
$$
f(x,y) = x^2y+xy^2+17
$$
信号表示为:
```
x * x = m1
m1 * y = m2
y * y = m3
x * m3 = m4
o = m2 + m4 + 17
```
在信号方程中,最多只有一次信号之间的乘法。
这实际就是用于生成验证系统的方程系统,被称为一阶约束系统,即`R1CS`,描述了电路内数量之间的关系。
**一个demo**
circom、snarkjs安装:https://docs.circom.io/getting-started/installation/#installing-circom
```shell
创建项目:
npm init -y
安装依赖:
npm install --save circom snarkjs
新建文件:
touch circom.circom
```
```js
pragma circom 2.0.0;
// f(x,y) = x^2 * y + x * y^2 + 17
// Signal Definition:
// 1、所有的输入都是信号
// 2、每次将两个信号相乘时,都需要定义一个新的信号
// 3、一次只能占用两个信号来获取一个新的信号
// 4、所有的输出都是信号
// 模版
template F() {
// Declaration of signals.
signal input x;
signal input y;
signal output o;
signal m1 <== x * x;
signal m2 <== m1 * y;
signal m3 <== y * y;
signal m4 <== m3 * x;
o <== m2 + m4 + 17;
}
//组装
component main = F();
```
编译电路:
```
将其编译成 R1CS 和 WebAssembly:
circom circom.circom --r1cs --wasm
```
运行电路:
```
input.json:
{
"x": 2,
"y":3
}
生成见证:
node ./circom_js/generate_witness.js ./circom_js/circom.wasm input.json witness.wtns
```
就会生成一个代表所有见证的二进制文件。如果要读取的话需要将其转成j s:
```
snarkjs wtns export json witness.wtns witness.json
witness.json:
[
"1",
"47",
"2",
"3",
"4",
"12",
"9"
]
```
见证文件的第一个数字总是`1`,代表电路中的常量操作。接下来时总输出`47`,然后是两个输入`2`、`3`,剩下的是全部的中间变量。
## MIMC 哈希电路
MIMC含义:最小乘法复杂度。
哈希函数的实现方式:
$$
F(x) = (x + k + g)^3
$$
当输入常量K和G,然后进行幂运算,操作越多次,越能掩盖原始数字。这就是它为什么会输出一个哈希。这是一个不可逆函数,所有哈希函数都是如此。
随机常量在 MIMC 初始化时选择有限域中的随机元素,然后固定下来。这意味着当实现 MIMC 哈希函数时,需要为每轮的加密生成一堆常量,然后硬编码到代码中,无论对什么做哈希,它们都会保持不变。
哈希函数电路实现:
```js
pragma circom 2.0.0;
template MIMC5() {
// Declaration of signals.
signal input x;
signal input k;
signal output h;
var nRounds = 10;
var c[nRounds] = [
0,
18306687113883968518773305135814488358176083808813054563815085114441907421609,
28775042267900106674004003818311383890356920779197943873558139717867667301403,
10646004036085173582161772598322508733033235722142696401677275812451383218426,
79386406729580134365639080545738781721728472515692126537259957703398136088192,
62242654296843257469589256646358677564706947459511971583298897633042897307430,
100757216228217238239007064371612967739349752303491399624903885788260695209128,
507509826840708981343713881905337579016630481226461005569912286517617204348,
84151666979564219931596845972660527041047222493679972951736475653661048649949,
63371771133525813111661365558608359052049356932502237121489308974094194458244
];
signal lastOutput[nRounds + 1];
var base[nRounds];
signal base2[nRounds];
signal base4[nRounds];
lastOutput[0] <== x;
for (var i = 0; i < nRounds; i++){
base[i] = lastOutput[i] + k + c[i];
base2[i] <== base[i] * base[i];
base4[i] <== base2[i] * base2[i];
lastOutput[i+1] <== base4[i] * base[i];
}
}
component main = MIMC5();
```
生成`bignumber`实现:
```js
const { ethers } = require("ethers");
const num = 10;
async function generate() {
for (let i = 0; i < num; i++) {
// uint256 256/8 = 32
let n = ethers.BigNumber.from(ethers.utils.randomBytes(32));
console.log(n.toString());
}
}
generate().catch((err) => { console.log(err); process.exit(1); });
```
"ethers": "^5.6.0"
```
编译:
circom circuit.circom --r1cs --wasm
创建见证:
touch input.js
{
"x": "12345678901234567890123456789012345678901234",
"k": "76543210987654321098765432109876543210987654"
}
node ./circuit_js/generate_witness.js ./circuit_js/circuit.wasm input.json output.wtns
将生成的见证转换为json可读形式:
snarkjs wtns export json output.wtns output.json
```
## 算数电路中的 Groth16 设置
Groth16是一种验证设置系统。
两个问题:
- 输入(包括所有见证值)经历了什么样的转变
- 有什么替代的证明陈述
系统工作:
- 纯文本输入,这些输入包含你拥有的秘密信息、所有见证值,这些值都没有进行编码,处于原始状态,任何人获取到这些信息都会知道秘密
- 经过第一步转换,变成`R1CS`,展平了电路,并且在这个过程中所有见证值在一个系统方程力清晰整齐地排列好,将所有的幂运算都转化了,并且只包含加法和乘法。
- 第二步转换变成了`QAP`二次算术程序,是一个巨大的多项式,可以编码大范围数字、操作、约束、数字之间的关系。这对见证值的编码非常有用。尤其是已经将原数据转化为一个简单的系统方程,像`R1CS`。最终的编码中多项式`F(x)`包含非常高的次数(上千次方算小的)。
- 转换了所有的输入、见证值,并将它们编码在多项式中,怎么知道他们是正确的呢?可以将它与一个预期多项式来比较。如:`G(x)`是电路的预期行为,如果经过正确的执行和预期的编码`F(x)`和1`G(x)`应该拥有相同的多项式。当然不能逐个比较,那样会暴露多项式构造。你需要通过将评估值映射到到椭圆曲线`(bn128)`上的点来评估它们。
- 是哪个关键步骤让整个系统运作起来呢?就是多项式比较。如果相同,那么就接受证明者声称的原始输入是有效的。如何比较呢?最简单的的就是逐个比较每一项,但是效率会非常低,不仅需要大量运算,还会暴露内部结构,即多项式本身的系数和幂次。我们可以在一组随机点上评估两个多项式是否相同。如果在随机选定的点上始终评估为相同的值,那么我们就得出这两个多项式是相同的结论。但是这么做需要保证点的随机性,否则有人就有可能根据测试点伪造多项式。这就是`Groth16`需要一个可信设置的原因。
- 可信设置涉及大量的参与者,所有人都会决定多项式会在哪些点上进行评估,称之为熵。在这个随机性的贡献过程中,如果至少一个参与者完全保密,则整个可信设置将成功并保证`Groth16`设置的安全性。
***Groth16的程序设置***
1. 通过仪式创建一个可信设置,`Groth16`的这个仪式称之为`powers of Tau`,使用bn128曲线创建一个新的仪式。将这个仪式文件对象传递给大量第三方,他们都将为这个仪式对象贡献额外的随机性,具体数字是随机的。这些随机值之后需要被删除。
2. 要使用这个仪式文件为特定的电路设置验证设置,你需要以某种方式将它们交织在一起,在第二阶段设置特定方式。首先获得最终的仪式文件,然后将它与想设置的电路交织在一起,获取到一个`zkey`文件,这将是你的证明密钥,每次想为特定电路生成证明时都会需要它。
3. 生成证明,需要电路、电流执行的输入`json`和`ZKey`文件
我们以完成的`MIMC5`哈希电路为例进行`Groth16`设置:
1、创建一个仪式文件
```
snarkjs powersoftau new bn128 12 ceremoy_0000.ptau -v
```
12代表最大约束数。当我们编译电路时,会给你一个输出,详细说明电路有多少约束。12代表电路可以拥有的最大约束数是`2^12`。
最后命名为`ceremoy_0000.ptau`,将数字附加到仪式词的末尾是传统做法,这样就可以跟踪哪些参与者为这个仪式文件贡献了随机性。
2、为这个仪式文件贡献随机性
在现实生活中,你会将这个生成文件传递给其他人,他们将它们选择的随机性贡献给仪式文件,你不应该知道其他参与者的贡献。贡献之后这些数字和输入应该被丢弃,因为我们只需要最后的生成文件。
```
snarkjs powersoftau contribute ceremoy_0000.ptau ceremoy_0001.ptau -v
```
输入随机数或者文字完成后,删除` ceremoy_0000.ptau`,继续提供随机性
```
snarkjs powersoftau contribute ceremoy_0001.ptau ceremoy_0002.ptau -v
```
..........
从别人那里获取到仪式文件时可以验证完整性,因为你需要确保为该文件贡献随机性之前,仪式文件没有以任何方式被破坏。
验证仪式文件完整性:
```
snarkjs powersoftau verify ceremoy_0002.ptau
```
若最后一行打印出`[INFO] snarkJS: Powers of Tau Ok!`,则意味着仪式文件正确。
当文件随机性贡献完成后,生成最终文件:
```
snarkjs powersoftau prepare phase2 ceremoy_0002.ptau ceremoy_final.ptau -v
```
它将计算用来测试多项式的一组随机挑战。
验证最后的生成文件:
```
snarkjs powersoftau verify ceremoy_final.ptau
```
3、使用`Groth16`设置,将生成文件与电路交织在一起
首先,编译电路成`R1CS`,我们就可以给它提供仪式文件:
```
circom circuit.circom --r1cs
```
生成密钥:
```
snarkjs groth16 setup circuit.r1cs ceremoy_final.ptau setup_0000.zkey
```
这个`ZKey`文件可以之间使用,但是不建议,我们为这个`ZKey`文件贡献一次额外的随机性。
```
snarkjs zkey contribute setup_0000.zkey setup_final.zkey
```
验证最后的`ZKey`文件:
```
snarkjs zkey verify circuit.r1cs ceremoy_final.ptau setup_final.zkey
```
4、生成`Proof`
先添加输入元素`json`文件:
```
{
"x": "12345678901234567890123456789012345678901234",
"k": "76543210987654321098765432109876543210987654"
}
```
先将电路编译成`web assembly`形式:
```
circom circuit.circom --wasm
```
生成`Proof`:
```
snarkjs groth16 fullprove input.json circuit_js/circuit.wasm setup_final.zkey proof.json public.json
```
根据`ZKey`文件和验证密钥生成一个验证器合约:
```
snarkjs zkey export solidityverifier setup_final.zkey Verifier.sol
```
生成验证字符串:
```
snarkjs zkey export soliditycalldata public.json proof.json
```
然后就可以在合约中验证。
这样,我们已经知道如何实现一个电路,然后设置一个对那个电路的零知识证明验证系统。
## 通读 `Tornado Cash`白皮书
合约部分推荐文档:
https://www.rareskills.io/zh/post/tornado-cash%E5%B7%A5%E4%BD%9C%E5%8E%9F%E7%90%86%EF%BC%88%E9%9D%A2%E5%AF%B9%E5%BC%80%E5%8F%91%E4%BA%BA%E5%91%98%E7%9A%84%E9%80%90%E8%A1%8C%E8%A7%A3%E6%9E%90%EF%BC%89
https://www.rareskills.io/post/how-does-tornado-cash-work
规划:
整个项目由两部分组成:前端和合约,合约的总体围绕着默克尔树操作。
前端:
存款人存入时需要:一个`K`值和秘密,这两个都是256位的。然后会计算一个承诺哈希,是`K`与秘密链接后的`Patterson`哈希,然后调用存款函数,带上哈希和ETH,合约将其放入一个空的叶子结点。这些最后都会作为一个事件发出,这样存款人就可以拥有这些信息,将它们提供给取款人,以构建证明。
取款:
取款构建证明需要知道`K`,秘密和当时存款生成的`ROOT`根植,一组姐妹节点的值,一个接收者地址。然后计算`Proof`,最后可以顺利提款。提款后合约会记录相关的证明哈希到已花费的零知识证明哈希中,这个证明就不能再取ETH了。
## 自己实现
我自己基于Tornado官方的core代码实现的自己的Tornadocash-core(电路2.0.0版本):
https://github.com/CornersOfTheCity/tornadocash-core
参考文档:
https://www.rareskills.io/zh/post/tornado-cash%E5%B7%A5%E4%BD%9C%E5%8E%9F%E7%90%86%EF%BC%88%E9%9D%A2%E5%AF%B9%E5%BC%80%E5%8F%91%E4%BA%BA%E5%91%98%E7%9A%84%E9%80%90%E8%A1%8C%E8%A7%A3%E6%9E%90%EF%BC%89
https://www.rareskills.io/post/how-does-tornado-cash-work
https://www.cnblogs.com/ACaiGarden/p/18182834
使用 zkSNARK 在以太坊上进行匿名投票:
https://foresightnews.pro/article/detail/47366
 Sign in with Wallet
Sign in with Wallet

