# <div id=animation_title>排序法與時間複雜度</div>
###### tags: `C++`

**<a href="https://hackmd.io/CSZ3EUqhSRa8AyDyBMq1Bw" class="redlink">點此回到 C++筆記 目錄 </a>**

## <span class="purple">時間複雜度 O</span>
> **1. 大 O 符號是用來描述一個演算法在輸入 n 個東西時，總執行次數與 n 的關係。**
> **2. 演算法有多快不是以秒衡量，而是以步驟次數**
> **3. 紀錄最高次方的那一項，並忽略其所有的係數**

## 常見的時間複雜度與演算法
### 1. O(1)

char arr[8] = {'a','b','c','d','e','f','g','h'};

假設我們已經知道這個陣列裡面全部的元素與順序，那當我們想找到"d"時，我們只要輸入n=3就可以找到它了

cin >> n;
cout << arr[n] << endl;

由上面的例子我們能發現，無論n輸入了多少，執行次數都是1次，因此時間複雜度為 O(1)

</br>

### 2. O(n)
這邊我們沿用上方的陣列

char arr[8] = {'a','b','c','d','e','f','g','h'};

假設我們現在只知道這個陣列裡面有abcdefgh，但不知道順序，那麼如果我們想找到"d"，要怎麼辦呢?

最簡單的方法就是一個一個找(線性搜尋法)，從第一個找到第八個，如果找到了就停止。

for(i=0 ; i < sizeof(arr)/sizeof(arr[0]) ; i++ ){

    if(arr[i] == 'd') {

       cout << i << endl;       
       break;
   }
}

輸出: 3

我們可以發現在最糟的情況下，要搜尋的次數會等於的陣列長度(n)，因此時間複雜度為 O(n)

<br>

### 3. O(logn) —— 二分搜尋法
假設今天我們要從1~99裡猜一個數字，除了上方的線性搜尋法，有沒有什麼更好的方法呢?

有的，這就是我們接下來要談的二分搜尋法。 同時，說到O(logn)，最經典的例子便是它。

那麼什麼是二分搜尋法呢? 步驟如下:

1.檢查上界與下屆中間的數字i
2.如果大於目標，便把下界設為i。反之，如果小於目標，就把上界設為i
3.回到步驟一

<a href="https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E5%BE%9E%E6%99%82%E9%96%93%E8%A4%87%E9%9B%9C%E5%BA%A6%E8%AA%8D%E8%AD%98%E5%B8%B8%E8%A6%8B%E6%BC%94%E7%AE%97%E6%B3%95-%E4%B8%80-b46fece65ba5"><center><img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_2a72ed5fed623c1a8d354cf52cd2e61b.png" width="600"></center></a>

我們可以把它寫得更清楚，如下

1. 決定好左邊界 L，右邊界 R
2. 取 M = (L+R)/2，作為中間的 index
3. 如果 array[M] == 要找的數，return M
4. 如果 array[M]>要找的數，表示 M~R 這一段數字都是不可能的，所以讓 R = M - 1
5. 如果 array[M]<要找的數，表示 L~M 這一段數字都是不可能的，所以讓 L = M + 1
6. 如果 R>=L，持續第 2 步，否則回傳 -1（代表找不到）

<a href="https://blog.techbridge.cc/2016/09/24/binary-search-introduction/"><center><img src="https://static.coderbridge.com/img/techbridge/images/huli/binary_search.gif"></center></a>

這邊的停止條件是「當L>R」的時候，就代表找不到了
因為 L 代表：最左邊的有可能的值。換句話說，假如有答案，一定在 >=L 的位置
R 代表的是：最右邊有可能的值，假如有答案，一定在 <=R 的位置
所以當L > R 的時候，>=L 跟 <=R 已經是空集合了，代表不可能有答案

首先我們先宣告變數並建一個陣列，如下

    int n;          //陣列大小(1~數字n)
    int i;          //迭代器
    int target;     //目標數(array[M] == target)

    cout << "n =";
    cin >> n;
    int arr[n]={0};

    int L = 0;                                  //下界
    int R = sizeof(arr)/sizeof(*arr)-1;         //上界
    int M;                                      //猜target在第幾個

    cout << "target= ";
    cin >> target;

    for(i=0; i < n; i++){

        arr[i] = i+1;

    }
    

現在我們有一個陣列了，假設我們輸入n=99，target=76，代表我們建了一個陣列，裡面有數字1~99，然後我們想要找到76在陣列中的index是多少 ( 陣列: [1, 2, 3, ... , 97, 98, 99] )

那麼現在要開始用二分演算法來找到76的index了，如下

while(R >= L) {

        M = (int)(L + R)/2;
        //cout << "L = " << L << endl << "R = " << R << endl << "M = " << M << endl << "arr[M] = " << arr[M] << endl << endl;

        if(arr[M] > target) {

            R = M-1;

        }

        else if(arr[M] < target) {

            L = M+1;

        }

        else if(arr[M] == target) {

            cout << M;
            break;

        }
    }


輸入: n=99, target=76
輸出: 75

可以把註解打開，看看L M R是如何變化的。
經過一些數學運算，我們能發現執行的次數約為logn次 (n為陣列大小，也可以說是輸入的資料數)，因此時間複雜度為 O(logn)

二分法還有些其他的狀況，有興趣可以到<a href="https://blog.techbridge.cc/2016/09/24/binary-search-introduction/">這裡</a>看看

<br>

### 4-1. O(n²) —— 選擇排序法(Selection Sort)
假設今天我們有一個未排序的數字陣列，那我們要將它由小排到大，可以怎麼做呢? 解決這個問題的方法就是我們接下來要討論的排序法。

第一種方法是選擇排序法，這個排序法非常簡單，簡單來說只有兩個步驟，如下
1. 從「尚未排序的數字」中找最小值
2. 把這個最小值丟到「未排序數字」的最左邊

不停地重複這兩個動作，直到沒有未排序的數字，這就是選擇排序法!

假設現在有一個未排序的陣列[41, 33, 17, 80, 61, 5, 55]，那麼排序的情況會如下圖
<center><a href="https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E6%8E%92%E5%BA%8F%E6%B3%95%E5%85%A5%E9%96%80-%E9%81%B8%E6%93%87%E6%8E%92%E5%BA%8F%E8%88%87%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F%E6%B3%95-23d4bc7085ff"><img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_70bca464eb96df6e2010fe04e618fbeb.png"></a></center><br>

首先我們先宣告變數並建一個陣列，如下

    int i;
    int j;
    int min_index;
    int a;

    int arr[] = {41, 33, 17, 80, 61, 5, 55};

這樣我們就有一個未排序的陣列了，現在要開始用選擇排序法來排序，如下

for(i = 0; i < sizeof(arr)/sizeof(*arr); i++ ) {

        min_index = i;

        for(j = i+1; j < sizeof(arr)/sizeof(*arr) ; j++) {

            if(arr[j] < arr[min_index]) {

                min_index = j;
            }
        }
        
        //cout << "arr[i] = " << arr[i] << " arr[min_index] = " << arr[min_index] << endl;
        a = arr[i];
        arr[i] = arr[min_index];
        arr[min_index] = a;
        //cout << "arr[i] = " << arr[i] << " arr[min_index] = " << arr[min_index] << endl;


        //for(int i : arr ) {
        //    cout << i << " ";
        //}
        
        //cout << endl << endl;
    }

    for(int i : arr ) {

        cout << i << " ";
    }


輸出:5 17 33 41 55 61 80

一樣可以把註解打開，看看整個陣列是如何變化的

找最小值的動作會執行$\frac{n^2+n}{2}$次，而把最小值往前丟的動作會做n次，因此程式執行的次數為 $\frac{n²+3n}{2}$ 次 (n為陣列大小，也可以說是輸入的資料數)，時間複雜度為 O(n²)

例題:


範例輸出:


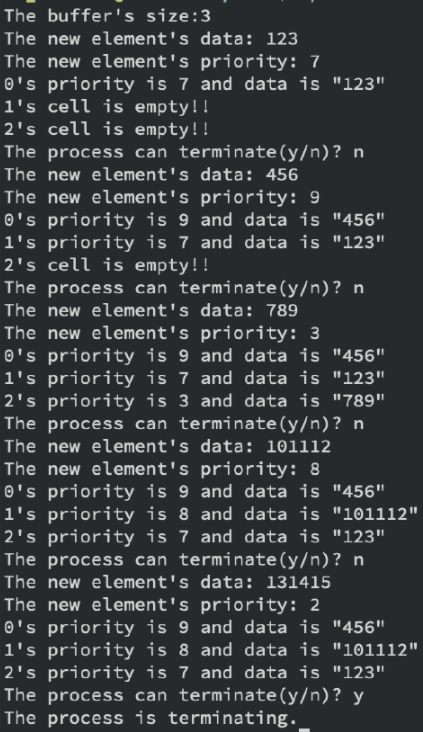
我的解答:

#include <iostream>
using namespace std;

void fSwap(int& p,int& q)
{
    int r = p;
        p = q;
        q = r;
}

int main()
{
    //建立初始陣列
    //ex:size=3
    //data=[-1 -1 -1 -1]  注意會有四格，最後一格拿來放輸入的值

    char yon;
    int size;
    cout << "The buffer's size:" ;
    cin >> size;

    int data[size+1];
    for(int i=0; i < size+1; i++) {

        data[i]= -1;
    }

    int pri[size+1];
    for(int i=0; i < size+1; i++) {

        pri[i]= -1;
    }

    int counter = 0;

    while(1) {

        cout << "The new element's data: ";
        cin >> data[sizeof(pri)/sizeof(*pri)-1];
        cout << "The new element's priority: ";
        cin >> pri[sizeof(pri)/sizeof(*pri)-1]; //輸入最後一格的值


        for(int k = 0; k < sizeof(pri)/sizeof(*pri) ; k++) {

            int max_index = k;
            for(int j = k+1; j < sizeof(pri)/sizeof(*pri) ; j++) {

                if(pri[j] > pri[max_index]) {
                    max_index = j;
                }
            }

            fSwap(pri[max_index], pri[k]);
            fSwap(data[max_index],data[k]);
        }

        for(int c=0; c < size; c++) {
                if(pri[c] != -1)
                    cout << c << "'s priority is " << pri[c] << " and data is \"" << data[c] << "\"" << endl;
                else
                    cout << c << "'s cell is empty!!\n";
            }

        cout << "The process can terminate(y/n)? ";
        cin >> yon;

        if(yon == 'y') {

            cout<<"The process is terminating.\n";
            break;
        }
    }

    return 0;
}

<br>

### 4-2. O(n²) —— 插入排序法

第二種方法是插入排序法，這個排序法也是只有兩個步驟，如下

1. 從「尚未排序的數字」中讀一個數
2. 把讀取的數往前插入一個位置

我們繼續使用 [41, 33, 17, 80, 61, 5, 55] 這個陣列，排序的情況見下圖

<a href="https://medium.com/appworks-school/%E5%88%9D%E5%AD%B8%E8%80%85%E5%AD%B8%E6%BC%94%E7%AE%97%E6%B3%95-%E6%8E%92%E5%BA%8F%E6%B3%95%E5%85%A5%E9%96%80-%E9%81%B8%E6%93%87%E6%8E%92%E5%BA%8F%E8%88%87%E6%8F%92%E5%85%A5%E6%8E%92%E5%BA%8F%E6%B3%95-23d4bc7085ff"><center><img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_40b71ff6ee843f25d01d29c6e8aea471.png"></center></a>

首先我們先宣告變數並建一個陣列，如下

    int i;
    int j;
    int a;
    int k;

    int arr[] = {41, 33, 17, 80, 61, 5, 55};

這樣我們就有一個未排序的陣列了，現在要開始用插入排序法來排序，如下

    for(i=1; i < sizeof(arr)/sizeof(*arr); i++) {

        //cout << " i= " << i << endl;
        k = i;
        
        while( k > 0 && arr[k] < arr[k-1]) {

            //cout << " k= " << k << " 符合條件 "<< endl;
            a = arr[k];
            arr[k] = arr[k-1];
            arr[k-1] = a;
            //cout << "a = " << a << " arr[k] = " << arr[k] << " arr[k-1] = " << arr[k-1] << endl;
            k--;

            //for(auto j:arr) {
            //    cout << j << " ";
            //}
            //cout << endl << endl;
        }

    }

    for(auto j:arr) {
        cout << j << " ";
    }

    cout << endl << endl;


    return 0;


輸出:5 17 33 41 55 61 80

一樣可以把註解打開，看看整個陣列是如何變化的
「插入合適位置」需要 1+2+3+…+n 個步驟，而「讀一個數字」需要 n 個步驟，因此程式執行的次數為 $\frac{n²+3n}{2}$ 次 (n為陣列大小，也可以說是輸入的資料數)，時間複雜度為 O(n²)

<br>

### 5-1. O(n logn) —— 快速排序法(Quick Sort)

第三種方法是快速排序法，這是一個很常使用的排序法，他是一種「把大問題分成小問題處理」的Divide and Conquer方法，

Quick Sort的步驟主要有兩步
+ 在數列中任意挑選一個數，稱為pivot，然後調整數列，使得「所有在pivot左邊的數，都比pivot還小」，而「在pivot右邊的數都比pivot大」。

+ 接著，將所有在pivot左邊的數視為「新的數列」，所有在pivot右邊的數視為「另一個新的數列」，「分別」重複上述步驟(選pivot、調整數列)，直到分不出「新的數列」為止。

<center><br>
<img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_02897ab90d8ce2c5dec817bd1180b08f.png">
</center>
<br>

以上圖為例，考慮數列{9、4、1、6、7、3、8、2、5}，先任意選定5為pivot，接著調整數列，使得pivot左邊的數{4、1、3、2}皆小於5，而pivot右邊的數{9、8、6、7}皆大於5。

那我們該如何做到這件事?這時候就要介紹「調整數列」的方法了，俗稱Partition。

Partition的思路就是把數列「區分」成「小於pivot」與「大於pivot」兩半。

詳細步驟如下:

定義變數(variable)

<center><br>
<img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_6bf64dceec5987470d8c6893fdaf12ed.png">
</center><br>

+ int pivot = array[end]，以數列最後一個數做為pivot，pivot的「數值」可以是任意的，挑選矩陣的最後一個位置是為了方便index(j)的移動，也可以挑選任意位置。

+ int front為數列的「最前端」index。
+ int end為數列的「最尾端」index。
+ int j是讓pivot與其餘數值逐一比較的index，從front檢查到end-1(因為end是pivot自己)。
+ int i是一個旗子(檢查點)，一開始設為-1，當發現了比pivot小的數值(arr[j])時，便將旗子往後插一格(i++)，然後把arr[i]與arr[j]互換，當演算法要結束時，將arr[i]與pviot的互換，因此當演算法結束時，所有在index(i)左邊的數，都比pivot小，所有在index(i)右邊的數，都比pivot大。

可以參考下面的圖<br>

<center>
<img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_985cd27cb0f88ef92951a3f3f8851b5c.png
">
</center><br>

最後，將pivot與arr[i]互換就完成了調整<br>

<center>
<img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_9c361540f2c6fb08a779ea210f5fc300.png
">
</center><br>

接下來只要對「左數列」與「右數列」重複執行這些動作，就能完成整個數列的調整啦！

<center>
<img src="https://codimd.mcl.math.ncu.edu.tw/uploads/upload_72aa03d7b0ef5e0e6a253f81ac85021d.png
">
</center><br>

範例程式碼於下，我把i的初始值設為0了

#include <bits/stdc++.h>
using namespace std;

void Quicksort(int arr[], int front, int end);
int Partition(int arr[], int front, int end);
void swap(int *a, int *b);

int main() {

    int arr[10] = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};
    int front = 0;
    int end = sizeof(arr) / sizeof(*arr)-1;

    Quicksort(arr, front, end);
    
    //印出被改變後的陣列
    for(auto n : arr)
        cout << n << " ";
        
    system("pause");
    return 0;
}

void Quicksort(int arr[], int front, int end) {

    if (front < end){
        int pivot = Partition(arr, front, end);
        //排列每個左邊的陣列
        Quicksort(arr, front, pivot-1);
        //排列每個右邊的陣列
        Quicksort(arr, pivot + 1, end);
    }
}

int Partition(int arr[], int front, int end) {
    
    //把pivot設在最後一個數
    int pivot = arr[end];
    //先把旗子插在第一格
    int checkpoint = front;
    
    //掃描
    for (int i = front; i < end; i++) {
        //如果找到了比pivot小的數就交換數值並插旗
        if(arr[i] < pivot) {
            swap(&arr[checkpoint], &arr[i]);
            checkpoint++;
        }
    }
    //最後要交換pivot和旗子位置的值
    swap(&arr[checkpoint], &arr[end]);

    return checkpoint; //回傳最後pivot的位置
}

void swap(int *a, int*b) {
    int temp = *a;
    *a = *b;
    *b = temp;
}

<br>

### 5-2. O(n logn) —— 合併排序法(Merge Sort)

<br>

### 6. O(2$^n$) —— 費氏數列遞迴

<style>

.green {
color:#29E5A9;
}

.brown {
color:#990000;
}

.pink {
color:#DD9FBD;
}

.red {
color:#E71B18 ;
}

.blue {
color:#0b5394;
}

.purple {
color:#AC9FDD;
}

@-webkit-keyframes A
{
0% { color:#C10066;}
10% { color: #CC0000;}
20% { color: #E63F00; }
30% { color:#EE7700; }
40% { color: #DDAA00; }
50% { color:#EEEE00;}
60% { color: #99DD00;}
70% { color:#66DD00;}
80% { color: #00DDDD;}
90% { color: #0044BB;}
100% { color: #A500CC;}
}

#animation_title{
animation: A 3s ease 0s infinite alternate;
-webkit-animation: A 3s ease 0s infinite alternate;
}

</style>

<style>

a.redlink {
color:#DB1859;
}

a.redlink:link {
color:#DB1859;
text-decoration:none;
}

a.redlink:visiteid {
color:#DB1859;
text-decoration:none;
}

a.redlink:hover {
color:#19CABC;
text-decoration:none;
}

a.redlink:active {
color:#000000;
text-decoration:underline;
background:#FFFFFF;
}

</style>

<style type="text/css">

h1 {
font-size:;
color:#0b5394;
}

h2 {
font-size:;
color:#0b5394;
}

p {
font-size:;
color:;
}

h3 {
font-size: ;
color:#990000;
}

h4 {
font-size:;
color:#990000;
}

</style>