---
tags: vaje, rg, delaunay
hackmd: https://hackmd.io/MDZkJm80SwSw60kZXUmCCQ
plugins: mathjax
---
# Computational geometry - Tutorial 19.5.2021

---

## Delaunay triangulation

* vertices: sites of the Voronoi diagram
* we have an edge whenver the two corresponding cells of the Voronoi diagram have a common boundary

---

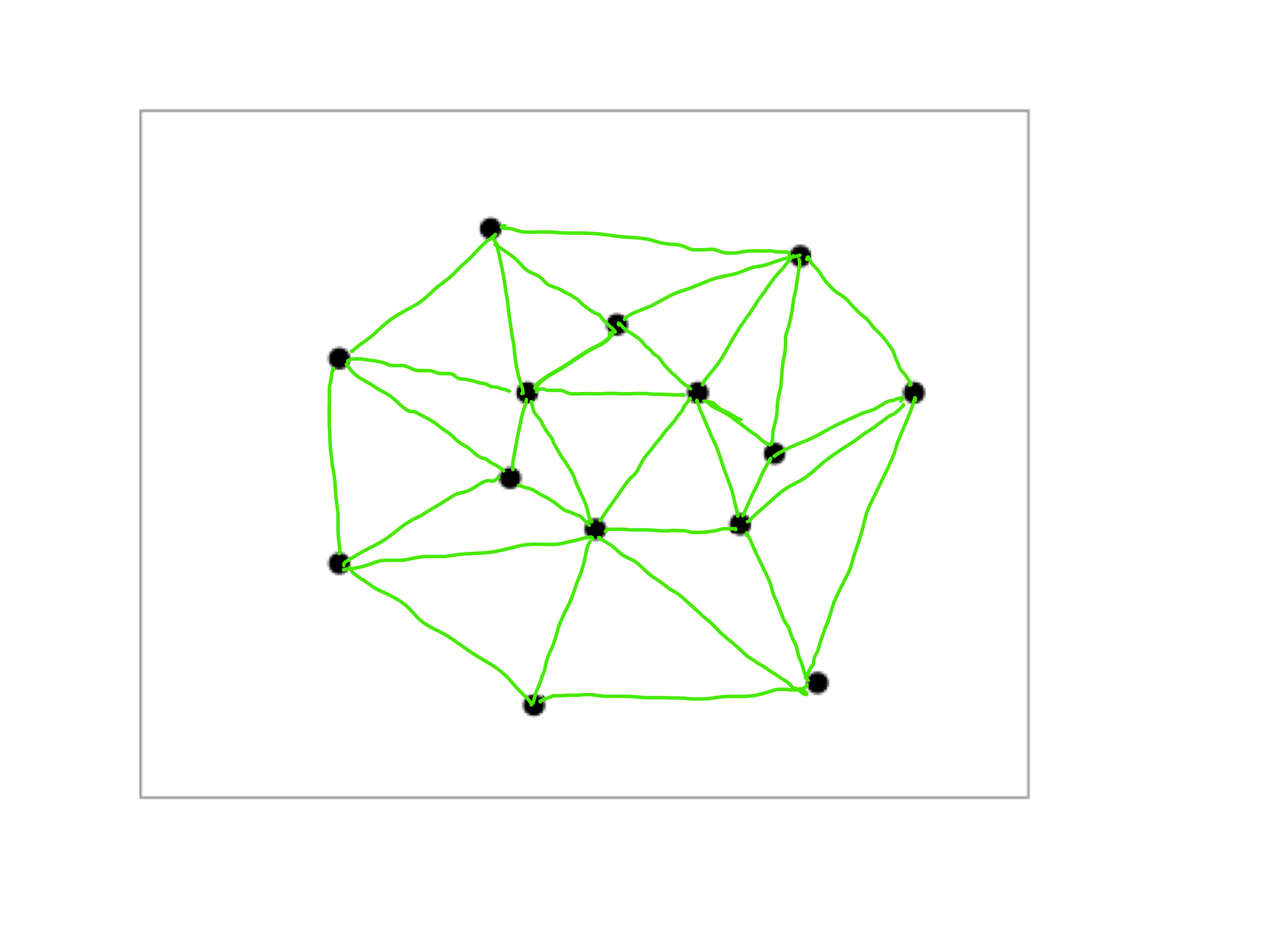
### Exercise 1

Draw the Delaunay triangulation of the point set from the drawing below.


----


---

### Exercise 2

For $i=1, \dots, 100$, choose the coordinates of the points ${p_i} \in \mathbb{R}^2$ in such a way that the Delaunay triangulation of the set $\lbrace {p_1}, {p_2}, \dots, {p_{100}} \rbrace$ contains at least two points of degree $99$. The points should be in general position: no three points are collinear and no four points are concyclic. Carefully argue that your choice of points has the desired properties.

----


---

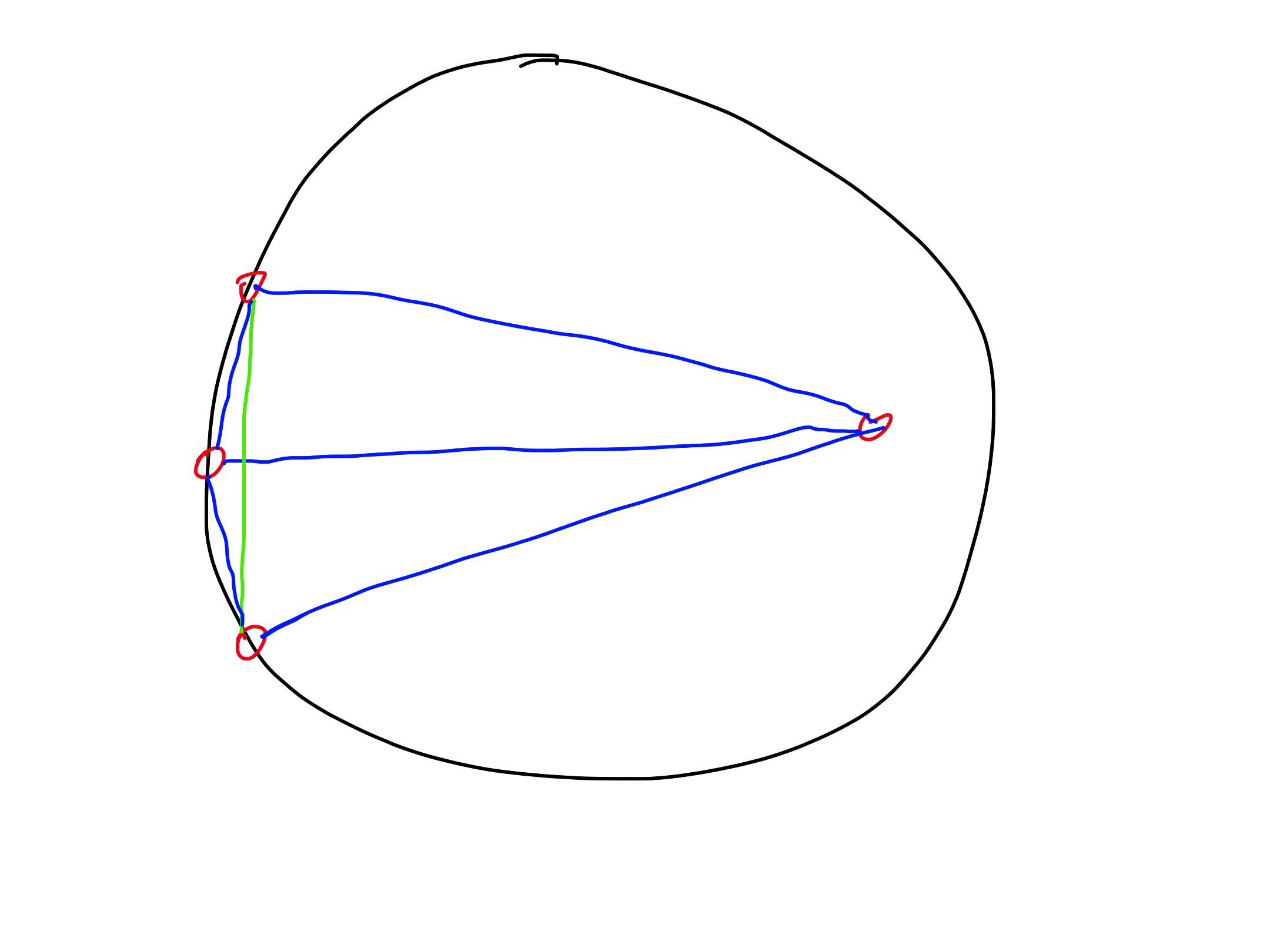
### Exercise 3

Let $P$ be a set of points in a plane. Its _shortest_ triangulation is such a triangulation that minimizes the sum of edge lengths. Prove that the shortest triangulation is not necessarily a Delaunay triangulation.

----


---

### Exercise 4

Let $P = \lbrace {p_1}, {p_2}, \dots {p_n} \rbrace$ be a set of $n$ points in a plane. Assume the following general position: if $\lbrace {p_i}, {p_j} \rbrace \ne \lbrace {p_{i'}}, {p_{j'}} \rbrace$, ${p_i} \ne {p_j}$, ${p_{i'}} \ne {p_{j'}}$, then $d({p_i}, {p_j}) \ne d({p_{i'}}, {p_{j'}})$, where $d(\cdot,\cdot)$ is the Euclidean distance. The minimum distance ${d_{\min}}$ in $P$ is

$$
d_{\min} = \min\{d(p_i, p_j) \mid p_i \ne p_j\}.
$$

We define the second smallest distance ${d_{2.\!\min}}$ in $P$ as

$$
d_{2.\!\min} = \min\left(\{d(p_i, p_j) \mid p_i \ne p_j \} \setminus \{d_{\min} \}\right).
$$

Describe an algorithm which computes the second smallest distance ${d_{2.\!\min}}$ in $O(n \log n)$ time.

----

* Compute the Delaunay triangulation of $P$ ($O(n \log n)$)
* Find the edge ${p_i} {p_j}$ of minimal length ${d_{\min}}$ ($O(n)$)
* Compute the Delaunay triangulations of $P \setminus \lbrace {p_i} \rbrace$ and $P \setminus \lbrace {p_j} \rbrace$ ($O(n \log n)$)
* Find the shortest edge in these two triangulations, its length gives ${d_{2.\!\min}}$ ($O(n)$)


---

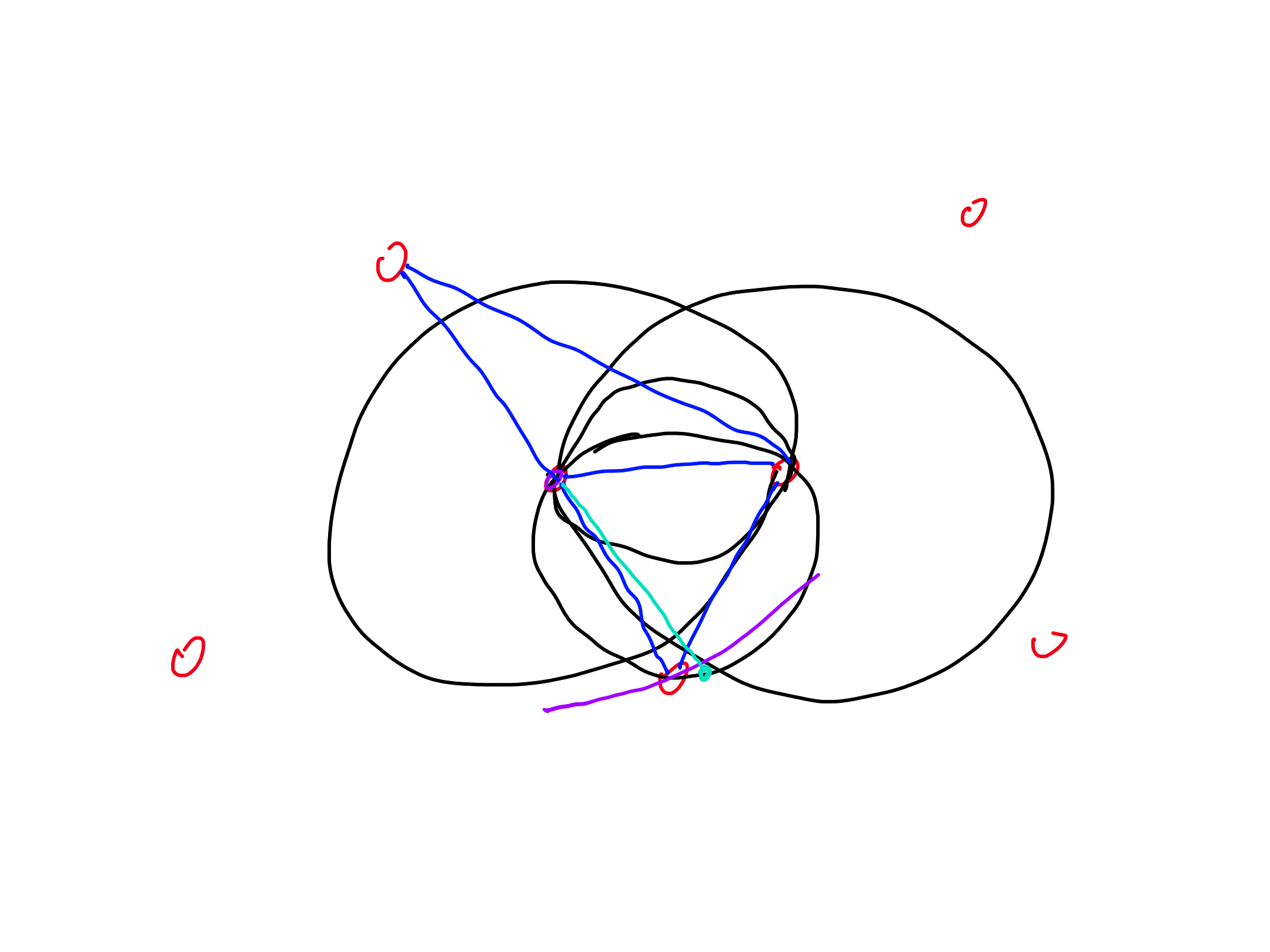
### Exercise 5

Let $P$ be a set of $n$ points in a plane. The _Gabriel graph_ $G(P)$ for $P$ has vertex set $P$ and an edge between $p$ and $q$ if and only if the disk with diameter $pq$ does not contain any point of $P \setminus \lbrace p, q \rbrace$.

1. Show that $G(P)$ is a subgraph of the Delaunay triangulation of $P$.
2. Show that $pq$ is an edge of $G(P)$ if and only if the Voronoi faces of $p$ and $q$ have a common edge $e$ and the segment $\overline{pq}$ intersects $e$.
3. Describe an algorithm which returns $G(P)$ in $O(n \log n)$ time.
4. Show that at least $\Omega(n \log n)$ time is required to compute the Gabriel graph.

----


1. If the disk with diameter $pq$ contains not point from $P \setminus \lbrace p, q \rbrace$, then we can enlarge it, keeping $p, q$ on the boundary, until it meets another point giving a Delaunay triangle, implying that $pq$ is a Delaunay edge.
2. $\overline{pq}$ intersects $e$ if and only if the intersection (the midpont of $\overline{pq}$) is nearest to $p$ and $q$.

---

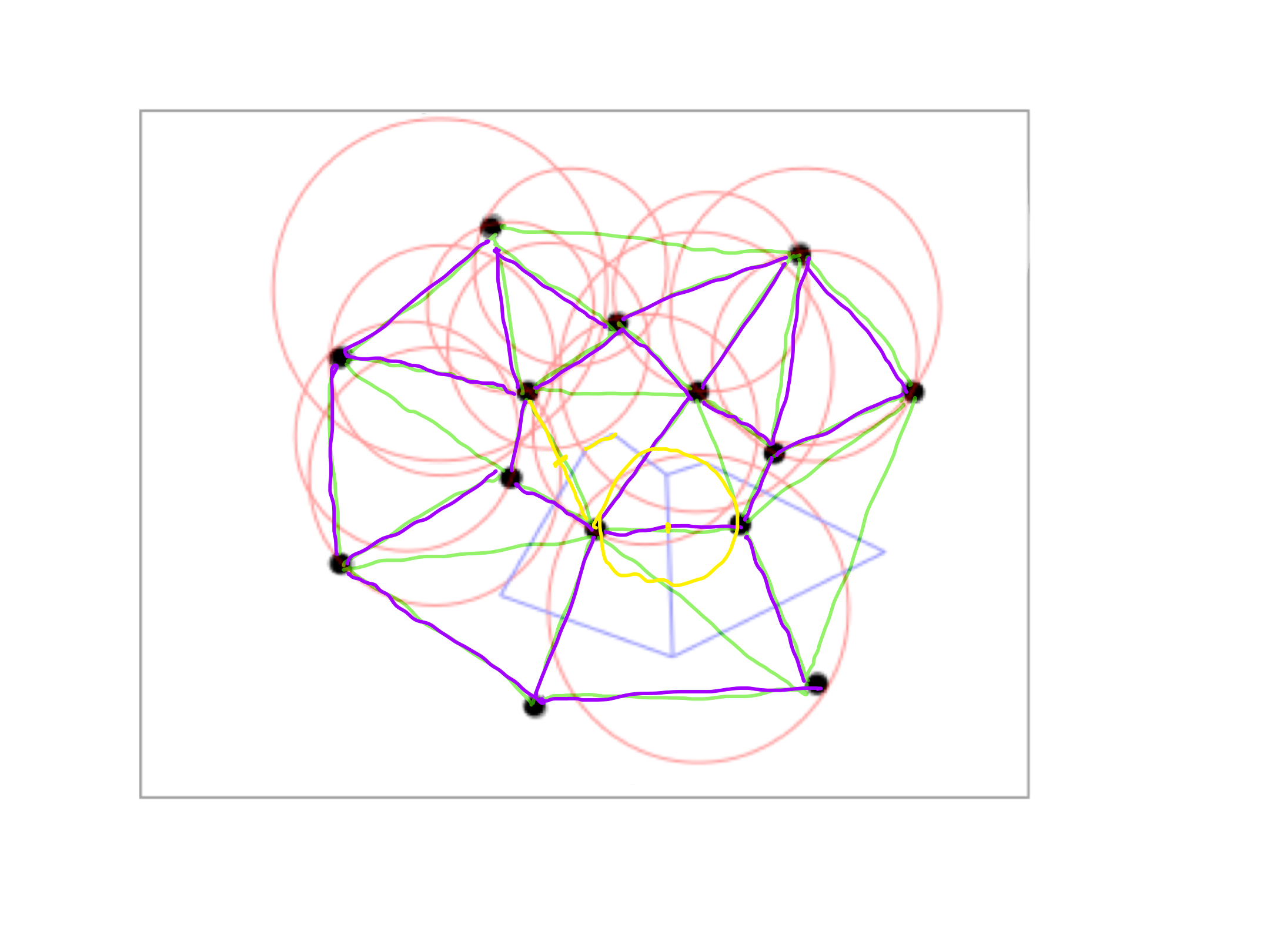
### Exercise 6

Let $P$ be a set of $n$ points in a plane. Describe an algorithm for finding the smallest disk $D$ containing at least four points of $P$,
with at least three of these points lying on the boundary of $D$. Your algorithm should run in $O(n \log n)$ time.

**Hint:** which Delaunay triangulations will be useful?