owned this note
owned this note
Published
Linked with GitHub
# ZK Fixed Point Arithmetic with its Application in Machine Learning
## 0x0 Introduction
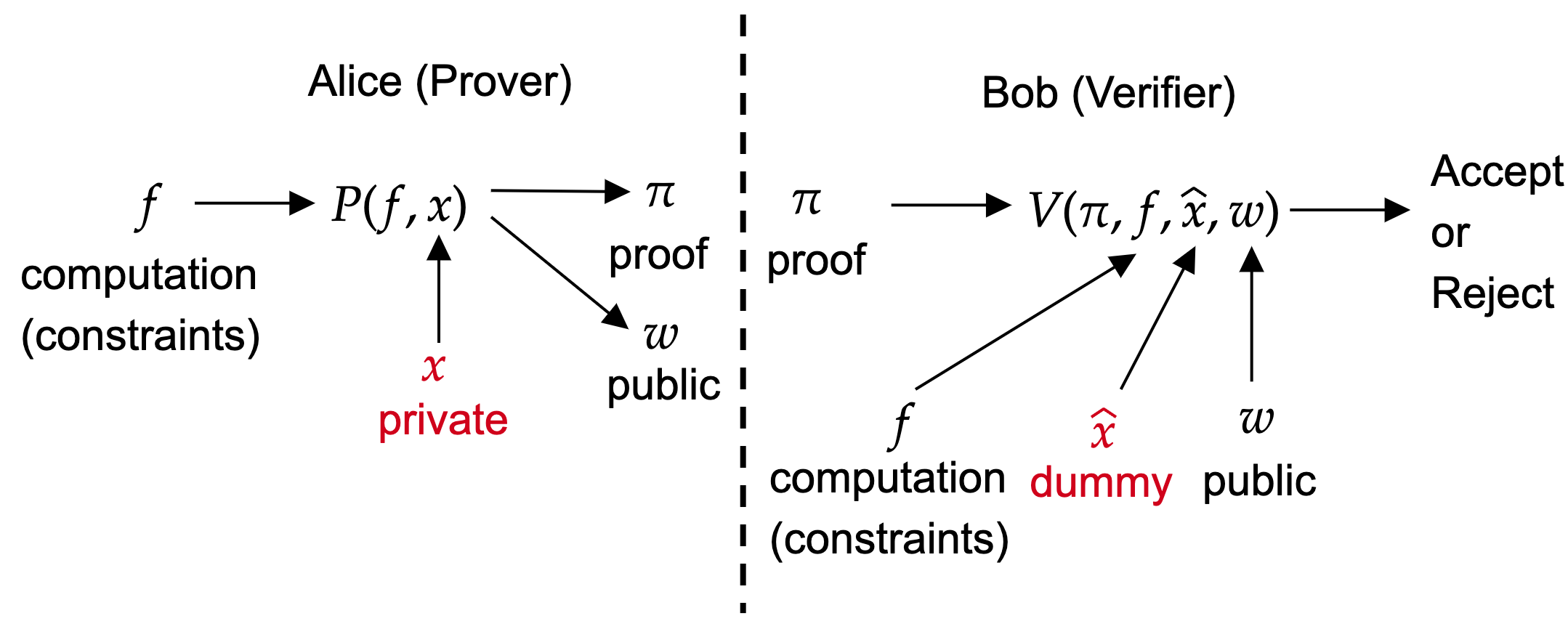
Alice wants to prove that she knows some private information and public information which passes given computations or constraints. And Bob can verify the proof provided by Alice without revealing any private information. So in such scenario, we need **zero knowledge proof (ZKP)**. The key properties of ZKP are two things.One is the computation could be hard or expensive, and the verification is very cheap. We call it **succinctness**. For blockchain, it’s really useful for verifying an expensive computation in smart contract. This is what zkEVM does in Layer-2 blockchain as we can run a program in off-chain zkEVM and also generate the proof off-chain. And then we only need a cheap gas fee for verifying it on-chain. Another property of ZKP is the **zero knowledge**. Because the verifier does not need to know the private. It’s useful in user-privacy preserving scenario. Take ZK version of Kaggle as an example, a user can use ZKP to prove that he has a machine learning model which gets 99% accuracy on an image classification task but he does not want to public his valuable model to the verifier. It’s also note that the public includes input, output, and any intermediate variable in computation. So it’s useful for public some important results along with the proof.
With the rapid development of various AI technologies and their amazing capabilities, how to combine them with cutting-edge cryptography and blockchain technologies to improve their security and transparency is a much-needed and promising direction. Leveraging zero knowledge to proetct private information while keeping it's verifiability for machine learning algorithms is what **ZKML** does. Daniel Kang's blog [9] privdes us a good example to verify the algorithmic integrity of Twitter’s recommendation results with zkml. Although Twitter open-sourced their algorithm, if Twitter generates "For You" timeline with other models instead of the public version they guaranteed, they are able to manipulate bias and content censorship. We were able to ensure via ZKP that Twitter was not secretly using a malicious alternative recommendation model.
All operations in machine learning models are related to float numbers. But all the operations in [Halo2](https://github.com/privacy-scaling-explorations/halo2.git)'s ZK circuit are natively in BN254 field which is a finite unsigned integer type. Implementing fixed/float point arithmetic is an important basic for any type of ML or numerical algorithm. Because the ZK proof system only accept ZK circuit which consists of many constraints that only support `+`, `-`, `*`, and `=` operations over BN254. So if we want to use ZK proof system to proof our computation, we must find a way (arithmetization) to transform the computation to ZK circuit with ZK language. The transformation is what this project does.
This project provides an easy-to-use fixed point arithmetic chip based on Halo2. Fixed point numbers will be automatically represented with BN254 numbers. It provides basic operations (multiplication, addition, subtraction, division) and also implements a large number of commonly used nonlinear functions (e.g., `log`, `sin`) using the ZK primitive. To show the power of the implemented fixed point arithmetic, this project leverages it to implement the most representative machine learning algorithms, including linear regression, logistic regression, and decision tree. In addition to the inference of these algorithms, this project also implements the more challenging and ambitious training process.
As an overview, this project provides four useful chips (aka., ZK circuits):
* FixedPointChip: Fixed point arithmetic and math library
* Support different kinds of precisions (from `32.32` to `63.63`) with automatically generated polynomial using [Remez algorithm](https://en.wikipedia.org/wiki/Remez_algorithm)
* Support negative number arithmetics with quantization
* Support functions: `add`, `sub`, `mul`, `div`, `mod`, `sign`, `clip`, `polynomial`, `bit_xor`, `sum`, `neg`, `exp`, `log`, `pow`, `sqrt`, `max`, `sin`, `cos`, `tan`, `sinh`, `cosh`, etc.
* ZK-LR: LinearRegressionChip/LogisticRegressionChip
* Support inference with vector multiplication and `sigmoid` (based on `exp`) using FixedPointChip
* Support training with gradient descent algorithm
* ZK-DT: DecisionTreeChip
* Support inference with tree traversal over the decision tree
* Support training by building the decision tree recursively with the calculated Gini Impurity in each node
There are two demonstrations presenting the training process of ZK linear regression and ZK decision tree. To run the demo and develop your own ZK circuit based on this project, please check out [ZKFixedPointChip](https://github.com/DCMMC/ZKFixedPointChip).
### Demo of ZK linear regression training
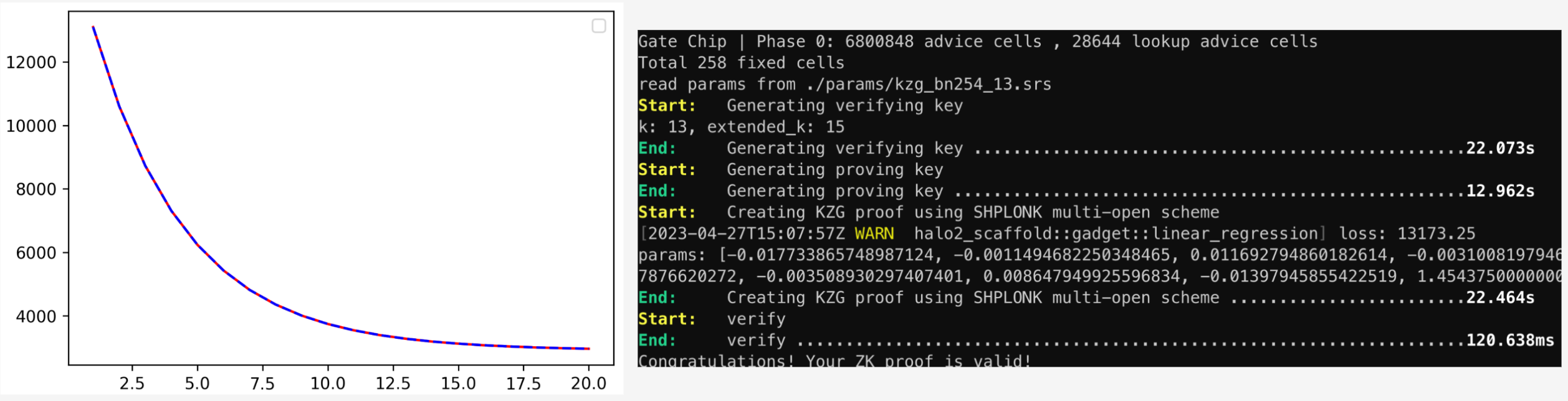
The training of linear regression has a closed form solution, but the solution involves matrix inverse operation which has the ill-conditioned problem leading to numerical unstable. This project implements linear regression training with SGD (Minibatch Stochastic Gradient Descent). If we generate the whole training process (e.g., 50 epochs and 32 batchs per epoch need 1600 training steps) with just one proof, the computation complexity of proving is too high. So I split the whole training process into multiple step proofs. One step proof stands for one batch or multiple batchs. With the help of [AggregationChip](https://github.com/scroll-tech/halo2-snark-aggregator), the whole training process can be represented with one proof aggregating all the step proofs. The above figure shows the loss curve when training linear regression model. To perform sanity checks of my implementation, I also implement a non ZK version and compare the loss values of both implementation in each training step. In the figure, the blue dashed line is ZK version of linear regression and the red solid line is the non-ZK version. We can see the error is negligible and it shows the correctness of my ZK implementation.
### Demo of ZK decision tree training
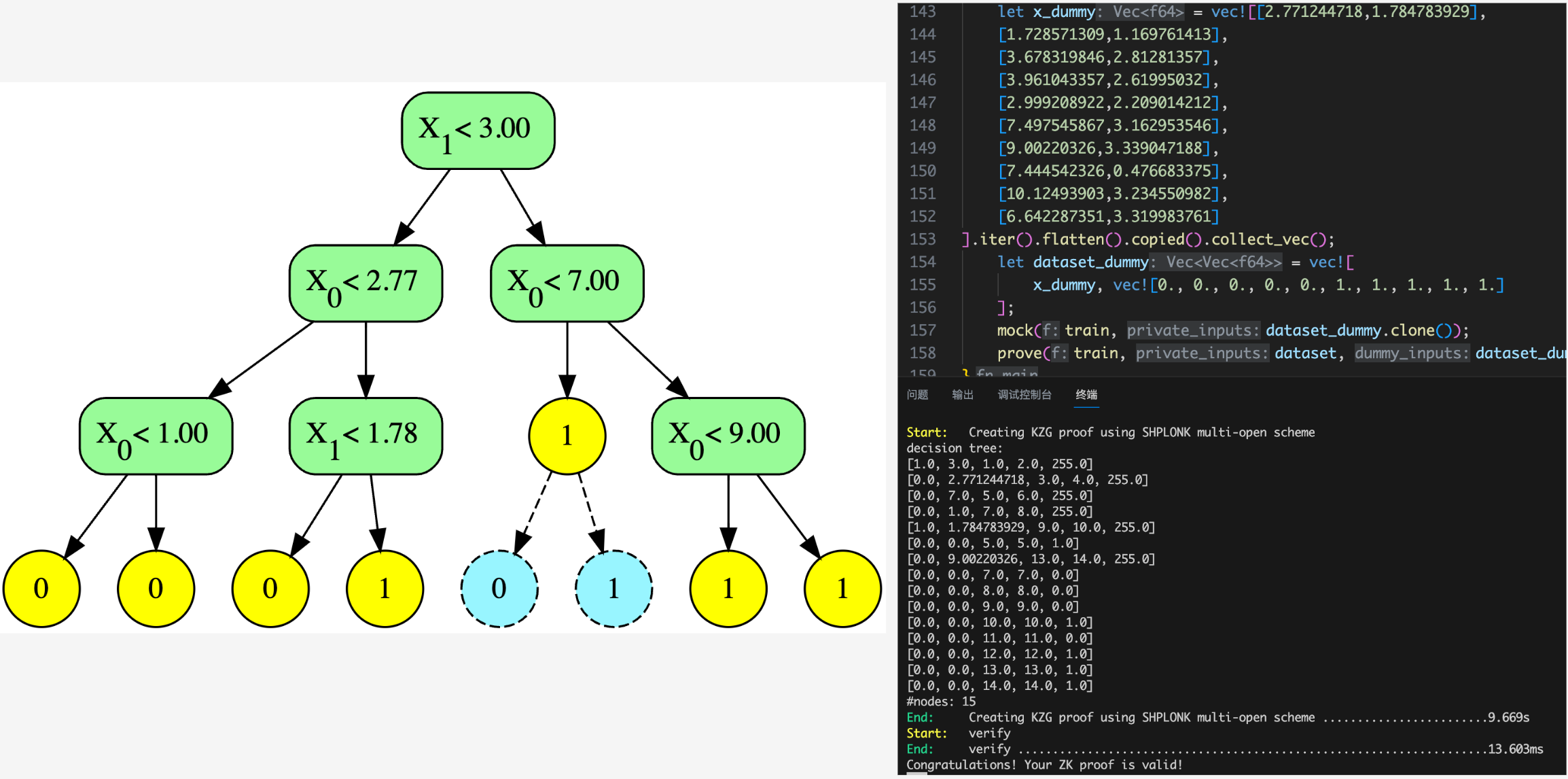
Training of decision tree is quite different with linear/logistic regression. Decision tree is a binary tree (or multiway tree but is ignored in this project). This project exposes easy-to-use interfaces for inferencing and training decision tree with a given dataset and hyper-parameters (e.g., max depth). There are different kinds of decision tress and its training algorithms. For simplicity, this project chooses to implement CART training algorithm [8]. It also references the Python implementation provided by Jason Brownlee[2]. To visualize the generated decision tree and compare it with the one generated by Python version, the decision tree will be automatically exported with `dot` language and `graphviz` is used to convert it to `svg` figure. The node with yellow circle is leaf node, the green node is splitting node, and the blue one is fake node. For more details, please refer to the implementation section.
### Benchmark
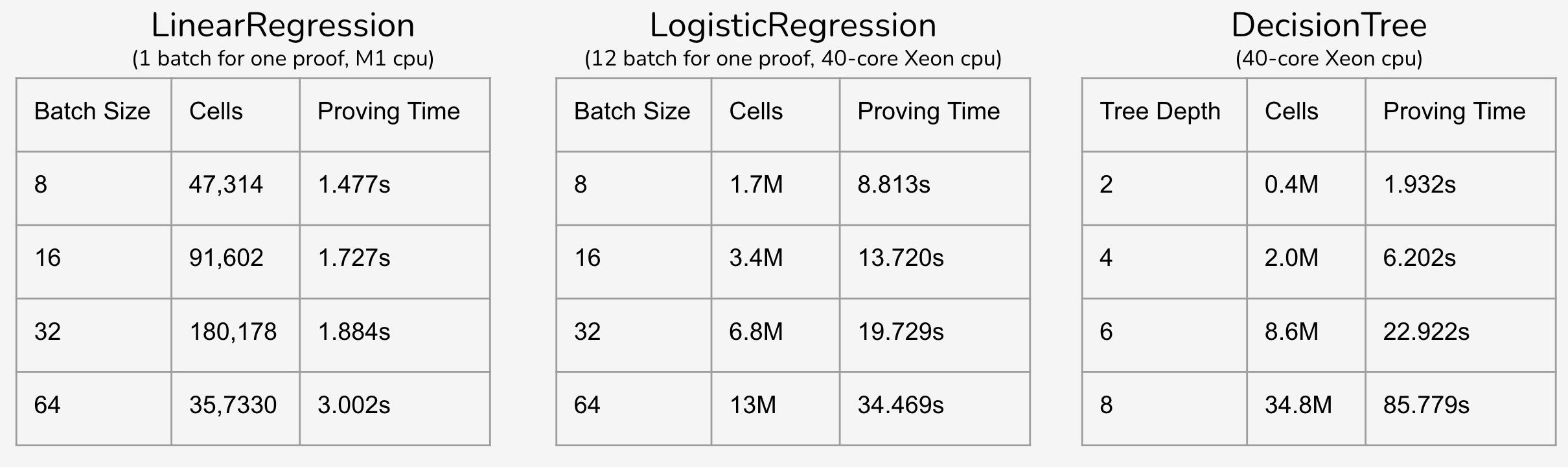
To explore the computation complexity and performance of this project, I conduct the benchmark for the training of linear regression, logistic regression, and decision tree. From the results, increasing batch size will save some proving time for the whole training process.
## 0x1 Motivation & Challenge
### Motivation
* support for fixed point arithmetic is important for any type of ML or numerical algorithm
* most existed ZKML projects focus on deep learning
ZK circuit in `halo2` only supports `+`, `-`, and `*` operations over BN254. That means, development of ZKP lacks support for float/fixed point operations. Compared with fixed point operations, floating-point operations introduce a lot of unnecessary computation overhead. For simplicity, I select to implement ZK fixed-point arithmetics using `halo2`. This project provides not only basic fixed-point arithmetics (`add`, `sub`, `div`, `mod`, `mul`), but only complex operations (e.g., `sin`, `exp`, `log`). Fixed point arithmetic is an important basic for any type of ML or numerical algorithm.
On the other hand, most existed ZKML projects focus on deep learning instead of traditional machine learning algorithms. Transforming original float-point deep learning models into integer-only models is a widely researched and applied technology. This is called **quantization**. There are many existed tools such as Tensorflow and PyTorch provide model quantization. For most existed ZKML projects, they only support deep learning models and the models must be quantized first. And for non-linear functions, directly quantizing them is basically impossible. There are some projects or researches [5] propose to implement them with polynomial approximation. Many of the existed ZKML projects instead use `lookup` tables to implement them. In addition, for many traditional ML algorithms such as decision tree, it's hard to quantize the whole model. With `FixedPointChip` in this project, ZK developers can easily develop ZK versions of ML algorithms without caring about quantization and the implementations of most commonly used non-linear functions. For ZKML developers, this project also implements some examples showing how to use `FixedPointChip` to develop ZKML algorithms (see implementations in `LinearRegressionChip`, `LogisticRegressionChip`, and `DecisionTreeChip`). For ZKML users or other ZK developers who want to use out-of-the-box ZKML algorithms directly in downstream applications or ZK circuits, they can directly pick this project.
### Challenge
* quantization is not easy for non-linear functions
* transform all quantization operations into BN254 operations in ZK circuit ways
* decision tree relies on variable length of traversal path and recursion to build the tree
* carefully debug and sanity checks
The challenges of this project are in several folds. As shown in the motivation, quantization is not easy for non-linear functions. A mainstream solution is using high-degree polynomial to approximate the non-linear function in a given input range. For a input number, it should be first tranformed to this given input range and then calculate the output of the polynomial. Second, ZK circuit only supports BN254 opeartions.I need to transform all quantization operations into BN254 opeartions in ZK circuit ways. I need to not only just finish this transformation correctly, but also find a ZK-friendly way. Becuase most fast operations in normal programs are slow and hard to implement in ZK circuit, like logic `and` and `xor`.
Third, variable length operations and recursion are ZK-unfriendly. They can not directly be supported. Decision tree relies on them to train and build the whole tree. When inferencing, it also requires traversal on paths with different lengths. To solve this challenge, this project proposes path padding and fake nodes. Path padding is used for making every traversal paths having the same legnths. And fake nodes are added to the original decision tree to make the tree be a complete binary tree. Finally, developing ZK circuit using `halo2` needs carefully debug and sanity checks. `Halo2` is still a very new project, so it's hard to debug when facing errors. It requires us to carefully write codes and debug. For example, if we make the generate circuits different between proving and verifying, it will complaint `ConstraintFailure` error without telling us which line in the source code leads to this error. To verifying the correctness of the implementation, it's necessary to write sanity checks comparing the ZK version and non-ZK version.
## 0x2 Implementation
### FixedPointChip
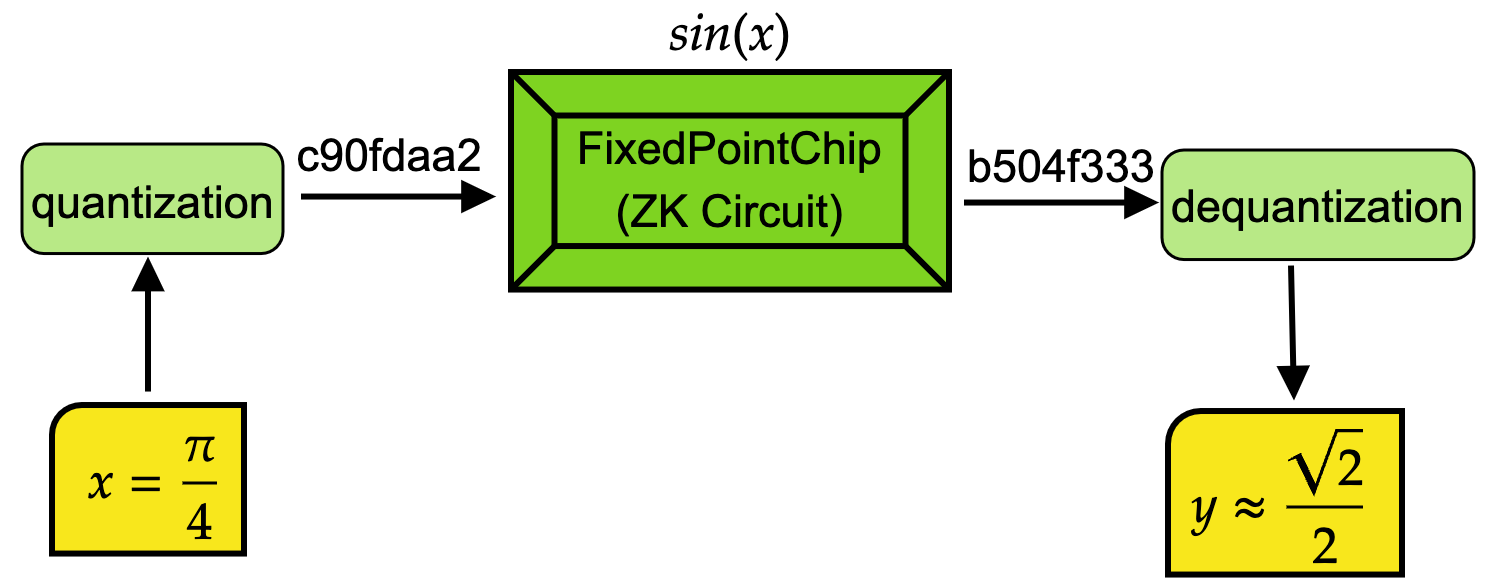
* Symmetric quantization
* Representation of negative numbers
* Basic operation, Basic function, Derived function
* Polynomial approximation & argument reduction for non-linear functions
The overview workflow of operations in `FixedPointChip` is shown in the above figure. If we want to calculate $\sin(x)$ using `FixedPointChip`, we first quantize the input decimal number and then feed to `FixedPointChip` to get the output. The output is also quantized number stored in a BN254 integer. With the help of `dequantization`, we will get the final output in the format of decimal number. It's note that all the operations in green color are automatically done by this project. The user only need to input the original decimal number and the get decimal output.
To implement `FixedPointChip`, first thing is how to represent decimal numbers with BN254 integer numbers. The transformation from decimal numbers to BN254 numbers is called `quantization`. And `dequantization` is the inverse operation. The formula of `quantization` and `dequantization` is presented in the following figure:
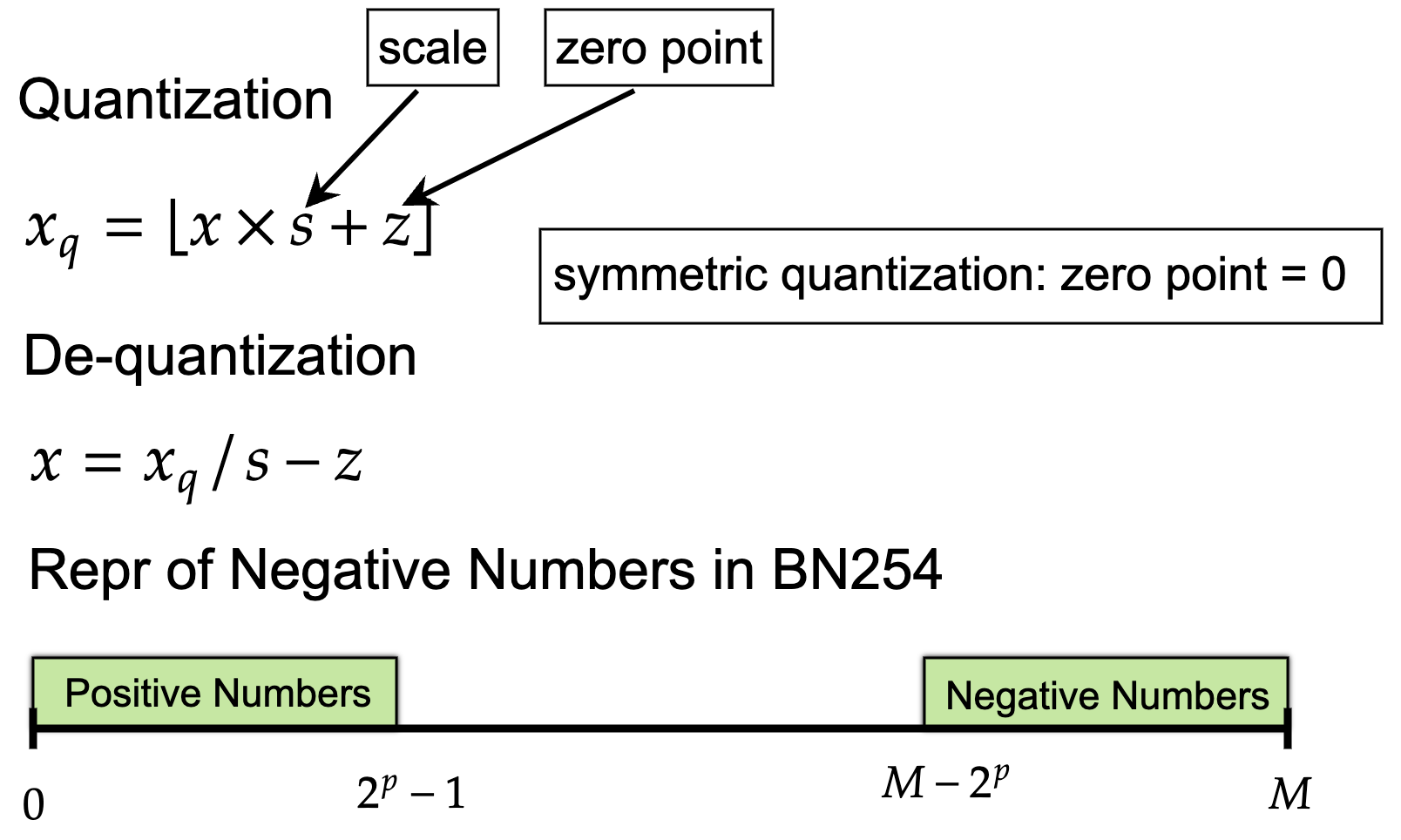
The decimal number is $x$ and the quantized BN254 number is $x_q$. We call $s$ scale and $z$ zero point. If $z=0$, we call it symmetric quantization, otherwise it's asymmetric quantization. If we have a computation (e.g., $\sin(x)$) which is originally designed for decimal numbers, but how can we transform it to let the computation only contains BN254 operations? This is called the quantization of this computation. Take mulitiplication as an example. Here is the quantizations of `mul` in symmetric quantization and asymmetric quantization:

Because the tranformed computation should only contains the quantized numbers and the output should be the quantization of the decimal output of the original computation. The disadvantage of symmetric quantization is the range of the quantization results include negative fields because the range of input decimals include negatives. So in design, we need to deal with negative numbers in BN254. Because BN254 is a finite cyclic group whose range is $[0,M]$ where $M \approx 2^{254}$, it does not support negative numbers natively. Thanks to BN254 supports modulo, negative numbers can be transformed to the valid range by modulo (i.e., $M-x$). But in implmentation, we need to keep the negative fields in our mind and carefully process them which will bring more computation overheads. Symmetric quantization has the advantage that the computation is simpler as you can see the computation for asymmetric quantization takes more computation terms. Compared with symmetric version, asymmetric quantization has the ability to transform the input into a positive range so we do not need to worry about how to deal with negative numbers. It's a trade-off betwen both versions. This project selects symmetric quantization.
To ensure that the ranges of positive numbers and negative numbers do not overlap, this project supports a maximum precision of $63$. To ensure the error in a small range, the minimum precision is $32$. $p$ in the figure denotes the precision.
All the operations in `FixedPointChip` can be splitted into three categories: basic operations, basic functions, and derived functions. Basic operations include four basic arithmetics: `mul`, `div`, `mod`, `add`, and `sub`. For the detail implementation of `mul`, the quantization formula is: $c_q = \frac{a_q \times b_q}{s}$. To support negatives, we know modular multiplication property: $(a*b)\,mod\,n=(a\,mod\,n)*(b\,mod\,n)$. But the division does not has this nice property, we must implement it with ZK circuit manually. I call this signed division $c = \frac{a}{b}$ where $a$ might be negative number and $b$ is postive number. Like `div_mod` in Axiom's `halo2-base`, I first decompose $a$ to $a = b \times q + r$ where $r > 0$ and $q$ could be negative number. If $a$ is negative number, thanks to modular multiplication property, then $a\,mod\,M = b \times (q\,mod\,M) + q$. With this decomposition as ZK constraint, we can safely support signed division and the $q\,mod\,M$ is the output.
With basic operations, the next step is implementing basic functions:
* `sin`
* `exp2`
* `log2`
To implement these basic functions, as they are non-linear functions, we cannot directly make quantizations for them. Like the implementation in I-BERT [5], `FixedPointChip` first uses [Remez algorithm](https://en.wikipedia.org/wiki/Remez_algorithm) to find the optimal polynomial approximation for the basic function. Polynomial only contains quantization `+` and `*` so we can just use basic operations in `FixedPointChip` to implement it. The coefficients in the optimal polynomial is pre-computed and fixed in the `FixedPointChip` because the coefficients of the polynomial do not need to be changed for different precisions and inputs. Meanwhile, the Remez algorithm can only find the optimal approximation in a given input range (e.g., $[2,4]$) which is smaller than the domain (e.g., $\mathbb{R}$) of the function. To make the approximation support for the domain of the function, it also needs some transformation for the input. Take `log2` as an example. the workflow of its implementation is as follows:
* Use Remez algorithm to find the optimal polynomial approximation $\text{ploy_log2}$ for `log2` over the range of $[2, 4]$
* Argument reduction: for the input x, we need to find a bound $2^n \le x < 2^{n+1}$ and then decompose $x$ into $x=k \times 2^m, m \in \mathbb{Z}, 2 \le k < 4$
* The final computation is $\text{log2}(x) = \text{ploy_log2}(k)+m$
Once we have basic operations and basic functions, we can easily use them to implement many kinds of derived function. A list of the derived functions in `FixedPointChip` is shown in below:
* $cos( x) =sin\left( x+\frac{\pi }{2}\right)$
* $tan( x) =\frac{sin( x)}{cos( x)}$
* $exp( x) =exp2\left(\frac{x}{ln2}\right)$
* $log( x) =\frac{log2( x)}{log2( e)}$
* $pow( x,\ a) =exp( a\times log( x))$
* $sqrt( x) =pow( x,\ 0.5)$
* $sinh( x) =\frac{exp( x) -exp( -x)}{2}$
* $\cdots$
* $cosh( x)$
* $tanh( x)$
### ZK-LR: LinearRegressionChip, LogisticRegressionChip
* Inference
* Based on inner_product, qexp, qsum, qmul, qadd, qdiv in FixedPointChip
* Training
* Based on mini-batch gradient descent. Generate one proof for multi batches, and use AggregateCircuit to generate the final proof for the whole training
The formulas of linear regression and logistic regression are:
* Linear regression: $w^\top x + b$
* Logistic regression: $\sigma(x^\top x + b, \sigma(x) = \frac{1}{1+\exp(-x)})$
With the power of `FixedPointChip`, it's easy to implement these formulas to support the inferences of linear and logistic regression.
As for the training, although they are convex functions under a given loss (e.g., mean square error, log loss), the closed solution involves some numerical unstable operations such as matrix inverse operation which has the ill-conditioned problem. So I decide to implement the training with SGD algorithm. SDG will iteratively update the model parameters by the gradient of the loss function to approach the global optimal solution. The SGD algorithm is (original source from [7]):

### ZK-DT: DecisionTreeChip
* Inference: tree traversal with path padding
* Train (CART algorithm)
* Calculate Gini impurity for a given split param in each node
* GetSplit: select the perfect split w/ min Gini in each node
* Transform recursion with Queue & fake nodes
<img src="https://raw.githubusercontent.com/DCMMC/ZKFixedPointChip/main/figure/decision_tree_inference.png" width="80%">
The inference of decision tree involves tree traversal in the decision tree. The traversal path is from root node to leaf node. In each non-leaf node, the node will select left or right branch according to the conditional expression (e.g., $x_0 < 1.3$) in the node. Because for different input, the traversal path is different and the length of the path is also different. But variable length input is unfriendly to ZK circuit. To solve this problem, I propose to use path padding to force all traversal paths to have the same length. For example, we have two paths in the above figure. Path 1 has length of 3 and Path 2 has length of 2. Because the maximum length of all possible paths is 3. So all the traversal paths will be padding into length of 3. For path 2, although the second node is the leaf node. But to make the path padded into length of 3, `DecisionTreeChip` will add one self-loop for this leaf node and repeat accessing this leaf node once. To represent the decision tree with a ZK friendly structure, each node in decision tree is represented with a $5$-tuple: $\langle \text{slot, val, LR, RT, CLS} \rangle$ where slot denotes the split feature argument for this node, val is the split value, LR is the index of left child node, RT is the index of right child, and CLS is the class of this node. If the current node is leaf node, then slot, val are both $0$, and LR and RT are just the index of the current node which will bring self-loop for leaf nodes. If the current node is non-leaf node, then CLS will be a special fake class $255$.
To train the decision tree, we need to recursively generate the deicion tree from top node to bottom. In each non-leaf node, we will calculate Gini impurities for different split parameters (split feature, split value) and find the best split with minimum Gini impurity. Gini Impurity is the probability of incorrectly classifying a randomly chosen element in the dataset if it were randomly labeled according to the class distribution in the dataset. A perfect splitting results in a Gini score of $0$, whereas the worst case split that results in a Gini score of $0.5$ (for a binary class problem). The formula of Gini impurity is $G = \sum_{i=1}^C p(i) \times (1-p(i))$ where $p(i)$ is the probability of randomly picking an element of class $i$. To find the best split in each node, it will first calculates Gini impurities for different split parameters over the dataset in this node. The best split has the minimum Gini impurity. Each non-leaf node has a conditional expression to decide the next node is either the left child or the right child. And the dataset of current node will be splitted into left part and right part according to the conditional expression. The left part of dataset will be the dataset used in the left child node. The right part of dataset will be the one used in the right child node. The conditional expression consists of the split feature and the split value. Because the dataset contains multiple samples and each sample has many features, the conditional expression is something like $x_0 < 1.3$ where the split feature is the first feature in the dataset and the split value is $1.3$. The conditional expression is used to determine whether each sample in the dataset goes to the left part or the right part. The criteria to decide whether the node is leaf node is controled by hyper-parameter `min_size` and the depth of the generated decision tree is controled by `max_depth`. If the number of samples in the dataset of the current node is less than or equal to `min_size`, then the current node will be leaf node and the class of this node is the most common class in the dataset of current node. Because the training process is recursion but the recursion is ZK unfriendly, in the implementation, the recursions will be transformed into non-recursion using queue. And decision tree is not ensured to always be complete binary tree. Non-complete binary tree will leads to variable length of input and computation steps which is not supported by ZK circuit. This project proposes fake node to eliminate this obstacle. As shown in the above figure, the blue dashed circles are fake nodes. During training, we will still do the split even for the leaf node and the added child nodes for the leaf node are called fake nodes. Fake nodes do not influence the result because we have added the self-loop for the real leaf node (yellow circles).
## 0x3 Future Directions
### Replacing `select_from_idx` with `lookup` tables in ZK-LR and ZK-DT
The training of ML algorithms will involve a large amount of data samples. Current implementation utilizes `select_from_idx` provided by Axiom's `halo2-base` to get a specific sample in a given dataset with index. You can treat it as accessing an element from an array by index. The implementatiom of `select_from_idx` will decompose the index into an one-hot vector whose length is same as the target array and then uses inner product to get the element. Because the dataset is fixed during the whole training and there are a large amount of accessing operations, it's sub-optimal to do so many inner products for the same dataset. `lookup` table is an important feature of `halo2` and a better alternative of `select_from_idx`.
### Reducing cells and computations in FixedPointChip
The performance of the current implementation still has a lot of room for improvement. For example, the current `inner_product` just calculates the element-wise production for each pair and then sum them. It is expected to be improved with gate overlapping like the implementation in Axiom's `halo2-base`. Improving `FixedPointChip` should be a core direction in the future.
### Packing multiple numbers inside one BN254 variable
As an advice by Horace Pan et al.'s ZKML project [10], the extra capacity of BN254 variables will be wasted for `FixedPointChip` with low-precision. Packing multiple numbers inside one BN254 variable is one solution to improve the efficiency.
### Fused quantization for combination of multi ML layers (e.g., Linear + ReLU)
In ML scenario, it's common to link multiple computation layers (e.g., `Conv2D-BatchNorm-ReLU`). If we do quantizations on them separately, it will cause some unnecessary redundant computations. It's better to fuse the quantization of commonly used combination of multiple ML layers. This is called fused quantization, as details shown in Lei Mao's blog [1].
## Acknowledgments
This project was conducted in [Axiom Open Source Program](https://www.axiom.xyz/open-source). It is also supported by [Clique2046](https://clique.social/). It's build on top of ZK circuit primitives provided by [Halo2](https://github.com/privacy-scaling-explorations/halo2.git) and Axiom's [Halo2-base](https://github.com/axiom-crypto/halo2-lib). During design and implementation, I also refered many open source projects such as [3] and [6]. Without the infrastructure and help of these projects, this project could not have been born.
## Reference
- [1] Quantization for Neural Networks. 2020. https://leimao.github.io/article/Neural-Networks-Quantization/
- [2] https://machinelearningmastery.com/implement-decision-tree-algorithm-scratch-python/
- [3] https://github.com/XMunkki/FixPointCS/
- [4] https://github.com/abdk-consulting/abdk-libraries-solidity
- [5] I-BERT: Integer-only BERT Quantization. ICML (oral). 2021
- [6] Rust’s official port of MUSL's libm. https://docs.rs/libm/latest/src/libm/math/log.rs.html
- [7] Ian Goodfellow, et al. Deep Learning. pp 290 - 292.
- [8] Leo Breiman, et al. Classification and regression trees. 1984
- [9] https://medium.com/@danieldkang/empowering-users-to-verify-twitters-algorithmic-integrity-with-zkml-65e56d0e9dd9
- [10] ZK Machine Learning. https://hackmd.io/Y7Y79_MtSoKdHNAEfZRXUg
 Sign in with Wallet
Sign in with Wallet

