# Leetcode刷題學習筆記 -- Prefix Sum
### Intrudoction
把前面的數字都加起來稱為prefix sum。可以用來解區段和的問題。

### prefix sum for 1D Array
最簡單的應用就是用$O(1)$算出某個subarray的和。
```cpp
vector<int> nums;
// 使用STL來計算prefix sum
partial_sum(begin(nums), end(nums), begin(nums));
// 或是使用for loop
for(int i = 1; i < nums.size(); ++i)
nums[i] += nums[i - 1];
```
計算出prefix sum之後,就可以用start和end來求subarray sum。
```cpp
// 求出 index = 2 ~ 5之間的subarray sum
cout << nums[5] - nums[1] << endl;
```
### 使用unordered_map/set來記錄走訪過的prefix sum
通常題目會要求符合某個條件的subarray sum。例如:求出subarray sum = K 的subarray個數。
使用unordered_set/map來記錄prefix sum的大小和個數,就可以用$O(1)$來查詢之前的pfx數值。 參考 [560. Subarray Sum Equals K(Medium)](https://hackmd.io/Io-i2knhQvaqqXSOKn2BcA?both#560-Subarray-Sum-Equals-KMedium)
因為會往前尋找prefix sum,所以必須把0提前加入map或是set中。
因為0的意思是從第0個到目前的subarray sum。
```cpp
unordered_map<int, int> m{{0, 1}};
unordered_set<int> s{{0}};
```
### Downside and time complexity
| | Time Complexity | Note |
| --------- | --------------- | ------------------------------------------- |
| initial | $O(N)$ | 必須走訪全部的element來建立prefix sum array |
| getSum | $O(1)$ | 只需要計算pfs[end] - pfs[start - 1] |
| update | $O(N)$ | 如果一個數值變了必須update之後所有的pfs |
如果使用 ==[BIT(Binary index tree)](/ogxY5ToqTT-RAZUqRhxbgw)== 就可以達到getSum和update都是$O(logN)$
### prefix sum for 2D Array
求出綠色/藍色或是紅色框出來的sum。
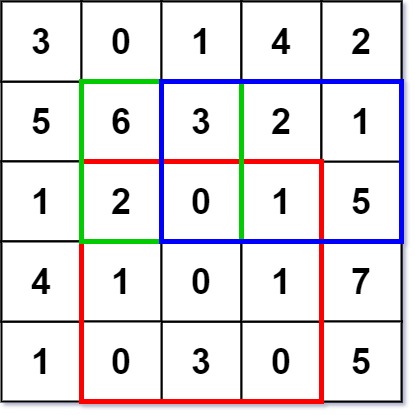
計算2D prefix array,其中pfs[y][x]為起點是(0, 0)到(y, x)的sum。
```cpp
vector<vector<int>> nums;
int m = nums.size();
int n = nums[0].size();
// 為了配合計算方便,使用大一點的vector
vector<vector<int>> pfs(m + 1, vector<int>(n + 1));
for(int y = 1; y <= m; ++y) {
for(int x = 1; x <= n; ++x) {
pfs[y][x] = pfs[y - 1][x] + pfs[y][x - 1] + matrix[y - 1][x - 1] - pfs[y - 1][x - 1];
}
}
```
計算某個範圍內的sum
```cpp
int sumRegion(int row1, int col1, int row2, int col2) {
return pfs[row2 + 1][col2 + 1] -
pfs[row2 + 1][col1] -
pfs[row1][col2 + 1] +
pfs[row1][col1];
}
```
### 另一種prefix sum for 2D vector
1. 先針對row做prefix sum
```cpp
vector<vector<int>> nums;
for(auto& row : nums)
partial_sum(begin(row), end(row), begin(row));
```
2. 定義left和right
因為2D的range sum是由(top, left) -> (bottom, right)似的值所組成,所以先決定left和right
```cpp
int m = nums.size();
int n = nums[0].siez();
for(int left = 0; left < n; ++left) {
for(int right = left; right < n; ++right) {
}
}
```
3. 計算每個row從left到right的range sum
下面是計算(y, left) -> (y, right)
```cpp
nums[y][right] - (left - 1 >= 0 ? nums[y][left - 1] : 0);
```
4. 計算縱向的perfix sum
```cpp
int pfs = 0;
for(int y = 0; y < m; ++y) {
pfs += nums[y][right] -
(left - 1 >= 0 ? nums[y][left - 1] : 0);
}
```
5. 根據題目需求使用unordered_set/map或是set/map。
參考
+ [1074. Number of Submatrices That Sum to Target](https://hackmd.io/Io-i2knhQvaqqXSOKn2BcA#1074-Number-of-Submatrices-That-Sum-to-Target)
+ [363. Max Sum of Rectangle No Larger Than K](https://hackmd.io/Io-i2knhQvaqqXSOKn2BcA#363-Max-Sum-of-Rectangle-No-Larger-Than-K)
#### [560. Subarray Sum Equals K(Medium)](https://leetcode.com/problems/subarray-sum-equals-k/)
給你一個vector<int> nums,求出subarray的和是k的個數。
> 1. 一開始我是使用dp的方法,dp[i][j],其中i代表開始,j代表結束,dp[i][j] = dp[i][j - 1] + nums[j]。但是這個方法會timeout。因為為O(N^2)。
> 2. 使用prefix sum,解法如下,也是會timeout。因為還是O(N^2)的演算法。
```cpp=
int subarraySum(vector<int>& nums, int k) {
int n = nums.size(), rtn{0};
vector<int> sum(n + 1, 0);
sum[1] = nums[0];
for(int i = 2; i <= n; ++i)
sum[i] = nums[i - 1] + sum[i - 1];
for(int i = 1; i <= n; ++i) {
for(int j = i; j <= n; ++j) {
if(sum[j] - sum[i - 1] == k) rtn++;
}
}
return rtn;
}
```
> 3. 如下圖,當index走到i的時候,把這邊當終點,往前回推n個如果和是k,那這個subarray就是一個解。n前面的和即為sum - k。用一個hashmap紀錄prefix sum的個數,就可以達到O(N)。

```cpp=
int subarraySum(vector<int>& nums, int k) {
int n = nums.size(), rtn{0}, sum{0};
unordered_map<int, int> m{{0, 1}}; //self
for(auto& n : nums) {
sum += n;
rtn += m[sum - k];
m[sum]++;
}
return rtn;
}
```
### 對sorted array做prefix sum
#### [1508. Range Sum of Sorted Subarray Sums](https://leetcode.com/problems/range-sum-of-sorted-subarray-sums/)
> 1. 題目是對sorted array做prefix sum,然後要找出排序後從left到right的總和。
> 2. 因為是sorted array所以出現的subarray sum從小到大的順序可以預測。
```cpp
// 這題的題目是對"sorted array" 做處理。 因為是sorted array[1, 2, 3, 4]
// 從1開始的subarray : [1], [1, 2], [1, 2, 3], [1, 2, 3, 4] ==> subarray sum = [1, 3, 6, 10]
// 從2開始的subarrry : [2], [2, 3], [2, 3, 4] ==> subarray sum = [2, 5, 9]
// 從3開始的subarray : [3], [3, 4] ==> subarray sum = [3, 7]
// 從4開始的subarray : [4] ==> subarray sum = [4]
int rangeSum(vector<int>& nums, int n, int left, int right) {
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
for(int i = 0; i < n; ++i)
pq.push({nums[i], i + 1}); // 每一個數字開頭的subarray,長度只有1
int ans = 0, m = 1e9 + 7;
for(int i = 1; i <= right; ++i) {
auto p = pq.top(); pq.pop(); // 先取出最小的
if(i >= left)
ans = (ans + p.first) % m;
if(p.second < n) { // 加上下一個數字,例如 : [2, 3] --> [2, 3, 4], 長度 + 1
p.first += nums[p.second++];
pq.push(p);
}
}
return ans;
}
```
### 將Array轉換為正負值,求prefix sum。
有的題目必須將array轉換為正負值,這樣比較方便比較兩種不同性質的element。
+ 通常是求subarray或是interval的題目。也就是連續數值。
+ 可以將數值分成兩種特性(+1/-1)
#### [1124. Longest Well-Performing Interval](https://leetcode.com/problems/longest-well-performing-interval/description/)
題目是說數值大於8的為tiring day, well-performing interval定義為某個interval中tiring day的日子大於non-tiring day的日子。
> 1. 將大於8的數值定義為1, 小於等於8的數值為-1。
> 2. 使用prefix sum
> 3. 一開始我是使用以下的code,從最開始找,直到sum - 1。
```cpp=
map<int, int> m;
for(auto it = m.begin(); it->first <= sum - 1; ++it) {
ans = max(ans, i - it->second);
}
```
> 4. 因為我們只儲存第一個出現的index,越接近0的數值越早出現。所以我們只要檢查sum - 1即可。參考[這邊的解說](https://leetcode.com/problems/longest-well-performing-interval/solutions/334565/java-c-python-o-n-solution-life-needs-996-and-669/)。
```cpp=
int longestWPI(vector<int>& hours) {
int ans = 0, sum = 0;
unordered_map<int, int> m;//value, index
m[0] = -1;
for(int i = 0; i < hours.size(); ++i) {
sum += hours[i] > 8 ? 1 : -1;
if(sum > 0) ans = max(ans, i + 1); // 因為大於0就是全部的長度是最長的
else {
if(m.count(sum - 1)) ans = max(ans, i - m[sum - 1]);
if(!m.count(sum)) m[sum] = i;
}
}
return ans;
}
// 這種問題都是從0開始
// 6, 6, 6, 9, 6, 9, 9
// 0|x
// -1| x x
// -2| x x x
// -3| x x
// 最後一個9, sum = -1, 可以找到符合的有-2, -3
// 因為我們都只存最前面的-2,而且要到-3,必須先經過-2,
// 所以-2永遠會比-3還前面,所以不用檢查小於-2的數值。
// 也就是我們只儲存第一個數值,所以越接近0的數值一定越早出現。
```
#### [525. Contiguous Array](https://leetcode.com/problems/contiguous-array/)
給你一個binary array,找出1和0數目一樣的最長subarray。
```cpp=
class Solution {
//[ 0, 0, 1, 1, 1, 0]
//[-1, -2, -1, 0, 1, 0]
// ------
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int, int> m; // value, index
m[0] = -1; // 因為也是prefix sum的概念,所以必須加上開頭
int balance{0}, ans{0};
for(int i = 0; i < nums.size(); ++i) {
balance += nums[i] ? 1 : -1;
if(m.count(balance)) ans = max(ans, i - m[balance]);
else m[balance] = i;
}
// time : O(N)
// space : O(N)
return ans;
}
};
```
## Problems
### [1658. Minimum Operations to Reduce X to Zero](https://leetcode.com/problems/minimum-operations-to-reduce-x-to-zero/)
一開始看到了minimum operrations,就使用了DP結果TLE。看了hints,因為只能從最左和最右刪除,所以最後只會剩下subarray,所以問題就可變成找出最長的subarray,則sz - subarray.size() 就會是minimal operations。
下面的解法是用prefix sum + hash table。
time complexity : $O(N)$
space complexity : $O(N)$
```cpp=
int minOperations(vector<int>& nums, int x) {
int sz = nums.size();
int total = accumulate(nums.begin(), nums.end(), 0);
if(x > total) return -1;
if(x == total) return sz;
int target = total - x;
unordered_map<int, int> m;
m[0] = -1;
int sum = 0, maxlen = 0;
for(int i = 0; i < sz; ++i) {
sum += nums[i];
if(sum >= target && m.count(sum - target))
maxlen = max(maxlen, i - m[sum - target]);
m[sum] = i;
}
return maxlen > 0 ? sz - maxlen : -1;
}
```
### [1074. Number of Submatrices That Sum to Target](https://leetcode.com/problems/number-of-submatrices-that-sum-to-target/)
給你一個2D Array求出,subarray的和為target的個數。
> 1. 一開始使用 2D array算prefix的做法,但是time complexity非常差。
```cpp=
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
int rtn = 0;
for(int y = 0; y < m; ++y) { // bottom
for(int x = 0; x < n; ++x) { // right
dp[y + 1][x + 1] = dp[y][x + 1] + dp[y + 1][x] - dp[y][x] + matrix[y][x];
for(int i = 0; i <= y; ++i) { // top
for(int j = 0; j <= x; ++j) { //left
if(dp[y + 1][x + 1] - dp[i][x + 1] - dp[y + 1][j] + dp[i][j] == target) rtn++;
}
}
}
}
// time : O(MN * MN)
// space : O((MN))
return rtn;
}
```
> 1. 這題是[560. Subarray Sum Equals K(Medium)](https://hackmd.io/Io-i2knhQvaqqXSOKn2BcA?both#560-Subarray-Sum-Equals-KMedium)變成2D版本。
> 2. 所以問題可以變成怎麼把2D版本變成1D版本。
> 3. 先對row做prefix sum
> 4. 再掃描left和right找出,符合條件的個數。
```cpp=
int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) {
int m = matrix.size();
int n = matrix[0].size();
for(int i = 0; i < m; ++i)
partial_sum(matrix[i].begin(), matrix[i].end(), matrix[i].begin()); // O(MN)
unordered_map<int, int> counter; // prefix sum, count
int ans = 0;
for(int left = 0; left < n; ++left) {
for(int right = left; right < n; ++right) {
counter = {{0, 1}}; // clear map and add only one item
int pfs = 0;
for(int k = 0; k < m; ++k) {
pfs += matrix[k][right] - (left - 1 >= 0 ? matrix[k][left - 1] : 0);
ans += counter[pfs - target];
counter[pfs]++;
}
}
}
// time : O(MN + MNM) = O(MNM)
// psace : O(MN)
return ans;
}
```
### [363. Max Sum of Rectangle No Larger Than K](https://leetcode.com/problems/max-sum-of-rectangle-no-larger-than-k/)
```cpp
int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {
for(auto& row : matrix)
partial_sum(begin(row), end(row), begin(row));
int m = matrix.size();
int n = matrix[0].size();
int ans = INT_MIN;
for(int left = 0; left < n; ++left) {
for(int right = left; right < n; ++right) {
int pfs = 0;
set<int> s{0};
for(int y = 0; y < m; ++y) {
pfs += matrix[y][right] - (left - 1 >= 0 ? matrix[y][left - 1] : 0);
auto it = s.lower_bound(pfs - k);
if(it != s.end()) ans = max(ans, pfs - *it);
s.insert(pfs);
}
}
}
return ans;
}
```
### [523. Continuous Subarray Sum](https://leetcode.com/problems/continuous-subarray-sum/)
給你一個vector<int>和k,找出subarray sum為k的倍數。且長度至少為2。
> 1. 一開到subarray sum就想到使用prefix sum
> 2. 如果只是求剛好等於k的話,那就是查詢遇到的prefix sum始有否k - cur_pfs。
> 3. 但是這邊是要k的倍數。k的倍數意味著,0, k, 2*k, 3*k, ...
假設從第i個到第j個的subarry sum為k的倍數。
pfs(j) - pfs(i - 1) = m * k
兩邊各取mod k,則 pfs(j) % k - pfs(i - 1) % k = 0
=> pfs(j) % k = pfs(i - 1) % k
把prefix sum用mod K存起來,只要遇到和目前prefix sum mod k 相同的值,即為我們要的。
> 4. 因為長度最少要2以上,所以對相同的prefix sum來說,我們只需要儲存index最小的那一個,因為這樣可以保證長度是最長的。
```cpp
bool checkSubarraySum(vector<int>& nums, int k) {
if(k == 1) return nums.size() >= 2;
// 因為只要知道最小index的prefix sum(4)
unordered_map<int, int> m{{0, -1}}; // prefix sum, minamum idx
int pfs{0};
for(int i = 0; i < nums.size(); ++i) {
pfs = (pfs + nums[i]) % k;
if(m.count(pfs) && i - m[pfs] >= 2) return true;
if(!m.count(pfs)) m[pfs] = i;
}
return false;
}
```
### [974. Subarray Sums Divisible by K](https://leetcode.com/problems/subarray-sums-divisible-by-k/description/)
給你一個vector<int>和K,找出subarray的個數使得subarray sum為可以被K整除。這邊數值會有負數。
> 1. 因為subarray sum所以使用prefix sum
> 2. 統計prefix sum出現的個數,就可以計算符合條件的subarray個數。
> 3. 因為要可以整除K,所以觀念和[523. Continuous Subarray Sum](/Io-i2knhQvaqqXSOKn2BcA#523-Continuous-Subarray-Sum)一樣。
pfs(cur) - pfs(prev) = m * K
pfs(cur) % K = pfs(prev) % K
> 4. 可是這邊有負數!! 參考[負數mod](https://hackmd.io/3I17t2spT6GDLFRftfEOZA?view#mod)
因為 -1 % 3 = -2
所以使用 (n%k + k) % k,因為n為正整數結果不變。
如果是負數,則 -1 % 3 = -1。 (-1 + 3) % 3 = 2。
(1 + (-1) % 3 + 3) % 3 = 0,才是我們要的結果。
```cpp
int subarraysDivByK(vector<int>& nums, int k) {
unordered_map<int, int> m{{0, 1}}; //prefix sum % k, count
int pfs{0}, ans{0};
for(auto& n : nums) {
pfs = (pfs + n % k + k) % k;
// pfs(cur) - pfs(prev) = m * k
// pfs(cur) % k = pfs(prev) % k
// 因為n 有可能為negative, 所以必須用 n % k + k
ans += m[pfs];
m[pfs]++;
}
return ans;
}
```
### [862. Shortest Subarray with Sum at Least K](https://leetcode.com/problems/shortest-subarray-with-sum-at-least-k/description/)
給你一個vector<int>和K,求出subarray sum最少為K,返回最短的長度,如果沒有則返回-1。
> 1. 看到subarray sum那就是使用 prefix sum
> 2. 因為是最短的長度,所以和[523. Continuous Subarray Sum](/Io-i2knhQvaqqXSOKn2BcA#523-Continuous-Subarray-Sum)相反,當prefix sum一樣的時候,只要存最大index就可以。這樣長度才會最短。
> 3. 另外使用long避免prefix sum加到overflow。
> 4. 因為是subarray sum最少為k,
pfs(cur) - pfs(prev) >= k, i < j
pfs(prev) <= pfs(cur) - k
必須嘗試所有比pfs(cur) - k還小的值。
> 5. 所以使用upper_bound找出 > pfs(cur) - k的值,然後從前一個開始嘗試。
> 6. 最後把現在的pfs插入到map中,因為插入的index一定是最大值,所以把比目前的pfs還大的都刪除掉。
> 7. 因為保留了最大index的pfs所以(5)不用全部都試,只需要試前upper_bound的前一個即可。
```cpp
int shortestSubarray(vector<int>& nums, int k) {
int sz = nums.size();
map<long, int> m{{0, -1}}; //prefix sum, maximum index
int minans = sz + 1;
long pfs{0};
for(int i = 0; i < nums.size(); ++i) {
pfs += nums[i];
auto it = m.upper_bound(pfs - k);
if(it != m.begin()) {
it = prev(it, 1);
minans = min(minans, i - it->second);
}
m[pfs] = i;
while(m.rbegin()->first != pfs)
m.erase(m.rbegin()->first);
}
return minans == sz + 1 ? -1 : minans;
}
```
###### tags: `leetcode` `刷題`
 Sign in with Wallet
Sign in with Wallet

