## What we want out of STARK signature aggregation

Today, Ethereum's beacon chain relies on BLS aggregation to aggregate a large number of signatures into a single combined aggregate:

<center><br>


</center><br>

The aggregate contains a single fixed-size elliptic curve point (96 bytes), plus a bitfield specifying which of the allowed participants actually participated (1 bit per participant). Verifying the aggregate requires computing the group public key: 1 ECADD per participant.

To avoid requiring one node to process 96 * N bytes of bandwidth (because N can be very large, potentially hundreds of thousands), in practice we do two-level aggregation, where signatures from subsets of validators get aggregated separately and the agggregates of the subsets go into the main p2p network:

<center><br>


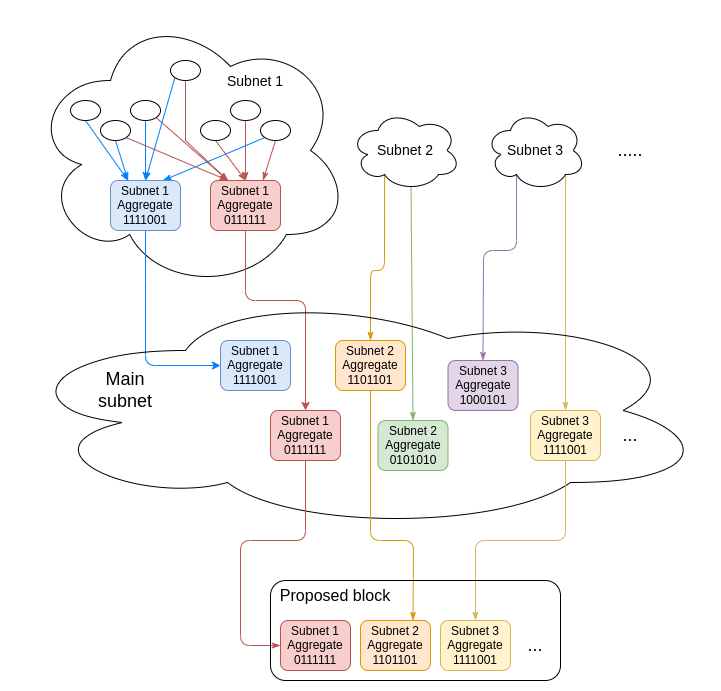
</center><br>

However, this is not quantum-proof, and it's not very SNARK-friendly, because we end up having to do N BLS12-381 curve additions inside a SNARK (which would have to be done in mismatched-field arithmetic unless a particular curve is chosen for the SNARK). Hence, we want a hash and STARK-based equivalent to this design.

## What might this look like?

We will assume that signatures use some hash-based signature, perhaps some Winternitz variant, where the pubkeys are 32 bytes long (we can make any signature scheme have a 32-byte pubkey by replacing the pubkey with a hash of the pubkey, and adding the original pubkey to the signature). We want to aggregate many of these signatures into an object that we will assume is made up of a bitfield plus a STARK proof.

One possible approach is to create a STARK circuit for the aggregation problem in general:

* **Public inputs**: N pubkeys, message hash $m$
* **Private inputs**: N signatures
* **Statement**: For all $1 \le 1 \le N$, the $i$'th signature is a valid signature of $m$ with the $i$'th pubkey

The verifier would determine which pubkeys to introduce as public inputs from the bitfield in the aggregate. Alternatively, the public inputs could include some kind of a root hash of the list of _all_ pubkeys and a bitfield; then, extraction of the individual pubkeys could be inside the STARK.

However, this is not feasible in practice, because it would require a single actor to STARK over many thousands of signatures, each of which contain thousands of hashes.

A better approach is a recursive route, where aggregation happens in multiple layers. Each layer unions the aggregates coming in. This allows the network to be highly unstructured:

<center><br>


</center><br>

In this case, the statement being proven would be something like:

* **Public inputs**: Root of all pubkeys $R$, bitfield, message hash $m$
* **Private inputs**: N STARKs with N bitfields, and M signatures with M participant indices
* **Statement**:
* For all $1 \le i \le N$, the $i$'th provided STARK is a valid STARK of this statement using the $i$'th bitfield as the public bitfield input and the same $R$ and $m$
* For all $1 \le i \le M$, the $i$'th provided signature is a valid signature of $m$ with the pubkey at the position defined by the $i$'th participant index in the pubkeys tree rooted in $R$
* The public bitfield is the union of all the bitfields in the STARKs, with 1s filled in for each of the $m$ indices for which we have individual signatures

Notice the recursion ("... is a valid STARK of _this statement_ using..."); this is the most challenging part of implementing this proof.

The key question to determine is how long it takes to prove this statement with some fixed width (eg. $N + M \le 8$). If we can prove such a statement in under ~250 ms, then we could rely on a highly unstructured network with degree $\le 8$ to aggregate even a very large number of signatures within a few seconds, and this would probably be sufficient to solve the aggregation problem.