# 2020q3 Homework (quiz5)
contributed by < `hankluo6` >
### 測驗 1
```c
#include <stdio.h>
#include <stdlib.h>
double divop(double orig, int slots) {
if (slots == 1 || orig == 0)
return orig;
int od = slots & 1;
double result = divop(orig / D1, od ? (slots + D2) >> 1 : slots >> 1);
if (od)
result += divop(result, slots);
return result;
}
```
:::warning
選項不用保留,原題目已有。你該專注探討你的思路和延伸討論
:notes: jserv
:::
:::info
已更改!
:::
#### `D1`
- [x] `(c)` `2`
#### `D2`
- [x] `(d)` `1`
#### 延伸問題
1. 解釋上述程式碼運作原理;
分數可以透過拆解來計算,分成兩種 Case:
* 分母為偶數
當分母為偶數時,表示此分數必定能用有限小數表示,所以將分子分母同除 2 不會影響答案精度。
* 分母為奇數
當分母為奇數時,此分數**不一定**能表示成有限小數(分子分母有公因數才能),但可以將分數透過以下公式拆解:
$$
\begin{align}
\frac{y}{x} &= \frac{y}{x}\times\frac{x+1}{x+1}\\
&= \frac{1}{x} \times \frac{xy+y}{2} \times \frac{2}{x+1} \\
&= \frac{y}{2}\times\frac{2}{x+1}+\frac{y}{2}\times \frac{2}{x+1}\times\frac{1}{x} \\
&= \frac{y/2}{(x+1)/2}+\frac{y/2}{(x+1)/2}/x
\end{align}
$$
此公式第一個 term 為偶數,而第二個 term 則為奇數,但分子比原本的分數還小,只要持續遞迴下去,就能保證 Condition `if (slots == 1 || orig == 0)` 會成立。第二個 term 在算的其實就是分數精度,持續計算直到超出 floating point 的上限為止。
程式會先判對奇偶數並將結果放置在 `od` 中,因不管奇偶數,都需將分子除 2,所以可以保證程式最後會終止。根據上面的推導,`D1` 與 `D2` 自然就知道了。
2. 以編譯器最佳化的角度,推測上述程式碼是否可透過 [tail call optimization](https://en.wikipedia.org/wiki/Tail_call) 進行最佳化,搭配對應的實驗;
* 搭配閱讀 [C 語言: 編譯器和最佳化原理](https://hackmd.io/@sysprog/c-compiler-optimization?type=view) 及 [C 語言: 遞迴呼叫](https://hackmd.io/@sysprog/c-recursion?type=view)
推測此程式第一個遞迴函式能透過 TCO 最佳化,而第二個不能,因程式最後不為 function call,而是 `result` 的加法動作。
透過 `gcc -S -O3` 分析編譯後的組合語言
```
divop:
.LFB39:
...
testb $1, %dil
jne .L3
.L4:
mulsd %xmm2, %xmm0
sarl %ebp
cmpl $1, %ebp
sete %dl
je .L1
ucomisd %xmm1, %xmm0
setnp %al
cmovne %edx, %eax
testb %al, %al
jne .L1
testb $1, %bpl
je .L4
.L3:
mulsd %xmm2, %xmm0
leal 1(%rbp), %edi
sarl %edi
call divop
movl %ebp, %edi
movsd %xmm0, 8(%rsp)
call divop
movsd 8(%rsp), %xmm1
addsd %xmm1, %xmm0
.L1:
...
.L12:
.cfi_restore 6
ret
.cfi_endproc
```
前面 `.LFB39` 處理 `if` 的部份,會先判斷 `od` 是否為 1,並根據結果跳到 `.L4` 或 `.L3`。
在 `od` 非 1 時會進入 `.L4`,從程式碼中可以看到,因底下 `if` 不會進入,故此部份應可以用 tail call optimization 優化,在 assembly language 中能發現沒有使用到 `call` 指令,而是用 `je .L4` 來遞迴,符合我們的推測。
在 `od` 為 1 時進入 `.L3`,此部份需要計算兩次 `divop` 的結果,且最後要相加回 `result`,故此部份不能優話,在 assembly language 中也能看到呼叫兩次 `call divop`,且最後需要呼叫 `addsd` 指令來做最後的相加。
3. 比照 [浮點數運算和定點數操作](https://hackmd.io/@NwaynhhKTK6joWHmoUxc7Q/H1SVhbETQ),改寫上述程式碼,提出效率更高的實作,同樣避免使用到 FPU 指令 (可用 gcc -S 觀察對應的組合語言輸出),並與使用到 FPU 的實作進行效能比較
假設我們只專注在效能而不是精度上,可以利用 [Fast inverse square root](https://en.wikipedia.org/wiki/Fast_inverse_square_root) 中的原理來計算除數倒數,在乘上被除數來完成除法。
程式碼來自 [Fast 1/X division (reciprocal)](https://stackoverflow.com/questions/9939322/fast-1-x-division-reciprocal):
```c
double my_divop(double orig, int slots) {
union {
double dbl[2];
uint64_t ull[2];
} u;
u.dbl[0] = (double)slots;
u.ull[1] = 0;
u.ull[0] = ( 0xbfcdd6a18f6a6f52ULL - u.ull[0] ) >> 1;
u.dbl[1] = 0;
u.dbl[0] *= u.dbl[0];
return u.dbl[0] * orig;
}
```
還有一點要注意的是,原先題目程式碼會有無窮迴圈的情況發生,原因是因為浮點數在判斷式上會有誤差,故 `orig == 0` 這個判斷式有可能永遠不會成立,可參考 [Why doesn’t my floating-point comparison work?](http://isocpp.org/wiki/faq/newbie#floating-point-arith),將判斷的部份改為 `orig <= 1e-10` 來解決。

因為原程式有用到遞迴操作,時間與其他兩種方法差距相當大。
將其他兩個版本放大:
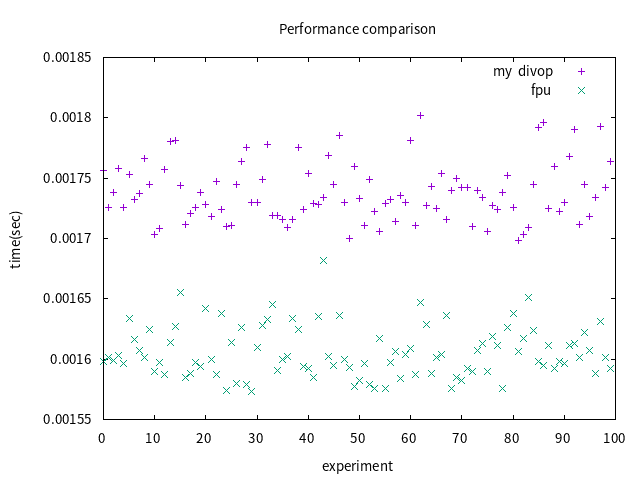
可以發現使用 FPU 的運算效率還是比沒有使用的好,且此實作版本的精確度相當低,故在有 FPU 架構的硬體上還是使用內建除法較好。
---
### 測驗 2
```cpp=
#include <stdint.h>
/* A union allowing us to convert between a float and a 32-bit integers.*/
typedef union {
float value;
uint32_t v_int;
} ieee_float_shape_type;
/* Set a float from a 32 bit int. */
#define INSERT_WORDS(d, ix0) \
do { \
ieee_float_shape_type iw_u; \
iw_u.v_int = (ix0); \
(d) = iw_u.value; \
} while (0)
/* Get a 32 bit int from a float. */
#define EXTRACT_WORDS(ix0, d) \
do { \
ieee_float_shape_type ew_u; \
ew_u.value = (d); \
(ix0) = ew_u.v_int; \
} while (0)
static const float one = 1.0, tiny = 1.0e-30;
float ieee754_sqrt(float x)
{
float z;
int32_t sign = 0x80000000;
uint32_t r;
int32_t ix0, s0, q, m, t, i;
EXTRACT_WORDS(ix0, x);
/* take care of zero */
if (ix0 <= 0) {
if ((ix0 & (~sign)) == 0)
return x; /* sqrt(+-0) = +-0 */
if (ix0 < 0)
return (x - x) / (x - x); /* sqrt(-ve) = sNaN */
}
/* take care of +INF and NaN */
if ((ix0 & 0x7f800000) == 0x7f800000) {
/* sqrt(NaN) = NaN, sqrt(+INF) = +INF,*/
return x;
}
/* normalize x */
m = (ix0 >> 23);
if (m == 0) { /* subnormal x */
for (i = 0; (ix0 & 0x00800000) == 0; i++)
ix0 <<= 1;
m -= i - 1;
}
m -= 127; /* unbias exponent */
ix0 = (ix0 & 0x007fffff) | 0x00800000;
if (m & 1) { /* odd m, double x to make it even */
ix0 += ix0;
}
m >>= 1; /* m = [m/2] */
/* generate sqrt(x) bit by bit */
ix0 += ix0;
q = s0 = 0; /* [q] = sqrt(x) */
r = QQ0; /* r = moving bit from right to left */
while (r != 0) {
t = s0 + r;
if (t <= ix0) {
s0 = t + r;
ix0 -= t;
q += r;
}
ix0 += ix0;
r >>= 1;
}
/* use floating add to find out rounding direction */
if (ix0 != 0) {
z = one - tiny; /* trigger inexact flag */
if (z >= one) {
z = one + tiny;
if (z > one)
q += 2;
else
q += (q & 1);
}
}
ix0 = (q >> 1) + QQ1;
ix0 += (m << QQ2);
INSERT_WORDS(z, ix0);
return z;
}
```
#### `QQ0`
- [x] `(a)` `0x01000000`
#### `QQ1`
- [x] `(d)` `0x3f000000`
#### `QQ2`
- [x] `(g)` `23`
```c=36
/* take care of zero */
if (ix0 <= 0) {
if ((ix0 & (~sign)) == 0)
return x; /* sqrt(+-0) = +-0 */
if (ix0 < 0)
return (x - x) / (x - x); /* sqrt(-ve) = sNaN */
}
```
此部分處理 float 為 0 與 negative 的部分,當為 0 時,回傳 0,為負數時回傳 NaN。
```c=43
/* take care of +INF and NaN */
if ((ix0 & 0x7f800000) == 0x7f800000) {
/* sqrt(NaN) = NaN, sqrt(+INF) = +INF,*/
return x;
}
```
當 exponent 部分全為 1 時為 [IEEE 754](https://en.wikipedia.org/wiki/IEEE_754) 定義的特殊值,回傳原本數字。
```c=48
/* normalize x */
m = (ix0 >> 23);
if (m == 0) { /* subnormal x */
for (i = 0; (ix0 & 0x00800000) == 0; i++)
ix0 <<= 1;
m -= i - 1;
}
```
接著先計算 exponent 部分,`(ix0 >> 23)` 取得 exponent 的值,如果為 0,表示為 [subnormal number](https://en.wikipedia.org/wiki/Denormal_number),
```c=55
/* normalize x */
m -= 127; /* unbias exponent */
ix0 = (ix0 & 0x007fffff) | 0x00800000;
if (m & 1) { /* odd m, double x to make it even */
ix0 += ix0;
}
m >>= 1; /* m = [m/2] */
```
將數值 normalize,將 exponent 轉為真正的指數,並用 `ix0` 紀錄 normalize 後的有效數部分。
:::warning
這邊有效數(亦稱尾數)指的是轉換為科學記號後 $a \times 2^n$ 中 $a$ 的部分,須滿足 $1 \leq a < 2$,與 IEEE 754 中 mantissa 的意義稍有不同。
:::
因開根號為 $\frac{1}{2}$ 次方,相當於指數部分除 2,故底下 `m >> 1` 用來對指數部分開根號,特別注意當指數次方為奇數時,會將指數的一次方移到有效數,讓指數形成偶數能整除。
故現在有兩種情形:
* $x = a \times 2^n \quad 0 \leq a < 2 \quad \text{if } n \text{ is even}$
* $x = a \times 2^{n-1}\quad 0 \leq a < 4 \quad \text{if } n \text{ is odd}$
接著為計算 square root 的部分,詳細演算法可以參考 [How to calculate a square root without a calculator](https://www.homeschoolmath.net/teaching/square-root-algorithm.php) 或 [Wikipedia](https://en.wikipedia.org/wiki/Methods_of_computing_square_roots#Binary_numeral_system_(base_2)),利用每次選擇次方最接近目標數值的值,來漸漸逼近目標數值。演算法的證明可以從 [Why the square root algorithm works](https://www.homeschoolmath.net/teaching/sqr-algorithm-why-works.php) 來理解。
寫成流程圖方便理解:
```flow
st=>start
e=>end:>http://www.google.com
op1=>operation: Let r be the maximum value of ix0
op2=>operation: Initialize s0 and q to zero
op3=>operation: ix0 -= (s0 + 2r),
q += r, s0 += 2r
op4=>operation: ix0 <<= 1,
r >>= 1
cond1=>condition: ix0 >=
s0 + r
cond2=>condition: r == 0 ?
st->op1->op2->cond1
cond1(yes)->op3(right)->op4->cond2(yes)->e
cond2(no)->cond1
cond1(no)->op4
```
網路上有很多此直式除法開根號的例子,故這邊主要討論一般直式開根號方法與程式間的差異:
* 直式中的除數可以直接從高位元上運算,而在程式中使用的是真正處理位元上的位置,所以用 `r` 表示當前處理位置
* 直式中有將除數位移的步驟,在程式中因除數為真正位元的位置,故移動 `r` 的位置就能形成位移除數的效果
* 直式中有除數乘 2 的部分,而在程式中除數補 0 後位移的步驟可省略 (因為處理的為真正的位元,0 不影響除數),使用加兩次 `r` 與暫存變數來方便運算
* 直式中一次處理兩個數字,等價於程式中同時位移 `ix0` 與 `r`
從例子來觀察:
```
1 0 0 1 1 0 0 1
shift and add 1 --------- shift r and add r ---------
√ 1010001 √ 1010001
1 1 01000000 1000000
--------- ---------
101 01 10100000 100010 shift ix0
0 0
--------- ---------
1001 100 10010000 1000100 shift ix0
0 0
--------- ---------
10001 10001 10001000 10001000 shift ix0
10001 10001000
-------- ---------
0 0
Normal Version Program Version
```
在程式中,只有當估測的值(目前商數)與除數相乘小於被除數時,才會將進行處裡位元乘 2 的步驟。
```c=62
/* generate sqrt(x) bit by bit */
ix0 += ix0;
q = s0 = 0; /* [q] = sqrt(x) */
r = QQ0; /* r = moving bit from right to left */
```
`r` 用來檢查被除數位置上的 bit,故必須要比被除數的位元數還要大。57 行將 `ix0` 設定為 24 bit,59 行與 63 行各自位移 1 bit。所以 `ix0` 最高可能為 26 bit 的數字,`r` 必須要比 `ix0` 大且只有一位元為 1,所以答案為 `0x01000000`。
```c=67
while (r != 0) {
t = s0 + r;
if (t <= ix0) {
s0 = t + r;
ix0 -= t;
q += r;
}
ix0 += ix0;
r >>= 1;
}
```
`while` 部分執行下列行為:
1. 透過變數 `t` 決定猜測的商數之目前的 bit 為 1 或 0
* 為 1 則將被處理的數字減去除數 (`s0`),並將除數加上 `2r`
* 為 0 則不做任何行為
2. 各自位移 (一次處理 2 個 bit)
3. 沒有全部數字都處理的話,回到步驟 1.
```c=78
/* use floating add to find out rounding direction */
if (ix0 != 0) {
z = one - tiny; /* trigger inexact flag */
if (z >= one) {
z = one + tiny;
if (z > one)
q += 2;
else
q += (q & 1);
}
}
```
因在 63 行有額外 shift 一次 `ix0`,所以我們做完迴圈後實際上小數點後有 24 bit 的數字,最後一個 bit 可以用來做 round 來讓結果更正確。
將 1 與極小的數字做運算來判斷當前系統對 float point 運算的規則,並依照此規則來做 round。
```c=90
ix0 = (q >> 1) + QQ1;
ix0 += (m << QQ2);
INSERT_WORDS(z, ix0);
return z;
```
`q >> 1` 是因為我們多計算一個 bit 用來做 round,要把最後一個 bit 去掉,讓 mantissa 為 23 bit。
最後要把數字轉換為 IEEE 754 的格式,因要把 m 轉換為 excess-127 格式,並移到 float 格式中 exponent 的位置,所以 `QQ1` 與 `QQ2` 分別為 `0x3f000000` 與 `23`。
#### 延伸題目
* 解釋上述程式碼何以運作
* 搭配研讀 [以牛頓法求整數開二次方根的近似值](http://science.hsjh.chc.edu.tw/upload_works/106/44f6ce7960aee6ef868ae3896ced46eb.pdf) (第 19 頁)
* 試改寫為更有效率的實作,並與 FPU 版本進行效能和 precision / accuracy 的比較
* 練習 LeetCode [69. Sqrt(x)](https://leetcode.com/problems/sqrtx/),提交不需要 FPU 指令的實作
實作 [Wikipedia](https://en.wikipedia.org/wiki/Methods_of_computing_square_roots#Binary_numeral_system_(base_2)) 上開根號程式:
```c
int mySqrt(int x){
uint32_t t = 0;
uint64_t b = 0x100000000;
while (b > x)
b >>= 2;
while (b) {
if (x >= t + b) {
x = x - t - b;
t = (t >> 1) + b;
}
else {
t >>= 1;
}
b >>= 2;
}
return t;
}
```
Runtime: **4 ms**, faster than **67.45%** of C online submissions for Sqrt(x).
Memory Usage: **5.8 MB**, less than **46.78%** of C online submissions for Sqrt(x).
---
### 測驗 3
```c
int consecutiveNumbersSum(int N)
{
if (N < 1)
return 0;
int ret = 1;
int x = N;
for (int i = 2; i < x; i++) {
x += ZZZ;
if (x % i == 0)
ret++;
}
return ret;
}
```
#### `ZZZ`
- [x] `(d)` `1 - i`
數學式:
$$
N - \frac{k(k-1)}{2}=kx
$$
對應到程式中,`i` 為式子中的 `k`,`x` 為相減後的值,每次迴圈皆減掉下個數字 `k`,所以答案為迴圈內應為 `x -= (i - 1)`,故答案為 `1 - i`。
#### 延伸題目
* 嘗試改寫為更有效率的實作
參考 [討論區](https://leetcode.com/problems/consecutive-numbers-sum/discuss/214130/C%2B%2B-detailed-explanation-(5-lines)) 的程式,因為 $N$ 可以拆成連續數字 $(x + 1), (x + 2), ..., (x + k)$
可以寫成:
$$
N = kx + \frac{k(k + 1)}{2} \\
2N = k(2x + k + 1)
$$
等式右邊可看出一定為**一奇數 * 一偶數**,且式子中 $x$ 可為任意正整數,表示我們只要找到兩個數字能將 $2N$ 分解成一奇數一偶數,就能分解 $N$ 成連續正整數。
因偶數乘以奇數必為偶數,所以我們可以從數字 $N$ 的中任選一大於 2 的質因數,則剩餘的部分必為偶數 (因 $2N$ 為偶數),滿足上述分解的條件。
所以問題被簡化成:找到數字 $N$ 的所有大於 2 的質因數的可能組合
實作程式如下:
```c
int consecutiveNumbersSum(int N) {
N >>= __builtin_ctz(N);
int ans = 1, d = 3;
while (d * d <= N) {
int e = 0;
for (; N % d == 0; N /= d, ++e);
ans *= e + 1;
d += 2;
}
if (N > 1) ans <<= 1;
return ans;
}
```
質數用奇數來檢驗,因後處理的奇數會被前面的奇數處理,故不會有多蒜的情況,可以改為查質數表來加快效率。
一般情況質因數皆小於 $\sqrt{N}$,但當 $N$ 本身為質數時也須計算一種可能,故最後有個條件式判斷 $N$ 是否被完全分解。
程式時間複雜度與題目程式一樣為 $O(\sqrt{N})$,但在 leetcode 上此版本的運行時間為 `0ms`,較題目的 `4ms` 還要有效率。
###### tags: `linux2020`
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet