# Introduction to Dynamic Programming
## About me
* Carlos Gonzalez Oliver
* Emai: carlos@ozeki.io
* Homepage: carlosoliver.co
**My interests:**
* Structural Bioinformatics
* Graph algorithms
* Representation learning
_Some questions I ask:_
* _How can we efficiently search through graph databases?_
* _What kinds of patterns can we discover in datasets of graphs?_
* _Can we model biological systems using efficient data structures to learn about how they function?_
---
## Dynamic Programming (DP)
| | |
| -------- | -------- |
|  | <ul> <li>Richard Bellman, 1950s, working at RAND institute.</li> <li>Picked the name "Dynamic Programming" to please his boss. </li>|
* Method for solving a large problem by breaking it down into smaller sub-problems.
Applications
* **Bioinformatics: protein and RNA folding, sequence alignment**
* Speech recognition: Viterbi's algorithm
* Time series modeling: Dynamic time warping
* Search: string matching
* **Scheduling: weighted interval**
* Music: Beat tracking
* Routing: shortest path problems
---
## Objectives
After this lesson we should be able to:
::: info
- [ ] Recognize the **ingredients** needed to solve a problem with DP.
- [ ] Write down and execute some simple DP algorithms.
- [ ] Be able to implement a DP algorithm for a real-world problem (homework).
:::
---
## Basic Intuition
* What is:
* $1 + 1 + 1 + 1 + 1 + 1 = ?$
* Now what is:
* $1 + 1 + 1 + 1 + 1 + 1 + 1 = ?$
<pre>
</pre>
---
## First ingredient: Optimal Substructures
::: info
The optimal structure can be built by combining optimal solutions to smaller problems.
:::
E.g. Fibonacci numbers
* $Fib(0) = 0$
* $Fib(1) = 1$
* $Fib(n) = Fib(n-1) + Fib(n-2)$
Recursive algorithm:
```
```
---
## Second ingredient: Overlapping Substructures
:::info
The same subproblem's solution is used multiple times.
:::
```python=
def fib(n):
if n == 0:
return 0
if n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
```
Call tree `fib(6)`:
```
```
Recursive solution is $\mathcal{O}(2^n)$.
---
## Can we do better?
:hand:
`M-fib(n)`:
```
```
---
## An example _without_ overlapping subproblems.
**Binary Search**: Given a sorted array $A$ and a query element, find the index where the query occurs.
```python
def binary_search(A, left, right, query):
if low > high:
return None
mid = (left + right) // 2
if A[mid] == query:
return i
elif A[mid] > query:
return binary_search(A, left, mid-1, query)
else:
return binary_search(A, mid+1, right, query)
```
Call tree `binary_search(A=[ 15, 22, 32, 36, 41, 63, 75], left=0, right=4, query=75)`:
```
```
---
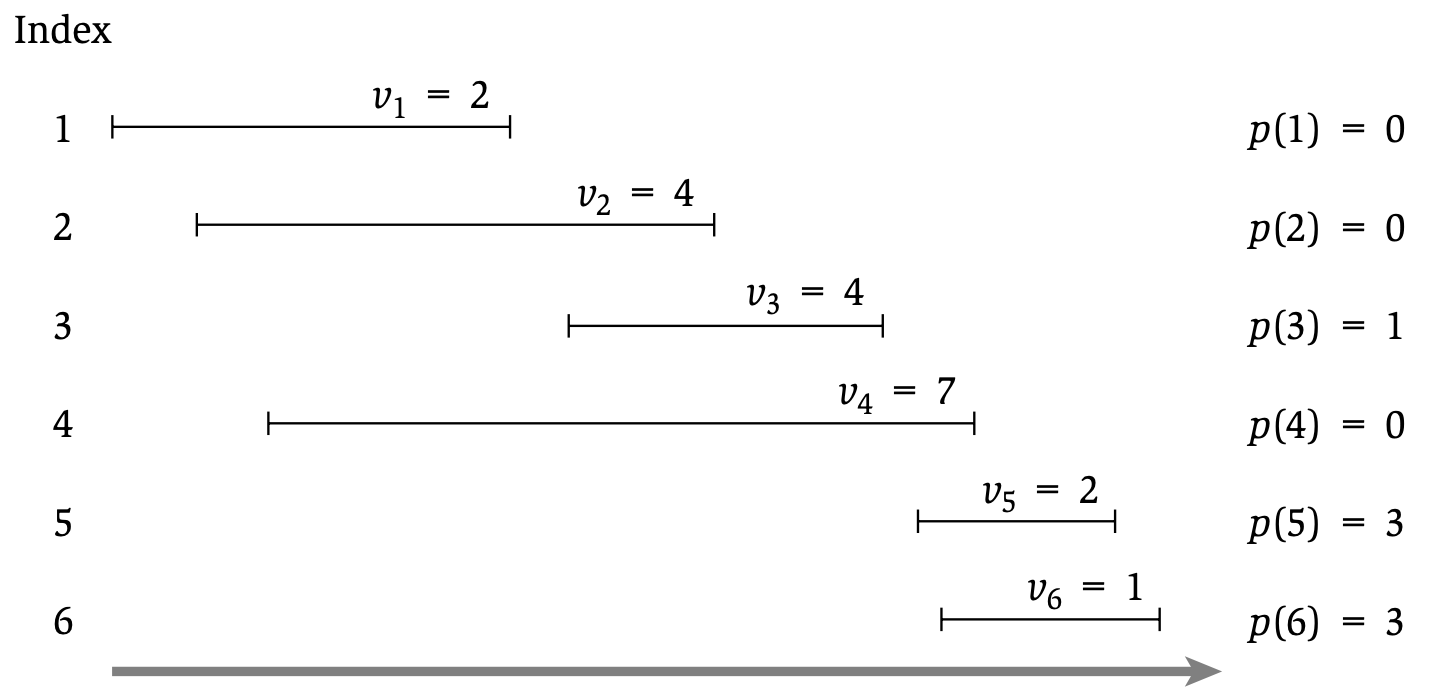
## Case study: Weighted Interval Scheduling
* **Input:** $n$ requests, labeled $\{1, .., n\}$. Each request has a start time $s_i$ and an end time $f_i$, and a __weight__ $v_i$.
* **Output:** a _compatible_ subset $S$ of $\{1, .., n\}$ that maximizes $\sum_{i \in S} v_i$.
:::info
$S$ is compatible iff all pairs of intervals in $S$ are non-overlapping.
:::
* Uses: resource allocation for computer systems, optimizing course selection.
Example:
```
```
---
## False start: greedy approach
* From "previous" lectures we know the greedy approach to the unweighted IS problem gives the optimal solution (i.e. pick item with earliest ending time)
Counterexample:
```
```
:::warning
The weights force us to consider all possible subproblems (i.e. local choice is not enough).
:::
---
## A helper function
Let us sort all intervals by increasing _finish_ time and let $p(j)$ return the latest interval $i$ that is still compatible with $j$.
---
## First ingredient: Optimal Substructure?
* Consider $\mathcal{O}_j$ to be the _optimal_ set of requests over all items $j$.
* Also consider the _weight_ of the best solution up to $j$ as $\mathrm{OPT}(j)$.
* There are two cases for the last request, $j$.:
Case 1
```
```
Case 2
```
```
---
## Optimal Substructure
Let $\textrm{OPT}(j)$ be the total weight of the optimal over intevals up to $j$.
We can now write an expression for computing $\textrm{OPT}(j)$:
```
```
**Ingredients**
- [x] Optimal Substructure
- [ ] Overlapping Subproblems
---
## First algorithm
Now we can write down a recursive algorithm that gives us the maximum weight over $1, ..., n$.
`compute_OPT(j)`:
```
```
---
## Ingredient 2: Overlapping Substructures
Let's build the execution tree for our recursive algorithm on this example:
`compute_OPT(6)`:
```
```
Runtime:
```
```
**Ingredients**
- [x] Optimal Substructure
- [x] Overlapping Subproblems
---
## Memoization
* Key idea in DP: remember solutions to sub-problems you already computed.
New algo: `M_compute_OPT(j)`
```
```
Runtime:
```
```
---
## Are we done?
* Recall $\textrm{OPT}(j)$ is just a number, we want the _set_ of intervals with the score $\textrm{OPT}(j)$... i.e. $\mathcal{O}_j$.
* **Traceback** is a key idea in DP. We reconstruct the solution backwards from the $M$ array using the recurrence.
* **Obervation:** We know that an interval $j$ belongs to $\mathcal{O}_j$ if:
```
```
Now our DP execution has two steps:
1) Fill $M$
2) Reconstruct solution from $M[n]$
---
## Full Example
Fill $M$ and get $\mathcal{O}_n$:
```
```
---
## Recap
* Dynamic Programming works well when we have a problem structure such that:
* Combining sub-problems solves the whole problem
* Sub-problems overlap
* We can often reduce runtime complexity from exponential to polynomial or linear.
* Steps to solving a problem with DP:
* Define subproblems:
* $\textrm{fib}(n-1)$ and $\textrm{fib}(n-2)$ are subproblems of $\textrm{fib(n)}$
* Write down the recurrence that relates subproblems.
* $\textrm{fib}(n) = \textrm{fib}(n-1) + \textrm{fib}(n-2)$
* Recognize and solve the base cases.
* $\textrm{fib}(0) = 1$, $\textrm{fib}(1) = 1$
* Implement a solving methodology. (e.g. memoization, tabulation is also an option)
---
## General interest: RNA folding
* RNA molecules are essential to all living organisms.
* Knowing the sequence is easy but not so informative, knowing the structure is hard but tells us a lot about the molecule's function.
---
## A Sketch of Nussinov's Algorithm
* First attempt at solving this problem
| | |
| -------- | -------- |
| <img src="https://upload.wikimedia.org/wikipedia/commons/thumb/5/5a/Ruth_Nussinov.png/440px-Ruth_Nussinov.png" width="200px"> | Ruth Nussinov, designed the first RNA folding algo in 1977. |
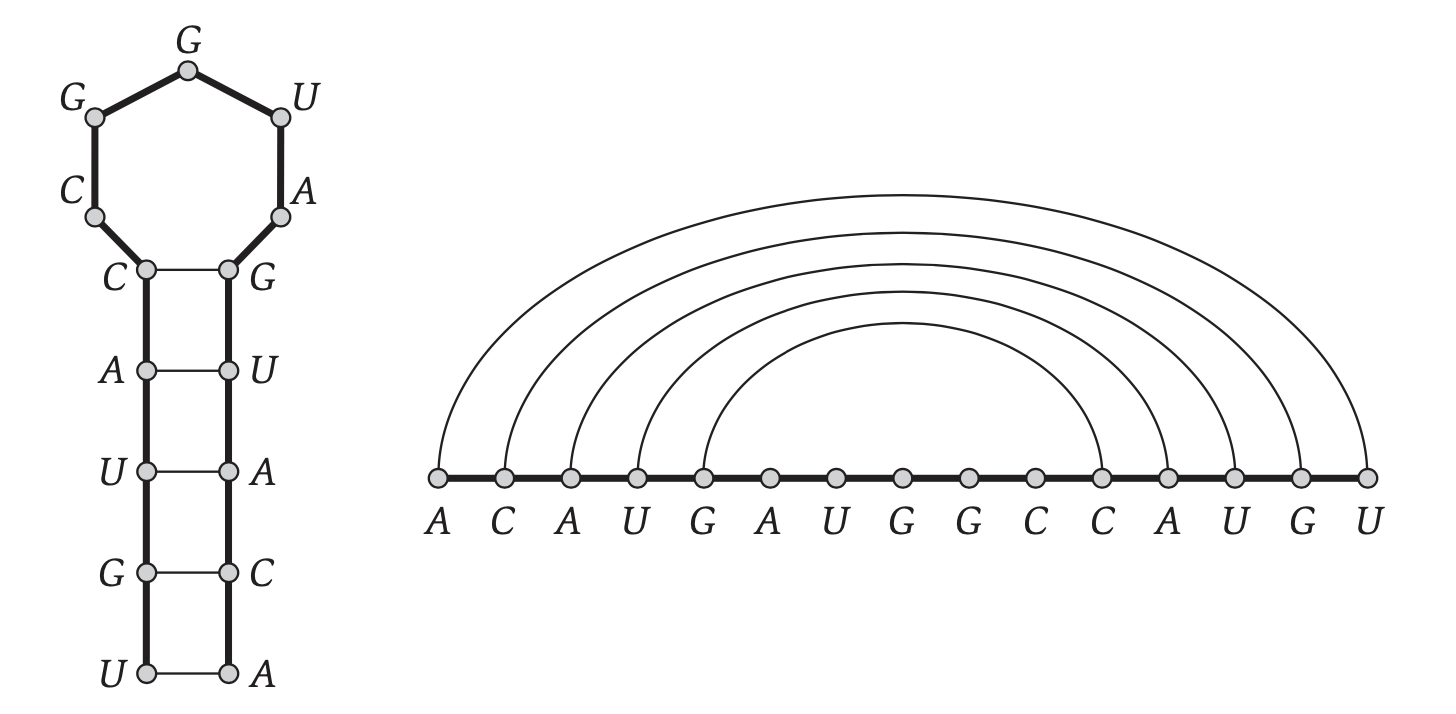
* In CS terms, an RNA is a string on a 4-letter alphabet.
* An RNA __structure__ is a pair of indices over the string with certain constraints.
---
## RNA folding rules
We use some fairly realistic constraints on admissible structures:
:::info
1. Only `A-U`, `U-A` and `C-G`, `G-U` form pairs
2. Pairs shall not cross (nestedness).
3. Start and end of a pair should be separated by at least $\theta$ spaces (remove steric clashes).
4. The best structure is the one that forms the most pairs (stability). e.g each pair adds 1 to the score.
:::
This lets us identify the problem structure needed for a DP solution:
Consider an optimal set of pairs $\mathcal{O}_{ij}$ between two indices $(i, j)$, and the score of the olution $\mathrm{OPT}(i, j)$. We have two cases for index $j$:
Case 1. $j$ is not in $\mathcal{O}_{ij}$:
```
```
**Note we introduce a new variable** $\rightarrow$ 2 dimensional DP.
Case 2. $j$ is in $\mathcal{O}_{ij}$:
```
```
**Ingredients?**
- [ ] Optimal substructures
- [ ] Overlapping subproblems
From this we can build our recurrence that fills the table up to $\mathrm{OPT}(1, L)$.
```
```
**Bonus Questions:** What is the runtime for filling the table?
:::success
If you want an exercise sheet to learn how to implement this send me an email `carlos@ozeki.io`.
:::
---
Sign in with Wallet
Connect another wallet