---
title: 'Binary Tree'
disqus: hackmd
---
[TOC]

Binary Tree
===
* 又稱為 Knuth Tree , Ordered Tree
* 有限集合，**可以為空**
* 若非空則由 左子樹、右子樹 構成
* 每個 Node 之 Degree：0~2
* 子樹 有**次序**之分
#### 次序
1. 子樹 B,C 在 Tree 中視為相同
2. 在 Binary Tree 中視為不同

---

## Difference with Tree
| | Tree | Binary Tree |
|:------:|:-----------:|:------:|
| 可否為空 | $No$ , 至少一樹根 | $Yes$ |
| $Node Degree$ (存在 $Root$ 時) | $\geq 0$ | $0,1,2$ |

---

## Three Theories of Binary Tree
### [定理一] 第 i Level 最多 $Node$ 數
> [color=#52d356]**Def : 高度起始點為 1**
**Formula**：$2^{i-1}\ ，i\geq1$
:::warning
#### 證明方式：數學歸納法
:::

> [color=#52d356]**Def : 高度起始點為 0**
**Formula**：$2^i\ ，i\geq0$
:::success
#### 證明方式：數學歸納法

:::

---

### [定理二] Height 為 k 的最多 Node 數 (整棵樹)
> [color=#52d356]**Def : 高度起始點為 $1$**
> **Formula**：$2^k-1\ , \ k\geq1$
:::warning
#### 根據定理一：2^0^ + 2^1^ + ... + 2^k-1^ 從 Level 1 依序累加至 Level k
#### 根據等比級數 = $\frac{2^k-2^0}{2-1}$
#### = $2^k-1$
:::

> [color=#52d356]**Def : 高度起始點為 $0$**
> **Formula**：$2^{(k+1)}-1\ , \ k\geq0$
:::success
#### 根據定理一：$2^0 + 2^1 +\ ...\ + 2^k$ 從 $Level\ 0$ 依序累加至 $Level\ \ k$
#### 根據等比級數 $=\frac{2^{(k+1)}-2^0}{2-1}$
#### = $2^{(k+1)}-1$
:::
**藉由上述定理我們可以對 Node 數取 log 反推回高度**

---

### [定理三] Branch(Degree) 與 Node 關係
* Leaf 數 = L (綠色node)
* Branch 數 = B (藍、紅 Degree)
* Nodes 數 = N
* Degree 為 1 的 Nodes = d~1~ (藍色node)
* Degree 為 2 的 Nodes = d~2~ (紅色node)

digraph graphname{
    1 [label="Root" color=red];
    2 [label="A" color=red];
    3 [label="B" color=blue];
    4 [label="C" color=blue];
    5 [label="leaf" color = green ];
    6 [label="leaf" color = green ];
    7 [label="Null" style=dashed]
    8 [label="leaf" color = green ];
    9 [label="Null" style=dashed]
    10 [label="Null" style=dashed]
    11 [label="Null" style=dashed]
    12 [label="Null" style=dashed]
    13 [label="Null" style=dashed]
    15 [label="Null" style=dashed]
    16 [label="Null" style=dashed]
    
    1 -> 2 [color=red]
    1 -> 3 [color=red]
    2 -> 4 [color=red]
    2 -> 5 [color=red]
    3 -> 6 [color=blue]
    3 -> 7 [style=dashed]
    4 -> 8 [color=blue]
    4 -> 9 [style=dashed]
    5 -> 10[style=dashed]
    5 -> 11[style=dashed]
    6 -> 12[style=dashed]
    6 -> 13[style=dashed]
    8 -> 15[style=dashed]
    8 -> 16[style=dashed]
}

:::info
在上述圖例得知

1. <font color=red>$L + d_1~ + d_2 = Node$ 總數 </font>
2. 二元樹中 Degree 為 0~2 ( 之後的 m-way Tree 同理 )
Degree 為 1 的 Node 有 1 個 Branch
Degree 為 2 的 Node 有 2 個 Branch
而 <font color=red>$(Branch$ $數)$ $+ 1 = Node$ 總數 </font>
所以 $(1 * d_1 + 2 * d_2) +1 = Node$ 總數

3. 藉由上述兩公式我們可以整理出
$L + d_1 + d_2 = Node總數 = d_1 + 2d_2 + 1$
<font color=red>$L = d_2 + 1$ </font> $(\ 樹葉 = Degree\ 為\ 2\ 的\ Nodes + 1\ )$
:::

---

整理一下目前有的公式
:::warning
* **Def : 高度起始點為 1**

1. 第 i Level 最多 Node 數：**$2^{k-1}$** -----------**( 2的高度-1次方 )**
2. Height 為 k 的最多 Node 數：**$2^k-1$** ----**( 2的高度次方-1 )**
3. Node總數 = **$L + d_1 + d_2$** --------------**( 樹葉 + Deg1的Nodes + Deg2的Nodes )**
4. Node總數 = **( $1 * d_1 + 2 * d_2 ) + 1$** ----**( 1倍Deg1的Nodes + 2倍Deg2的Nodes +1 )**
5. Node總數 = **$Branch + 1$** ----------------**( 分支+1 )**
7. 樹葉 = **$d_2 + 1$** -----------------------------**( Deg2的Nodes+1 )**
8. Branch = 所有 Degree 合
:::

> [color=#deed3d]補充：針對 3. 4. 的設計題
某樹之 $Degree\ of\ tree = k$ ( 最大Degree 為k )
$Degree\ 為\ i$ 的 $Nodes$ 有 $i$ 個 ，$1\leq i \leq k$， 求 $Leaf$ 總數？

> [color=#deed3d]
> **Sol**：
> 1. 根據 `3.` $Nodes = Deg-0$ 個數 $(Leaf) + Deg-1$ 個數 $+ ... + Deg-i$ 個數
>
> 1. 從題目 <font color = red>$1\leq i \leq k$</font> 得 **$Nodes = Leaf + 1 + 2 + ... + k$**
根據等差級數 **$Nodes = Leaf\ +$** 
> 2. 根據 `4.` **Nodes = ( 1 * d~1~ + 2 * d~2~ ) + 1**
從題目 <font color = red>$Degree\ 為\ i\ 的\ Nodes\ 有\ i\ 個$</font> 得 **( 1 * 1 + 2 * 2 + ... + k * k ) + 1**
根據平方合 **Nodes =** 
> 3. 移項即可得 **Leaf =** 

>[color=#deed3d] 關鍵字 Degree-0 (Leaf) , Degree-1 , Degree-2 , Height , Nodes , Branch 互通到熟練吧

---

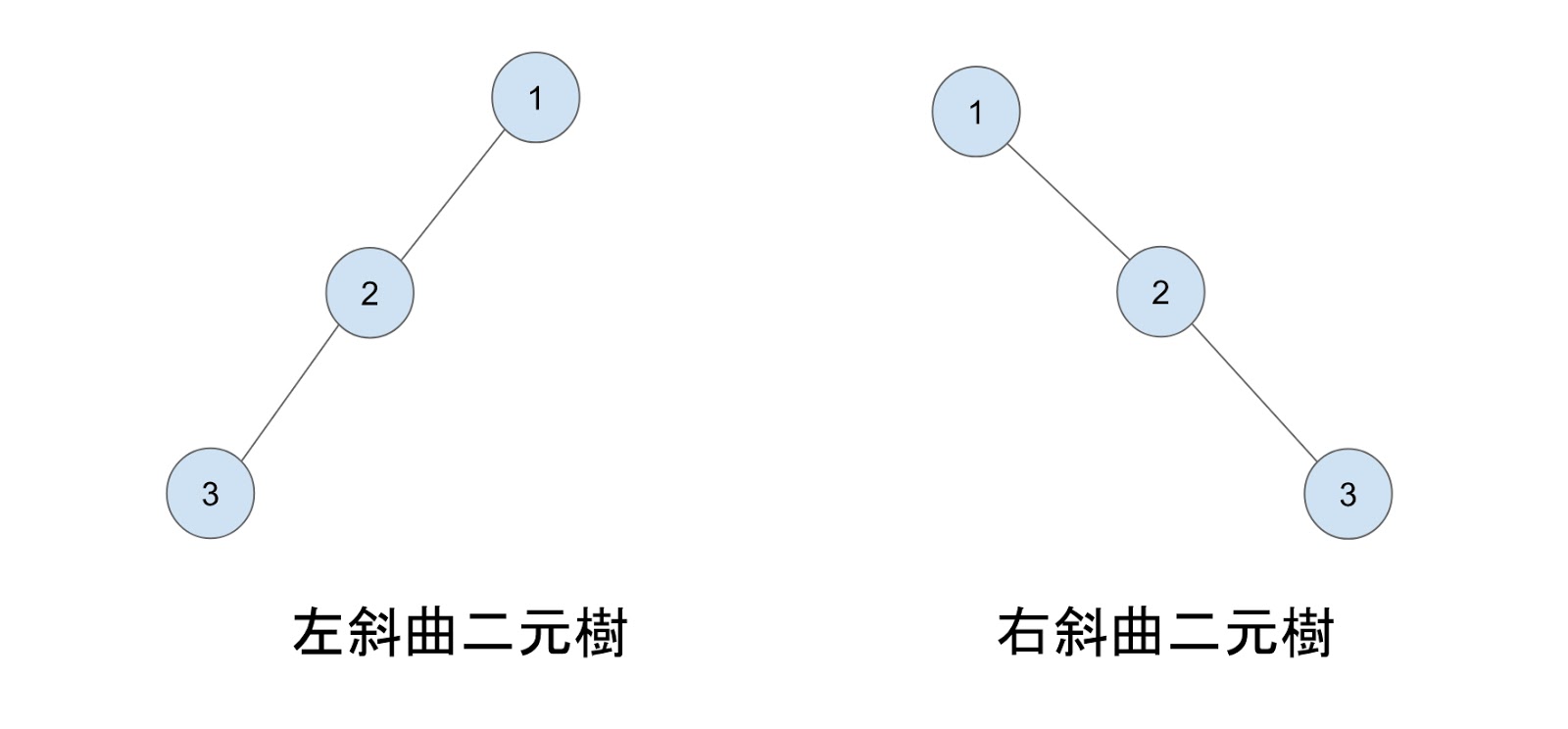
## Type of Binary Tree
### Skewed Tree - 斜曲樹
* 左斜曲：每個非樹葉節點只有左子點。
* 右斜曲：每個非樹葉節點只有右子點。


---

### Complete Binary Tree
* 由上至下由左而右依序填入
:::danger
* **Def：編號 (Index) 起始點 1 , 某Node編號 = n**
Left Child 編號 = **Parent 編號 * 2**
Right Child 編號 = **Parent 編號 * 2 + 1**
n's Parent 編號 = $\left \lceil \frac{(n-1)}{2} \right \rceil$
:::

:::success
* **Def：編號 (Index) 起始點 0 , 某Node編號 = n**
Left Child 編號 = **Parent 編號 * 2 + 1**
Right Child 編號 = **Parent 編號 * 2 + 2**
n's Parent 編號 = $\left \lfloor \frac{(n-1)}{2} \right \rfloor$
:::

> [color=#] 計算完請判斷該樹是否存在此節點
Parent , Child 編號關係證明：數學歸納法（略）

:::info
**Def：高度起始點 1**
* 根據定理二得出 k Level 的最大 Node 總數 = $2^k-1$
* 根據 Complete Binary Tree 特性，若高度 $k$ ，則 $Nodes$ 必介於
$k$ 層第 $1$ 個：$(2^{k-1}-1)+1$ (藍色 Nodes) 到
$k$ 層最後一個 ： $2^k-1$ $Nodes$ 之間
:::

digraph graphname{
    1 [label="Root" color=blue];
    2 [label="A" color=blue];
    3 [label="B" color=blue];
    4 [label="D" color=blue];
    5 [label="E" color=red style=dashed];
    6 [label="F" color=red style=dashed];
    7 [label="G" color=red style=dashed];
    
    
    
    1 -> 2
    1 -> 3 [label="     若 Level=3 則必含有藍Node"]
    2 -> 4
    2 -> 5
    3 -> 6 
    3 -> 7 [label="   紅 Node為
   Level=3 Node總數合理範圍"]
}

:::info
* 因此我們得知，給定一 Complete Binary Tree

$2^{k-1} \leq Nodes \leq 2^k-1$

:::

---

### Strictly binary tree
* 除了 Leaf 以外，每個 Node 都有兩個 Child。
* $Nodes = n_0+n_2$
>

---

### Full Binary Tree
* 長滿整棵樹，Nodes 等同定理二


---

## Binary Tree Representation in C

### Array
> [color=#7ef466] **Def：編號 (Index) 起始點 1 , 高度 = k**
> 1. 假設 k = 3
> 2. 建立一個 `int tree[]` 陣列，空間為：2^k^-1 = 8 = s
> Index：0 ,1 ,2 ,3 ,4 ,5 ,6 ,7
> 3. 若使用迴圈，終止條件為
> * i<2^k^-1 = 8-1 = s-1
> * i<=2^k^-2 = 8-2 = s-2
> 4. 存在情況下，設某點為 n
> * Root = `tree[1]`
> * n's Parent = `tree[n/2]` * 請注意程式語言對浮點數處理特性
> * n's Left Child = `tree[2*n]`
> * n's Right Child = `tree[2*n+1]`

digraph graphname{
    0 [label="tree[0]" color=red]
    1 [label="tree[1]"]
    2 [label="tree[2]"]
    3 [label="tree[3]"]
    4 [label="tree[4]"]
    5 [label="tree[5]"]
    6 [label="tree[6]"]
    7 [label="tree[7]"]
    
    1->2
    1->3
    2->4
    2->5
    3->6
    3->7
}

---

> [color=#7ef466] **Def：編號 (Index) 起始點 0 , 高度 = k**
> 1. 假設 k = 3
> 2. 建立一個 `int tree[]` 陣列，空間為：2^k+1^-1 = 8 = s
> Index：0 ,1 ,2 ,3 ,4 ,5 ,6 ,7
> 3. 若使用迴圈，終止條件為
> * i<2^k+1^-1 = 8-1 = s-1
> * i<=2^k+1^-2 = 8-2 = s-2
> 4. 存在情況下，設某點為 n
> * Root = `tree[0]`
> * n's Parent = `tree[(n-1)/2]` * 請注意程式語言對浮點數處理特性
> * n's Left Child = `tree[2*n+1]`
> * n's Right Child = `tree[2*n+2]`

digraph graphname{
    0 [label="tree[0]"]
    1 [label="tree[1]"]
    2 [label="tree[2]"]
    3 [label="tree[3]"]
    4 [label="tree[4]"]
    5 [label="tree[5]"]
    6 [label="tree[6]"]
    7 [label="tree[7]"  color=red]
    
    0->1
    0->2
    1->3
    1->4
    2->5
    2->6
}

:::success
**優點：**
1. 容易存取左右 Child
2. 若 Perfect Binary Tree 則完美利用空間 **(Def：root start from index 0)**
:::

:::danger
**缺點：**
1. 插入、刪除 不便
2. Height 改變則需重新宣告新陣列
3. 對於 Skewed Binary Tree 極為浪費
**( Def：root start from index 0 , Height = k = Nodes , 2^k^-1-k 未使用)**
:::

---

### Linked List
> [color=#7ef466] **Def：Nodes = n**
> 1. Linked List 中的 Link 相當於定理所提到的 Branch
> 而在程式當中每個 Node 結構都有兩條 Link，有別於定理中的觀念
> 我們會將指向 Null 的 Link 也一併算進去 (藍Link)
> 實際上公式還是可行的，只要我們將 Null 也視為 Node
>
> 2. 不過我們想探討的是沒有使用到的 Link (藍Link)
> 以下將 Branch 視為 Link
>
> 3. Links = 所有 Degree 合
> 因為每一個 Node 皆有 2 個 Links
> => **所有的 Links = 2*n**
> 4. 根據定理
> **有使用到的 Links = n - 1**
>
> 5. 根據 `3.` ` 4.`得出
> =>所有的 Links - 有使用到的 Links = 未使用的 Links
> => **(2 * n) - (n-1) = n+1**
>
> 6. 可以這樣記 `n-1 (未使用的LINK) -> n (Nodes) -> n+1 (使用的LINK)`

digraph graphname{
    1 [label="Root"];
    2 [label="A"];
    3 [label="B"];
    4 [label="leaf"];
    5 [label="leaf"]
    6 [label="leaf"]
    7 [label="leaf"]
    8 [label="Null" style=dashed];
    9 [label="Null" style=dashed]
    10 [label="Null" style=dashed]
    11 [label="Null" style=dashed]
    12 [label="Null" style=dashed]
    13 [label="Null" style=dashed]
    14 [label="Null" style=dashed]
    15 [label="Null" style=dashed]
    
    
    1 -> 2 
    1 -> 3 
    2 -> 4 
    2 -> 5 
    3 -> 6 
    3 -> 7 
    4 -> 8 [color=blue]
    4 -> 9 [color=blue]
    5 -> 10[color=blue]
    5 -> 11[color=blue]
    6 -> 12[color=blue]
    6 -> 13[color=blue]
    7 -> 14[color=blue]
    7 -> 15[color=blue]
}

:::success
**優點：**
1. Node 插入、刪除方便
2. 對於 Skewed Binary Tree 完美利用空間
:::

:::danger
**缺點：**
1. 各 Node Parent 不好尋找
2. 幾乎有 $50\%\ Links$ 未使用到，即指向 $NULL$ 的 $Link$
**(因此延伸出了 [Threaded Binary Tree - 引線二元樹](https://hackmd.io/xmKt-0W7SMap59uIYg8-jw#Thread-Binary-Tree---%E5%BC%95%E7%B7%9A%E4%BA%8C%E5%85%83%E6%A8%B9))**
:::

---

## Binary Tree Traversal

* to be continued

---

## Multiple Structures of One Binary Tree

* 回憶一下，以下兩種結構的樹，如果是 Tree 那麼兩顆是一樣的，如果是 Binary Tree 則是不同的

* 此節探討的就是當 Binary Tree 具有 N Nodes (N $\geq$ 1)，那麼這棵樹有幾種表示的方法，也就是他有幾種不同的結構


---

### Formula
* $\dfrac{1}{n+1}$ $\left(\begin{array}{ccc}2n \\n\\\end{array}\right)$

* 給 3 Nodes 畫出所有的可能的 Binary Tree


* Solution：$\dfrac{1}{3+1}$ $\left(\begin{array}{ccc}2*3 \\3\\\end{array}\right)=5$

## Proof
to be continued
p.194

---

###### tags: `Data Structure`