owned this note
owned this note
Published
Linked with GitHub
---
tags: vaje, or, grafi
hackmd: https://hackmd.io/ylfGqxHgSxGzFfAoe5FqQg
plugins: mathjax
---
# Operacijske raziskave - vaje 10.5.2021
---
## Iskanje v globino
```python
class Graf:
...
def DFS(G, koreni=None, previsit=None, postvisit=None):
def nothing(u, v):
pass
if koreni is None:
koreni = G.vozlisca()
if previsit is None:
previsit = nothing
if postvisit is None:
postvisit = nothing
globina = {}
stars = {}
def obisci(u, v=None):
if u in globina:
return
globina[u] = 0 if v is None else globina[v] + 1
stars[u] = v
previsit(u, v)
for w in G.sosedi(u):
obisci(w, u)
postvisit(u, v)
for w in koreni:
obisci(w)
for u in G.vozlisca():
if u not in globina:
globina[u] = float('inf')
stars[u] = None
return (globina, stars)
```
Časovna zahtevnost: $O(m) + O(n)$ klicev funkcij `previsit` in `postvisit`
---
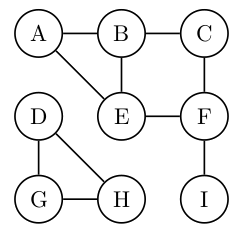
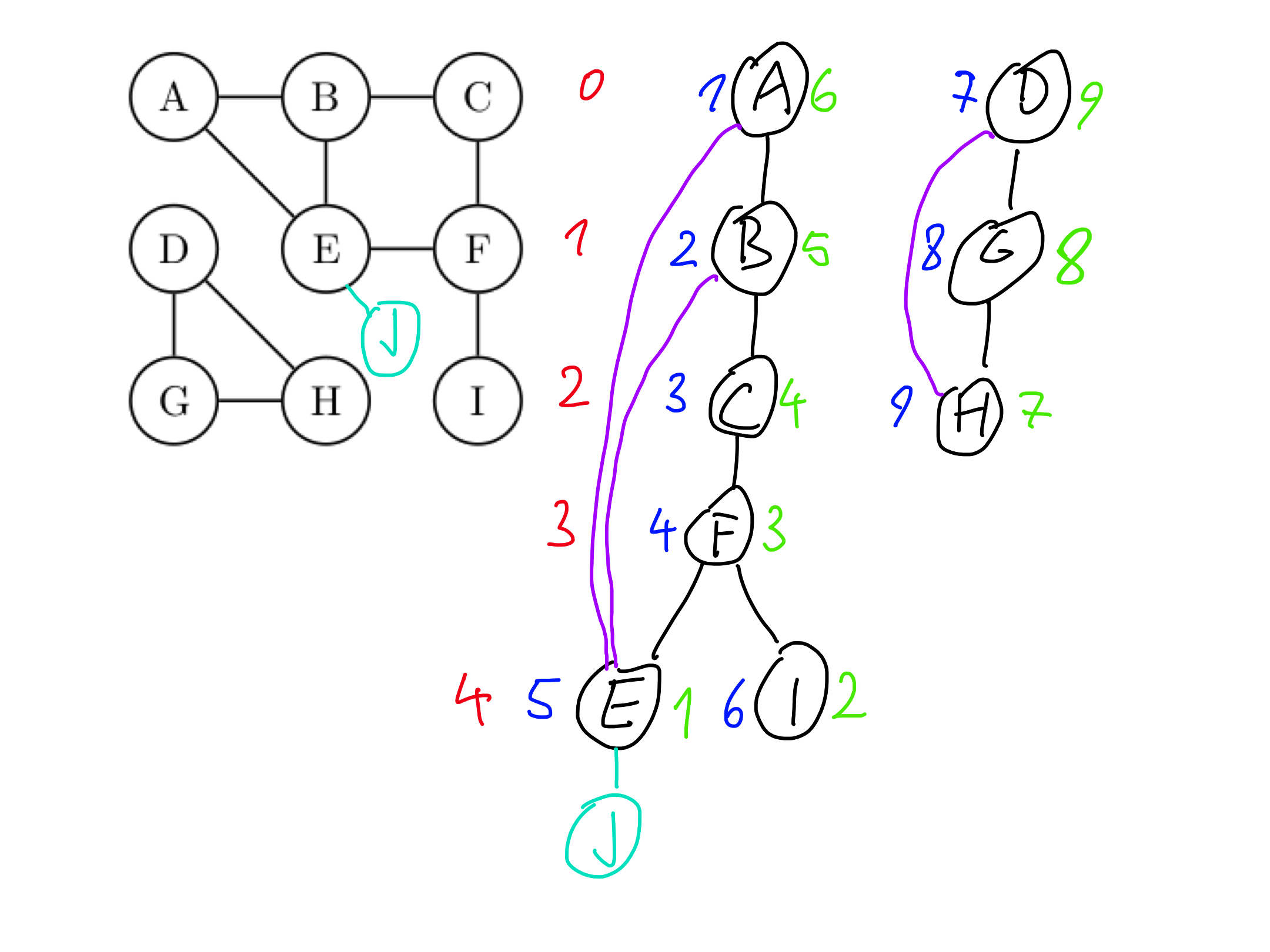
### Naloga 1
Na sledečem grafu izvedi iskanje v globino. V primerih, ko imaš več enakovrednih izbir, upoštevaj abecedni vrstni red. Za vsako povezavo določi, ali se nahaja v drevesu iskanja v globino.
----
---
## Bellman-Fordov algoritem
```python
class UtezenDigraf(Digraf):
...
def bellmanFord(G, koren):
razdalja = {v: 0 if v == koren else float('inf')
for v in G.vozlisca()}
stars = {koren: None}
naslednji = {koren}
for i in range(len(G)):
if len(naslednji) == 0:
break
trenutni, naslednji = naslednji, set()
for v in trenutni:
d = razdalja[v]
for w, r in G.utezeniSosedi(v).items():
r += d
if r < razdalja[w]:
razdalja[w] = r
stars[w] = v
naslednji.add(w)
else: # če se for zanka ne konča z break
if len(naslednji) > 0:
raise ValueError("graf ima negativen cikel")
return (razdalja, stars)
```
Časovna zahtevnost: $O(mn)$
---
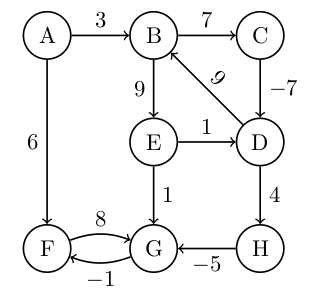
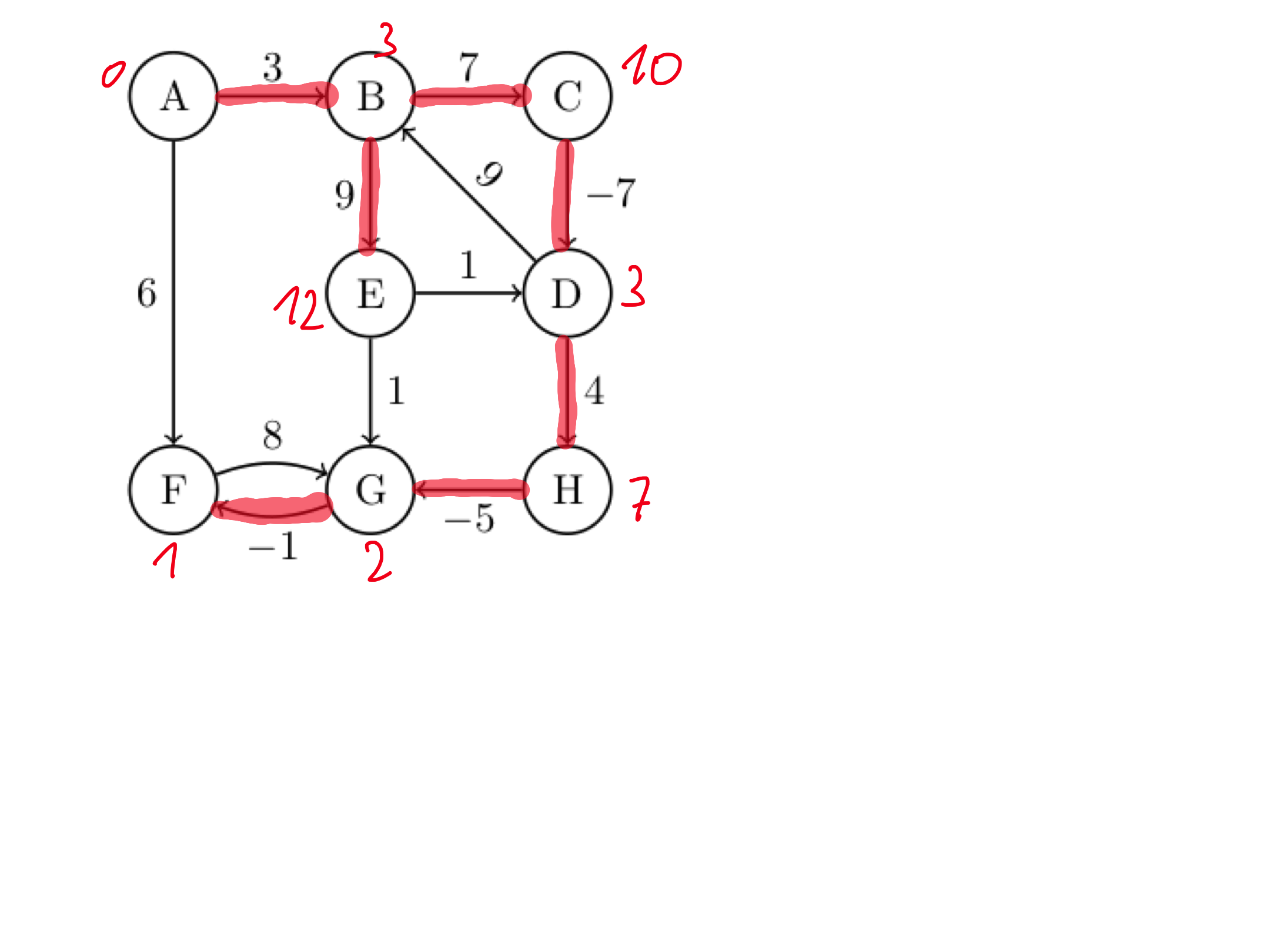
### Naloga 2
S pomočjo Bellman-Fordovega algoritma določi razdalje od vozlišča $A$ do ostalih vozlišč.
----
| vozlišče | A | B | C | D | E | F | G | H |
| --------- | --- | --- | ---- | --- | ---- | --- | ---- | --- |
| korak 0 | 0 | | | | | | | |
| korak 1 | | 3/A | | | | 6/A | | |
| korak 2 | | | 10/B | | 12/B | | 14/F | |
| korak 3 | | | | 3/C | | | 13/E | |
| korak 4 | | | | | | | | 7/D |
| korak 5 | | | | | | | 2/H | |
| korak 6 | | | | | | 1/G | | |
| korak 7 | | | | | | | | |
| razdalja | 0 | 3/A | 10/B | 3/C | 12/B | 1/G | 2/H | 7/D |
---
## Topološko urejanje
Topološko urejanje vozlišč digrafa ${u_1}, {u_2}, \dots, {u_n}$: za vsako povezavo ${u_i} {u_j}$ velja $i < j$.
```python
class Digraf(Graf):
...
def topoloskoUrejanje(G):
stopnje = {u: len(G.vhodniSosedi(u)) for u in G.vozlisca()}
vrsta = {u for u, s in stopnje.items() if s == 0}
urejanje = []
while len(vrsta) != 0:
u = vrsta.pop()
urejanje.append(u)
for v in G.izhodniSosedi(u):
stopnje[v] -= 1
if stopnje[v] == 0:
vrsta.append(v)
if len(urejanje) < len(G):
raise ValueError("graf ima usmerjen cikel")
return urejanje
```
Časovna zahtevnost: $O(m)$
---
### Naloga 3
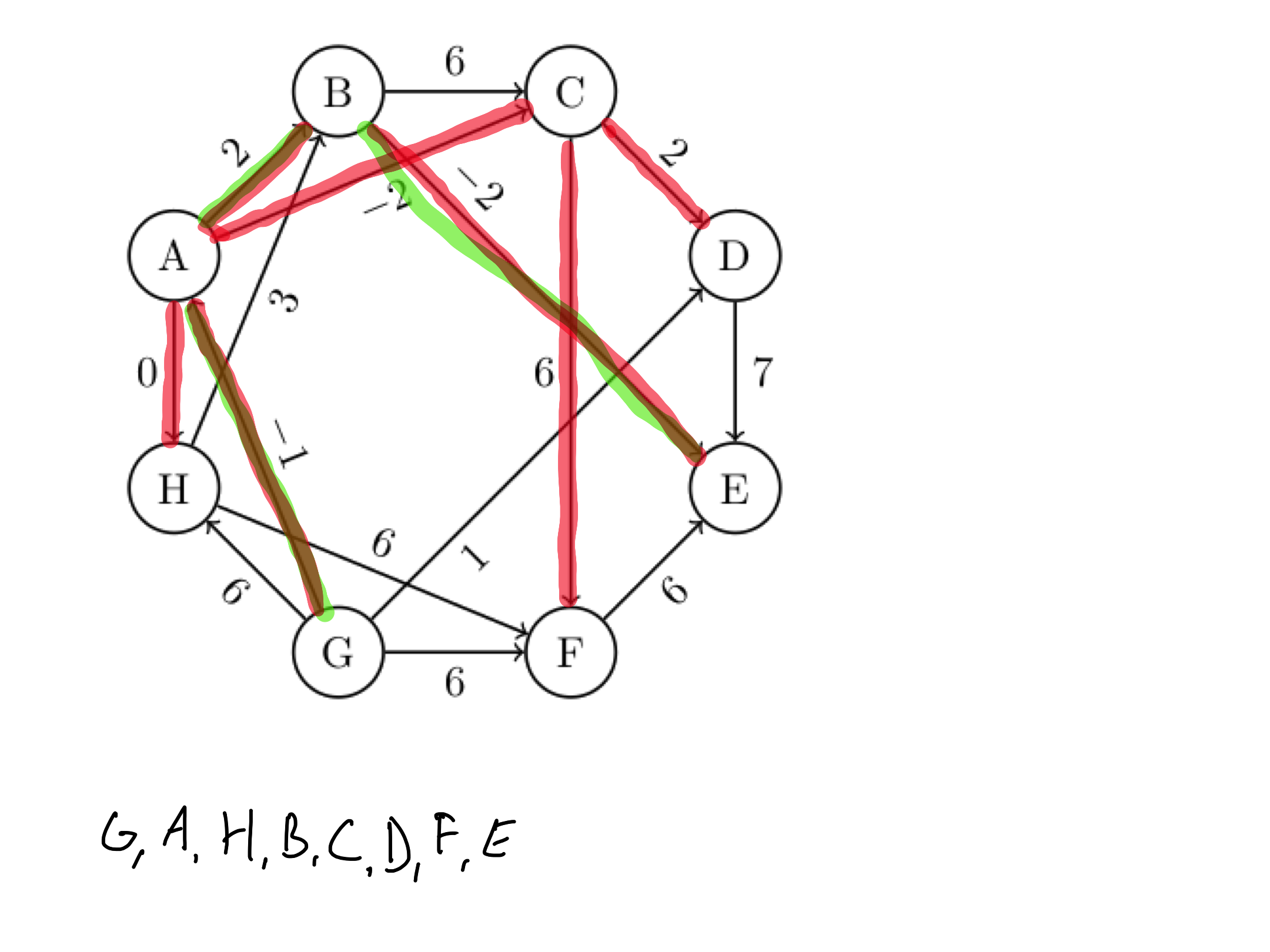
Dan je sledeči usmerjen acikličen graf.
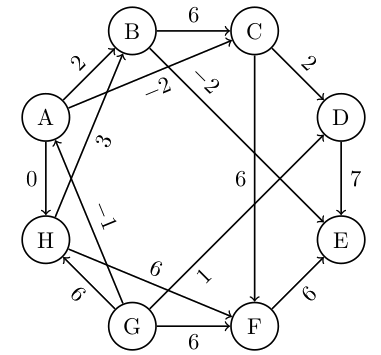
1. Poišči topološko ureditev vozlišč zgornjega grafa.
2. Poišči najkrajšo pot od vozlišča $G$ do vozlišča $E$.
3. Poišči najdaljšo pot od vozlišča $G$ do vozlišča $E$.
----
1. Topološka ureditev: $G, A, H, B, C, D, F, E$
2. | vozlišče | G | A | H | B | C | D | F | E |
| -------- | - | -- | -- | - | -- | -- | - | -- |
| razdalja | 0 | -1 | -1 | 1 | -3 | -1 | 3 | -1 |
| starš | | G | A | A | A | C | C | B |
Časovna zahtevnost: $O(m)$
---
### Naloga 4
Oviratlon je tekalna preizkušnja na 8 do 10 kilometrov dolgi poti z različnimi ovirami. Zanima nas, na koliko različnih načinov lahko pridemo od štarta do cilja. Dan je utežen usmerjen acikličen graf $G$ ter vozlišči $s$ in $t$, ki predstavljata štart oziroma cilj. Uteži na povezavah nam predstavljajo, na koliko načinov jih lahko prečkamo.
1. Reši nalogo za sledeči graf.
2. Zapiši algoritem, ki reši dani problem. Kakšna je njegova časovna zahtevnost?
Sign in with Wallet
