---
tags: vaje, rg, konveksnost
hackmd: https://hackmd.io/y7eMMlCHQduHQ01SCDlGbQ
plugins: mathjax
---
# Računska geometrija - vaje 28.11.2024

---

## Konveksnost

### Naloga 1

Naj bo $P$ množica točk v ravnini. Za vsako točko $p\in P$ definiramo

$$
\operatorname{cell}(p)=\{ x\in \mathbb{R}^2 \mid d(x,p)\leq d(x,p') \text{ za vsak }p'\in P\},
$$

kjer je $d(\cdot,\cdot)$ evklidska razdalja.
Pokaži, da je $\operatorname{cell}(p)$ konveksna množica za vsako točko $p\in P$.

----


$$
\operatorname{cell}(p) = \bigcap_{p' \in P \setminus \{p\}} \{x \in \mathbb{R}^2 \mid d(x,p)\leq d(x,p')\}
$$

$\operatorname{cell}(p)$ je presek polravnin, torej konveksnih množic, in je zato tudi sama konveksna množica.

---

### Naloga 2

Konveksen večkotnik $M$ je podan kot seznam oglišč, naštetih v smeri urinega kazalca. Opiši algoritem, ki v linearnem času uredi oglišča večkotnika $M$ po $x$-koordinatah. Ali se da tvoj algoritem ustrezno dopolniti, da bo (še vedno v linearnem času) deloval za poljuben večkotnik $M$?

----

* poiščemo skrajno levo oglišče
* združimo zgornji in spodnji rob
* časovna zahtevnost: $O(n)$

Za splošne večkotnike dokažimo, da če lahko urejamo oglišča v linearnem času, potem lahko urejamo poljubne sezname v linearnem času:

* Vhod: $x_1, x_2, \dots, x_n$
* Postavimo $x_0 = x_{n+1} = \min_{i=1}^n(x_i) - 1$
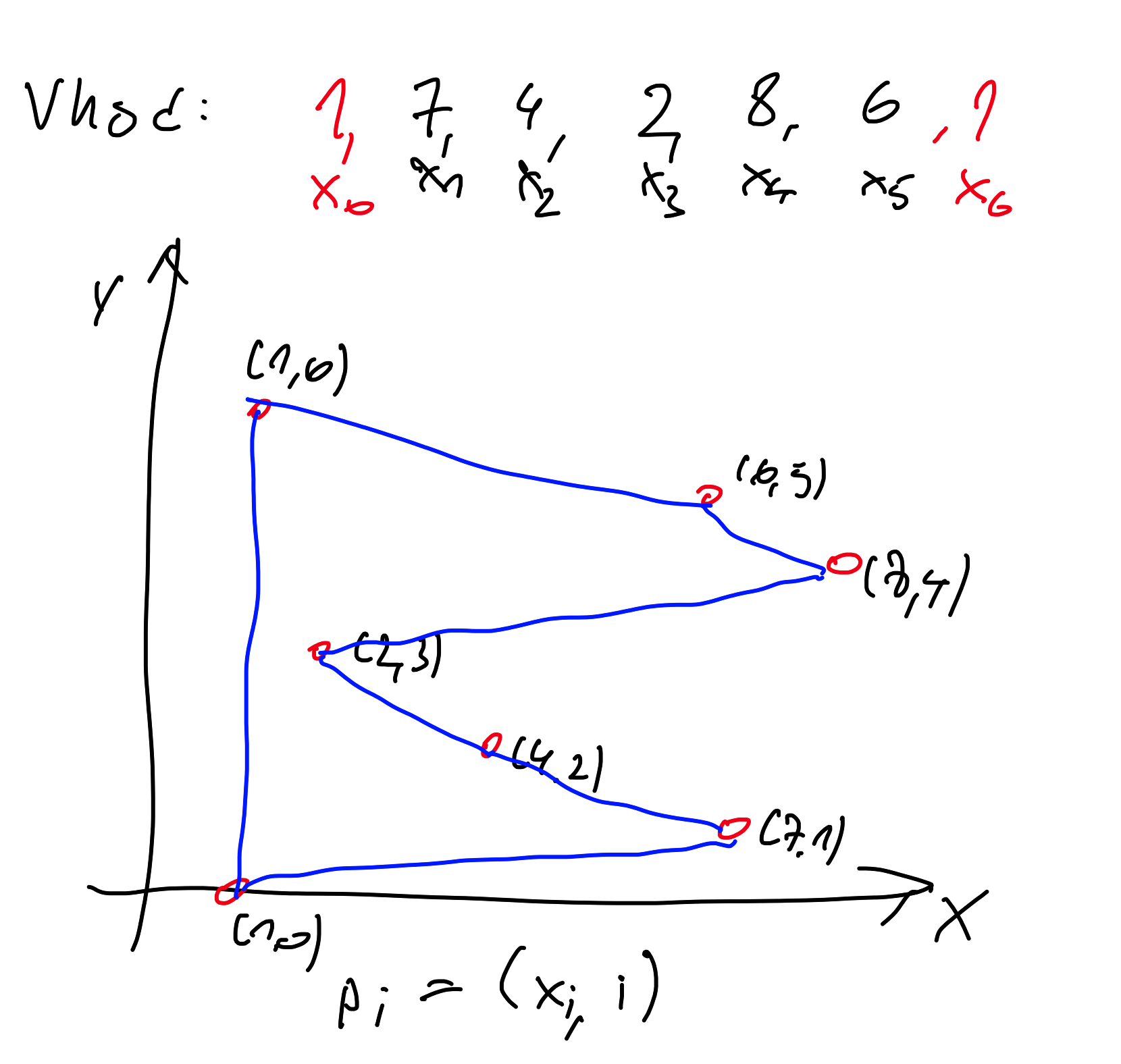
* Sestavimo večkotnik z oglišči $p_i = (x_i, i)$ ($0 \le i \le n+1$)
* Uporabimo naš algoritem, da dobimo zaporedje $q_0, q_1, \dots, q_{n+1}$ oglišč, urejenih po $x$
* Vrnemo $q_2.x, q_3.x, \dots, q_{n+1}.x$
* Časovna zahtevnost: $O(n)$

Tak algoritem potrebuje $\Omega(n \log n)$ - protislovje!


---

### Naloga 3

Opiši podatkovno strukturo za hranjenje konveksnega večkotnika $P$, ki omogoča, da v času $O(\log n)$ ugotovimo, ali je poizvedbena točka vsebovana v $P$. Konstrukcija podatkovne strukture mora biti izvedena v linearnem času.

----


Konstrukcija:
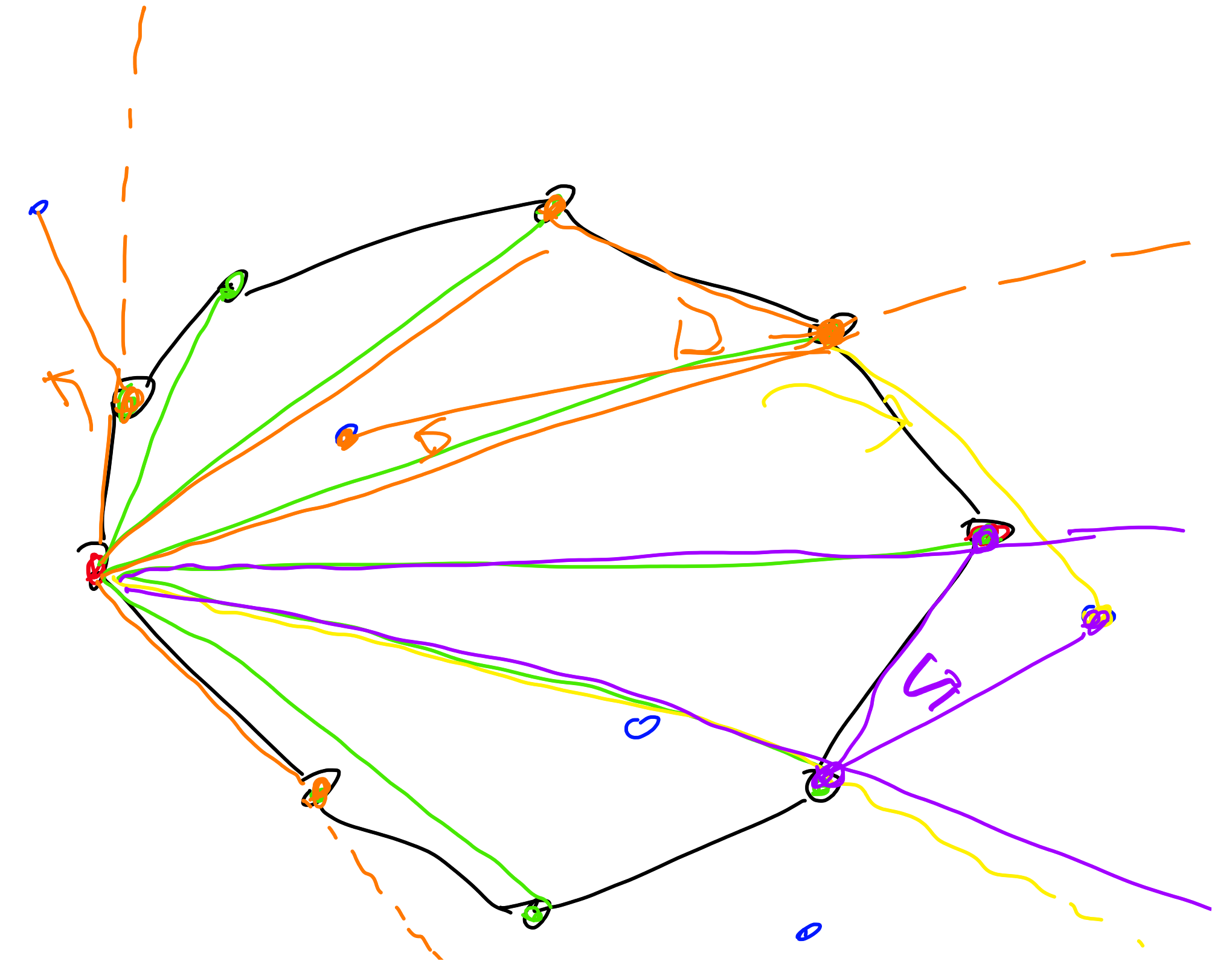
* Vhod: zaporedje oglišč $p_0, p_1, \dots, p_{n-1}$ v smeri urinega kazalca (če ni, obrnemo)
* Zapišemo $p_1, \dots, p_{n-1}$ v tabelo
* Časovna zahtevnost: $O(n)$

Poizvedba:
* Vhod: poizvedbena točka $q$
* Če je $p_0 p_1 q$ levi zavoj ali $p_0 p_{n-1} q$ desni zavoj, vrnemo $q \not\in P$
* Sicer izvedemo binarno iskanje: nastavimo $i := 1$, $j := n-1$
* Dokler $j - i > 1$, ponavljamo:
- Nastavimo $h := \lfloor {i + j \over 2} \rfloor$
- Če je $p_0 p_h q$ levi zavoj, nastavimo $j := h$
- Sicer nastavimo $i := h$
* Če je $p_i p_j q$ levi zavoj, vrnemo $q \not\in P$, sicer pa $q \in P$
* Časovna zahtevnost: $O(\log n)$

---

### Naloga 4

Podana sta dva konveksna večkotnika $P, Q$. Opiši algoritem, ki v linearnem času izračuna $\operatorname{CH}(P \cup Q)$. Če ne gre drugače, lahko predpostaviš, da sta $P$ in $Q$ disjunktna.

----


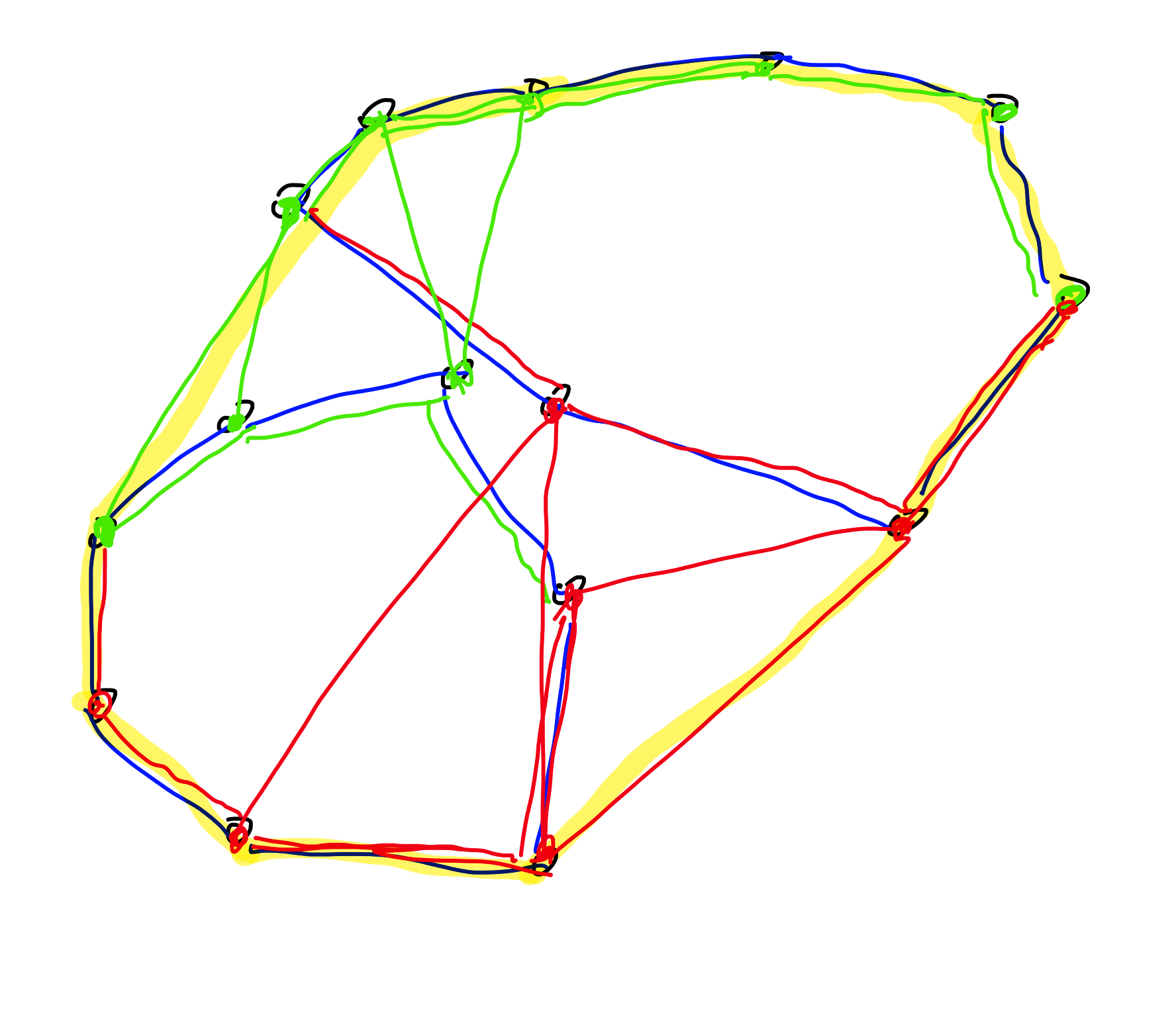
* Iz točk zgornjega/spodnjega dela $P$ in $Q$ s prirastnim algoritmom sestavimo zgornjo/spodnjo ovojnico $\operatorname{CH}(P \cup Q)$
* Časovna zahtevnost: $O(n)$
* Deluje tudi, če $P$ in $Q$ nista disjunktna!

---

### Naloga 5

Podan je konveksen večkotnik $P$ kot tabela (array) oglišč $p[1, \dots, n]$.

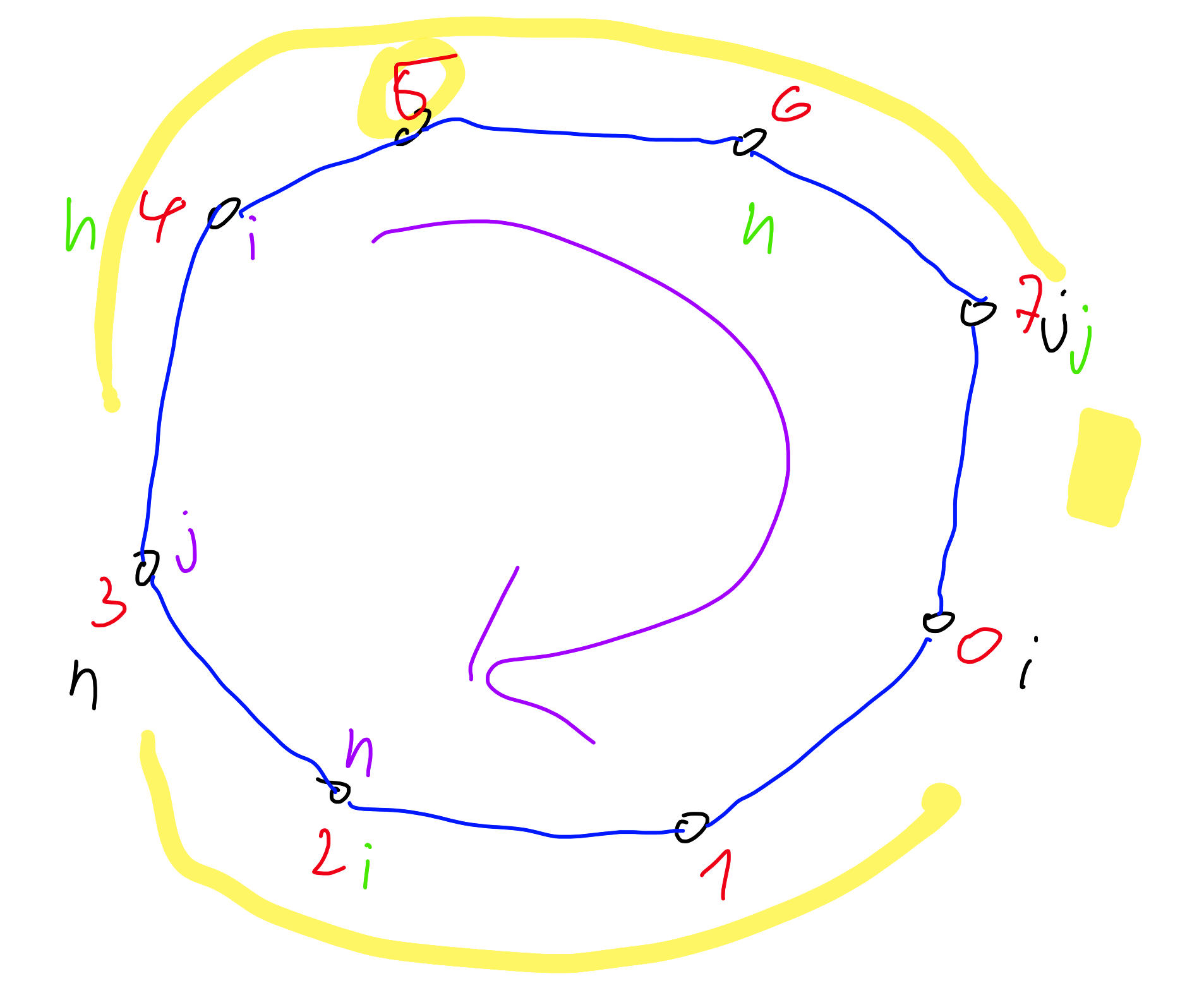
1. Opiši algoritem, ki v času $O(\log n)$ vrne najvišje oglišče iz $P$.
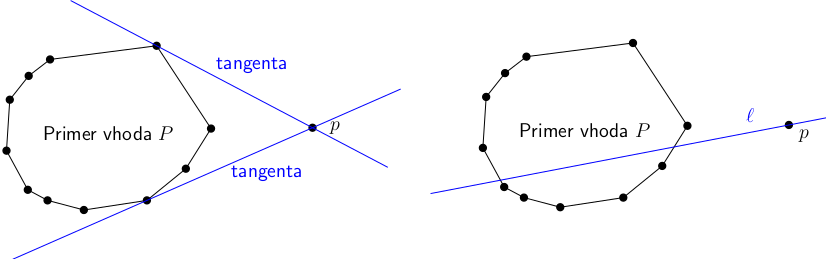
2. Opiši algoritem, ki v času $O(\log n)$ vrne obe tangenti večkotnika $P$
skozi podano točko $p\in \mathbb{R}^2 \setminus P$.
3. Opiši algoritem, ki v času $O(\log n)$ vrne presečišče med $P$ in podano premico $\ell$.
4. Opiši algoritem, ki v času $O(\log n)$ vrne točko iz $P$, ki je najbližja podani premici $\ell$.


----

1. ```python
def najvisja_tocka(p):
n = len(p)

def gor(i):
return p[(i+1) % n].y > p[i].y

i, j = 0, n-1
if gor(j) and not gor(i):
return p[i] # če je p[0] najvišja, bi jo v zanki zgrešili
while j - i > 1:
h = (i + j) // 2
if gor(i):
if gor(h) and p[h].y > p[i].y:
i = h
else:
j = h
else:
if gor(h) or p[h].y < p[i].y:
i = h
else:
j = h
if p[i].y > p[j].y:
return p[i]
else:
return p[j]

   ![](https://jaanos.github.io/computational-geometry/notes/2024-25/2024-11-28/binary-search.png)