---
tags: vaje, rg, večkotniki, konveksnost
hackmd: https://hackmd.io/x6II1iTmRG-e2818Db1TCg
plugins: mathjax
---
# Računska geometrija - vaje 21.11.2024

---

## Večkotniki

### Naloga 1

Večkotnik $P$ je *zvezden*, če obstaja točka $p \in P$, ki vidi cel večkotnik. Podana sta zvezden večkotnik $P$ in točka $p$, ki vidi cel $P$. Opiši algoritem, ki v linearnem času vrne triangulacijo večkotnika $P$.

----

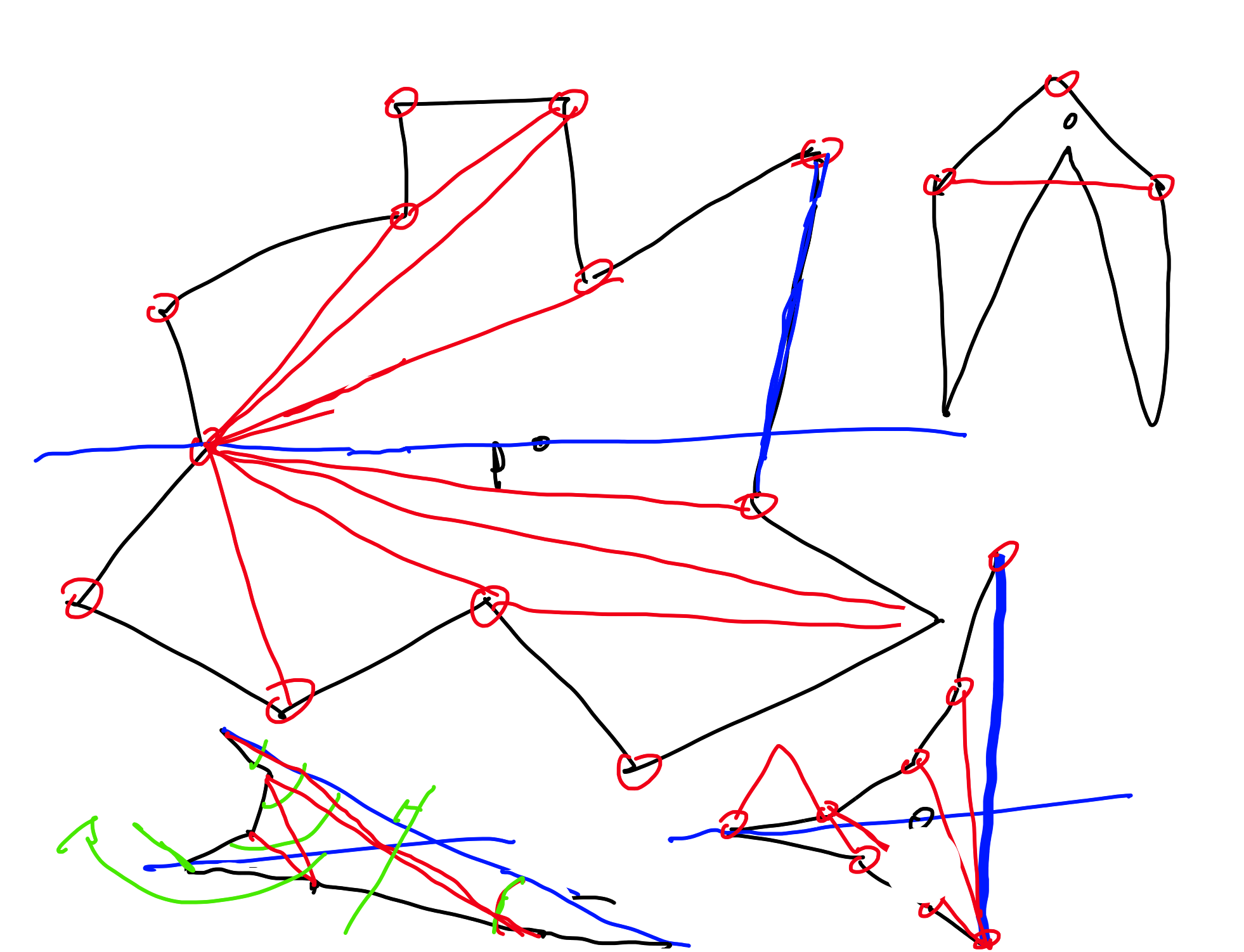
* potegnemo premico $\ell$ skozi $p$ in neko krajišče $w$, ta seka še neko stranico $uv$, tako da je $u$ nad $\ell$ in $v$ pod $\ell$
* z algoritmom za trianguliranje monotonih večkotnikov trianguliramo poti od $w$ do $u$ nad $\ell$ in od $w$ do $v$ pod $\ell$
* preostane večkotnik, ki ima vsa oglišča konkavna, razen $u, v, w$ - ta je monoton v smeri, pravokotni na $uv$, in ga trianguliramo
* algoritem teče v linearnem času


---

### Naloga 2

Opiši učinkovit algoritem za naslednji problem: podana sta večkotnik $P$ in notranja točka $p \in P$, nas pa zanima konstrukcija območja znotraj večkotnika $P$, ki je vidno iz točke $p$.

----


---

## Konveksnost

### Naloga 3

Dana je množica desetih točk ${\mathcal P} = \lbrace a,b,\dots, j \rbrace$. Za prirastni in Grahamov algoritem navedi trojice točk $(X, Y, Z)\in {\mathcal P}^3$, za katere algoritem preveri, ali je zaporedje $X,Y,Z$ zasuk na desno. V seznamu morajo biti trojice v istem vrstnem redu, kot jih algoritem preveri.



----



---

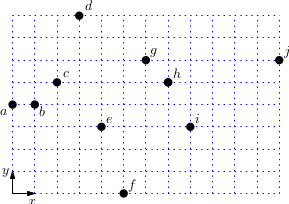
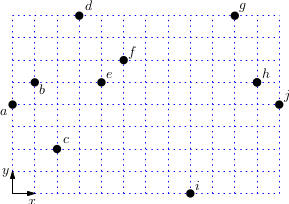
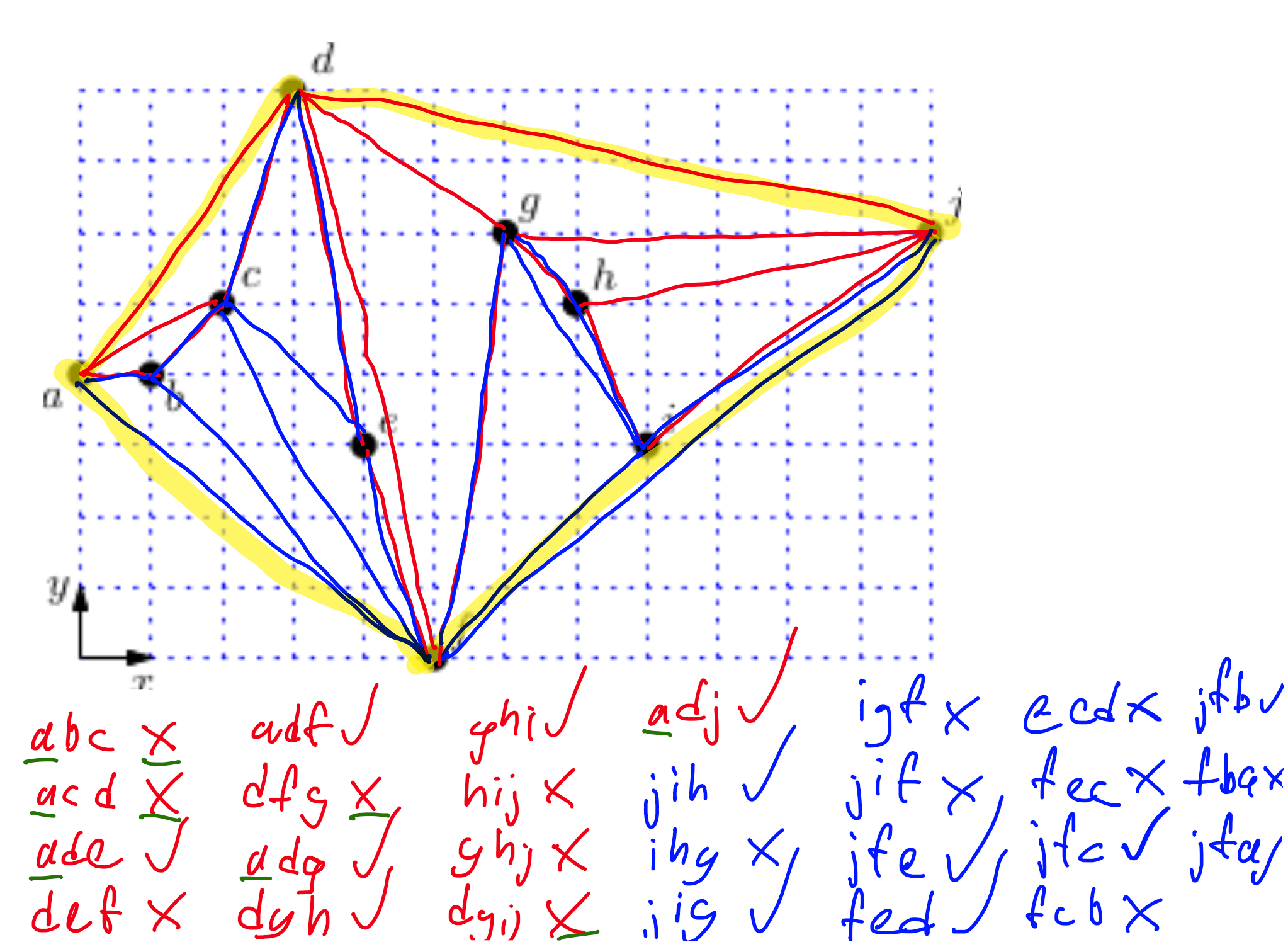
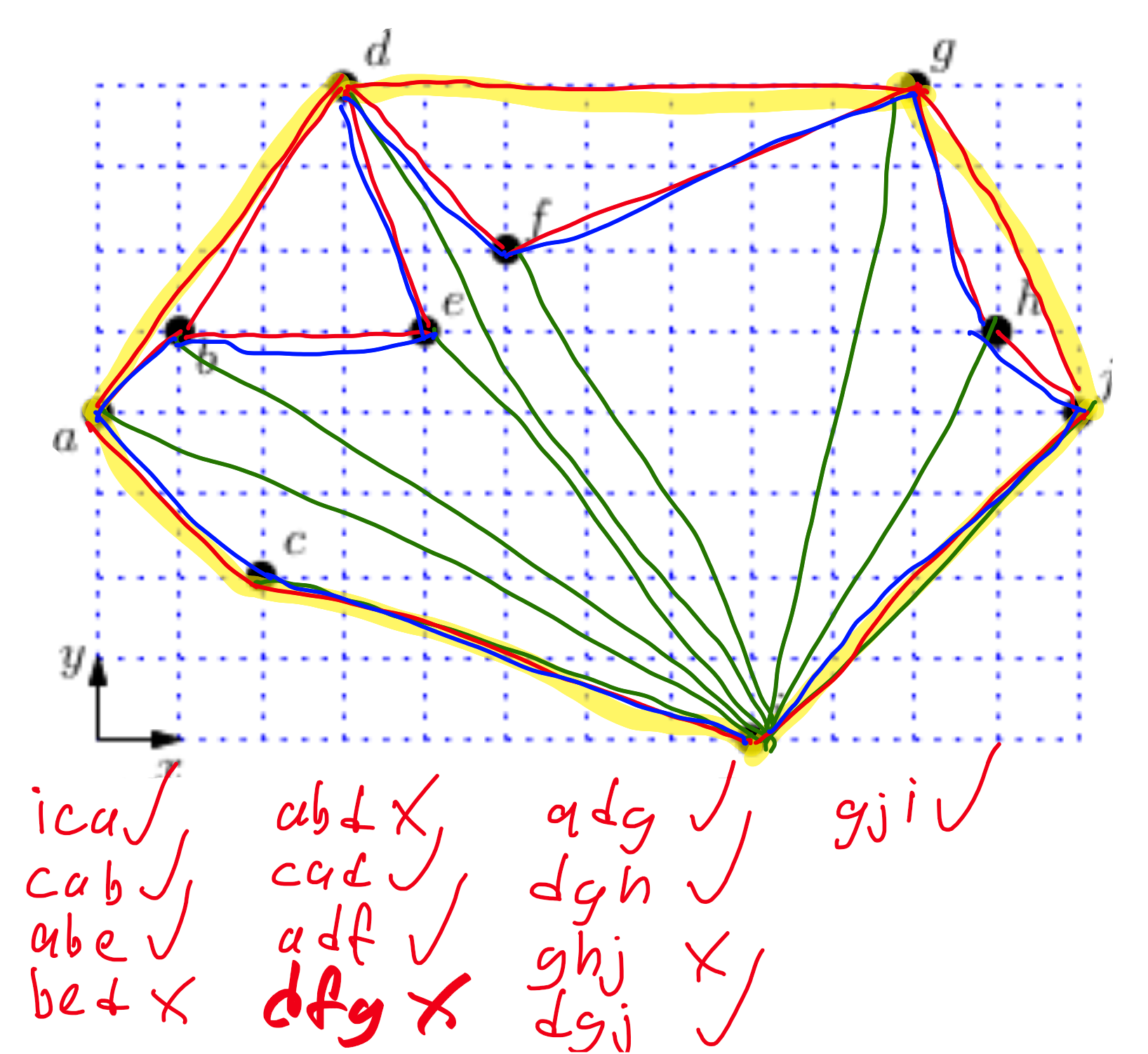
### Naloga 4

Za splošen $n$ opiši primer množice $n$ točk, v kateri vsaj ena točka nastopa v $\Omega(n)$ trojicah, ki jih prirastni algoritem preveri pri izračunu konveksne ovojnice.

----

$n$ točk postavimo na graf konveksne funkcije. Skrajno leva točka se pojavi pri $n-2$ trojicah pri izračunu zgornje ovojnice in se torej pojavi $\Omega(n)$-krat.


---

### Naloga 5

Grahamov algoritem je sestavljen iz dveh korakov:
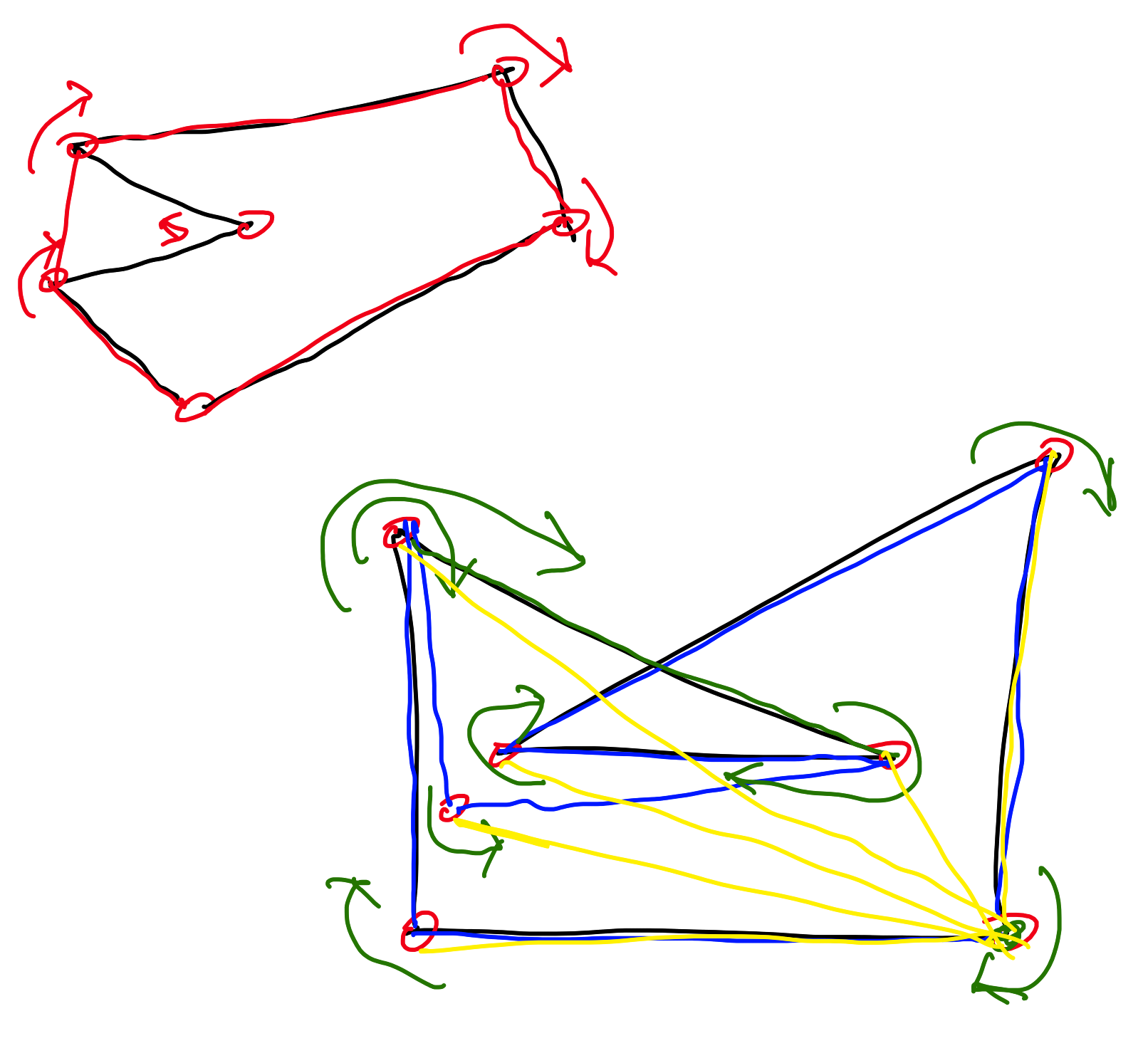
(1) iz podanih točk na določen način zgradimo večkotnik $M$ ter se nato (2) sprehajamo po $M$ in ga spreminjamo, dokler ne dobimo $\operatorname{CH}(P)$. Pokaži, da samo korak (2) ni dovolj za izračun konveksne ovojnice večkotnika: najdi tak večkotnik $N$, da ne dobimo $\operatorname{CH}(N)$, če na njem takoj izvedemo korak (2) Grahamovega algoritma.

----