owned this note
owned this note
Published
Linked with GitHub
---
tags: 嘉中資訊科培訓講義
---
# 嘉中資訊科培訓講義（intermediate level）
---
> [TOC]
---
## 一、資料結構再臨
### 持久化
有一顆線段樹，設它為root0，當我們要修改時，在別的記憶體空間開一個指標root1指向root0的子節點，遞迴進入子節點，若是此節點沒在修改的範圍內，就直接用指標指向他。
這樣的好處是，我們可以查詢歷史版本的線段樹，比如在經過五個修改後，查詢第2版的線段樹。
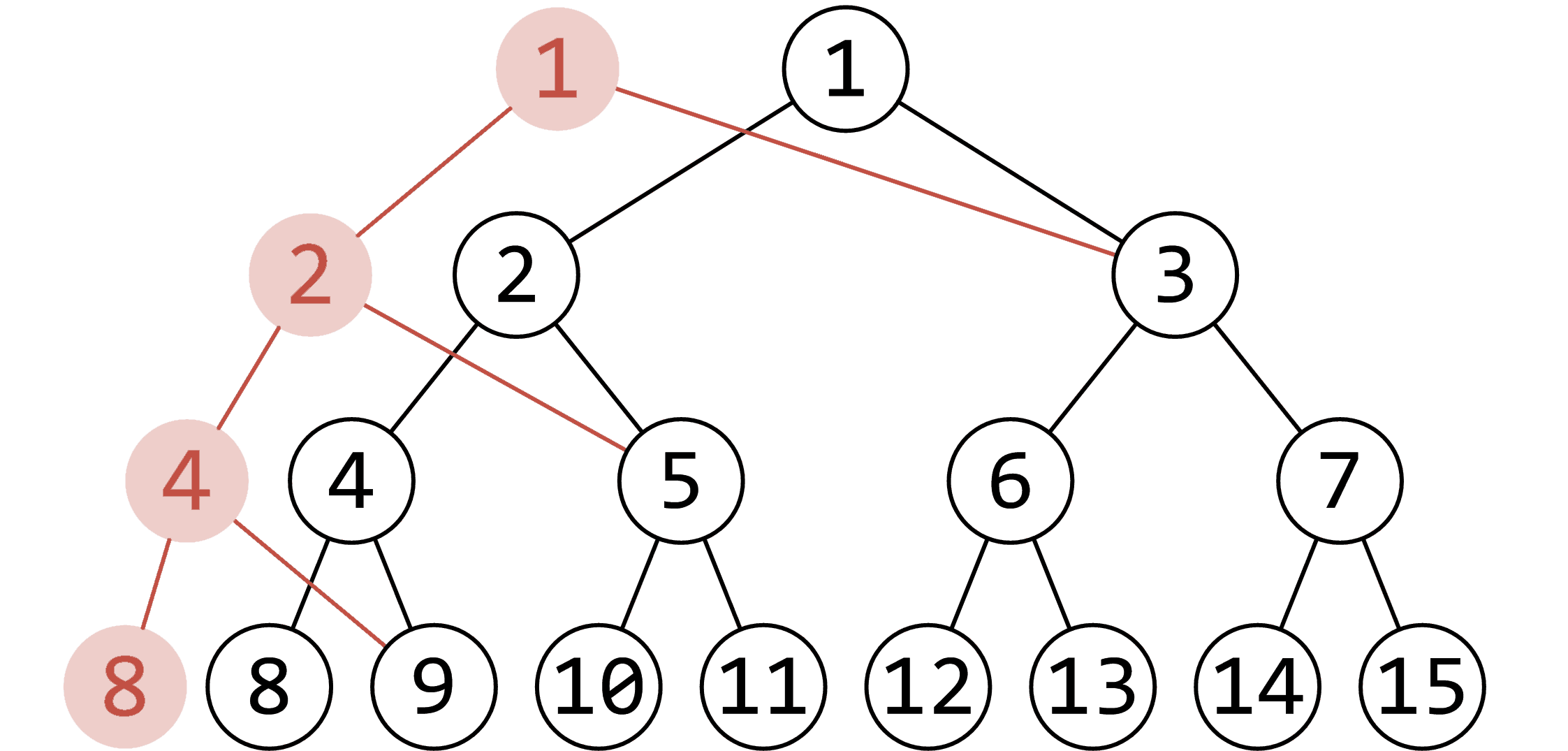
當然，空間複雜度會變大，至於究竟開多大?
差不多$4*N+QlogN$就好，正負多少自己斟酌一下(?。
但是時間複雜度還是保持一樣。 可以想想看為什麼。
幾乎所有持久化結構都是用這種 __路徑複製__ 的方式去實現。
練習題: [zj b405](https://zerojudge.tw/ShowProblem?problemid=b405)
### zkw線段樹
不用遞迴處理的線段樹，常數比線段樹小，也比較快。
很少用到。
__build__
```cpp=
for (M = 1; M < N; M <<= 1);
for (int i = M + 1; i < M + 1 + n; ++i) cin >> tree[i];
for (int i = M - 1; i; --i)
tree[i] = maintain(tree[lson(i)], tree[rson(i)]);
```
__query__
```
```
__modify__
```
```
__interval modify__
```
```
---
## 二、圖論
### LCA
> 應該不用我再講題目了?
#### 樹上尤拉序列
#### Tarjan
### 樹分治
#### 樹鏈剖分
> 給定一顆樹，上面有$n$個節點，每個節點都有顏色$c$
> 現有兩操作，
> 1. 修改點$p$的顏色為$b$
> 2. 詢問點$p$到$q$的路徑上總共有幾種顏色
>
> $c \leq 60, n \leq 2\times 10^5$
與初級講義的[某一題](https://codeforces.com/problemset/problem/620/E)是否有些類似?
但是這裡是詢問一條路徑，而非一個子樹，但是相同的，我們也可以用dfs序來維護樹上的資訊。
如果我們把樹拆成一條一條的"鍊"，
那或許就有好的方法來維護樹上資訊了。
- __輕重鍊剖分__
對於每個節點都有其子樹節點的數量$sz_i$，在一個節點$i$找出其子樹$max\{sz_j, j\in i\}$，選擇他當作現在這個重鍊的下一個點，而其餘子樹各自繼續成為一個鍊。
很難描述，直接上code:
```cpp=
void findHeavySon(int32_t now, int32_t pa) //維護sz[], fa[], dep[]的code省略
{
pair<int32_t, int32_t> heavy = {-1, -1};
for (auto nex : Son[now])
{
if (nex == pa) continue;
findHeavySon(nex, now);
heavy = max(heavy, {sz[nex], nex});
}
heavySon[now] = heavy.second;
}
void buildChain(int32_t now, int32_t pa, int32_t chainTop)
{
dfn[now] = cnt++;
ChainTop[now] = chainTop;
buildChain(heavySon[now], chainTop);
for (auto nex : Son[now])
{
if (nex == pa || nex == heavySon[now])
continue;
buildChain(nex, now, nex);
}
}
```
現在我們可以用這些鍊來處理樹上問題了，比如說LCA:
先判斷兩個點是否在同一條鍊上，若是，答案則為深度最淺的點。
若否，則將兩點中深度較深的點不斷往上丟到鍊首的父親節點。
```cpp=
int32_t lca(int32_t a, int32_t b)
{
while(ChainTop[a] != ChainTop[b])
{
if (dep[a] < dep[b])
swap(a, b);
a = fa[ChainTop[a]];
}
return dep[a] > dep[b] ? b : a;
}
```
而其實在詢問LCA的過程，就找到了那條唯一的路徑，所以我們可以使用dfs序來處理一條鍊的問題。
以最上面的問題為例:
```cpp=
int32_t query(int32_t a, int32_t b)
{
int64_t ans = 0;
while(ChainTop[a] != ChainTop[b])
{
if (dep[ChainTop[a]] < dep[ChainTop[b]])
swap(a, b);
ans |= ask(dfn[ChainTop[a]], dfn[a]);
// 可以用線段樹等，可支援區間查詢的data structure來維護。
a = fa[ChainTop[a]];
}
if (dep[a] > dep[b])
swap(a, b);
ans |= ask(dfn[a], dfn[b]);
return countOne(ans);
}
```
- __複雜度__:
__build:__ $O(n)$
__query LCA:__ $O(log n)$
__query + data structure:__ often $O(log^2n)$
練習題: (待補)
---
#### 重心剖分
> 給定一顆樹，上面有$n$個節點，每條邊都有其權值$w$，求有幾個點對距離不大於$k$
> $n\leq 10^5$
>
以樹重心為根節點則有最小的最大子樹
* __找樹重心能幹麻？__
顯然，若樹重心有最小的最大子樹，那我們可以大膽claim，他的子樹最大深度為$\dfrac{|V|}{2}$
這是個非常優秀的性質，仔細觀察就能發現，如果我再從子樹裡找子樹的樹重心，不斷做到葉節點，那顯然可以把原始的樹變成深度最多為$log(|V|)$的樹
但是這種作法會破壞原本樹的形狀，因此這種作法通常只會用在—樹DP或者其他可以樹上分治的題目
* __實作與應用__
---
### 二分圖
---
## 三、字串
### Miller-Rabin
### Trie
### AC自動機
## 四、分塊
## 五、數論
### 歐拉公式
> エミリア的數學老師說這根本不用證明，直覺無比。
對於任意正整數$a,n,p$皆滿足
$a^{\varphi(n)+p \%\varphi(n)} \equiv a^p \pmod n$
> 沒有$gcd(a,n)=1$的限制了:)
> ~不用這個公式要化簡指數，當然也可以~
> ~只要把n拆成與a互質的數，然後用中國餘數定理噁心的組裝回來就可以了www~
---
### 漸進數列
在一般m項的漸進數列$a_{n} = b_1a_{n-1} + b_2a_{n-2}... + b_ma_{n-m}$，可以改成
$\begin{bmatrix}
b_1 & ... & b_{m-1} & b_m \\
1 & ... & 0 & 0 \\
0 & ... & 0 & 0 \\
0 & ... & 1 & 0 \\
\end{bmatrix}
\begin{bmatrix}
a_{n-1} \\
a_{n-2} \\
a_{n-3} \\
... \\
a_{n-m}
\end{bmatrix}=
\begin{bmatrix}
a_{n} \\
a_{n-1} \\
a_{n-2} \\
... \\
a_{n-m+1}
\end{bmatrix}$
這裡貼心的替你做了整理，當我們要求數列第$n$項時，只需將$\begin{bmatrix}
b_1 & ... & b_{m-1} & b_m \\
1 & ... & 0 & 0 \\
0 & ... & 0 & 0 \\
0 & ... & 1 & 0 \\
\end{bmatrix}$
連乘$n-1$次，接著把最下面那一排乘上一開始的數字$a_{m}, a_{m-1}...a_1$再加起來就好了。
例子:
$a(n) = a(n - 1) + 2a(n - 2), a(1) = 1, a(2) = 3$
求第$4$項?
$$
\begin{bmatrix}
1 & 2 \\
1 & 0 \\
\end{bmatrix}^3 =
\begin{bmatrix}
5 & 6 \\
3 & 2 \\
\end{bmatrix}
$$
$$
\begin{bmatrix}
5 & 6 \\
3 & 2 \\
\end{bmatrix} \times
\begin{bmatrix}
3 \\
1 \\
\end{bmatrix}=
\begin{bmatrix}
21 \\
11 \\
\end{bmatrix}
$$
__ans: 11__
code: 待補。
#### 非齊次數列
---
### 離散對數
> 請找到一數$x$，滿足$a^x \equiv 1 \pmod p$
>
基本上也沒有什麼好的算法，最常被使用的就是小步大步算法(baby step, giant step)
複雜度: $O(\sqrt p)$
---
### RSA
---
## 六、DP
### 滾動
---
### 斜率優化
* 用法
通常dp轉移式會像這樣$dp[i] = g(i) + max_{j<i}(a[j]*x[i] + b[j])$
$a[j]、b[j]$可以是包含$dp[j]$的式子（反正就是與j有關的）
這時可以觀察到max裡面的式子長的像斜截式。一條$a[j]$為斜率，$b[j]$為截距的方程。那我們要找出在x座標為$x[i]$情況下，最大的y值。
練習題: [hdu3507](http://acm.hdu.edu.cn/showproblem.php?pid=3507)(經典題), [luogu P4072](https://www.luogu.com.cn/problem/P4072)
* 單調隊列優化
接續剛剛斜率優化的思維，如果x[i]是個單調遞增的東西，那就可以是非常簡單的DP了><
我們可以考慮這樣的一個情況。
在一個queue裡儲存著所有可能轉移到i的數，那對於一個新加入queue的j若j的轉移優於已經在queue裡的k，則必有以下關係
$a[j]*x[i]+b[j]>=a[k]*x[i]+b[k]$
$=> x[i]*(a[j]-a[k])>=b[k]-b[j]$
$=> x[i]>=\dfrac{b[k]-b[j]}{a[j]-a[k]}$
//若a[j]-a[k]<0要變號，那x[i]要是單調遞減的數，才能單調隊列優化
顯然對於未來任意的x[i]都能同樣保持j優於k的性質（因為x[i]單調遞增）
因此可以將k永遠踢出queue
> 你可以把這想像成在維護一個下凸包
實作上需要為了確定queue.front()是i的最佳轉移，要queue[0]和queue[1]比較，每個新加入queue的數也須要與隊尾比較
實作上也常用deque或自己實作deque方面同時處理隊首與隊尾
```cpp=
//踢隊頭
while(r>l && slope(dq[l],dq[l+1])>x[i])
++l;
// dp[i] get!
dp[i]=a[l]*x[i]+b[l];
//踢隊尾
while(r>=l && slope(dq[r-1],i)<slope(dq[r-1],dq[r]))
--r;
//放入
dq[++r]=i;
```
### Aliens優化
### 四邊形優化
### 虛樹
## 七、離線算法
### 莫隊算法
#### 樹上莫隊
### CDQ分治
### 整體二分
## 八、隨機演算法
當你覺得題目很難，然後又感覺題目可能有一些神奇的性質，或許你可以考慮看看，不失為一個喇分的好方法。
### color coding
## 九、思維題
### 構造題
例題：zerojudge f008
Google Drive
Gist
Clipboard
Sign in with Wallet
