# Tensor Core

## Background
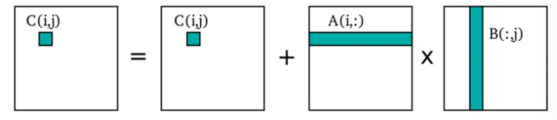
Matrix multiplications lie at the heart of Convolutional Neural Networks (CNNs). Both training and inferencing require the multiplication of a series of matrices that hold the input data and the optimized weights of the connections between the layers of the neural net.

The Tesla V100 is NVIDIA's first product to include tensor cores to perform such matrix multiplications very quickly. Assuming that half-precision (FP16) representations are adequate for the matrices being multiplied, CUDA 9.1 and later use Volta's tensor cores whenever possible to do the convolutions. Given that very large matrices may be involved, tensor cores can greatly improve the training and inference speed of CNNs.

## Evolution of Tensor Core
Ampere Tensor Cores introduce acceleration for sparse matrix multiplication with fine-grained structured sparsity and a new machine learning data type called bfloat16 (BF16).

Ampere Ar-chitecture redesigns the micro-architecture of Tensor Cores.

## What?
> Aiming for higher throughput for GEMM( General Matrix Multiply)
> 使用較低精度的 FP16 進行 MMA(matrix multiply-and-accumulate) 運算，讓加速運算速度的同時，又能夠最小化對於模型精準度的負面影響

The Tensor Core is
- A fast hardware functional block for dense matrix multiplication (inner-product)
- 

- A specialized cores that enable mixed precision training
- Capable of performing **4 x 4 matrix multiply-and-accumulate (MMA)** operations, which are a series of multiplications and additions performed on arrays of numbers (matrices)
- These operations are fundamental to the calculations for neural network training and inference.

- When?
- It was first introduced in NVIDIA’s Volta architecture .
- Advantage?
- Highly efficient
- Provide a significant speedup for tasks that involve a large number of such matrix operations, which is typical in deep learning computations, such as the training and inference phases of neural networks.
- Traditionally, the multiplication and addition would be separate operations, which would require more computational cycles and would involve storing intermediate results.
- Problems?
- Sparse Matrix
- The cost of excessive computation of DNN due to the over-provisioned parameter space, reducing efficiency
- [Sparse Tensor Core: Algorithm and Hardware Co-Design for Vector-wise Sparse Neural Networks on Modern GPUs](https://docs.google.com/presentation/d/1JmWpPJ8TDDdprFiVJbQRrRaSkS7sc3fXiLZIY5Jp1UM/edit?usp=sharing)
- Current mma API vs legacy wmma API
- wmma APIs support fewer operand shapes and can not leverage the new sparse matrix multiplication feature of the newest Ampere Tensor Core

### Tensor Core inside SM

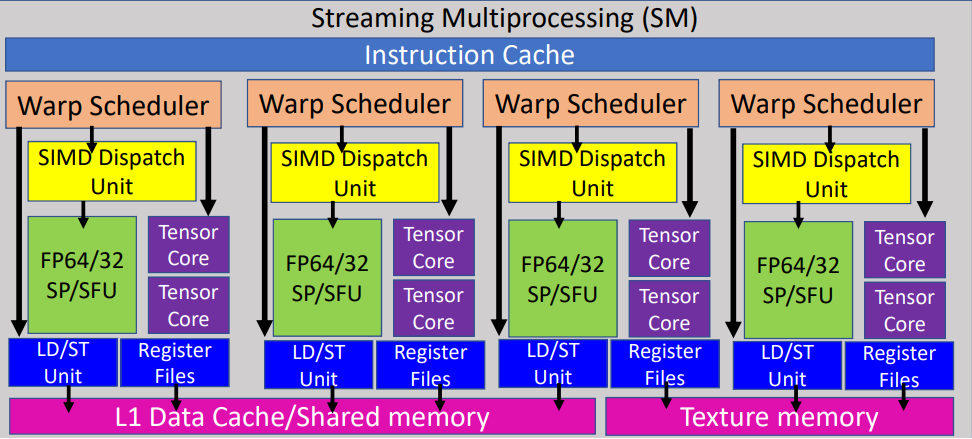
- An SM consists of four subcores.
- Each SM consists of four warp schedulers or four sub-cores to issue four warp instructions simultaneously
- In each subcore, there is a warp scheduler, a math dispatch unit, streaming processor arrays for multiple data types (a.k.a. CUDA Cores), special function units (SFUs), two Tensor Cores, LD/ST unit, and register files.
- Tensor Cores use the same memory hierarchy as CUDA cores.
- Both Tensor Cores and CUDA cores can fetch data through direct addressing ( `ld` instruction) from the Shared Memory or global memory via the **per-thread** scheme
- Per-thread means the instruction is executed by a single thread independently; both behavior and result of the thread are deterministic.
- Tensor Cores have two special load instructions – recent `ldmatrix` and legacy `wmma:load` via the **per-warp** scheme
- Per-warp means the instruction is executed by the 32 threads within the same warp cooperatively; neither behavior nor the result of individual thread is deterministic.
- The L1 data cache and shared memory are shared among the four subcores within the SM.
### Tensor Core Architecture

#### How a WMMA operation is mapped to the Tensor Core architecture
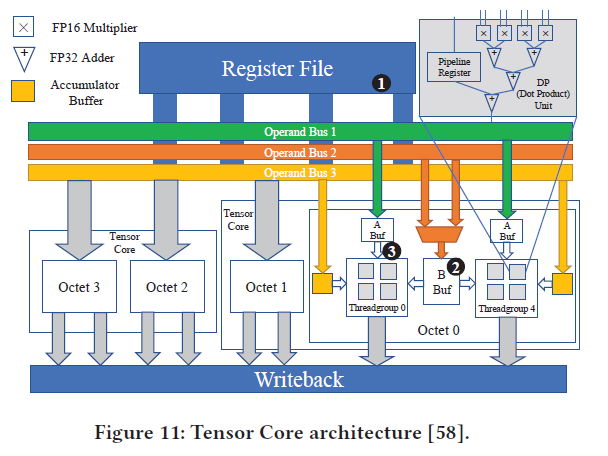
1. There are **2 octets** in a Tensor Core.
1. Inside an octet, there are **8 dot product (DP) units**, each of which can compute a <u>4-dim vector dot product per cycle</u>.
2. **1 worktuple** is mapped to **1 octet** and thus each threadgroup takes four DP units
3. one set of HMMA instructions 是由 1 個 worktuple 處理
2. The octet has <u>operand buffers</u> to feed the worktuple via the tiled data when executing one set of HMMA instructions.
1. Each threadgroup has dedicated operand buffers for Operand A and Operand C.
2. **Each operand buffer can hold a 4×4 tile**.
3. **The operand buffer dedicated to operand B can hold a 4×8 tile** and the data inside are shared by the two threadgroups in the same worktuple
3. **One threadgroup** computes the multiplication of a 4×4 tile by a 4×8 tile in **a set of HMMA instructions**, which is 4×8=32 4-dim dot products. (總共需要 32 次內積運算)
1. Because **4 DP units compute 4個 4-dim vector dot products per cycle**, those set of HMMA instructions require at least 8 clock cycles to finish the computing of the 4×8×4 matrix multiplication

## How?

### 基本功能
- **Each Tensor Core is able to execute a 4×4×4 MMA (matrix multiplication and addition) in one cycle.**
- Why does tensor core use 4 x 4 matrix ?
- 為了對應 `threadgroup` 的分法?
- tile的大小以M×N×K表示，A的維度是M×K，B的維度是K×N，C和D的維度是M×N。
- A => 4 x 4
- B => 4 x 4
- C => 4 x 4
- The Tensor Core in Volta GPUs provides **2 execution modes**
- **FP16 Mode**: In this mode, the Tensor Core **reads three 4x4 FP16 matrices** as input and performs operations on them.
- This mode uses 16-bit floating-point matrices, which are smaller and require less computational power than higher precision formats.
- **Mixed-Precision mode**: This mode enables the use of both 16-bit and 32-bit floating-point matrices. It reads two 4x4 16-bit matrices and pairs them with a third 4x4 32-bit matrix for accumulation. This approach balances the need for speed (with 16-bit operations) and precision (with 32-bit accumulation) to improve the performance and accuracy of the computations.


**內部零件:**


### 程式和架構運行
- 2 Tensor Cores are used concurrently by a warp
#### How does Tensor core operate
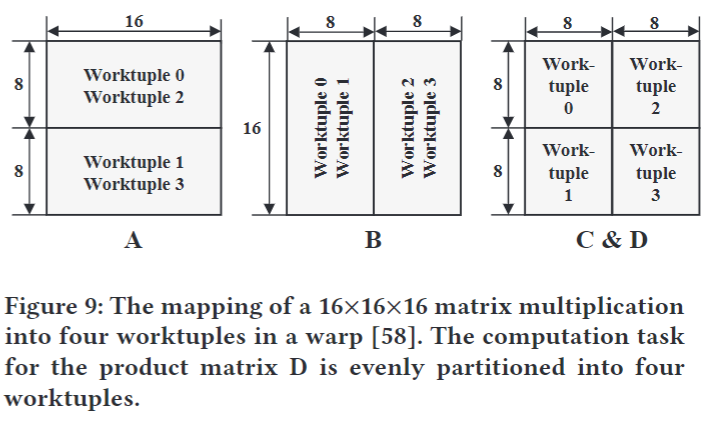
- 32 threads within a warp collaborate to conduct the 16×16×16 matrix multiply and accumulate operation efficiently
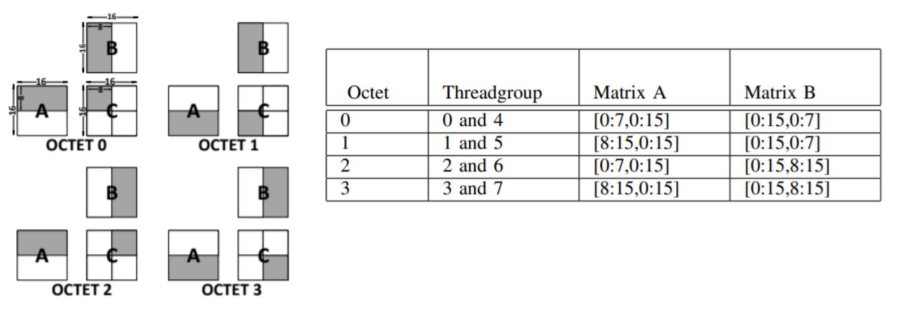
- To execute a WMMA, the 32 threads in a warp are divided into **8 threadgroups**.
- Each threadgroups has 4 threads
- All threads in a threadgroup work together to compute 4×4 tile multiplications
- For better data reuse, **2 threadgroups** work together as  **a worktuple**.
- Each **worktuple** is responsible for computing 一個 8×8 tile of D
- Worktuple i consists of threadgroup i and threadgroup i + 4.
- Thethreadgroup Id of a given thread is  $$\left\lfloor \frac{\text{threadId}}{4} \right\rfloor.$$
Each worktuple is responsible for com-puting one 8×8 tile of D.
- For example, Worktuple 0 ( threadgroups 0, threadgroups 4) computes `D[0:7,0:7]`
- To achieve this, Worktuple 0 multiplies `A[0:7,0:15]` and `B[0:15,0:7]`, adds the product 8×8 tile with `C[0:7,0:7]`, and saves the result to `D[0:7,0:7]`.


#### Compilation
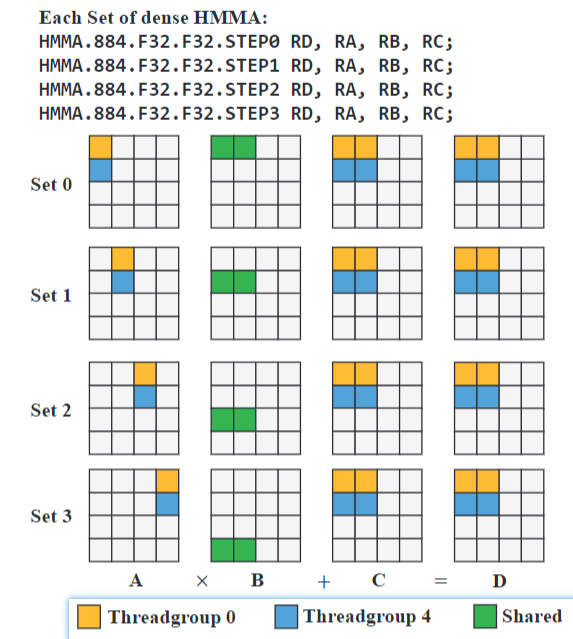
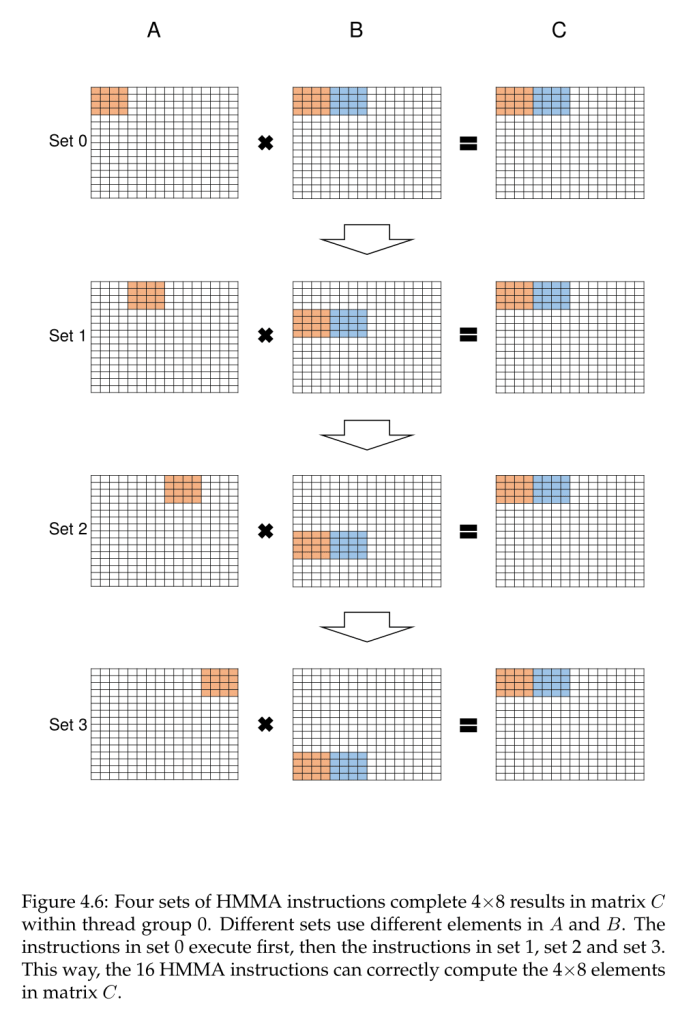
- During the compilation time, a WMMA operation breaks down into 4 sets of machine-level HMMA instructions
- In the mixed precision mode, each set of HMMA instructions computes the product of a 4×4 tile of A and a 4×8 tile of B.
- The 2 threadgroups in Worktuple 0 share a 4×8 tile of B in each set.
- The 4×4 tiles of A are private to the threadgroups.
- The four sets of HMMA instructions of Threadgroup 0 and 4 compute the product submatrices `D[0:3 ,0:7]` and `D[4:7 ,0:7]`

### Programming API
In the CUDA programming model , Tensor Cores are exposed to programmers in the **CUDA WMMA(Warp Matrix Multiply and Accumulate) API**.
- The WMMA API includes dedicated **matrix load and store** primitives, and **matrix multiply and accumulate** operations for Tensor Cores.
- The WMMA matrix load and store operations are designed for moving data between register files and the memory hierarchy

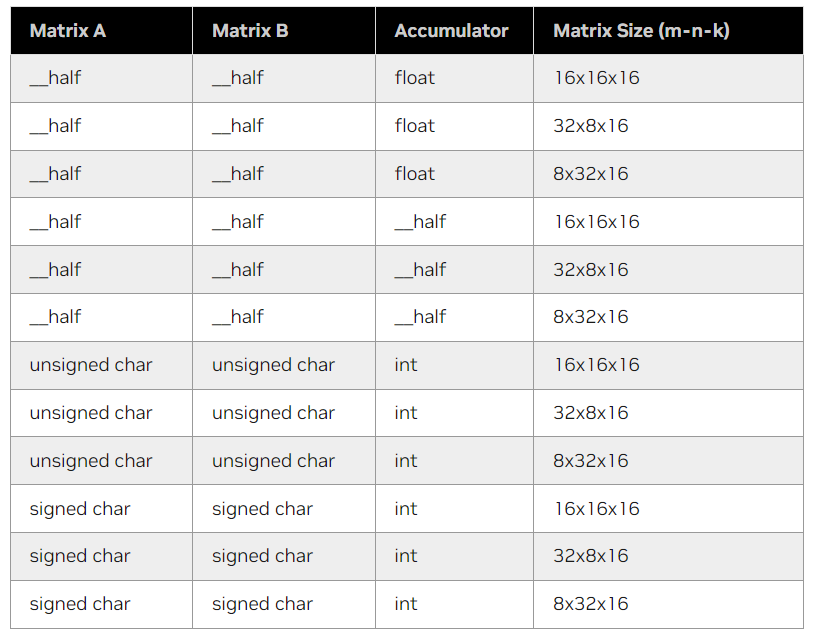
WMMA API in CUDA 12.2
- Support various tile size combination

名詞解釋
- `tile`: A sub-section or block of a larger matrix that is processed as a unit by the GPU
- **Warp Execution on Tile**: A "warp" is a group of threads that execute in lockstep on a GPU. A warp in NVIDIA's CUDA platform typically consists of 32 threads. When a warp is executing a matrix operation using Tensor Cores, it operates on a "tile" of the matrix. This tile is a submatrix or block of the larger data set that is being processed.
- Advantage:
- Processing matrices in tiles is beneficial because it allows the workload to be divided among multiple processing units (like Tensor Cores), enabling parallel computation. It also helps to fit the computation within the fast, but limited, shared memory space available to the GPU's multiprocessors.
- `fragment`: A data structure that holds a part of the tile data
- A concept that is specific to NVIDIA's WMMA (Warp Matrix Multiply-Accumulate) API for Tensor Cores
- **Fragment in Registers**: A "fragment" is a portion of the tile that each thread or a group of threads in the warp works on. Fragments are small enough to fit into the fast-access register memory of the individual threads. This allows each thread to quickly access and process its assigned portion of the tile.
- Advantage:
- By breaking a tile into fragments, the WMMA API enables fine-grained parallelism where each thread in a warp can work on its own fragment. This allows the Tensor Cores to be used efficiently since each core can process multiple fragments simultaneously

To put it into the flow of execution:
1. The larger matrix is divided into tiles that are appropriate for processing by the warp's Tensor Cores.
2. Each tile is then broken down into fragments.
3. The fragments are loaded into the registers of the threads in the warp.
4. The warp's Tensor Cores perform the matrix operations on these fragments in parallel.
5. The results are then written back to the main memory or used in further computations as required.

template<typename Use, int m, int n, int k, typename T, typename Layout=void> class fragment;

void load_matrix_sync(fragment<...> &a, const T* mptr, unsigned ldm);
void load_matrix_sync(fragment<...> &a, const T* mptr, unsigned ldm, layout_t layout);
void store_matrix_sync(T* mptr, const fragment<...> &a, unsigned ldm, layout_t layout);
void fill_fragment(fragment<...> &a, const T& v);
void mma_sync(fragment<...> &d, const fragment<...> &a, const fragment<...> &b, const fragment<...> &c, bool satf=false);

`fragment`：Tensor Core資料儲存類，支援matrix_a、matrix_b和accumulator
`load_matrix_sync`：Tensor Core資料載入API，支援將矩陣資料從global memory或shared memory載入到fragment
`store_matrix_sync`：Tensor Core結果儲存API，支援將計算結果從fragment儲存到global memory或shared memory
`fill_fragment`：fragment填滿API，支援常數值填充
`mma_sync`：Tensor Core矩陣乘計算API，支援D = AB + C或C = AB + C

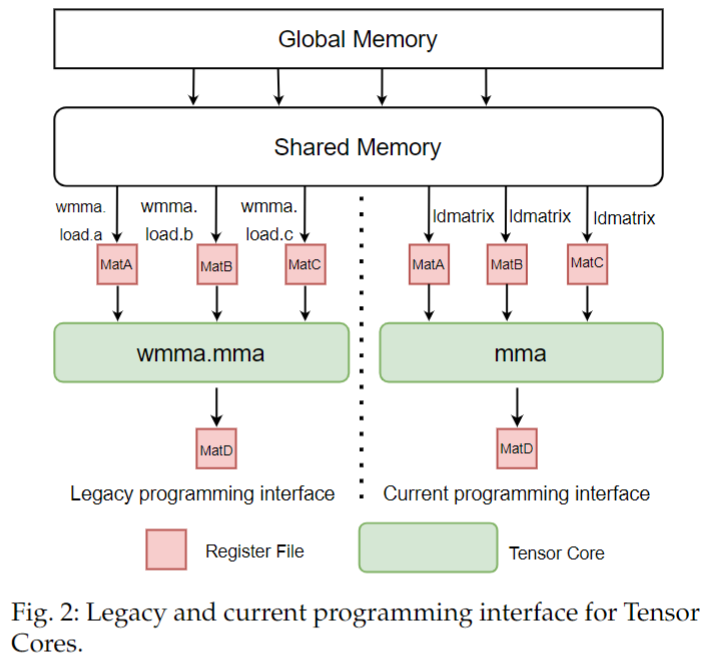
The programming of Tensor Cores has also evolved over the generations. Figure 2 illustrates the legacy and current programming interface for Tensor Cores. The first step is to load data from Shared Memory to the Register File and then use Tensor Cores to accelerate the matrix computation.

Legacy wmma interface was introduced with first-generation Volta Tensor Cores.
In gen-eral, the legacy wmma programming interface can satisfy basic usage of Tensor Cores and requires less programming efforts, because wmma.load can help manage the special input operand storage layout in the Register File for Ten-sor Cores.
- However, wmma instructions can only leverage limited features of the Tensor Cores.
- Specifically, it **can not use sparse acceleration and has fewer choices of the matrix operand shape**.
- Furthermore, wmma.load instruc-tions have more strict requirements for the data layout in Shared Memory.

By contrast, the new programming interface provides access to all features of the Tensor Cores (i.e. more matrix operand shapes and novel sparse acceleration). The vendor’s library CUTLASS also chose the new programming interface as the underlying implementation for the best possible perfor-mance.

Therefore, users should use the new programming interface when seeking for best possible performance or exploiting the new sparse acceleration feature

#### differences between legacy wmma.mma and current mma PTX instruc-tions

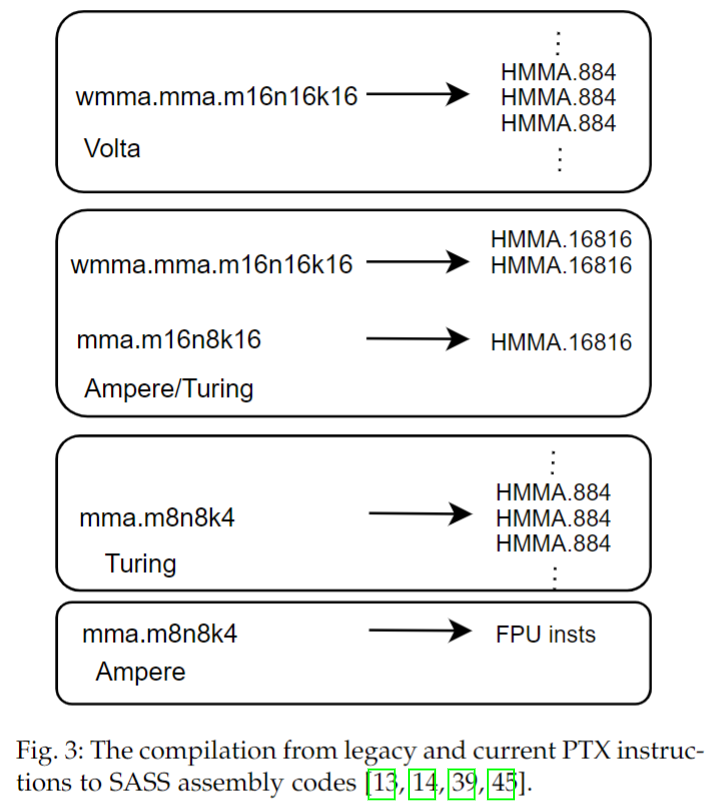
## MMA, FMA, GEMM
MMA (Matrix Multiply and Accumulate) and FMA (Fused Multiply-Add) are two types of arithmetic operations that are optimized in modern processors to perform computations efficiently, but they operate on different scales and are used in different contexts.

| Feature/Operation | Fused Multiply-Add (FMA) | Matrix Multiply and Accumulate (MMA) | General Matrix Multiply (GEMM) |
|-------------------|--------------------------|--------------------------------------|-------------------------------|
| **Scale** | Individual floating-point numbers | Matrices (e.g., 4x4 matrices) | Matrices of any size |
| **Operation** | Performs a single multiply-add operation: <br>result = a x b + c | Involves matrix multiplication followed by addition to an accumulator matrix D = A x B + C| Performs matrix-matrix multiplication followed by matrix addition: <br>C = $\alpha$ A x B + $\beta$ C |
| **Purpose** | Reduces rounding errors and increases performance for high precision computations | Accelerates machine learning and graphics by optimizing matrix operations | Generalized operation for linear algebra computations across various applications |
| **Hardware** | Supported by most modern CPUs and GPUs, executed in a single instruction cycle | Executed on specialized hardware like NVIDIA's Tensor Cores | Software-implemented but optimized for hardware capabilities (e.g., using SIMD instructions) |
| **Application** | Widely used in numerical computations and is a part of CPU instruction sets like FMA3 or FMA4 | Utilized in specialized domains, particularly deep learning on GPUs | Core function in BLAS, crucial for high-performance computing, scientific computing, and deep learning |

### Tensor core 和 Cuda core 差別
- tensor core和cuda core 都是運算單元，是硬體名詞，其主要的差異是算力和運算場景。
- 場景：cuda core是全能通吃型的浮點運算單元，tensor core專為深度學習矩陣運算設計。
- 算力：在高精確度矩陣運算上 tensor cores 大勝 cuda cores。

| 特性 | Tensor Core | CUDA Core |
| ---- | ---- | ---- |
| **出現背景** | AI快速發展，對矩陣乘法的算力需求不斷增大，有廠商提出TPU概念 | 科學計算迅速發展，為了使用GPU的高算力，科學家需要將科學計算任務適配成圖形影像任務 |
| **設計目的** | 強化矩陣運算能力（AI算力），融入CUDA生態 | 將高平行度的浮點運算能力提供給科學運算領域，加速科學運算，佔領科學計算市場 |
| **計算任務類型** | 矩陣乘法運算 | 浮點加、乘、乘加運算 |
| **計算精度** | 強調低精度: fp16/fp8/int8/int4/b1 | IEEE-754 標準的float精度 |
| **SM上的裝配數目** | 8 | 128 |
| **調度粒度/執行粒度** | warp-level/warp-level | warp-level/thread-level |
| **每GPU Cycle的計算速度** | multiply two 4 x 4 F16 matrices and add the multiplication product fp32 matrix per GPU cycle | 1 single precision multiply-andaccumulate operation per GPU cycle |
| **運算速度** | 125 Tflops/s | 15.7 Tflops/s |

## Lesson of Tensor Core
### Thread-Level Parallelism (TLP) for MMA Execution

- **TLP in Action**: Tensor Cores demonstrate Thread-Level Parallelism by dividing matrix operations across multiple threads within a warp. This form of parallelism can be leveraged in other contexts where tasks can be decomposed into smaller, independent sub-tasks.

### Special Functional Units for DP Calculation

- **Dedicated Hardware for Specific Tasks**: The specialized nature of Tensor Cores for double-precision (DP) and mixed-precision calculations shows the benefits of having dedicated hardware for specific types of computation. This can lead to both increased speed and efficiency.

### Data Reuse

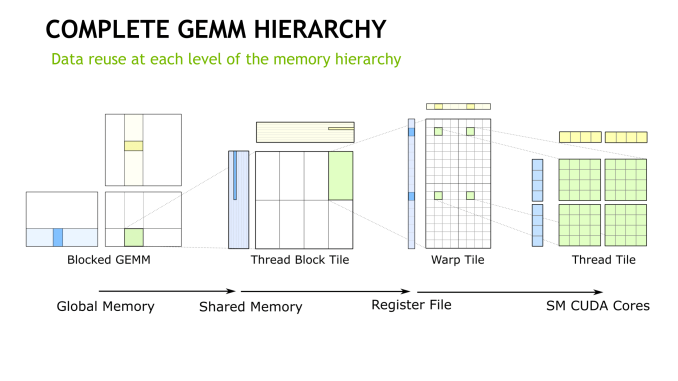
- **Optimizing Data Access**: By reusing data effectively (such as keeping a tile in shared/local memory for as long as possible), we can reduce the need for slow memory accesses. This principle of data locality and reuse is essential for optimizing performance in any system.

### ISA Support

- **Instruction Set Architecture (ISA) Extensions**: Tensor Cores require support from specialized ISA (like WMMA in CUDA) provided by the compiler. This demonstrates the importance of ISA extensions in unlocking new hardware capabilities and optimizing performance.

# Ref:

- Course slides: Accelerator Architectures for Machine Learning Lecture 8: Tensor Core, Tsung Tai Yeh

- Maohua Zhu, Tao Zhang, Zhenyu Gu, and Yuan Xie. 2019. Sparse Tensor Core: Algorithm and Hardware Co-Design for Vector-wise Sparse Neural Networks on Modern GPUs. In Proceedings of the 52nd Annual IEEE/ACM International Symposium on Microarchitecture (MICRO '52). Association for Computing Machinery, New York, NY, USA, 359–371. https://doi.org/10.1145/3352460.3358269

- Sun, W., Li, A., Geng, T., Stuijk, S., & Corporaal, H. (2022). Dissecting Tensor Cores via Microbenchmarks: Latency, Throughput and Numeric Behaviors. IEEE Transactions on Parallel and Distributed Systems, 34(1), 246-261.
- [Programming Tensor Cores in CUDA 9 | NVIDIA Technical Blog](https://developer.nvidia.com/blog/programming-tensor-cores-cuda-9/)