2017q3 Homework1 (ternary)

contributed by <louis222220>

Reviewed byvonchuang

• 在 Balanced Ternary 的壞處中列了一項："目前的電腦架構幾乎為Binary"，然此並非其壞處，只是結果
• "老實說目前雖然瀏覽過了這些文章，還是不了解 Balanced Ternary 解決了什麼問題"，可參考 The Balanced Ternary Machines of Soviet Russia 及 THE TECH BEHIND IOTA EXPLAINED
• 文中部分內容的中英文未以空白相隔
• "這樣就能實現Balanced Ternary 半加法器，進一步完成全加法器"，可對全加器詳述之

作業要求

• [ ]研讀 Balanced Ternary，並依據 課前測驗參考解答: Q1 的風格和探討方式，涵蓋以下:
  • 解釋 Balanced Ternary 原理;
  • Balanced Ternary 的設計要解決什麼類型的問題，需要詳述實際應用案例 (如 IOTA/Tangle)。提示：從算術表達的精準度和空間使用效率去探討;
  • 針對特定的領域 (如加密貨幣)，列出在 GitHub 裡頭可找到的應用案例，不僅列出程式碼，還要解說;
  • 在研究的過程中，應該會對既有工具進行修改或者重新開發 (不限程式語言)，也該一併指出，程式碼應該維護在 GitHub 上;
  • 建立新的 HackMD 頁面，並列於 作業區。撰寫數學式應該全部用 LaTeX 表示，不該用圖片
• [ ]在 GitHub 上 fork balanced-ternary，針對你的分析需求，進行必要的修改
  • [ ]提交修改前，務必確認詳讀 如何寫好 Git Commit Message

---

---

解釋 Balanced Ternary 原理

Ternary簡介

Ternary 三進位是以3為基數的進位數字系統，以0,1,2來表示每一位數，相較於 Binary 二進位以0,1來表示的數字系統。用 Ternary 來表示同一個數字，能比 Binary 使用更少的位數。
example:
10₁₀ = (1 * 10¹) + (0 * 10⁰) = 10₁₀ + 0
1010₂ = (1 * 2³) + (0 * 2²) + (1 * 2¹) + (0 * 2⁰) = 8₁₀ + 2₁₀
101₃ = (1* 3²) + (0 * 3¹) + (1 * 3⁰) = 9₁₀ + 1₁₀

Decimal	Binary	Ternary
0	0	0
1	1	1
2	10	02
10	1010	101

Balanced Ternary 簡介

• 每一個位元(trit)使用-1, 0, 1作為值，取代原本 Ternary 的0, 1, 2
• 可用-, 0, + 或 T, 0, 1 來表示

數字表示方式^[6]

將三進位數值表示成十進位數值算法為 ：

${\displaystyle \sum _{k=1}^i{a}_k\times 3^{k-1}+{\displaystyle \sum _{n=1}^j{a}_n\times 3^{-n}}}$
其中

$i$ 為三進位數值整數部分的trit，

$j$ 為三進位數值小數部分的trit

$a_k$ 及

$a_n$ 為

$T$、

$0$ 或

$1$

• 負數的轉換只要將 Balanced Ternary 中的每個trit做Bitwise NOT處理

• 整數
  e.g.

  $1T1T_{bal3}=1\times 3^3+(-1)\times 3^2+1\times 3^1+(-1)\times 3^0=27-9+3-1={20}_{dec}$
  e.g.
  $T1T{1}_{bal3}=(-1)\times 3^3+1\times 3^2+(-1)\times 3^1+1\times 3^0=-27+9-3+1=-{20}_{dec}$

• 分數(小數)
  e.g.

  ${\displaystyle \frac{1}{3}}=1\times 3^{-1}={0.1}_{bal3}$
  e.g.
  ${\displaystyle \frac{1}{2}}=0.{\bar{1}}_{bal3}$
  
  $\frac{1}{2}\times 3=1+\frac{1}{2}$
  
  $\frac{1}{2}\times 3=1+\frac{1}{2}$ (循環…)

Logic

定義

Kleene 從 Binary 的 true, false 延伸出 Ternary 的布林代數^[3,4,7]

truth value	ternary	balanced ternary
false	0	-
unknown	1	0
true	2	+

邏輯運算

• NOT

NOT	value
-	+
0	0
+	-

• • AND (相當於是MIN)

AND	-	0	+
-	-	-	-
0	-	0	0
+	-	0	+

• OR (相當於是MAX)

OR	-	0	+
-	-	0	+
0	0	0	+
+	+	+	+

• SUM
  相加

SUM	-	0	+
-	+	-	0
0	-	0	+
+	0	+	-

• Consensus

CONS	-	0	+
-	-	0	0
0	0	0	0
+	0	0	+

Balanced Ternary Operation

利用 Balanced Ternary 的邏輯運算

• 半加法器
  Input:
  $a_i$、
  $c_i$
  Output:
  $c_{i+1}$、
  $s_i$

真值表:

$a_i$	$c_i$	$c_{i+1}$	$s_i$
-	-	-	+
-	0	0	-
-	+	0	0
0	-	0	-
0	0	0	0
0	+	0	+
+	-	0	0
+	0	0	+
+	+	+	-

可分別整理成

$c_{i+1}$	-	0	+
-	-	0	0
0	0	0	0
+	0	0	+
$c_{i+1}$ = CONS( $a_i$, $c_i$)

$s_i$	-	0	+
-	+	-	0
0	-	0	+
+	0	+	-
$s_i$ = SUM( $a_i$, $c_i$)
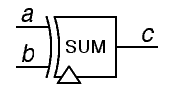
因此完整的半加法器邏輯圖表示為

電路

Balanced Ternary 加法器可以透過多個3-to-1 Multiplexer 來實現^[5]
如下圖，Selector 針腳的-1, 0, 1決定輸出哪一個輸入的電位

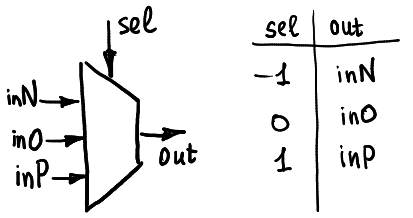
首先藉由 Mux，改變Input腳位的值，做出A+1及A-1, MIN(A,0), MAX(A,0)
舉例A+1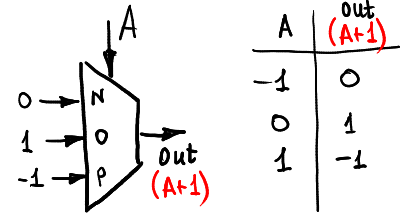

透過A-1, A, A+1，以B當作Selector腳位，就可以完成SUM(A,B)

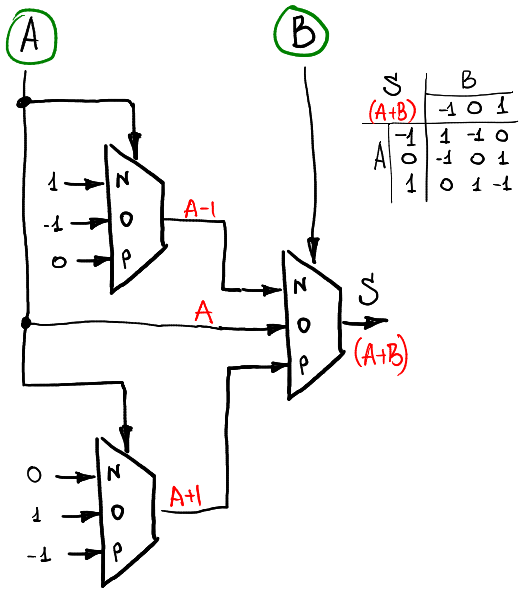
MIN(A,0), 0, MAX(A,0)則可以完成CONS(A,B)

這樣就能實現Balanced Ternary 半加法器，進一步完成全加法器

Balanced Ternary 好處與壞處

好處:

• 相比於 Binary 可以用較少的位數表示相同精度的值
• 處理速度較快 (e.g. ripple-carry adder能用更少的階層計算完)

壞處:

• Balanced Ternary 相較於 Binary 的電路設計更為複雜
• 目前的電腦架構幾乎為Binary

---

Balanced Ternary 的設計要解決什麼類型的問題

老實說目前雖然瀏覽過了這些文章，還是不了解 Balanced Ternary 解決了什麼問題，
利用 Ternary 可以在相同位數內儲存更大的數字，在資料或運算空間需求大的應用上會有用處，例如需要體積小低供耗的 IoT 設備上、金融系統的數字儲存，但應該還有其他因素，形成 Ternary 逐漸受到重視

---

測試 Balanced Ternary

balanced-ternary 程式的功能是將輸入的十進位數字轉換成 Balanced Ternary，並以圖形呈現

方形的4個面及4個角落，各自表示一個 trit，依順時針從正下方開始是最小的 trit，每個 trit 向外的分支表示+，向內表示-

┌───┐  
│   │ = 0
└───┘
┌───┐
┤   │ = 3^2 + 1 = 10
└─┬─┘
┌┬──┐
│   │ = -3^3 = -27
└───┘
├─┴─┤
┤   ├ = 3^7 + 3^6 + 3^5 + 3^4 + 3^3 + 3^2 + 3 + 1 = 3280
├─┬─┤
┌┬┬┬┐
├   ┤ = -3^7 - 3^6 - 3^5 - 3^4 - 3^3 - 3^2 - 3 - 1 = -3280
└┴┴┴┘

此圖形共能表示8 trit，因此能表示的最大數字範圍為:

$\pm {\displaystyle \frac{(3^8-1)}{2}}$ , -3280~3280
(在此程式中，若輸入超過最大或最小值，則分別以最大或最小值取代)

程式中共有 3 個階段

1. 將輸入的數字轉成 Ternary 的3補數表示
2. 從3補數轉換成 balanced ternary
   每一 trit 中
   
   $0_{3^{\prime }s}=0_{bal3}$
   
   $1_{3^{\prime }s}=1_{bal3}$
   
   $2_{3^{\prime }s}=1T_{bal3}$
   依照 trit 從小到大依序轉換
3. 根據每個 trit 的 1, 0, -1，在相對應的位置輸出向內或向外的分支

---

Reference

1. Wikipedia: Ternary numeral system
2. Wikipedia: Balanced ternary
3. Fast Ternary Addition
4. Standard Ternary Logic
5. Ternary computing: basics
6. poyushen HackMD 共筆
7. Wikipedia: Three-valued logic