# [2017q3 Homework1 (ternary)](https://hackmd.io/@jserv/Sym0UAk9Z?type=view0)
contributed by <`vonchuang`>
:::info
1. 已列出 IOTA 中以python 實作 ANY、full adder 以及 ripple-carry adder 的程式碼列表,但沒有 IRI 的部分
> 尚未尋得
2. 「效率更好的加法器應為 Carry Lookahead ,然其在 Balanced ternary 實作上結構複雜」 => 著手實驗了嗎?
> 待補[color=red]
3. 「在上方程式法第 21 行處可看出,IOTA 使用於 Transaction 的 Hash Function 為 Curl,是 IOTA團隊為了解決問題而建立的新 Hash Function」 => 描述正確嗎?
> 已改善
4. 光有程式列表,但沒有實際測試和評估,怎知道實際狀況?
> 待補[color=red]
:::
>為何近五天都沒進展?00
>[name=課程助教][color=red]
>>先去研究phonebook...
>>[name=vonchuang][color=blue]
>>
## 目錄
* 摘要簡介:Balanced Ternary
* 原理
* Radix Economy
* 十進位、二進位、三進位比較
* 加減運算
* bal3 to dec ( 數字系統轉換 )
* dec to bal3 ( 數字系統轉換 )
* Half Adder(電路實作)
* Full Adder(電路實作)
* 歷史
* 應用:IOTA
* IOTA 簡介
* Balanced Ternary 應用
* IOTA 架構
* Curl
* Kerl
* IRI
* 參考資料
## 摘要簡介:Balanced Ternary
Donald Knuth 在其名著 the art of computer programming中提及:
> "Perhaps the pretties number system of all is the balance ternary notation."
本篇欲探討 Balanced Ternary 的原理及表示、從數學上證明三進位的經濟ㄧ性,並研究如何以電路實作其半加器及全加器,最後嘗試從多篇參考資料及原始碼中找出 Balanced Ternary 如何應用在 IOTA 中,以及為什麼會選擇使用 Balanced Ternary。
## 原理
- [ ] **TODO:檢查、歷史待補、實作**
在二進位,我們用`0`與`1`表達 False 和 True。而在三進位,則用`0`、`1`、`2`表示 False、Unknown 和 True;平衡三進位(Balanced Ternary)則用`-1`、`0`、`1`表示,其又可簡寫為`T`、`0`、`1`。
由於平衡三進位有負數,因此不用額外的位元即可直接表達負數。
若要表達某數之相反數,則只需把`T`與`1`相互調換即可。
如 $24.8_{dec}=10T1.T11T_{bal3}$,則 $-24.8_{dec}=T01T.1TT1_{bal3}$
### Radix Economy
在二進位,每一個位數叫做一個`bit`,三進位下每一個位數叫做一個`trit`。
一個位數在基數為 b 的數字下能負載 $log_{2}b$ 個 bit。故在三進位,一個 trit 能負載大約 1.58 bits;十進位下的一個位數則能負載約莫 3.32 bits。然相對的,十進位的每個位數皆有十種不同可能的值,遠比二進位及三進位複雜。
而將以上兩種比較方式綜合考量,即為基需(Radix Economy)的概念。
簡單來說,基需係指在一個固定基數下,表示一個數所需的開銷。比如,若欲表示 1000 以下的數,在十進位制需 3 位數,在八進位制需 4 位數,在二進位制下則需 10 位數。
已知對於任意數 N,在基數 b 下表示數字 N 需要 $log_{b}N+1$ 位數。故基需的精確定義為:
$E(b,N)=b\times(log_{b}N+1)$
舉例來說,表示999時,十進位下的基需是 $10\cdot3=30$,八進位下的基需是 $8\cdot4=32$,二進位下的基需是 $2\cdot10=20$。
那麼,在何時基需為最小?
由 $E(b,N)=b\times(log_{b}N+1)\approx b\times log_{b}N=(b/ln(b))\times ln(N)$ 可知在 $b=e$ 時,基需為最小。
>The base $e$ is the most economical choice of radix β>1 (Hayes 2001), where the radix economy is measured as the product of the radix and the length of the string of symbols needed to express a given range of values.
而3是最接近 $e$ 的整數,故我們從數學上證明了三進位是最經濟的。

*圖片出處:[三生萬物](http://www.global-sci.org/mc/issues/5/no4/freepdf/79s.pdf)*
#### 參考資料:
* [三生萬物](http://www.global-sci.org/mc/issues/5/no4/freepdf/79s.pdf)
* [What is the most efficient numerical base system?](https://math.stackexchange.com/questions/446664/what-is-the-most-efficient-numerical-base-system)
* [Wikipedia:Non-integer representation](https://en.wikipedia.org/wiki/Non-integer_representation)
### 十進位、二進位、三進位比較
|十進位| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10|
| - | - | - | - | - | - | - | - | - | - | - |
|二進位| 1 | 10 | 11 | 100 | 101 | 110 | 111| 1000 | 1001 | 1010 |
|三進位| 1 | 2 | 10 | 11 | 12 | 20 | 21 | 22 | 100 | 101 |
|平衡三進位| 1 | 1T | 10 | 11 | 1TT | 1T0 | 1T1 | 10T | 100 | 101 |
### 加減運算
與十進位、二進位依樣,逐位做加減法即可。如:
$\ \qquad 1TT1TT.1TT1 \\ \underline{\ +\qquad\ \ 11T1.T\ \ \ \ \ \ }\\\qquad\ \ \ 1T0T10.0TT1\\\underline{\ +\qquad\ \ 1T\ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\qquad\ \ \ 1T1110.0TT1\\\underline{\ +\qquad\ \ T\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }\\\ \ \ \qquad 1T0110.0TT1$
### bal3 to dec ( 數字系統轉換 )
各位的數字和位權相乘然後疊加起來,即為該數的數值。
範例:
$\begin{split}
1TT1.TT&=1\cdot3^3+(-1)\cdot3^2+(-1)\cdot3^1+1\cdot3^0+(-1)\cdot3^{-1}+(-1)\cdot3^{-2} \\
&=15\dfrac{5}{9}
\end{split}$
### dec to bal3 ( 數字系統轉換 )
可由以下公式完成轉換:
$(a_{n}a_{n-1}...a_{1}a_{0}.c_{1}c_{2}c_{3}...)_{b}
=\displaystyle\sum_{k=0}^na_{k}b^k+\displaystyle\sum_{k=1}^{\infty}c_{k}b^{-k}$
其中$a_{n}a_{n-1}...a_{1}a_{0}.c_{1}c_{2}c_{3}...$為原數字系統之表示。
b 為原基數,如若原數字系統為十進位,b 則為10。
$a_{k}$和$c_{k}$分別為整數和小數部分之數字。
範例:
$\begin{split}
24.8_{dec}
&=1T\cdot(101)^1+11\cdot(101)^0+10T\cdot(101)^T \\
&=1T1T+11+10T/101 \\
&=10T1.\overline{T11T}_{bal3}
\end{split}$
#### 參考資料
* [Wikipedia:Balanced ternary](https://en.wikipedia.org/wiki/Balanced_ternary)
### Half Adder(電路實作)
* 若欲更了解 Balanced Ternary 的原理及基礎運算操作,可回到最原本的電路上。
* 以下以電路實作出 Balanced Ternary 的半加器,首先須先列出其 Truth Table:
| $\ \ inputs\\a_{i}\qquad c_{i}$ | $\ outputs\\c_{i+1}\ \ \ \ \ s_{i}$|
|:------:|:------:|
| $-\qquad -$ | $-\qquad +$ |
| $-\qquad 0$ | $0\qquad -$ |
| $-\qquad +$ | $0\qquad 0$ |
| $0\qquad -$ | $0\qquad -$ |
| $0\qquad 0$ | $0\qquad 0$ |
| $0\qquad +$ | $0\qquad +$ |
| $+\qquad -$ | $0\qquad 0$ |
| $+\qquad 0$ | $0\qquad +$ |
| $+\qquad +$ | $+\qquad -$ |
| $\\ c_{i+1}$ | $\ \ \ \ \ c_{i}\\-\ 0\ +$ |
|:------:|:------:|
| $\ \ \ \ -\\a_{i}\ \ 0 \\ \ \ \ \ \ +$ | $-\ \ 0\ \ 0\\ 0\ \ \ 0\ \ 0\\0\ \ \ 0\ \ +$ |
| $\\ s_{i}$ | $\ \ \ \ \ c_{i}\\-\ 0\ +$ |
|:------:|:------:|
| $\ \ \ \ -\\a_{i}\ \ 0 \\ \ \ \ \ \ +$ | $+\ \ -\ \ 0\\ -\ \ \ 0\ \ +\\0\ \ \ +\ \ -$ |
* 為了實現加法器,在此先設計出一 ternary multiplexer,共五個 pin 腳,依據 sel之數值(`-1`、`0`、`1`)選擇輸出 out 之值(`inN`、`inO`、`inP`)
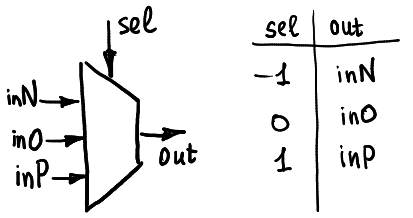
*圖片出處:[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)*
* 而此 ternary multiplexer,可依需求輸入不同的`inN`、`inO`、`inP`,使作出所需效果。在此,為了實做出加法器,我們分別做出計算`A+1`、`A-1`、`min(A,0)`、`max(A,0)`之 ternary multiplexer:

*圖片出處:[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)*
* 有了以上的 multiplexers,現在可以分別實作出半加器的 $S$ 和 $C_{out}$。

*圖片出處:[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)*
* 最後,將以上二者結合起來,即做出 Balanced Ternary 的半加器。

*圖片出處:[github:ternary-logisim](https://github.com/ternary-info/ternary-logisim/blob/master/screenshots/ternary_half_adder.png)*
* 其中,以上之電路有又可用更為簡單的方式表示。$S$ 和 $C_{out}$可分別記為:

*圖片出處:[Standard Ternary Logic](http://homepage.divms.uiowa.edu/~jones/ternary/logic.shtml#sum)*
* 在此列出 IOTA 的 open source code 中以 python 實作 SUM 和 CONS 的部分:
```python=
function sum( a, b ) {
var s = a + b;
switch( s ) {
case 2: return -1;
case -2: return 1;
default: return s;
}
}
function cons( a, b ) {
if( a === b ) {
return a;
}
return 0;
}
```
* 故 Balanced Ternary 的半加器可以以下之圖示表示:

*圖片出處:[Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml#halfbalanced)*
### Full Adder(電路實作)
* 欲做出 Balanced Ternary 的全加器,一樣是先列出 True Table:

*圖片出處:[Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml#fullbalanced)*
* 當 $C_{in}=0$ 時,全加器即與半加器無異,故可知全加器可由半加器組成。
* 先分別實作出全加器的 $S$ 和 $C_{out}$(以下圖之綠色部分即為半加器):

*圖片出處:[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)*
* 最後,將二者和一,即為 Balanced Ternary 全加器。

*圖片出處:[github:ternary-logisim](https://github.com/ternary-info/ternary-logisim/blob/master/screenshots/ternary_full_adder.png)*
* Balanced Ternary 全加器的簡易圖示為:

*圖片出處:[Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml#fullbalanced)*
其中的 ANY 為:

*圖片出處:[Standard Ternary Logic](http://homepage.divms.uiowa.edu/~jones/ternary/logic.shtml#sum)*
* 在此列出 IOTA 的 open source code 中以python 實作 ANY、full adder 以及 ripple-carry adder 的部分:
```python=
function any( a, b ) {
var s = a + b;
if ( s > 0 ) {
return 1;
} else if ( s < 0 ) {
return -1;
}
return 0;
}
function full_add( a, b, c ) {
var s_a = sum( a, b );
var c_a = cons( a, b );
var c_b = cons( s_a, c );
var c_out = any( c_a, c_b );
var s_out = sum( s_a, c );
return [ s_out, c_out ];
}
function add( a, b ) {
var out = new Array( Math.max( a.length, b.length ) );
var carry = 0;
var a_i, b_i;
for( var i = 0; i < out.length; i++ ) {
a_i = i < a.length ? a[ i ] : 0;
b_i = i < b.length ? b[ i ] : 0;
var f_a = full_add( a_i, b_i, carry );
out[ i ] = f_a[ 0 ];
carry = f_a[ 1 ];
}
return out;
}
```
* 在上述全加器之 True Table 中,共有27種可能,在經過優化之後,可以一定程度上的減少,但在效率上仍舊不夠好。因以上之實作皆為 ripple-carry adder,一個 trit 的 balanced adder 分別需要 10 minterms 和 18 minterms 計算 $C_{out}$ 和 $S$,比起 unsigned 或 3's complement adder 多出大約 50% 的複雜度。故若以 ripple-carry adder 實作加法器,並以加法的複雜度為考量,balanced ternary 並非最佳選擇。
* 效率更好的加法器應為 Carry Lookahead ,然其在 Balanced ternary 實作上結構複雜,在此不詳述。更詳細的說明可參考 [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml#lookahead)
#### 參考資料
* [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)
* [github:ternary-logisim](https://github.com/ternary-info/ternary-logisim/)
* [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)
* [Standard Ternary Logic](http://homepage.divms.uiowa.edu/~jones/ternary/logic.shtml#sum)
* [github:iota.crypto.js/lib/crypto/helpers/adder.js](https://github.com/iotaledger/iota.crypto.js/blob/master/lib/crypto/helpers/adder.js)
### 歷史
- [ ] **TODO**:待補
- [ ] **TODO**:參考nienzu評論:這裡打出來的參考資料在[這篇 Reddit](https://www.reddit.com/r/programming/comments/5e3f4n/the_balanced_ternary_machines_of_soviet_russia/) 的文章中的留言有人提到 Setun is a victim of complicated politics... ,然後在這篇俄文的文章提到當時發展 Setun 的歷史背景(感謝 google 翻譯),另外則是俄羅斯的電腦博物館的文獻,兩者對於理解當時的情況很有幫助 [Development of ternary computers at Moscow State University](http://www.computer-museum.ru/english/setun.htm),最後[Ternary Computers: The Setun and the Setun 70](https://hal.inria.fr/hal-01568401/document)這篇整理的很完整
## 應用:IOTA
### IOTA 簡介
IOTA(一種用於物聯網行業的無區塊鍊加密貨幣系統),其中的 IOT 代表 Internet of Things,最後的 A 則有幾個意思:
* Applications,物聯網的應用
* Apocalyse,物聯網的啟事
* Asset,物連往就是財富
* 字母A,代表最小可能的事情,暗含著 IOTA 的輕量級、零交易費、微交易等特性
過去,比特幣的興起和成功正名了區塊練的價值,但這種技術也有許多缺點,其中之一即是無法進行小額支付,而小額支付在迅速發展的物聯往行業中的重要性不斷增加。在 [IOTA_Whitepaper](http://www.tangleblog.com/wp-content/uploads/2016/11/IOTA_Whitepaper.pdf) 中提及:
>Specifically, in the currently available systems one must pay a fee for making a transaction; so, transferring a very small amount just makes no sense since one would have also to pay the fee which is many times larger.
### Balanced Ternary
IOTA 是基於 Balanced Ternary(base 3)而非 Binary(base 2)。可在 [iota.lib.py/iota/types.py](https://github.com/iotaledger/iota.lib.py/blob/master/iota/types.py) 找到其以 python 實作 trits 和 int 相互轉換的程式碼:
```python=
def trits_from_int(n, pad=None):
# type: (int, Optional[int]) -> List[int]
"""
Returns a trit representation of an integer value.
:param n:
Integer value to convert.
:param pad:
Ensure the result has at least this many trits.
References:
- https://dev.to/buntine/the-balanced-ternary-machines-of-soviet-russia
- https://en.wikipedia.org/wiki/Balanced_ternary
- https://rosettacode.org/wiki/Balanced_ternary#Python
"""
if n == 0:
trits = []
else:
quotient, remainder = divmod(n, 3)
if remainder == 2:
# Lend 1 to the next place so we can make this trit negative.
quotient += 1
remainder = -1
trits = [remainder] + trits_from_int(quotient)
if pad:
trits += [0] * max(0, pad - len(trits))
return trits
def int_from_trits(trits):
# type: (Iterable[int]) -> int
"""
Converts a sequence of trits into an integer value.
"""
# Normally we'd have to wrap ``enumerate`` inside ``reversed``, but
# balanced ternary puts least significant digits first.
return sum(base * (3 ** power) for power, base in enumerate(trits))
```
在 IRI(IOTA Reference Implementation)中,則可在 [Converter.java](https://github.com/iotaledger/iri/blob/dev/src/main/java/com/iota/iri/utils/Converter.java) 中找到 trits 和 trytes 的設定。
此外,IOTA 亦使用 Ternary JINN-Processors

IOTA 的創辦人之一 David Sønstebø:
> JINN is a custom made Polymorphic Processing Unit which utilizes asynchronous circuits and trinary logic gates, a component of this is the ‘Curl Hasher’ (essentially a tiny ASIC), this ‘Curl Hasher’ component will be made open source so that any chip manufacturer can add it to their chips trivially. We’re talking a completely negligible amount of logic gates here, so zero extra cost, size trade off or implementation issues
#### But Why Ternary?
* 在 [The Balanced Ternary Machines of Soviet Russia](https://dev.to/buntine/the-balanced-ternary-machines-of-soviet-russia) 提及,因 Balanced Ternary 有正有負,因此不用額外的位元即可直接表達負數。也因此在做減法時,只需將減數正負反轉並將被減數及減數相加即可,可提升空間使用率(觀察上方所列程式碼的第 10 行注釋可知,IOTA 團隊亦是參考這篇文章)。
* 另外,在 [THE TECH BEHIND IOTA EXPLAINED](http://www.tangleblog.com/2017/01/25/the-tech-behind-iota-explained/) 中提及另一個選擇 Balanced Ternary的原因:
> These 3 states perform transaction very balanced, which is quite helpful to build a self-organizing and self-sustaining network like the tangle.
* 參考資料:
* [The Balanced Ternary Machines of Soviet Russia](https://dev.to/buntine/the-balanced-ternary-machines-of-soviet-russia)
* [THE TECH BEHIND IOTA EXPLAINED](http://www.tangleblog.com/2017/01/25/the-tech-behind-iota-explained/)
### IOTA 架構
IOTA 的中心架構為 [DAG](https://en.wikipedia.org/wiki/Directed_acyclic_graph)(Directed Acyclic Grapgh),稱之為 Tangle。其一個新的交易產生,必須有以下步驟:
* 選擇兩個交易驗證(這兩比交易可能會一樣)
* 檢查這兩筆交易有無衝突,且有無驗證到衝突的交易
* 要讓一筆交易合法(valid),發起交易者必須解出一道加密的問題(耗費計算力),與比特幣挖礦相似
> it needs to find a **nonce** such that the hash of that nonce together with some data from the approved transactions has a particular form, for instance, has at least some fixed number of zeros in front.
根據 IOTA open source code 的 [git commit](https://github.com/iotaledger/iota.lib.py/commit/f098b1a5e0bab34e637853ed01e2861a9d6d51fb),在 IOTA Python API Library 中,nonce 是在 2017/9/25 新增的 type,宣告在 [iota.lib.py/iota/transaction/types.py](https://github.com/iotaledger/iota.lib.py/blob/master/iota/transaction/types.py) 中:
```python=
class Nonce(TryteString):
"""
A TryteString that acts as a transaction nonce.
"""
LEN = 27
def __init__(self, trytes):
# type: (TrytesCompatible) -> None
super(Nonce, self).__init__(trytes, pad=self.LEN)
if len(self._trytes) > self.LEN:
raise with_context(
exc = ValueError('{cls} values must be {len} trytes long.'.format(
cls = type(self).__name__,
len = self.LEN
)),
context = {
'trytes': trytes,
},
)
```
在 [iota.lib.py/iota/transaction/base.py](https://github.com/iotaledger/iota.lib.py/blob/master/iota/transaction/base.py) 的 class Transaction 中即包含 nonce(下方程式碼的第 43 行、第48~51行處):
```python=
class Transaction(JsonSerializable):
"""
A transaction that has been attached to the Tangle.
"""
@classmethod
def from_tryte_string(cls, trytes, hash_=None):
# type: (TrytesCompatible, Optional[TransactionHash]) -> Transaction
"""
Creates a Transaction object from a sequence of trytes.
:param trytes:
Raw trytes. Should be exactly 2673 trytes long.
:param hash_:
The transaction hash, if available.
If not provided, it will be computed from the transaction trytes.
"""
tryte_string = TransactionTrytes(trytes)
if not hash_:
hash_trits = [0] * HASH_LENGTH # type: MutableSequence[int]
sponge = Curl()
sponge.absorb(tryte_string.as_trits())
sponge.squeeze(hash_trits)
hash_ = TransactionHash.from_trits(hash_trits)
return cls(
hash_ = hash_,
signature_message_fragment = Fragment(tryte_string[0:2187]),
address = Address(tryte_string[2187:2268]),
value = int_from_trits(tryte_string[2268:2295].as_trits()),
legacy_tag = Tag(tryte_string[2295:2322]),
timestamp = int_from_trits(tryte_string[2322:2331].as_trits()),
current_index = int_from_trits(tryte_string[2331:2340].as_trits()),
last_index = int_from_trits(tryte_string[2340:2349].as_trits()),
bundle_hash = BundleHash(tryte_string[2349:2430]),
trunk_transaction_hash = TransactionHash(tryte_string[2430:2511]),
branch_transaction_hash = TransactionHash(tryte_string[2511:2592]),
tag = Tag(tryte_string[2592:2619]),
attachment_timestamp = int_from_trits(tryte_string[2619:2628].as_trits()),
attachment_timestamp_lower_bound = int_from_trits(tryte_string[2628:2637].as_trits()),
attachment_timestamp_upper_bound = int_from_trits(tryte_string[2637:2646].as_trits()),
nonce = Nonce(tryte_string[2646:2673]),
)
...
self.nonce = nonce # type: Optional[Nonce]
"""
Unique value used to increase security of the transaction hash.
"""
```
* 在 [iota/iri/hash/](https://github.com/iotaledger/iri/tree/dev/src/main/java/com/iota/iri/hash) 可看到,IOTA 主要使用的 Hash Function 為 **Curl** 和 **Kerl**,是由 IOTA 團隊基於 [Keccak](https://keccak.team/index.html) 建立新 Hash Function,以下分別介紹之。
### Curl
在 [The Transparency Compendium](https://blog.iota.org/the-transparency-compendium-26aa5bb8e260),IOTA 團隊如此介紹 Curl:
> As IOTA was the first distributed ledger project that took the inevitable threat of scalable quantum computers seriously, we had to move away from standard elliptic curve cryptography. [A few months later NSA validated our concerns by announcing official concern over the ‘quantum threat’](https://www.schneier.com/blog/archives/2015/08/nsa_plans_for_a.html). Since then there has been numerous quantum leaps in quantum computing, further validating this engineering decision we made. Beyond this concern we also had to follow a path that is optimized for the future landscape of Internet of Things. Curl is a new kind of hash function optimized precisely for these two things, it is based on well-studied sponge construction invented by the Keccak creators (SHA-3) and strictly conforms to all requirements [described in their official paper](https://keccak.team/files/CSF-0.1.pdf). Though Curl has gone through reviews, it is naturally not as explored as older ones yet. Curl, like the rest of IOTA, is continuously being audited by more and more cryptographers and security experts. IOTA currently uses Keccak (SHA-3) for signing as a security precaution.
目前 IOTA 將 Curl 用於 transaction ID grnrration 和 proof of work 上。同樣在 [iota.lib.py/iota/transaction/base.py](https://github.com/iotaledger/iota.lib.py/blob/master/iota/transaction/base.py) 中皆可找到(在上方程式碼第 28 行、第 36~38 行及以下):
```python=
self.hash = hash_ # type: Optional[TransactionHash]
"""
Transaction ID, generated by taking a hash of the transaction
trits.
"""
self.bundle_hash = bundle_hash # type: Optional[BundleHash]
"""
Bundle hash, generated by taking a hash of metadata from all the
transactions in the bundle.
"""
self.trunk_transaction_hash = trunk_transaction_hash # type: Optional[TransactionHash]
"""
In order to add a transaction to the Tangle, you must perform PoW
to "approve" two existing transactions, called the "trunk" and
"branch" transactions.
The trunk transaction is generally used to link transactions within
a bundle.
"""
self.branch_transaction_hash = branch_transaction_hash # type: Optional[TransactionHash]
"""
In order to add a transaction to the Tangle, you must perform PoW
to "approve" two existing transactions, called the "trunk" and
"branch" transactions.
The branch transaction generally has no significance.
"""
```
#### Curl 原理及實作
在 [ccurl/src/lib/curl.c](https://github.com/iotaledger/ccurl/blob/master/src/lib/curl.c) 中可找到以 C 實作 Curl 的程式碼:
* 在程式開頭先定義 Balanced Ternary 的 True table 和 Hash table
```c=
#define __TRUTH_TABLE 1, 0, -1, 2, 1, -1, 0, 2, -1, 1, 0
#define __INDEX_TABLE \
0, 364, 728, 363, 727, 362, 726, 361, 725, 360, 724, 359, 723, 358, 722,\
357, 721, 356, 720, 355, 719, 354, 718, 353, 717, 352, 716, 351, 715, 350,\
714, 349, 713, 348, 712, 347, 711, 346, 710, 345, 709, 344, 708, 343, 707,\
342, 706, 341, 705, 340, 704, 339, 703, 338, 702, 337, 701, 336, 700, 335,\
699, 334, 698, 333, 697, 332, 696, 331, 695, 330, 694, 329, 693, 328, 692,\
327, 691, 326, 690, 325, 689, 324, 688, 323, 687, 322, 686, 321, 685, 320,\
684, 319, 683, 318, 682, 317, 681, 316, 680, 315, 679, 314, 678, 313, 677,\
312, 676, 311, 675, 310, 674, 309, 673, 308, 672, 307, 671, 306, 670, 305,\
669, 304, 668, 303, 667, 302, 666, 301, 665, 300, 664, 299, 663, 298, 662,\
297, 661, 296, 660, 295, 659, 294, 658, 293, 657, 292, 656, 291, 655, 290,\
654, 289, 653, 288, 652, 287, 651, 286, 650, 285, 649, 284, 648, 283, 647,\
282, 646, 281, 645, 280, 644, 279, 643, 278, 642, 277, 641, 276, 640, 275,\
639, 274, 638, 273, 637, 272, 636, 271, 635, 270, 634, 269, 633, 268, 632,\
267, 631, 266, 630, 265, 629, 264, 628, 263, 627, 262, 626, 261, 625, 260,\
624, 259, 623, 258, 622, 257, 621, 256, 620, 255, 619, 254, 618, 253, 617,\
252, 616, 251, 615, 250, 614, 249, 613, 248, 612, 247, 611, 246, 610, 245,\
609, 244, 608, 243, 607, 242, 606, 241, 605, 240, 604, 239, 603, 238, 602,\
237, 601, 236, 600, 235, 599, 234, 598, 233, 597, 232, 596, 231, 595, 230,\
594, 229, 593, 228, 592, 227, 591, 226, 590, 225, 589, 224, 588, 223, 587,\
222, 586, 221, 585, 220, 584, 219, 583, 218, 582, 217, 581, 216, 580, 215,\
579, 214, 578, 213, 577, 212, 576, 211, 575, 210, 574, 209, 573, 208, 572,\
207, 571, 206, 570, 205, 569, 204, 568, 203, 567, 202, 566, 201, 565, 200,\
564, 199, 563, 198, 562, 197, 561, 196, 560, 195, 559, 194, 558, 193, 557,\
192, 556, 191, 555, 190, 554, 189, 553, 188, 552, 187, 551, 186, 550, 185,\
549, 184, 548, 183, 547, 182, 546, 181, 545, 180, 544, 179, 543, 178, 542,\
177, 541, 176, 540, 175, 539, 174, 538, 173, 537, 172, 536, 171, 535, 170,\
534, 169, 533, 168, 532, 167, 531, 166, 530, 165, 529, 164, 528, 163, 527,\
162, 526, 161, 525, 160, 524, 159, 523, 158, 522, 157, 521, 156, 520, 155,\
519, 154, 518, 153, 517, 152, 516, 151, 515, 150, 514, 149, 513, 148, 512,\
147, 511, 146, 510, 145, 509, 144, 508, 143, 507, 142, 506, 141, 505, 140,\
504, 139, 503, 138, 502, 137, 501, 136, 500, 135, 499, 134, 498, 133, 497,\
132, 496, 131, 495, 130, 494, 129, 493, 128, 492, 127, 491, 126, 490, 125,\
489, 124, 488, 123, 487, 122, 486, 121, 485, 120, 484, 119, 483, 118, 482,\
117, 481, 116, 480, 115, 479, 114, 478, 113, 477, 112, 476, 111, 475, 110,\
474, 109, 473, 108, 472, 107, 471, 106, 470, 105, 469, 104, 468, 103, 467,\
102, 466, 101, 465, 100, 464, 99, 463, 98, 462, 97, 461, 96, 460, 95,\
459, 94, 458, 93, 457, 92, 456, 91, 455, 90, 454, 89, 453, 88, 452,\
87, 451, 86, 450, 85, 449, 84, 448, 83, 447, 82, 446, 81, 445, 80,\
444, 79, 443, 78, 442, 77, 441, 76, 440, 75, 439, 74, 438, 73, 437,\
72, 436, 71, 435, 70, 434, 69, 433, 68, 432, 67, 431, 66, 430, 65,\
429, 64, 428, 63, 427, 62, 426, 61, 425, 60, 424, 59, 423, 58, 422,\
57, 421, 56, 420, 55, 419, 54, 418, 53, 417, 52, 416, 51, 415, 50,\
414, 49, 413, 48, 412, 47, 411, 46, 410, 45, 409, 44, 408, 43, 407,\
42, 406, 41, 405, 40, 404, 39, 403, 38, 402, 37, 401, 36, 400, 35,\
399, 34, 398, 33, 397, 32, 396, 31, 395, 30, 394, 29, 393, 28, 392,\
27, 391, 26, 390, 25, 389, 24, 388, 23, 387, 22, 386, 21, 385, 20,\
384, 19, 383, 18, 382, 17, 381, 16, 380, 15, 379, 14, 378, 13, 377,\
12, 376, 11, 375, 10, 374, 9, 373, 8, 372, 7, 371, 6, 370, 5,\
369, 4, 368, 3, 367, 2, 366, 1, 365, 0
static const size_t TRUTH_TABLE[11] = {__TRUTH_TABLE};
static const size_t INDEX[STATE_LENGTH+1] = {__INDEX_TABLE};
```
* Curl 如上所述,是基於 [Sponge function](https://en.wikipedia.org/wiki/Sponge_function) ,故與結構與其相似,主要分為兩部份:absorb(吸收)和squeeze(擠出)
* absorb 的程式碼如下:
```c=
void transform(curl_t* ctx);
void absorb(curl_t* ctx, char* const trits, int length) {
int offset = 0;
do {
memcpy(ctx->state, trits + offset,
(length < HASH_LENGTH ? length : HASH_LENGTH) * sizeof(char));
transform(ctx);
offset += HASH_LENGTH;
} while ((length -= HASH_LENGTH) > 0);
}
void transform(curl_t* ctx) {
int round, stateIndex;
char scratchpad[STATE_LENGTH];
for (round = 0; round < NUMBER_OF_ROUNDS; round++) {
memcpy(scratchpad, ctx->state, STATE_LENGTH * sizeof(char));
for (stateIndex = 0; stateIndex < STATE_LENGTH; stateIndex++) {
ctx->state[stateIndex] = TRUTH_TABLE[scratchpad[INDEX[stateIndex]] +
(scratchpad[INDEX[stateIndex+1]]<<2) +5 ];
}
}
}
```
一開始先將 offset 設為 0 後,將輸入(trits)和 offset 相加並複製前段一定長度到 type 為 curl_t 的 ctx 中(其中 curl_t 的 定義可在 [ccurl/src/lib/curl.h](https://github.com/iotaledger/ccurl/blob/master/src/lib/curl.h) 中找到)。
而後將 ctx 傳入填充函式(即transform)進行 Hash 處理。若填充後輸入還有剩餘,則進行下一區段的填充,直到所有輸入都用完為止(在海棉的譬喻裡面,被函式「吸收」了)。
* 而 squeeze 的程式碼如下:
```c=
void squeeze(curl_t* ctx, char* trits, int length) {
int offset = 0;
do {
memcpy(&(trits[offset]), ctx->state,
(length < HASH_LENGTH ? length : HASH_LENGTH) * sizeof(char));
transform(ctx);
offset += HASH_LENGTH;
} while ((length -= HASH_LENGTH) > 0);
}
```
先將 ctx 前一定長度的位元複製到 trits 中,並一樣將 ctx 傳到 transform 中進行 Hash 轉換,此時 trits 會隨著 ctx 一起進行轉換,重複此步驟直到滿足輸出所需要的長度為止(「擠出」內容)。
* 可在 [iota.lib.py/iota/crypto/pycurl.py](https://github.com/iotaledger/iota.lib.py/blob/master/iota/crypto/pycurl.py) 及 [iota.crypto.js/lib/crypto/curl/curl.js](https://github.com/iotaledger/iota.crypto.js/blob/master/lib/crypto/curl/curl.js) 中分別找到以 python 和 js 的程式碼(在此不詳述),但其實作方式與 C 不大相同,程式開發者在 python 檔案中的解釋是:
> This code looks significantly different from the C implementation because it has been optimized to limit the number of list item lookups (these are relatively slow in Python).
### Kerl
事實上,在 2017 年 8 月前,IOTA 亦將 Curl 使用在 Signature message hashing 中,但在 2017 年 7 月 14 日,有一團隊告知 IOTA 已找出有效的攻擊方式。
> 該團隊成員有: Ethan Heilman (Boston University, Paragon Foundation, Commonwealth Crypto), Neha Narula (MIT Media Lab), Thaddeus Dryja (MIT Media Lab, Lightning Network Dev), Madars Virza (MIT Media Lab, Zcash)
他們宣稱:
> We have developed practical attacks on IOTA’s cryptographic hash function Curl, allowing us to quickly generate short colliding messages. These collisions work even for messages of the same length. Exploiting these weaknesses in Curl, we break the EU-CMA security of the IOTA signature scheme. Finally we show that in a chosen message setting we can forge signatures of valid spending transactions (called bundles in IOTA).
而後兩方經過約半個月的討論,IOTA 在 2017 年 8 月 8 日將此部份的 Hash function 改為另一個由他們創立的,稱為 Kerl 的 Hash function(詳細改動部份可參考[Merged Kerl Implementation](https://github.com/iotaledger/iri/commit/539e413352a77b1db2042f46887e41d558f575e5) 這份 git commit),並在官方網站發表 [Upgrades & Updates](https://blog.iota.org/upgrades-updates-d12145e381eb) 的聲明。在 2017 年 9 月 8 日的[Curl disclosure, beyond the headline](https://blog.iota.org/curl-disclosure-beyond-the-headline-1814048d08ef) 中亦有提及此事:
> As part of an on-going conversation between the IOTA Team and security researchers from Boston University and MIT DCI, the teams published their report on a vulnerability in Curl today. On August 8th, the IOTA Team implemented a safety precaution by switching Curl with Keccak-384 (wrapped as “Kerl”, as a tongue-in-cheek homage to what it was replacing).
文中所提及的 report 在此:[IOTA Vulnerability Report: Cryptanalysis of the Curl Hash Function Enabling Practical Signature Forgery Attacks on the IOTA Cryptocurrency](https://github.com/mit-dci/tangled-curl/blob/master/vuln-iota.md)
其中有說明雙方討論的時間線,以及該團隊是以何種方式攻擊,並在 IOTA 完成 Upgrades & Updates 後在 [github](https://github.com/mit-dci/tangled-curl) 釋出原始碼(在此不詳述)。
* IOTA 並在 2017 年 8 月 22 日及 23 日將 [iota.lib.py](https://github.com/iotaledger/iota.lib.py) 中的部份 Hash 改 Curl 成 Kerl,更改部份可參考 [Key/Addy gen now uses kerl.](https://github.com/iotaledger/iota.lib.py/commit/d6b1437d8757c163f7ef976e3fde8f86a9964f13) 及 [s/Curl/Kerl/g](https://github.com/iotaledger/iota.lib.py/commit/f1aee1b2c6081fe31ae654b5e7b2f9c20b038407) 這兩份 git commit。
* 從這兩份 git commit 中可以看出,Kerl 主要是實作在 address 及 signing 的部份(~~以及,IOTA 的工程師之一 [todofixthis](https://github.com/todofixthis) 似乎沒有遵守 [How to Write a Git Commit Message](https://chris.beams.io/posts/git-commit/) 關於 git commit 的第四點建議,時常在 commit 的標題句末加了句號...->[證據](https://github.com/iotaledger/iota.lib.py/commits?author=todofixthis)~~)
* 在 [iotaledger/kerl](https://github.com/iotaledger/kerl) 中有以多種程式語言實作 Kerl 的程式碼。因為都是基於 Sponge function,故 Kerl 亦主要是由 absorb 和 squeeze 兩種 function 組成,但在 function 內部 Kerl 稍較複雜,以下列出以 python 3 實作的 absort 和 squeeze:
```python=
def absorb(self, trits, offset=0, length=None):
if length == None:
length = len(trits)
if length % 243 != 0:
raise Exception("Illegal length")
while offset < length:
stop = min(offset + TRIT_HASH_LENGTH, length)
# If we're copying over a full chunk, zero last trit
if stop - offset == TRIT_HASH_LENGTH:
trits[stop - 1] = 0
signed_nums = conv.convertToBytes(trits[offset:stop])
# Convert signed bytes into their equivalent unsigned representation
# In order to use Python's built-in bytes type
unsigned_bytes = bytes([conv.convert_sign(b) for b in signed_nums])
self.k.update(unsigned_bytes)
offset += TRIT_HASH_LENGTH
def squeeze(self, trits, offset=0, length=None):
if length == None:
length = TRIT_HASH_LENGTH
if length % 243 != 0:
raise Exception("Illegal length")
while offset < length:
unsigned_hash = self.k.digest()
signed_hash = [conv.convert_sign(b) for b in unsigned_hash]
trits_from_hash = conv.convertToTrits(signed_hash)
trits_from_hash[TRIT_HASH_LENGTH - 1] = 0
stop = TRIT_HASH_LENGTH
if length < TRIT_HASH_LENGTH:
stop = length
trits[offset:stop] = trits_from_hash[0:stop]
flipped_bytes = bytes([conv.convert_sign(~b) for b in unsigned_hash])
# Reset internal state before feeding back in
self.__init__()
self.k.update(flipped_bytes)
offset += TRIT_HASH_LENGTH
```
### IRI
在 IRI(IOTA Reference Implementation) 中,則是先宣告 interface Sponge 在 [Sponge.java](https://github.com/iotaledger/iri/blob/dev/src/main/java/com/iota/iri/hash/Sponge.java) 中
```java=
public interface Sponge {
void absorb(final int[] trits, int offset, int length);
void squeeze(final int[] trits, int offset, int length);
void reset();
}
```
Curl 和 Kerl 再分別繼承它,並 override absorb, squeeze 和 reset。
其原理與上述相似,故此處便不再墜述。
* [Curl.java](https://github.com/iotaledger/iri/blob/dev/src/main/java/com/iota/iri/hash/Curl.java)
```java=
public class Curl implements Sponge {
public static final int HASH_LENGTH = 243;
public static final int NUMBER_OF_ROUNDSP81 = 81;
public static final int NUMBER_OF_ROUNDSP27 = 27;
private final int numberOfRounds;
private static final int STATE_LENGTH = 3 * HASH_LENGTH;
private static final int HALF_LENGTH = 364;
private static final int[] TRUTH_TABLE = {1, 0, -1, 2, 1, -1, 0, 2, -1, 1, 0};
private final int[] state;
private final long[] stateLow;
private final long[] stateHigh;
private final int[] scratchpad = new int[STATE_LENGTH];
protected Curl(SpongeFactory.Mode mode) {
switch(mode) {
case CURLP27: {
numberOfRounds = NUMBER_OF_ROUNDSP27;
} break;
case CURLP81: {
numberOfRounds = NUMBER_OF_ROUNDSP81;
} break;
default: throw new NoSuchElementException("Only Curl-P-27 and Curl-P-81 are supported.");
}
state = new int[STATE_LENGTH];
stateHigh = null;
stateLow = null;
}
public void absorb(final int[] trits, int offset, int length) {
do {
System.arraycopy(trits, offset, state, 0, length < HASH_LENGTH ? length : HASH_LENGTH);
transform();
offset += HASH_LENGTH;
} while ((length -= HASH_LENGTH) > 0);
}
public void squeeze(final int[] trits, int offset, int length) {
do {
System.arraycopy(state, 0, trits, offset, length < HASH_LENGTH ? length : HASH_LENGTH);
transform();
offset += HASH_LENGTH;
} while ((length -= HASH_LENGTH) > 0);
}
private void transform() {
//final int[] scratchpad = new int[STATE_LENGTH];
int scratchpadIndex = 0;
int prev_scratchpadIndex = 0;
for (int round = 0; round < numberOfRounds; round++) {
System.arraycopy(state, 0, scratchpad, 0, STATE_LENGTH);
for (int stateIndex = 0; stateIndex < STATE_LENGTH; stateIndex++) {
prev_scratchpadIndex = scratchpadIndex;
if (scratchpadIndex < 365) {
scratchpadIndex += 364;
} else {
scratchpadIndex += -365;
}
state[stateIndex] = TRUTH_TABLE[scratchpad[prev_scratchpadIndex] + (scratchpad[scratchpadIndex] << 2) + 5];
}
}
}
public void reset() {
Arrays.fill(state, 0);
}
...
}
```
* [Kerl.java](https://github.com/iotaledger/iri/blob/dev/src/main/java/com/iota/iri/hash/Kerl.java)
```java=
public class Kerl implements Sponge {
public static final int HASH_LENGTH = 243;
public static final int BIT_HASH_LENGTH = 384;
public static final int BYTE_HASH_LENGTH = BIT_HASH_LENGTH / 8;
private byte[] byte_state;
private int[] trit_state;
private final Keccak.Digest384 keccak;
protected Kerl() {
this.keccak = new Keccak.Digest384();
this.byte_state = new byte[BYTE_HASH_LENGTH];
this.trit_state = new int[HASH_LENGTH];
}
@Override
public void reset() {
this.keccak.reset();
}
@Override
public void absorb(final int[] trits, int offset, int length) {
if (length % 243 != 0) throw new RuntimeException("Illegal length: " + length);
do {
//copy trits[offset:offset+length]
System.arraycopy(trits, offset, trit_state, 0, HASH_LENGTH);
//convert to bits
trit_state[HASH_LENGTH - 1] = 0;
byte[] bytes = bytesFromBigInt(bigIntFromTrits(trit_state, 0, HASH_LENGTH), BYTE_HASH_LENGTH);
//run keccak
keccak.update(bytes);
offset += HASH_LENGTH;
} while ((length -= HASH_LENGTH) > 0);
}
@Override
public void squeeze(final int[] trits, int offset, int length) {
if (length % 243 != 0) throw new RuntimeException("Illegal length: " + length);
do {
byte_state = this.keccak.digest();
//convert to trits
trit_state = tritsFromBigInt(bigIntFromBytes(byte_state,0,BYTE_HASH_LENGTH), HASH_LENGTH);
//copy with offset
trit_state[HASH_LENGTH - 1] = 0;
System.arraycopy(trit_state, 0, trits, offset, HASH_LENGTH);
//calculate hash again
for (int i = byte_state.length; i-- > 0; ) {
byte_state[i] = (byte) (byte_state[i] ^ 0xFF);
}
keccak.update(byte_state);
offset += HASH_LENGTH;
} while ((length -= HASH_LENGTH) > 0);
}
...
}
```
### 參考資料
* [The Transparency Compendium](https://blog.iota.org/the-transparency-compendium-26aa5bb8e260)
* [IOTA Vulnerability Report: Cryptanalysis of the Curl Hash Function Enabling Practical Signature Forgery Attacks on the IOTA Cryptocurrency](https://github.com/mit-dci/tangled-curl/blob/master/vuln-iota.md)
* [IOTA:Upgrades & Updates](https://blog.iota.org/upgrades-updates-d12145e381eb)([簡體中文版](http://www.iotachina.com/iotagengxinyushengjiyugao20170808.html))
* [IOTACHINA](http://www.iotachina.com/)
* [IOTA_Whitepaper](http://www.tangleblog.com/wp-content/uploads/2016/11/IOTA_Whitepaper.pdf)(中文版:[Tangle 白皮書](https://hackmd.io/c/rkpoORY4W/https%3A%2F%2Fhackmd.io%2Fs%2FB1YKzhbLb%23))
* [IOTA open source repos on GitHub](https://github.com/iotaledger)
* [Noob: Why 3nary encoding?](https://www.reddit.com/r/Iota/comments/5r72rh/noob_why_3nary_encoding/)
* [Curl disclosure, beyond the headline](https://blog.iota.org/curl-disclosure-beyond-the-headline-1814048d08ef)
* [Merged Kerl Implementation](https://github.com/iotaledger/iri/commit/539e413352a77b1db2042f46887e41d558f575e5)
* [Is the real value in IOTA its connection to the Jinn Ternary Processor?](https://www.reddit.com/r/Iota/comments/6kyk4v/is_the_real_value_in_iota_its_connection_to_the/)
* [物联网世界的基石 — IOTA](http://www.iotachina.com/iotazhengwentougaowenzhangwulianwangshijiedejishi-iota.html)
* [wikipedia:Sponge function](https://en.wikipedia.org/wiki/Sponge_function)
* [Cryptographic vulnerabilities in IOTA](https://medium.com/@neha/cryptographic-vulnerabilities-in-iota-9a6a9ddc4367)
* [IOTA研究](https://hackmd.io/s/HkMlibG6Z)
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet