Discontinuous Galerkin Methods
===
Min-Hung Chen [myCV](https://hackmd.io/pZR5oCNdTxqwRUrD_KbFlg)
---
# 參考資料：
## 數值偏微分方程
* [Finite Difference Methods for Ordinary and Partial Differential Equations by Randall J. LeVeque](http://faculty.washington.edu/rjl/fdmbook/)
* [am585winter06.pdf](https://www.dropbox.com/s/jle2ez5cxl5qbk9/am585winter06.pdf?dl=0)
* [am586spring06.pdf](https://www.dropbox.com/s/whn7bjytmahyntw/am586spring06.pdf?dl=0)
* [adssdada](https://colab.research.google.com/drive/18--Ex0go5q39oreoyCkCpH6vHyp1Xn-U?usp=sharing#scrollTo=fbXiO6GUJzle)
$$
\int f(x) e^x dx
$$
| Column 1 | Column 2 | Column 3 |
| -------- | -------- | -------- |
| Text | Text | Text |
## Finite Element Methods
* Numerical solution of partial differential equations by the finite element method by Claes Johnson
## Discontinuous Galerkin Methods
* Lecture Notes by Bernardo Cockburn: "An Introduction to the Discontinuous Galerkin method for Convection-Dominated Problems"
* A short essay on discontinuous Galerkin methods: Discontinuous Galerkin methods, ZAMM. Z. Angew. Math. Mech. 83 (2003), no. 11, 731-754.
* [舊課程網頁](http://www.math.ncku.edu.tw/~mhchen/syl_dg/syl_dg.html)
* [Discontinuous_Galerkin_method - wiki](https://en.wikipedia.org/wiki/Discontinuous_Galerkin_method)
* https://www.cfd-online.com/Wiki/Discontinuous_Galerkin
* http://lsec.cc.ac.cn/lcfd/DGM_mem.html (已停止更新)
* [Numerical Partial Differential Equations by Dr Tim Warburton](http://www.caam.rice.edu/~timwar/MA578S03/MA578.html) (Nodal DG方法)
----
* What is the Discontinuous Galerkin Method?:
* a method between a finite element and a finite volume method
* local to the generating element
* practical framework for the development of high-order accurate methods using unstructured grids
* History:
* Reed and Hill (1973): Triangular mesh methods for the neutron transport equation
* LeSaint and Raviart (1974): On a finite element method for solving the neutron transport equation.
* Cockburn and Shu (1989)
---
# Introduction
[Source](http://abstrusegoose.com/275)
----
[Source](http://nanodash.tumblr.com/post/80578032947/thegreekletterdelta-pokemon-as-described-by)
----
## 三種基本偏微分方程
* Advection Equation - 流體對流、波傳、電磁波
* Diffusiont Equation - 熱方程、擴散
* Elliptic Equation -
----
## Advection Equation
---
## Numerical Methods
### Finite Difference Methods
* [Finite Difference Methods for Ordinary and Partial Differential Equations by Randall J. LeVeque](http://faculty.washington.edu/rjl/fdmbook/)
* [am585winter06.pdf](https://www.dropbox.com/s/jle2ez5cxl5qbk9/am585winter06.pdf?dl=0)
* [am586spring06.pdf](https://www.dropbox.com/s/whn7bjytmahyntw/am586spring06.pdf?dl=0)
### Finite Element Methods
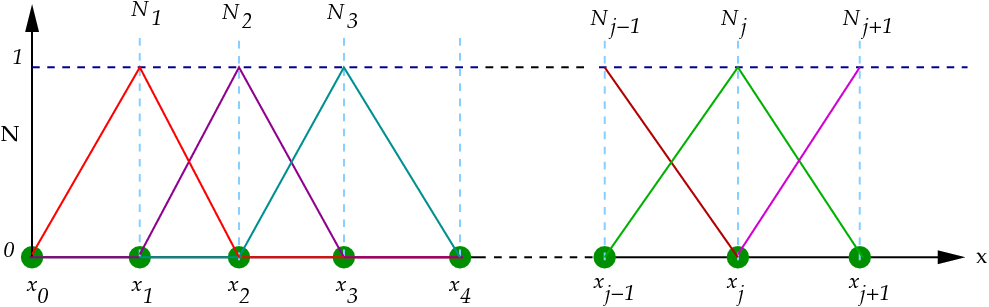
* Basis function - 1D Example
# Discontinuous Galerkin Methods
Notes: [A short essay on discontinuous Galerkin methods: Discontinuous Galerkin methods, ZAMM. Z. Angew. Math. Mech. 83 (2003), no. 11, 731-754.](https://www.dropbox.com/s/4n83fk5yzesps8d/Cockburn2003DGMethods.pdf?dl=0)
## DG for solving linear ODE
* [Legendre Polynomial -wolfram](http://mathworld.wolfram.com/LegendrePolynomial.html)
* [Legendre Polynomial -wiki](https://en.wikipedia.org/wiki/Legendre_polynomials)
* [gauleg.m](https://www.dropbox.com/s/pnre0qg3teky4ts/gauleg.m?dl=0)
* [legtable.m](https://www.dropbox.com/s/pxmkt7s2dqwts3r/legtable.m?dl=0)
* [dg_ode.zip](https://www.dropbox.com/s/oczok0tm3f432my/dg_ode.zip?dl=0)
----
### Notes
#### Date:2017-03-06
\begin{align}
\frac{du(t)}{dt} & = f(t)u(t), \quad t\in (0,T) , \quad u(x,t=0) = u_{0}.
\end{align}
\begin{align*}
\frac{du(t)}{dt} \ {\color{red} v(t)} & = f(t)u(t) \ {\color{red} v(t)}
\end{align*}
\begin{align}
\int_{I^{n}} \frac{du_{h}(s)}{ds} v(s)\,ds & = \int_{I^n} f(s)u_{h}(s) \, v(s)\, ds, \quad I^{n} = (t^{n}, t^{n+1}) \\
t^{0} & = 0, \quad t^{N} = T, \quad n = 0, \dots, N-1. \nonumber
\end{align}
Integration by parts
$$
\widehat{u_{h}}(s) \, v(s) \bigg|_{t^{n}}^{t^{n+1}} - \int_{I^{n}} u_{h}(s)
\frac{dv(s)}{ds} \, ds = \int_{I^n} f(s)u_{h}(s) \, v(s)\, ds
$$
where
\begin{align}
\widehat{u}_{h}(t^{n})
& = \{\begin{array}{l}
u_{0}, \quad \text{if} \quad t^{n} = 0, \\
\lim\limits_{\epsilon\rightarrow 0} u_{h}(t^{n} - \epsilon) , \quad \text{ow}. \quad
\end{array}
\end{align}
\begin{align}
\Rightarrow \sum\limits_{n=0}^{N-1} \widehat{u}_{h}(s) \ v(s) \bigg|_{t^{n}}^{t^{n+1}} -
\sum\limits_{n=0}^{N-1} \int_{I^{n}} u_{h}(s) \frac{dv(s)}{ds} \ ds =
\sum\limits_{n=0}^{N-1} \int_{I^n} f(s)u_{h}(s) \ v(s)\ ds
\end{align}
Take $v(s)=u_{h}(s)$
\begin{align}
\sum\limits_{n=0}^{N-1} \widehat{u}_{h}(s) \ u_{h}(s)
|_{t^{n}}^{t^{n+1}} -
\sum\limits_{n=0}^{N-1} \int_{I^{n}} u_{h}(s) \frac{du_{h}(s)}{ds} \ ds =
\sum\limits_{n=0}^{N-1} \int_{I^n} f(s) \ u_{h}^2(s)\ ds
\end{align}
\begin{align}
\sum\limits_{n=0}^{N-1} \widehat{u}_{h}(s) \ u_{h}(s) |_{t^{n}}^{t^{n+1}} -
\sum\limits_{n=0}^{N-1} \int_{I^{n}} \frac{d}{ds}
( \frac{1}{2} u_{h}^2(s) ) \ ds
= \sum\limits_{n=0}^{N-1} \int_{I^n} f(s) \ u_{h}^2(s) \ ds
\end{align}
\begin{align}
\sum\limits_{n=0}^{N-1} \widehat{u}_{h}(s) \ u_{h}(s) |_{t^{n}}^{t^{n+1}} -
\sum\limits_{n=0}^{N-1} \frac{1}{2} u_{h}^2(s) \ |_{t^{n}}^{t^{n+1}}
= \sum\limits_{n=0}^{N-1} \int_{I^n} f(s) \ u_{h}^2(s) \ ds
\end{align}
\begin{align*}
\{u_{h}\} & = \frac{1}{2} \big( u_{h}^{-} + u_{h}^{+} \big) \nonumber \\
[[ u_{h}]] & = u_{h}^{-} - u_{h}^{+} \nonumber \\
u_{h}^{\pm}(t^{n}) & =
\lim\limits_{\epsilon\rightarrow 0} u_{h}^{\pm}(t^{n} \pm \epsilon)
\end{align*}
\begin{align*}
\{u_{h}\} [[ u_{h} ]] & = \frac{1}{2} \big( u_{h}^{-} + u_{h}^{+} \big) \big( u_{h}^{-} - u_{h}^{+} \big) \nonumber \\
& = \frac{1}{2} \big( u_{h}^{-2} - u_{h}^{+2} \big) \nonumber \\
& = \frac{1}{2} [[ u_{h}^2 ]] \nonumber
\end{align*}
#### Notation:
\begin{align*}
\widehat{u}_{h}(t^{n}) &=
u_{h}^{-} (t^{n}), \quad \text{if} \quad t^{n} \neq 0 \\
\{u_{h}(t^{n})\} &= \frac{1}{2} \bigg( u_{h}^{-} (t^{n}) + u_{h}^{+} (t^{n}) \bigg), \quad \{\,\}=\text{Average}
\\
[[ u_{h}(t^{n}) ]] &= u_{h}^{-} (t^{n}) - u_{h}^{+} (t^{n}), \quad [[\,]] =\text{Jump}
\end{align*}
\begin{align}
\sum\limits_{n=0}^{N-1} \widehat{u}_{h}(s) \ u_{h}(s) \ \bigg|_{t^{n}}^{t^{n+1}} =
& \big({\widehat{u}}_{h}^{I^{0}}\big)(t^{1})\big(u_{h}^{I^{0}}\big) (t^{1}) - \big(\widehat{u}_{h}^{I^{0}}\big)(t^{0})\big(u_{h}^{I^{0}}\big) (t^{0})
\quad + \nonumber \\
& \big(\widehat{u}_{h}^{I^{1}}\big) (t^{2})\big(u_{h}^{I^{1}}\big) (t^{2})- \big(\widehat{u}_{h}^{I^{1}}\big) (t^{1})\big(u_{h}^{I^{1}}\big) (t^{1})
\quad + \nonumber \\
& \qquad \qquad \qquad \vdots \qquad \qquad \qquad
\quad + \nonumber \\
& \big(\widehat{u}_{h}^{I^{N-2}}\big) (t^{N-1})\big(u_{h}^{I^{N-2}}\big) (t^{N-1})- \big(\widehat{u}_{h}^{I^{N-2}}\big) (t^{N-2})\big(u_{h}^{I^{N-2}}\big) (t^{N-2}) \quad + \nonumber \\
& \big(\widehat{u}_{h}^{I^{N-1}}\big) (t^{N})\big(u_{h}^{I^{N-1}}\big) (t^{N})- \big(\widehat{u}_{h}^{I^{N-1}}\big) (t^{N-1})\big(u_{h}^{I^{N-1}}\big) (t^{N-1}) \nonumber \\
= & \big(\widehat{u}_{h}^{I^{N-1}}\big) (t^{N})\big(u_{h}^{I^{N-1}}\big) (t^{N})- \big(\widehat{u}_{h}^{I^{0}}\big) (t^{0}) \big(u_{h}^{I^{0}}\big) (t^{0})
\quad + \nonumber \\
& \big(\widehat{u}_{h}^{I^{0}}\big) (t^{1})\big(u_{h}^{I^{0}}\big) (t^{1})- \big(\widehat{u}_{h}^{I^{1}}\big) (t^{1})\big(u_{h}^{I^{1}}\big) (t^{1})
\quad + \nonumber \\
& \qquad \qquad \qquad \vdots \qquad \qquad \qquad
\quad + \nonumber \\
& \big(\widehat{u}_{h}^{I^{N-3}}\big) (t^{N-2})\big(u_{h}^{I^{N-3}}\big) (t^{N-2})- \big(\widehat{u}_{h}^{I^{N-2}}\big) (t^{N-2})\big(u_{h}^{I^{N-2}}\big) (t^{N-2}) \quad + \nonumber \\
& \big(\widehat{u}_{h}^{I^{N-2}}\big) (t^{N-1})\big(u_{h}^{I^{N-2}}\big) (t^{N-1})- \big(\widehat{u}_{h}^{I^{N-1}}\big) (t^{N-1})\big(u_{h}^{I^{N-1}}\big) (t^{N-1})\nonumber \\
\end{align}
\begin{align}
= & \big(\widehat{u}_{h}\big) (T) \big(u_{h}^{-}\big) (T) - \big(\widehat{u}_{h}\big) (0) \big(u_{h}^{+}\big) (0) + \sum\limits_{n=1}^{N-1} \widehat{u}_{h} [[ u_{h} ]]
\end{align}
\begin{align}
\sum\limits_{n=0}^{N-1} \frac{1}{2} u_{h}^2(s) \ \bigg|_{t^{n}}^{t^{n+1}} =
\frac{1}{2} \bigg [
& \big(u_{h}^{I^{0}}\big)^{2} (t^{1}) - \big(u_{h}^{I^{0}}\big)^{2} (t^{0}) \quad + \nonumber \\
& \big(u_{h}^{I^{1}}\big)^{2} (t^{2}) - \big(u_{h}^{I^{1}}\big)^{2} (t^{1}) \quad + \nonumber \\
& \qquad \qquad \qquad \vdots \qquad \qquad \qquad \quad + \nonumber \\
& \big(u_{h}^{I^{N-2}}\big)^{2} (t^{N-1}) - \big(u_{h}^{I^{N-2}}\big)^{2} (t^{N-2}) \quad + \nonumber \\
& \big(u_{h}^{I^{N-1}}\big)^{2} (t^{N}) - \big(u_{h}^{I^{N-1}}\big)^{2} (t^{N-1}) \bigg ] \nonumber \\
= \frac{1}{2} \bigg [
& \big(u_{h}^{I^{N-1}}\big)^{2} (t^{N}) - \big(u_{h}^{I^{0}}\big)^{2} (t^{0}) \quad + \nonumber \\
& \big(u_{h}^{I^{0}}\big)^{2} (t^{1}) - \big(u_{h}^{I^{1}}\big)^{2} (t^{1}) \quad + \nonumber \\
& \qquad \qquad \qquad \vdots \qquad \qquad \qquad \quad + \nonumber \\
& \big(u_{h}^{I^{N-3}}\big)^{2} (t^{N-2}) - \big(u_{h}^{I^{N-2}}\big)^{2} (t^{N-2}) \quad + \nonumber \\
& \big(u_{h}^{I^{N-2}}\big)^{2} (t^{N-1}) - \big(u_{h}^{I^{N-1}}\big)^{2} (t^{N-1}) \bigg ] \nonumber \\
= \frac{1}{2} \bigg [
& \big(u_{h}^{-}\big)^{2} (T) - \big(u_{h}^{+}\big)^{2} (0) \bigg ] + \sum\limits_{n=1}^{N-1} \frac{1}{2}[[u_{h}^2 ]]
\end{align}
Then,
\begin{align}
\sum\limits_{n=1}^{N-1} \bigg(
\widehat{u}_{h} [[ u_{h}]] - \frac{1}{2} [[u_{h}^2]] \bigg)
& = \sum\limits_{n=1}^{N-1} \bigg(
\widehat{u}_{h} [[ u_{h}]] - \{u_{h}\} [[u_{h}]] \bigg) \\
& = \sum\limits_{n=1}^{N-1}
\bigg( \widehat{u}_{h} - \{u_{h}\}\bigg) [[u_{h}]]
= \sum\limits_{n=1}^{N-1}
C [[ u_{h}]]^{2} \geq 0
\end{align}
\begin{align*}
\widehat{u}_{h}(t^{n})
& = \Bigg\{ \begin{array}{l}
u_{0}, \quad \text{if} \quad t^{n} = 0, \\
\{u_{h}\} + C [[u_{h}]], \quad \text{if} \quad t^{n} \in(0,T), \quad C \geq 0, \quad C = \frac{1}{2} \quad \text{Upwinding Scheme} \\
u_{h}^{-}(T), \quad \text{if} \quad t^{n} =T.
\end{array}
\end{align*}
Take a break
[DG for solving linear ODE]
\begin{align*}
\text{orthonormal:}\quad
{\int}_{I^{n}}& \varphi_{i}(s)\varphi_{j}(s) \,ds = \delta_{ij} \\
\text{orhogonal:}\quad
{\int}_{I^{n}}& \varphi_{i}(s)\varphi_{j}(s) \,ds\, \Bigg\{
\begin{array}{l}
= 0, \quad \text{if} \quad i \neq j, \\
\neq 0, \quad \text{if} \quad i = j.\\
\end{array} \\
(f,g) = {\int}_{I^{n}}& f(s)g(s)\,ds \\
\lVert f \rVert_{2} = \bigg[ {\int}_{I^{n}}& f^2(s)\,ds \bigg]^{1/2} \\
\end{align*}
#### Date:2017-03-13
[Upwinding Numerical Flux]
\begin{align*}
\widehat{u}_{h}(s) v(s) \bigg|_{t^{n}}^{t^{n+1}} - \int_{I^{n}} u_{h}(s) \frac{dv(s)}{ds} ds = \int_{I^{n}} f(s)u_{h}(s) v(s) ds
\end{align*}
\begin{align*}
V_{h}^{n} &= \text{span} \{\varphi_{i}^{n}\} \\
u_{h}(t) \bigg|_{I^{n}} & =
\sum\limits_{j=0}^{k} a_{j}^{n} \varphi_{j}^{n}(t) \\
\text{Take} \quad v(t) \bigg|_{I^{n}} & =
\varphi_{i}^{n}(t)
\end{align*}
Find $u_{h}(t) \in V_{h}$ st $u_{h}(t)$ satisfying Eq. for all $v(t) \in V_{h}$
\begin{align*}
\widehat{u}_{h}(t^{n})
& = \Bigg\{
\begin{array}{l}
u_{0}, \quad \text{if} \quad t^{n} = 0, \\
\lim\limits_{\epsilon\rightarrow 0} u_{h}(t^{n} - \epsilon) , \quad \text{ow}. \quad
\end{array}
\end{align*}
\begin{align*}
\Rightarrow \widehat{u}_{h}(t^{n+1}) v(t^{n+1}) - \widehat{u}_{h}(t^{n}) v(t^{n}) - \int_{I^{n}} u_{h}(s) \frac{dv(s)}{ds} ds = \int_{I^{n}} f(s)u_{h}(s) v(s) ds\
\end{align*}
\begin{align*}
\sum\limits_{j=0}^{k} a_{i}^{n} \varphi_{j}^{n}(t^{n+1}) \ \varphi_{i}^{n}(t^{n+1}) & - \sum\limits_{j=0}^{k} a_{j}^{n-1} \varphi_{j}^{n-1} (t^{n}) \ \varphi_{i}^{n}(t^{n}) - \int_{I^{n}} \sum\limits_{j=0}^{k} a_{j}^{n} \varphi_{j}^{n}(s) \frac{d\varphi_{i}^{n}(s)}{ds} \ ds \\
& = \int_{I^{n}} f(s)\sum\limits_{j=0}^{k} a_{j}^{n} \varphi_{j}^{n}(s) \ \varphi_{i}^{n}(s)\ ds\
\end{align*}
We have to know $u_{h}^{-}(t^{n})$
\begin{align*}
\sum\limits_{j=0}^{k} a_{j}^{n} \varphi_{j}^{n}(t^{n+1}) \ \varphi_{i}^{n}(t^{n+1}) & - \sum\limits_{j=0}^{k} a_{j}^{n-1} \varphi_{j}^{n-1} (t^{n}) \ \varphi_{i}^{n}(t^{n}) - \sum\limits_{j=0}^{k} a_{j}^{n} \int_{I^{n}} \varphi_{j}^{n}(s) \frac{d\varphi_{i}^{n}(s)}{ds} \ ds \\
& = \sum\limits_{j=0}^{k} a_{j}^{n} \int_{I^{n}} f(s) \varphi_{j}^{n}(s) \ \varphi_{i}^{n}(s)\ ds\
\end{align*}
\begin{align*}
\sum\limits_{j=0}^{k} a_{j}^{n} \varphi_{j}^{n}(t^{n+1}) \ \varphi_{i}^{n}(t^{n+1}) & - \sum\limits_{j=0}^{k} a_{j}^{n} \int_{I^{n}} \varphi_{j}^{n}(s) \frac{d\varphi_{i}^{n}(s)}{ds} \ ds -\sum\limits_{j=0}^{k} a_{j}^{n} \int_{I^{n}} f(s) \varphi_{j}^{n}(s) \ \varphi_{i}^{n}(s)\ ds \\
& = \sum\limits_{j=0}^{k} a_{j}^{n-1} \varphi_{j}^{n-1} (t^{n}) \ \varphi_{i}^{n}(t^{n})
\end{align*}
\begin{align*}
\bigg[ \varphi_{i}^{n}(t^{n+1}) \varphi_{j}^{n}(t^{n+1}) \bigg] \bigg[ a_{j}^{n} \bigg] & - \bigg[ \int_{I^{n}} \frac{d\varphi_{i}^{n}(s)}{ds} \,\varphi_{j}^{n}(s) \,ds\, \bigg] \bigg[ a_{j}^{n} \bigg] - \bigg[ \int_{I^{n}} \varphi_{i}^{n}(s)\,f(s)\,\varphi_{j}^{n}(s) \,ds\, \bigg] \bigg[ a_{j}^{n} \bigg] \\
& = \bigg[ \varphi_{i}^{n}(t^{n}) \, \varphi_{j}^{n-1} (t^{n}) \bigg] \bigg[ a_{j}^{n-1} \bigg]
\end{align*}
\begin{align*}
l_{ij} &= \bigg[ \varphi_{i}^{n}(t^{n+1}) \varphi_{j}^{n}(t^{n+1}) \bigg] \\
m_{ij} &= \bigg[ \int_{I^{n}} \frac{d\varphi_{i}^{n}(s)}{ds} \varphi_{j}^{n}(s) ds \bigg] \\
f_{ij} &= \bigg[ \int_{I^{n}} \varphi_{i}^{n}(s)f(s)\varphi_{j}^{n}(s) ds \bigg] \quad \\
g_{ij} &= \bigg[ \varphi_{i}^{n}(t^{n}) \varphi_{j}^{n-1} (t^{n}) \bigg] \\
\big[ l_{ij} \big] \big[ a_{j}^{n} \big] - \big[ m_{ij} \big] \big[ a_{j}^{n} \big] - \big[ f_{ij} \big] \big[ a_{j}^{n} \big]
&= \big[ g_{ij} \big] \big[ a_{j}^{n-1} \big]
\end{align*}
\begin{align*}
\big[ \mathbf{L-M-F} \big] \big[ \mathbf{A} \big]
&= \big[ \mathbf{G} \big]
\end{align*}
----
\begin{align*}
\varphi_{i}^{n}(t) &= P_{i} \bigg( \frac{2t-t^{n+1}-t^{n}}{t^{n+1}-t^{n}}\bigg) \\
l_{ij} &= \bigg[ \varphi_{i}^{n}(t^{n+1}) \ \varphi_{j}^{n}(t^{n+1}) \bigg] = (1)^{i}(1)^{j} = 1 \\
m_{ij} &= \bigg[ \int_{I^{n}} \frac{d\varphi_{i}^{n}(s)}{ds} \,\varphi_{j}^{n}(s) \,ds\, \bigg] \\
& = \Bigg\{
\begin{array}{l}
{\color{blue}2, \quad \text{if} \quad i>j, \quad \text{and} \quad i-j = \text{odd} } \\
0, \quad \text{otherwise}.
\end{array} \\
g_{ij} &= \bigg[ \varphi_{i}^{n}(t^{n}) \, \varphi_{j}^{n-1} (t^{n}) \bigg] = (-1)^{i}(1)^{j} = (-1)^{i}
\end{align*}
\begin{align*}
\varphi_{i}^{n}(t^{n+1}) &= (1)^{i} \\
\varphi_{j}^{n}(t^{n+1}) &= (1)^{j} \\
\varphi_{i}^{n}(t^{n}) &= (-1)^{i} \\
\varphi_{j}^{n-1} (t^{n}) &= (1)^{j}
\end{align*}
----
\begin{align*}
P_{n}(1) &= 1 \\
P_{n}(-s) &= (\pm1)^{n} P_{n}(s)\\
P_{n}(\pm1) &= (\pm1)^{n} \\
P_{n}^{\prime}(\pm1) &= (\pm1)^{n} \, \frac{n(n+1)}{2}\\
\int_{-1}^{1} P_{m}(s) P_{n}(s)\, ds &= \frac{2}{2n+1} \delta_{mn} \\
\end{align*}
----
\begin{align*}
\int_{a}^{b} f(t)\,dt &= \frac{b-a}{2}
\int_{-1}^{1} f\big( \frac{b-a}{2} s + \frac{b+a}{2} \big)ds \\
\approx & \frac{b-a}{2} \sum\limits_{l=1}^{m}
w_{l} f\big( \frac{b-a}{2} s_{l} + \frac{b+a}{2} \big) \\
t &= \frac{b-a}{2} s + \frac{b+a}{2} \\
s &= \frac{2}{b-a} \big( t- \frac{b+a}{2} \big) \\
f\big( \frac{b-a}{2} s + \frac{b+a}{2} \big) &= \sum\limits_{j=0}^{k} c_{j} P_{j} (s) \\
\int_{-1}^{1} P_{j}(s) P_{j}(s)\, ds &= \frac{2}{2j+1} \\
c_{i} &= \frac{2i+1}{2} \int_{-1}^{1} f\big( \frac{b-a}{2} s + \frac{b+a}{2} \big)\,P_{i}(s)\,ds \\
&= \frac{2i+1}{2} \sum\limits_{l=1}^{m}
w_{l} f\big( \frac{b-a}{2} s_{l} + \frac{b+a}
{2} \big)P_{i}(s_{l}) \\
\end{align*}
---
## Homework 0
### Space Discretization
Divide $[0,2]$ into subintervals, $\{ I^n \}_{n=0}^{N-1}$, where $I^n=[t^n,t^{n+1}]$, $t^n = nh$ and $h=(2-0)/N$.
### Basis Expansion
假設在每個區間上，我們希望將給定的函數$f$投影到在$k$次多項式空間
，也就是說在$I^n=[t^n,t^{n+1}]$區間，我們希望$f$可以用基底函數展開，
$$f|_{I^n}\approx \sum_{j=0}^k c_j^n \phi_j^n (t), \quad t \in I^n=[t^n,t^{n+1}], $$
其中$\phi_j^n$是基底函數，同時上標$n$表示位在$I^n$區間。在本次作業中，我們使用一線性映射以及Legendre polynomial至造出該基底函數:
$$\phi_j^n(t)=P_j(s(t)), \quad s(t) =\frac{2t-t^{n+1}-t^n}{t^{n+1}-t^n},\quad t \in I^n,$$
or
$$P_j(s)=\phi_j^n(t(s)), \quad t(s) =\frac{t^{n+1}-t^n}{2}s+\frac{t^{n+1}+t^n}{2},\quad s \in [-1,1].$$
欲取得係數$c_j^n$，可將$f$乘上基底函數$\phi_i^n$在$I^n$積分，則我們可以得到下式
$$
\int_{I^n} f(t)\phi_i^n(t)\,dt \approx\int_{I^n} \sum_{j=0}^k c_j^n \phi_j^n(t) \phi_i^n(t)\, dt
=c_i^n \frac{2}{2i+1} \frac{t^{n+1}-t^n}{2}
$$
令函數$f_h$表示函數$f$在每個區間投影至$k$次多項式空間的結果，也就是說
\begin{eqnarray}
f_h|_{I^n}&=& \sum_{j=0}^k c_j^n \phi_j^n (t),\\
c_i^n &=&\frac{2i+1}{t^{n+1}-t^n}\int_{I^n} f(t)\phi_i^n(t)\,dt\\
&=&\frac{2i+1}{t^{n+1}-t^n}\frac{t^{n+1}-t^n}{2}\int_{-1}^1 f(t(s))\phi_i^n(t(s))\,ds\\
&=&\frac{2i+1}{2}\sum_{l=1}^{m} w_l f(t(s_l))\phi_i^n(t(s_l)) \\
\end{eqnarray}
1.令$f=1+t+t^2+t^3+t^4$, $t \in [0,2]$
* 計算$f_h$的$L^2$誤差:
$$
\left(\int_0^2 (f(t)-f_h(t))^2 \,dt\right)^{1/2}=\left(\sum_{n=0}^{N-1}\int_{I^n} (f(t)-f_h(t))^2 \,dt\right)^{1/2}
$$
* 畫出$f_h$以及$f$
2.令$f(t)=e^t$
* 計算$f_h$的誤差:
* 畫出$f_h$以及$f$
---
## Homework 1
Consider the initial value problem,
$$
\frac{d}{dt}u=e^t, \quad t\in [0,2], \quad u(0)=1.
$$
### Space Discretization
Divide $[0,2]$ into subintervals, $\{ I^n \}_{n=0}^{N-1}$, where $I^n=[t^n,t^{n+1}]$, $t^n = nh$ and $h=(2-0)/N$.
### Basis Function - Legendre Polynomial
假設 $P_n(x)$ 是n次的Legendre Polynomial (on $[-1,1]$)
1. 使用linear mapping,$T(t)$,製造出定義在$I^n=[t^n,t^{n+1}]$上的基底函數:$\phi_j(t)=P_j(T(t))$, $t \in I^n$
2. 計算$\int_{I^n} \phi_j(t) \phi_i'(t)\, dt$
3. 使用 gauleg.m, legtable.m 寫一個matlab程式計算$\int_{I^n} \phi_j(t) \phi_i'(t)\, dt$
4. 使用 gauleg.m, legtable.m 寫一個matlab程式計算$\int_{I^n} f(t) \phi_i(t)\, dt$
### DG methods for solving ODE
以Legendre polynomial做為基底，以DG方法(note的2,3式)對ODE求解
$$
\frac{d}{dt}u=e^t, \quad t\in [0,2], \quad u(0)=1.
$$
1. Compute the $L^2$-errors of the numerical solutions. What is the rate of convergence?
2. Compute the Nodal errors of the numerical solutions. What is the rate of convergence?
3. Discuss the results.
參考資料：
* [Note: Discontinuous Galerkin methods, ZAMM. Z. Angew. Math. Mech. 83 (2003), no. 11, 731-754.](https://www.dropbox.com/s/4n83fk5yzesps8d/Cockburn2003DGMethods.pdf?dl=0)
* [簡介投影片](https://www.dropbox.com/s/r1ppfs4bnlp4v5v/sc1029.pdf?dl=0)
#### Details
$$
\frac{d}{dt}u=f(t), \quad t\in [0,2], \quad u(0)=u_0.
$$
##### DG Scheme
$$
-\int_{I^n} u_h(s) \frac{d}{dt}v(s)\, ds +\widehat{u_h}v|_{t^n}^{t^{n+1}}=\int_{I^n} f(s)v(s)\,ds,$$
$$
\widehat{u_h}(t^n)=\{
\begin{array}{ll}
u_0, &if\quad t^n =0,\\
u_h^{n-1}(t^n), &otherwise.
\end{array}
$$
##### Basis Expansion
假設在每個區間上，我們希望可以在$k$次多項式空間中找到一解$u_h$近似微分方程的解，$u$。則在$I^n=[t^n,t^{n+1}]$區間，$u_h$可以用基底函數展開，也就是說:
$$u_h|_{I^n}= \sum_{j=0}^k a_j^n \phi_j^n (t), \quad t \in I^n=[t^n,t^{n+1}], $$
其中$\phi_j^n$是基底函數，同時上標$n$表示位在$I^n$區間。在本次作業中，我們使用一線性映射以及Legendre polynomial至造出該基底函數:
$$\phi_j^n(t)=P_j(\frac{2t-t^{n+1}-t^n}{t^{n+1}-t^n}),\quad t \in I^n.$$
將 $u_h|_{I^n}= \sum_{j=0}^k a_j^n \phi_j^n (t)$同時取$v=\phi_i^n$，則我們可以得到下式
\begin{eqnarray}
-\int_{I^n} \sum_{j=0}^k a_j^n \phi_j^n(s) \frac{d}{dt}\phi_i^n(s)\, ds &+&\sum_{j=0}^k a_j^n \phi_j^n (t^{n+1})\phi_i^n(t^{n+1})\\
-\sum_{j=0}^k a_j^{n-1} \phi_j^{n-1} (t^{n})\phi_i^n(t^{n})&=&\int_{I^n} f(s)\phi_i^n(s)\,ds,
\end{eqnarray}
若在$I^0$區間，可得
\begin{eqnarray}
&-&\int_{I^0} \sum_{j=0}^k a_j^0 \phi_j^0(s) \frac{d}{dt}\phi_i^0(s)\, ds +\sum_{j=0}^k a_j^0 \phi_j^0 (t^{1})\phi_i^0(t^{1})
-u_0\phi_i^0(t^{0})\\
&=&\int_{I^0} f(s)\phi_i^0(s)\,ds.
\end{eqnarray}
假設我們要在$I^n$上求解，也就是說求係數$\{a_j^n\}$。則$\{a_j^{n-1}\}$已知，上式可改寫為
\begin{eqnarray}
-\sum_{j=0}^k a_j^n\int_{I^n} \phi_j^n(s) \frac{d}{dt}\phi_i^n(s)\, ds &+&\sum_{j=0}^k a_j^n \phi_j^n (t^{n+1})\phi_i^n(t^{n+1})\\
=\sum_{j=0}^k a_j^{n-1} \phi_j^{n-1} (t^{n})\phi_i^n(t^{n})&+&\int_{I^n} f(s)\phi_i^n(s)\,ds.
\end{eqnarray}
我們可以用矩陣方程表示：
$(-M+L)A = G+F$
或是
$(-m_{ij}+l_{ij})a_j = (g_i +f_i)$
其中
$m_{ij}=\int_{I^n} \phi_j^n(s) \frac{d}{dt}\phi_i^n(s)\, ds=\left\{
\begin{array}{ll}
2& if\quad i>j,\, and \quad i-j = odd\\
0& otherwise,
\end{array}
\right.$
$l_{ij}=\phi_j^n (t^{n+1})\phi_i^n(t^{n+1})=1$ (注意Legendre多項式在 1 的值為1)
$g_i = \sum_{j=0}^k a_j^{n-1} (1) (-1)^i$
$f_i = \int_{I^n} f(s)\phi_i^n(s)\,ds.$
以三次多項式函數空間為例，
$M = \left[\begin{array}{cccc}
0& 0& 0& 0\\
2& 0& 0& 0\\
0& 2& 0& 0\\
2& 0& 2& 0
\end{array}
\right]$
$L = \left[\begin{array}{cccc}
1& 1& 1& 1\\
1& 1& 1& 1\\
1& 1& 1& 1\\
1& 1& 1& 1
\end{array}
\right]$
---
## Homework
[Homework (pdf file)](https://www.dropbox.com/s/lc6zgw9lje3vhw6/DG_Hw1.pdf?dl=0)
Consider the initial value problem,
$$
\frac{d}{dt}u=f(t)u(t), \quad t\in (0,2), \quad u(0)=u_0.
$$
Write a code to solve the initial value problem using Discontinuous Galerkin methdos with Legedre polynomials as basis functios.
### Part 1
Solve the problem with various grid size and
$$f(t)=e^t, \quad u_0=1$$.
* Compute the $L^2$-errors of the numerical solutions. What is the rate of convergence?
* Compute the Nodal errors of the numerical solutions. What is the rate of convergence?
* Discuss the results.
### Part 2
Solve the problem with various grid size and
$$f(t)=
\left\{\begin {array}{c c}
t&0\le t \le 1\\
e^{t-1}& 1<t<2
\end{array} \right. \quad u_0=1
$$.
* Compute the $L^2$-errors of the numerical solutions. What is the rate of convergence?
* Compute the Nodal errors of the numerical solutions. What is the rate of convergence?
* Discuss the results.
## DG for solving linear Advection Equation
* [數值偏微分方程.pdf](https://www.dropbox.com/s/b8mhq800so9nvg6/%E6%95%B8%E5%80%BC%E5%81%8F%E5%BE%AE%E5%88%86%E6%96%B9%E7%A8%8B.pdf?dl=0)
* [Strong Stability-Preserving High-Order Time Discretization Methods∗](http://www.cscamm.umd.edu/tadmor/pub/linear-stability/Gottlieb-Shu-Tadmor.SIREV-01.pdf)(P95 Eq3.1-3.2)
* [dg_advection.zip](http://math.ncku.edu.tw/~mhchen/DG/dg_advection.zip)
### Notes
#### Date:2017-03-20
\begin{align}
u_{t} + a u_{x} &=0, \quad a>0, \quad a=\text{constant}, \quad x\in (0,1) \\
& u(x=0,t) = u_{0}(t).
\end{align}
\begin{align*}
\int_{0}^{1} u u_{t} \,dx &= - \int_{0}^{1} u a u_{x} \,dx \\
\int_{0}^{1} \partial_{t} \bigg( \frac{1}{2} u^{2} \bigg) \,dx &= - a \int_{0}^{1} \partial_{x} \bigg( \frac{1}{2} u^{2} \bigg) \,dx \\
\partial_{t} \int_{0}^{1} \frac{1}{2} u^{2} \,dx
&= - \frac{1}{2} a u^{2} \bigg|_{0}^{1} \\
&= - \frac{1}{2} a u^{2} (1) + \frac{1}{2} a u^{2} (0)
\end{align*}
------------
\begin{align*}
\int_{0}^{1} u u_{t} \,dx &+ \int_{0}^{1} u a u_{x} \,dx = 0 \\
\int_{0}^{1} \partial_{t} \bigg( \frac{1}{2} u^{2} \bigg) \,dx &+ a \int_{0}^{1} \partial_{x} \bigg( \frac{1}{2} u^{2} \bigg) \,dx =0 \notag \\
\partial_{t} \int_{0}^{1} \frac{1}{2} u^{2} \,dx &+ \frac{1}{2} a u^{2} \bigg|_{0}^{1} = 0 \\
\int_{0}^{T} \partial_{t} \int_{0}^{1} \frac{1}{2} u^{2} \,dx \,dt &+ \int_{0}^{T} \frac{1}{2} a u^{2} \bigg|_{0}^{1} \,dt =0 \\
\int_{0}^{1} \frac{1}{2} u^{2} (x,T) \,dx &- \int_{0}^{1} \frac{1}{2} u^{2} (x,0) \,dx + \int_{0}^{T} \frac{1}{2} a u^{2} \bigg|_{0}^{1} \,dt =0
\end{align*}
------------
\begin{align*}
u_{t} v + a u_{x} v &=0 \\
\int_{I_{j}} u_{t} v \,dx +
\int_{I_{j}} (a u)_{x} v \,dx &=0,
\quad I_{j} = [ x_{j}, x_{j+1} ] \\
x_{0} = 0, \quad x_{N} = 1, \quad j &= 0, \dots, N-1.
\end{align*}
integration by parts
\begin{align*}
\int_{I_{j}} u_{t} v \,dx &-
\int_{I_{j}} (a u) v_{x} \,dx +
(au) \, {\color{red} v} \bigg|_{x_{j}}^{x_{j+1}} =0
\end{align*}
Take $u=u_{h}$, $\Rightarrow$
\begin{align*}
\int_{I_{j}} \partial_{t} u _{h} v \,dx &-
\int_{I_{j}} (a u_{h}) v_{x} \,dx +
(\widehat{au_{h}}) \, v \bigg|_{x_{j}}^{x_{j+1}} =0
\end{align*}
Take $v=u_{h}$, $\Rightarrow$
\begin{align*}
\int_{I_{j}} u_{h} \partial_{t} u_{h} \,dx &- \int_{I_{j}} (a u_{h}) \partial_{x}u_{h} \,dx + (\widehat{au_{h}}) \, u_{h} \bigg|_{x_{j}}^{x_{j+1}} =0 \\
\int_{I_{j}} \partial_{t} \bigg( \frac{1}{2} u_{h}^{2} \bigg) \,dx &- \int_{I_{j}} \partial_{x} \bigg( \frac{1}{2} a u_{h}^{2} \bigg) \,dx + (\widehat{au_{h}}) \, u_{h} \bigg|_{x_{j}}^{x_{j+1}} =0 \\
\int_{I_{j}} \partial_{t} \bigg( \frac{1}{2} u_{h}^{2} \bigg) \,dx &+ \bigg [ (\widehat{au_{h}}) \, u_{h} - \frac{1}{2} a u_{h}^{2} \bigg] \bigg|_{x_{j}}^{x_{j+1}} =0 \\
\sum\limits_{j=0}^{N-1} \int_{I_{j}} \partial_{t}
\bigg( \frac{1}{2} u_{h}^{2} \bigg) \,dx &+
\sum\limits_{j=0}^{N-1} \bigg [
(\widehat{au_{h}}) \, u_{h} -
\frac{1}{2} a u_{h}^{2} \bigg] \bigg|_{x_{j}}^{x_{j+1}} =0
\end{align*}
Date:2017-03-27
\begin{align*}
\{u_{h}\} & = \frac{1}{2} \big( u_{h}^{-} + u_{h}^{+} \big) \\
[[ u_{h} ]] & = u_{h}^{-} - u_{h}^{+} \\
& = u_{h}^{-} \mathbf{n^{-}} + u_{h}^{+} \mathbf{n^{+}} \\
u_{h}^{\pm}(x_{j})(t) & =
\lim\limits_{\epsilon\rightarrow 0} u_{h}^{\pm}(x_{j} \pm \epsilon)(t)
\end{align*}
\begin{align*}
\{u_{h}\} [[ u_{h} ]] & = \frac{1}{2} \big( u_{h}^{-} + u_{h}^{+} \big) \big( u_{h}^{-} - u_{h}^{+} \big)\\
& = \frac{1}{2} \big( u_{h}^{-2} - u_{h}^{+2} \big) \\
& = \frac{1}{2} [[ u_{h}^2 ]]
\end{align*}
\begin{align*}
& \text{Notation:} \\
&\quad
(\widehat{au_{h}})(x_{j}) (t) =
u_{h}^{-} (x_{j}) (t), \quad \text{if} \quad x_{j} \neq 0
\\
&\quad
\{u_{h}(x_{j})(t)\} = \frac{1}{2} \bigg( u_{h}^{-} (x_{j})(t) + u_{h}^{+} (x_{j})(t) \bigg), \quad \{\,\}=\text{Average}
\\
&\quad
[[ u_{h}(x_{j})(t) ]] = u_{h}^{-} (x_{j})(t) - u_{h}^{+} (x_{j})(t), \quad [[\,]]=\text{Jump}
\end{align*}
\begin{align*}
& \sum\limits_{j=0}^{N-1} \int_{I_{j}} \partial_{t} \bigg( \frac{1}{2} u_{h}^{2} \bigg) \,dx + \sum\limits_{j=1}^{N-1} \bigg [
(\widehat{au_{h}}) [[ u_{h} ]] - \frac{1}{2} a [[ u_{h}^2 ]] \bigg] \\
& + (\widehat{au_{h}}) (1)(t) \big(u_{h}^{-}\big) (1)(t) - (\widehat{au_{h}}) (0)(t) \big(u_{h}^{+}\big) (0)(t) -
\frac{1}{2} a \big(u_{h}^{-}\big)^{2} (1)(t) +
\frac{1}{2} a \big(u_{h}^{+}\big)^{2} (0)(t) =0
\end{align*}
\begin{align*}
\partial_{t} \int_{0}^{1} \frac{1}{2} u^{2} \,dx
&= - \frac{1}{2} a u^{2} \bigg|_{0}^{1} \\
&= - \frac{1}{2} a u^{2} (1) + \frac{1}{2} a u^{2} (0)
\end{align*}
\begin{align*}
\sum\limits_{j=1}^{N-1} \bigg( (\widehat{au_{h}}) [[ u_{h} ]] - \frac{1}{2} a [[ u_{h}^2 ]] \bigg) & = \sum\limits_{j=1}^{N-1} \bigg( (\widehat{au_{h}}) [[ u_{h} ]] - a \{u_{h}\} [[ u_{h} ]] \bigg) \\
&= \sum\limits_{j=1}^{N-1} \bigg( (\widehat{au_{h}}) - a \{u_{h}\}\bigg) [[ u_{h} ]] = \sum\limits_{j=1}^{N-1} C [[ u_{h} ]]^{2} \geq 0
\end{align*}
\begin{align*}
(\widehat{au_{h}}) (x_{j})(t) & = \Bigg\{ \begin{array}{l}
a u_{0}(t), \quad \text{if} \quad x_{j} = 0, \\
a \{u_{h}\} + C [[ u_{h} ]], \quad \text{if} \quad x_{j} \in(0,1), \quad C \geq 0,
\quad C = \frac{1}{2} a \quad \text{Upwinding Scheme} \\
au_{h} (1^{-})(t), \quad \text{if} \quad x_{j} = 1.
\end{array}
\end{align*}
\begin{align*}
&(\widehat{au_{h}}) (1)(t) \big(u_{h}^{-}\big) (1)(t) -
\frac{1}{2} a \big(u_{h}^{-}\big)^{2} (1)(t) = \frac{1}{2} a u^{2} (1)(t) \\
&\Rightarrow \frac{1}{2} a \bigg[ \big(u_{h}^{-}\big)^{2} (1)(t) - 2\frac{1}{a} (\widehat{au_{h}}) (1)(t) \big(u_{h}^{-}\big) (1)(t) + u^{2} (1)(t) \bigg ] \\
&= \frac{1}{2} a \bigg[ u_{h}^{-} (1)(t) -u (1)(t) \bigg ]^{2} \geq 0, \\
&\text{while }(\widehat{au_{h}}) (1)(t) = au_{h}^{-} (1)(t)
\end{align*}
\begin{align*}
&(\widehat{au_{h}}) (0)(t) \big(u_{h}^{+}\big) (0)(t) -
\frac{1}{2} a \big(u_{h}^{+}\big)^{2} (0)(t) = \frac{1}{2} a u^{2} (0)(t) \\
&\Rightarrow \frac{1}{2} a \bigg[ \big(u_{h}^{+}\big)^{2} (0)(t) - 2\frac{1}{a} (\widehat{au_{h}}) (0)(t) \big(u_{h}^{+}\big) (0)(t) + u^{2} (0)(t) \bigg ] \\
&= \frac{1}{2} a \bigg[ u_{h}^{+} (0)(t) -u (0)(t) \bigg ]^{2} \geq 0, \\
&\text{while }(\widehat{au_{h}}) (0)(t) = a u_{0}(t)
\end{align*}
---------------------------------
Date:2017-04-10
On, $I_{j} = [ x_{j}, x_{j+1} ]$
\begin{align*}
\int_{I_{j}} (u_{h})_{t} v \,dx &-
\int_{I_{j}} (a u_{h}) v_{x} \,dx +
(\widehat{au_{h}}) \, v \bigg|_{x_{j}}^{x_{j+1}} =0 \\
\text{Take} \quad v(x) \bigg|_{I_{j}} & =
\varphi_{row}^{j}(x) \\
u_{h}(x,t) \bigg|_{I_{j}} & =
\sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \varphi_{col}^{j}(x) \\
\int_{I_{j}} \partial_{t} \bigg( \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \varphi_{col}^{j}(x) \bigg) \varphi_{row}^{j}(x) \,dx &-
\int_{I_{j}} (a \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \varphi_{col}^{j}(x)) \partial_{x} \varphi_{row}^{j}(x) \,dx \\
&+
(\widehat{au_{h}}) \,
\varphi_{row}^{j}(x) \bigg|_{x_{j}}^{x_{j+1}} =0 \\
\Rightarrow \partial_{x} v(x) \bigg|_{I_{j}} & =
\varphi_{row}^{j\,\prime}(x) \\
\partial_{t} u_{h}(x,t) \bigg|_{I_{j}} & =
\sum\limits_{col=0}^{k} \alpha_{col}^{j\,\prime}(t) \varphi_{col}^{j}(x) \\
\int_{I_{j}} \sum\limits_{col=0}^{k} \alpha_{col}^{j\,\prime}(t) \varphi_{col}^{j}(x) \varphi_{row}^{j}(x) \,dx &-
\int_{I_{j}} (a \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \varphi_{col}^{j}(x)) \varphi_{row}^{j\,\prime}(x) \,dx \\
&+
(\widehat{au_{h}}) \,
\varphi_{row}^{j}(x) \bigg|_{x_{j}}^{x_{j+1}} =0
\end{align*}
\begin{align*}
(\widehat{au_{h}}) (x_{j})(t) & = \Bigg \{
\begin{array}{l}
a u_{0}(t), \quad \text{if} \quad x_{j} = 0, \\
a \{u_{h}\} + C [[ u_{h} ]], \quad \text{if} \quad x_{j} \in(0,1), \quad C \geq 0,
\\
a u_{h} (1^{-})(t), \quad \text{if} \quad x_{j} = 1.
\end{array} \\
\quad C = \frac{1}{2} a \quad \text{Upwinding Scheme} \\
(\widehat{au_{h}}) (x_{j})(t)
\bigg |_{C = \frac{1}{2} a }
& = a \{u_{h}\} + \frac{1}{2} a [[ u_{h} ]] \\
& = \frac{1}{2} a \bigg( u_{h} (x_{j}^{-})(t) + u_{h} (x_{j}^{+})(t) \bigg) + \frac{1}{2} a \bigg( u_{h} (x_{j}^{-})(t) - u_{h} (x_{j}^{+})(t) \bigg) \\
& = a u_{h} (x_{j}^{-})(t)
\end{align*}
\begin{align*}
\sum\limits_{col=0}^{k} \alpha_{col}^{j\,\prime}(t) \int_{I_{j}} \varphi_{col}^{j}(x) \varphi_{row}^{j}(x) \,dx
& - a \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \int_{I_{j}} \varphi_{col}^{j}(x) \varphi_{row}^{j\,\prime}(x) \,dx \\
& + (\widehat{au_{h}}) (x_{j+1})(t) \varphi_{row}^{j}(x_{j+1}) - (\widehat{au_{h}}) (x_{j})(t) \varphi_{row}^{j}(x_{j}) =0 \\
\Rightarrow
\sum\limits_{col=0}^{k} \alpha_{col}^{j\,\prime}(t) \int_{I_{j}} \varphi_{col}^{j}(x) \varphi_{row}^{j}(x) \,dx & - a \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \int_{I_{j}} \varphi_{col}^{j}(x) \varphi_{row}^{j\,\prime}(x) \,dx \\
& + a u_{h} (x_{j+1}^{-})(t) \varphi_{row}^{j}(x_{j+1}) - a u_{h} (x_{j}^{-})(t) \varphi_{row}^{j}(x_{j}) =0 \\
\Rightarrow
\sum\limits_{col=0}^{k} \alpha_{col}^{j\,\prime}(t) \int_{I_{j}} \varphi_{col}^{j}(x) \varphi_{row}^{j}(x) \,dx
& - a \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \int_{I_{j}} \varphi_{col}^{j}(x) \varphi_{row}^{j\,\prime}(x) \,dx \\
& + a \sum\limits_{col=0}^{k} \alpha_{col}^{j}(t) \varphi_{col}^{j} (x_{j+1}^{-}) \varphi_{row}^{j}(x_{j+1}) \\
& - a \sum\limits_{col=0}^{k} \alpha_{col}^{j-1}(t) \varphi_{col}^{j-1} (x_{j}^{-})
\varphi_{row}^{j}(x_{j}) =0 \\
\end{align*}
\begin{align*}
\bigg[ \int_{I_{j}} \varphi_{row}^{j}(x) \varphi_{col}^{j}(x) \,dx \bigg]
\bigg[ \alpha_{col}^{j\,\prime}(t) \bigg]
& - a
\bigg[ \int_{I_{j}} \varphi_{row}^{j\,\prime}(x) \varphi_{col}^{j}(x) \,dx \bigg]
\bigg[ \alpha_{col}^{j}(t) \bigg] \\
& + a
\bigg[ \varphi_{row}^{j}(x_{j+1}) \varphi_{col}^{j}(x_{j+1}^{-}) \bigg]
\bigg[ \alpha_{col}^{j}(t) \bigg]
= a
\bigg[ \varphi_{row}^{j}(x_{j}) \varphi_{col}^{j-1}(x_{j}^{-}) \bigg]
\bigg[ \alpha_{col}^{j-1}(t) \bigg] \\
\bigg[ p_{row\,col} \bigg]
\bigg[ \alpha_{col}^{j\,\prime}(t) \bigg]
& - a
\bigg[ q_{1\,row\,col} \bigg]
\bigg[ \alpha_{col}^{j}(t) \bigg] \\
& + a
\bigg[ q_{2\,row\,col} \bigg]
\bigg[ \alpha_{col}^{j}(t) \bigg]
= a
\bigg[ r_{row\,col} \bigg]
\bigg[ \alpha_{col}^{j-1}(t) \bigg]
\end{align*}
\begin{align*}
p_{row\,col} &= \bigg[ \int_{I_{j}} \varphi_{row}^{j}(x) \varphi_{col}^{j}(x) \,dx \bigg] \\
q_{1\,row\,col} &= \bigg[ \int_{I_{j}}
\varphi_{row}^{j\,\prime}(x) \varphi_{col}^{j}(x) \,dx \bigg] \\
q_{2\,row\,col} &= \bigg[ \varphi_{row}^{j}(x_{j+1})
\varphi_{col}^{j}(x_{j+1}^{-}) \bigg] \\
r_{row\,col} &= \bigg[ \varphi_{row}^{j}(x_{j})
\varphi_{col}^{j-1}(x_{j}^{-}) \bigg]
\end{align*}
\begin{align*}
\big[ \mathbf{P} \big] \frac{d}{dt} \big[ \alpha^{j}(t) \big] - a \big[ \mathbf{Q_{1}} \big] \big[ \alpha^{j}(t) \big] + a \big[ \mathbf{Q_{2}} \big] \big[ \alpha^{j}(t) \big]
&= a \big[ \mathbf{R} \big] \big[ \alpha^{j-1}(t) \big]
\end{align*}
---------------------------------
\begin{align*}
\varphi_{col}^{j}(x) &= P_{col} \bigg( s^{j}(x) \bigg) = P_{col} \bigg( \frac{2x-x_{j+1}-x_{j}}{x_{j+1}-x_{j}}\bigg) \\
P_{col} & \text{ : $col^{th}$ degree Legendre Polynomial} \\
s^{j}(x) &= \frac{2x-x_{j+1}-x_{j}}{x_{j+1}-x_{j}}
\end{align*}
----------------------------
\begin{align*}
\frac{d}{dt} u(t) &= f(u,t). \quad \text{Runge Kutta One Step} \\
u_{t} &+ \big[ \mathbf{M} \big] u_{x} = 0 \\
u_{t} &+ \big[ \mathbf{R} \big] \mathbf{\Lambda} \big[ \mathbf{R} \big]^{-1} u_{x} = 0,
\quad \mathbf{\Lambda} = \mathbf{\Lambda}^{+} + \mathbf{\Lambda}^{-}\\
\big[ \mathbf{R} \big]^{-1} u_{t} &+ \mathbf{\Lambda} \big[ \mathbf{R} \big]^{-1} u_{x} = 0 \\
(\big[ \mathbf{R} \big]^{-1} u)_{t} &+ \mathbf{\Lambda}
(\big[ \mathbf{R} \big]^{-1} u)_{x} = 0 \\
(w_{j})_{t} &+ \lambda_{j} (w_{j})_{x} = 0 \\
u_{t} &+ a u_{x} = 0, \quad a > 0 \\
\end{align*}
-----------------------------------------------
\begin{align*}
\big[ \mathbf{P} \big] \frac{d}{dt} \big[ \alpha^{j}(t^{n}) \big] - \big[ \mathbf{A} \big] \big[ \alpha^{j}(t^{n}) \big] + \big[ \mathbf{Q} \big] \big[ \alpha^{j}(t^{n}) \big]
&= \big[ \mathbf{R} \big] \big[ \alpha^{j-1}(t^{n}) \big], \quad \text{O.D.E Runge Kutta One Step} \\
\end{align*}
\begin{align*}
\text{Recall One Step}, \quad t^{n} &\rightarrow t^{n+1} \\
\frac{d}{dt} u(t) &= f(u,t)\\
\text{Multi Step}, \quad t^{n-r}, &\dots, t^{n-1}, t^{n}, \rightarrow t^{n+1} \\
\text{Runge Kutta Method} & \text{: Combination of Forward Euler Method}
\end{align*}
\begin{align*}
\big[ \mathbf{P} \big] \frac{ \big[ \alpha^{j}(t^{n+1}) \big] - \big[ \alpha^{j}(t^{n}) \big] }{\Delta t} -
\big[ \mathbf{A} \big] \big[ \alpha^{j}(t^{n}) \big] +
\big[ \mathbf{Q} \big] \big[ \alpha^{j}(t^{n}) \big]
= \big[ \mathbf{R} \big] \big[ \alpha^{j-1}(t^{n}) \big]
\end{align*}
\begin{align*}
\big[ \alpha^{j}(t^{n+1}) \big] = \big[ \alpha^{j}(t^{n}) \big] + \Delta t \big[ \mathbf{P} \big]^{-1} \bigg(
\big[ \mathbf{A} \big] \big[ \alpha^{j}(t^{n}) \big] -
\big[ \mathbf{Q} \big] \big[ \alpha^{j}(t^{n}) \big] +
\big[ \mathbf{R} \big] \big[ \alpha^{j-1}(t^{n}) \big] \bigg).
\end{align*}
\begin{align*}
\text{In short}, \big[ \alpha^{j,n+1} \big] = \big[ \alpha^{j,n} \big] + \Delta t \big[ \mathbf{P} \big]^{-1} \bigg(
\big[ \mathbf{A} \big] \big[ \alpha^{j,n} \big] -
\big[ \mathbf{Q} \big] \big[ \alpha^{j,n} \big] +
\big[ \mathbf{R} \big] \big[ \alpha^{j-1,n} \big] \bigg).
\end{align*}
\begin{align*}
\Delta t = ?& \quad \text{for CFL Condition} \\
CFL_{L^{2}} & = \frac{1}{2k+1}
\text{, where $k^{th}$ degree Legendre Polynomial} \\
\end{align*}
-----------------------------------------
```
u_t(1,:)=( (A*u_alt(1,:)' - sum(u_alt(1,1:k1_LP)) + sum(u_alt(Nx,1:k1_LP)) * c')' .* b);
for i=2:Nx
u_t(i,:)=( (A*u_alt(i,:)' - sum(u_alt(i,1:k1_LP)) + sum(u_alt(i-1,1:k1_LP)) * c')' .* b);
end
```
```
u_t(1,:)=( ( A*u_alt(1,:)' - Q*u_alt(1,:)' + R * u_alt( Nx,:)' )' .* b);
for i=2:Nx
u_t(i,:)=( ( A*u_alt(i,:)' - Q*u_alt(i,:)' + R * u_alt(i-1,:)' )' .* b);
end
```
### Runge-Kutta Method
在這個筆記中，我們考慮的作法是先把PDE中對空間變數偏微分的部分離散化，整個問題會成為一個微分方程系統方程式
$$
\frac{du}{dt}=f(t,u)
$$
接著我們再使用數值微方的技巧(one-step or multi-step methods)對此系統求解。這個作法我們一般稱為Method of lines或是Semi-discrete Methods。
一般常用的方法是Runge Kutta方法，以下是一種常用的RK3
\begin{eqnarray}
u^{n+1}&=&u^n+\frac{1}{4}(k_1+3k_3) \Delta t\\
k_1 &=& f(t^n,u^n)\\
k_2 &=& f(t^n+\frac{1}{3}\Delta t,u^n+\frac{1}{3}\Delta t k_1)\\
k_3 &=& f(t^n+\frac{2}{3}\Delta t,u^n+\frac{2}{3}\Delta t k_1)\\
\end{eqnarray}
不過在數值偏微分方程中，我們習慣的寫法是
### Homework 2
### 週期性邊界條件
使用提供的範例程式([dg_advection.zip](http://math.ncku.edu.tw/~mhchen/DG/dg_advection.zip))對advection eq
\begin{eqnarray}
u_t +a u_x &=&0, \quad 0\leq x\leq 1, \quad 0\leq t\leq 1\\
u(0,t)&=&u(1,t),\quad 0\leq t\leq 1\\
u(x,0)&=& f(x).\\
a &=& 1,
\end{eqnarray}
$$
f(x) = \left\{
\begin{array}{ll}
(x-0.4)^{10} (x-0.6)^{10} 10^{20}, & \textrm{if } 0.4\leq x \leq 0.6\\
0& \textrm{otherwise}.
\end{array}
\right.
$$
討論以下問題
* 穩定性條件:(CFL number)
* 收斂性*
### Initial-Boundary Value problem
修改提供的範例程式改針對Initial-Boundary Value problem求解
\begin{eqnarray}
u_t +a u_x &=&0, \quad 0\leq x\leq 1, \quad 0\leq t\leq 1\\
u(0,t)&=&0,\quad 0\leq t\leq 1\\
u(x,0)&=& f(x).\\
a &=& 1,
\end{eqnarray}
$$
f(x) = \left\{
\begin{array}{ll}
(x-0.4)^{10} (x-0.6)^{10} 10^{20}, & \textrm{if } 0.4\leq x \leq 0.6\\
0& \textrm{otherwise}.
\end{array}
\right.
$$
```
u_t(i,:)=( (A'*u_alt(i,:)' - sum(u_alt(i,1:pp)) + sum(u_alt(i-1,1:pp)) * c')' .* b);
```
* [Hw2_DG_advection_SSPRK.zip](https://www.dropbox.com/s/2ia6ie3a5wwz5yz/Hw2_DG_advection_SSPRK.zip?dl=0)
* [HighOrderDGforMaxwell.pdf](http://math.ncku.edu.tw/~mhchen/DG/HighOrderDGforMaxwell.pdf)
* [matlab.zip](http://math.ncku.edu.tw/~mhchen/DG/matlab.zip)
* [dg_SSPRK_uv_pbc.m](http://math.ncku.edu.tw/~mhchen/DG/dg_SSPRK_uv_pbc.m)
### Homework 3
### 公式推導
考慮以下一維波方程
\begin{eqnarray}
\frac{1}{c^2} \frac{\partial u}{\partial t} - \frac{\partial v}{\partial x} &=& 0, \quad (0,T)\times (-a,a)\\
\frac{\partial v}{\partial t} - \frac{\partial u}{\partial x} &=& 0, \quad (0,T)\times (-a,a)\\
u(x,t=0)&=& \phi(x), \\
v(x,t=0)&=&-\phi(x), \\
u+cv&=&0 \quad at \, x=a, \\
u-cv&=& 0 \quad at \, x=-a \\
c&=&1, \textrm{ at x=a,-a}
\end{eqnarray}
$$
\phi(x) = \left\{
\begin{array}{ll}
(x-0.4)^{10} (x-0.6)^{10} 10^{20}, & \textrm{if } 0.4\leq x \leq 0.6\\
0& \textrm{otherwise}.
\end{array}
\right.
$$
* (基本)推導DG方法(請手寫或打成pdf檔繳交)
* 推導數值通量(Numerical Flux)
* 穩定性分析
* (基本)數值模擬驗證收斂性
* (進階)考慮有介面的情形
#### 參考解
* [Hw3_DG_SSPRK_wave_uq.pdf](https://www.dropbox.com/s/pu3jswgcjqh9vta/Hw3_DG_SSPRK_wave_uq.pdf?dl=0)
* [Hw3_DG_SSPRK_uq_pbc_v2.m](https://www.dropbox.com/s/ql51q1dexww93j5/Hw3_DG_SSPRK_uq_pbc_v2.m?dl=0)
---
## HW4: Final HW
* [DG2D.pdf](http://math.ncku.edu.tw/~mhchen/DG/DG2D/DG2D.pdf)
* [Notation.pdf](http://math.ncku.edu.tw/~mhchen/DG/DG2D/Notation.pdf)
* [2D_scalar.zip](http://math.ncku.edu.tw/~mhchen/DG/DG2D/2D_scalar.zip)
* * [Note.pdf](http://math.ncku.edu.tw/~mhchen/DG/DG2D/Note.pdf): 推導過程
了解提供演算法以及程式架構後，請修改程式：
* (基本)將初始條件改為類似二維高斯分佈的函數圖形，測試收斂情形。
* (進階)修改程式模擬二維波方程
---
## Elliptic Problems
* [LDG_EIP.zip](http://math.ncku.edu.tw/~mhchen/DG/LDG_EIP.zip): DG Code for Elliptic Interface Problem
* [EIP_mhchen_tjmv4.pdf](http://math.ncku.edu.tw/~mhchen/DG/EIP_mhchen_tjmv4.pdf)
---
* [LectureNotesByCockburn.pdf](http://math.ncku.edu.tw/~mhchen/DG/LectureNotesByCockburn.pdf)
---
Sign in with Wallet
Connect another wallet