# 在計算機裡頭實踐演算法
###### tags: `sysprog`
:::info
主講人: [jserv](http://wiki.csie.ncku.edu.tw/User/jserv) / 課程討論區: [2016 年系統軟體課程](https://www.facebook.com/groups/system.software2016/)
:mega: 返回「[進階電腦系統理論與實作](http://wiki.csie.ncku.edu.tw/sysprog/schedule)」課程進度表
:::
「真正的發現之旅不在於尋求新的風景,而是在於擁有新的眼光。」
> “The real voyage of discovery consists not in seeking new landscapes, but in having new eyes.”
― 法國作家 Marcel Proust
# 21 世紀的變革
[ [source](https://www.facebook.com/shihhaohung/posts/1301538069888678) ]
* 1990 年代中期,大型 NUMA 平行計算系統架構曾發展極盛,但軟體的成熟度與研發速度跟不上系統挾摩爾定律前進的速度,剛好 x86 架構 PC 的效能、Linux 作業系統的泛用性也逼近當時的專業工作站、伺服器,而且二者相乘之後以價廉物美、超多人在用的優勢,讓 HPC 和 datacenter 的趨勢由 NUMA 轉為用許多廉價 PC 等級的機器相串聯而成的 cluster-based 大型系統。
* 事隔 20 年,NUMA 是否會再度興起呢?我認為在那些需要對 big data(或是過程中會產生big data)快速即時做錯綜複雜(交叉)分析的高價值應用而言,NUMA 是達到最高成就的必然之路。只是說,NUMA 其中的 processor-memory interconnect 以及 memory access protocol,比 20 年前有更多樣化的選擇;所謂的 shared memory 系統的定義,也可放寬,例如用 RDMA;而且 GPU、Vector、FPGA 等加速器也應該被涵蓋進來,這和我們探討過的 HSA 相關。
# 利用歐幾里得法 (也就是「輾轉相除法」) 找 GCD
(最大公因數; _Greatest Common Divisor_)
演算法:
1. 大數 := 大數 - 小數
2. 若「最大」和「最小」兩數相同,那麼它就是最大公因數,否則,回到第 1 步
示範:
GCD(48, 40)
```
48 - 40, 40 -> 8, 40
8 != 40, 於是重複上述動作: 40 - 8, 8 -> 32, 8
8 != 32, 於是重複上述動作: 32 - 8, 8 -> 24, 8
8 != 24, 於是重複上述動作: 24 - 8, 8 -> 16, 8
8 != 16, 於是重複上述動作: 16 - 8, 8 -> 8, 8
8 == 8 成立,於是 8 為 GCD
```
用 C 語言實現歐幾里得法: (v1)
```clike=
int findGCD(int a, int b) {
while (1) {
if (a > b) a -= b;
else if (a < b) b -= a;
else return a;
}
}
```
以 Intel C compiler 產生的機械碼來說: (Pentium 4)
|指令|數量|延遲|cycle count|
|:---:|:---:|:---:|:----:|
|減法|5 |1 |5 |
|比較|5 |1 |5 |
|分支|14 |1 |14 |
|其他|0 |1 |0 |
| | | |24 |
改成 mod 操作的 C 語言程式如下: (v2)
```clike=
int findGCD(int a, int b) {
while (1) {
a %= b;
if (a == 0) return b;
if (a == 1) return 1;
b %= a;
if (b == 0) return a;
if (b == 1) return 1;
}
}
```
以 Intel C compiler 產生的機械碼來說:
|指令 |數量|延遲|cycle count|
|:-----------:|:--:|:--:|:--------:|
|mod (整數除法) |2 |68 |136 |
|比較 |3 |1 |3 |
|分支 |3 |1 |3 |
|其他 |6 |1 |6 |
| | | |148 |
如果可排除整數除法和減法的負擔,得到以下實做: (v3)
```clike=
int findGCD(int a, int b) {
while (1) {
if (a > (b * 4)) {
a %= b;
if (a == 0) return b;
if (a == 1) return 1;
} else if (a >= b) {
a -= b;
if (a == 0) return b;
if (a == 1) return 1;
}
if (b > (a * 4)) {
b %= a;
if (b == 0) return a;
if (b == 1) return 1;
} else if (b >= a) {
b -= a;
if (b == 0) return a;
if (b == 1) return 1;
}
}
}
```
可得到更快的實做:
```
v1: 14.56s
v2: 18.55s
v3: 12.14s
```
* 以上數據出自: [The Software Optimization Cookbook: High Performance Recipes for IA-32 Platforms, 2nd Edition](http://www.amazon.com/The-Software-Optimization-Cookbook-Performance/dp/0976483211)
* 但這是 2004 年的表現,現在的電腦架構呢?
## 在 ARM Cortex-A8 上的實驗
* 實驗人: 張家榮
* 平台:BeagleBone Black (ARMv7-A, 1 GHz)
* 實驗程式碼:[github](https://github.com/JaredCJR/GCD_Efficiency_Compare)
* 採用組合語言撰寫 (GCD 的部份),由於 Cortex-A8 不支援 idiv (要在 ARM Cortex-A15 以上才有),所以 以 ARM 組合語言實做[計算機組織課本上的除法器的空間優化版本](https://coursejared.hackpad.com/ch4_Multiplier-and-Divider-wFnZyFI0E6I)。
* 發現gcc的除法似乎有針對2的倍數做判斷,移位(除法)
* 實做的版本尚未考慮exception
* 這裡有個[參考網站](http://me.henri.net/fp-div.html)列出了exception重點
### 實驗方法
* 圖上一個點,代表GCD (big, small) 中的 big,會尋找比它小的所有正整數(>1)的GCD所需的時間「總和」
* 如果有個 big=9995,那麼會找 9993 組 GCD,small 的範圍從 2 到 9994
* 如: (9995,2), (9995,3), (9995,4),......, (9995,9994)
* **所以big越大,找尋的組數越多,整體趨勢微微上升(從左到右)是正常的**
* 重點是比較各演算法的趨勢
### ARM vs. Thumb instruction
* ARM instruction速度較快
* 直線為curve fitting的結果(時間越低,效能越高)
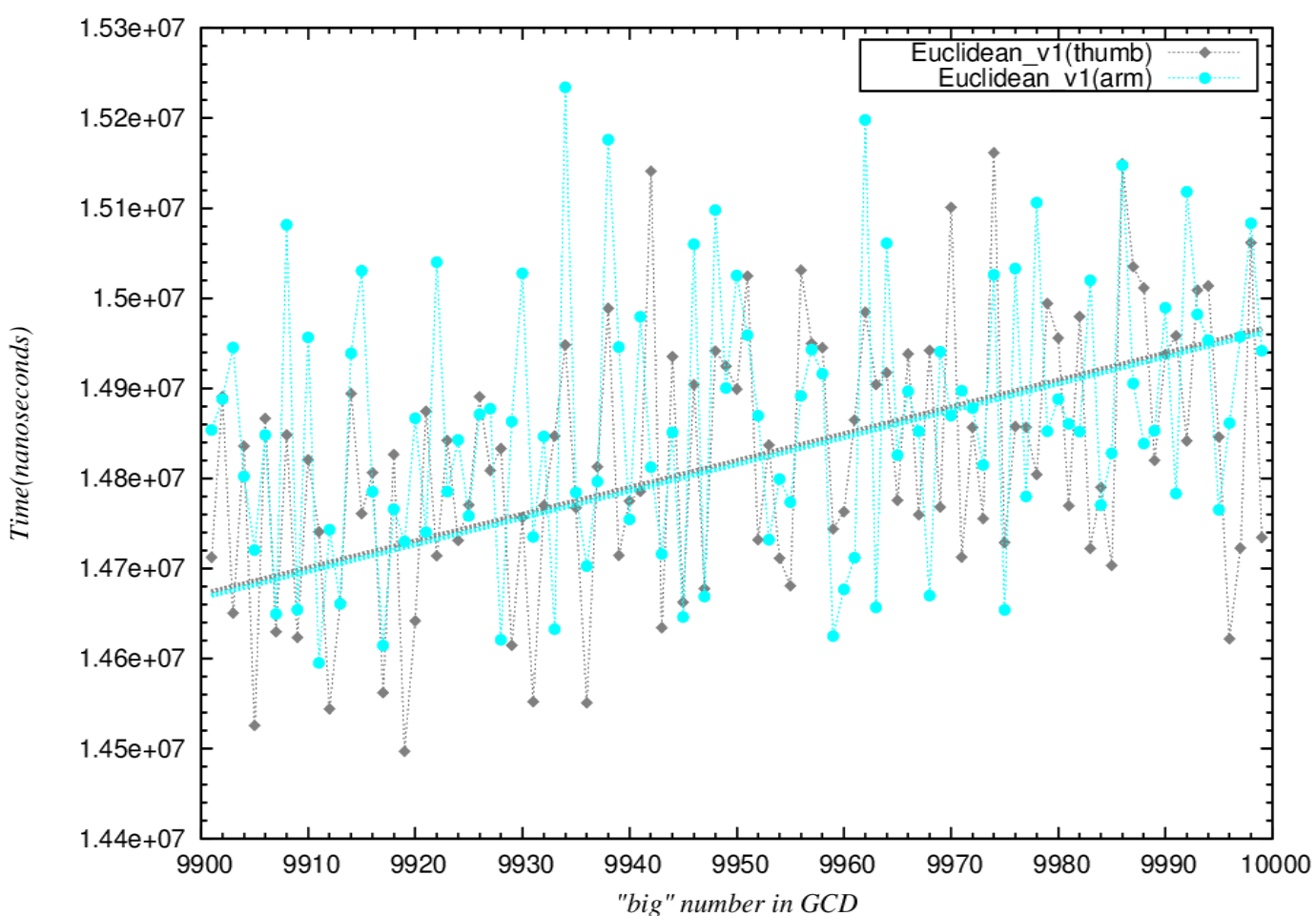
**Assembly**
```
MOD:
@ Entry r0: low (remainder low) must be postive<input:Dividend>
@ r1: high (remainder high) any number
@ r2: Divisor (divisor) must be non-zero and positive<input:Divisor>
low .req r0;
high .req r1;
divisor .req r2;
mov high,#0
.rept 33 @ repeat 33 times
subs high,high,divisor @remainder = remainder - divisor
@it lo
addlo high, high, divisor
adcs low, low, low @ low<<1; ((high-divisor)>0) ? (new bit=1) : (new bit=0)
adc high,high,high @ divisor>>1 == high(64bit for high&low)<<1
.endr
lsr high, #1 @shift remainder to correct position(because last divide don’t know this is the last divide,it still prepare for the next divide<shift>)
@ Exit r0: Quotient (remainder low)
@ r1: remainder (remainder high)
mov pc,lr
```
**Euclidean(thumb) V.S. mod(thumb) V.S. mod_minus(thumb)**
* 不符合預期的原因推估
* v3版本的branch過多(if,else),thumb的branch效能不佳,導致拉低平均
* if數量比較(一個loop)
* v1:3個
* v3:7個

**Euclidean(arm) V.S. mod(arm) V.S. mod_minus(arm)**
* 比較
* 與thumb版本
* arm的branch效能較佳,所以v3版本速度改善最多,這裡符合預期
* v1輸給了v2
* arm的v1與thumb的v1相比,只有微微速度提昇(看第一張圖),但是mod卻提昇較多(幾乎是半張圖片的range),導致了這個結果
* curve fitting

* qemu
* 符合預期

## C語言
* arm-angstrom-linux-gnueabi-gcc內的除法經過最佳化後,效能比減法更佳
.png)
* arm-linux-gnueabihf-gcc(linaro) (without vfpv3)
* 上下圖比較,可以看到整體在arm-angstrom-linux-gnueabi-gcc效能比較好
* 即使在這裡,單純除法比單純減法(的演算法)還快...
* 可是綜合起來看 v3更快(符合預測)

* arm-linux-gnueabihf-gcc(linaro) (with vfpv3)
* mod加快,減法變慢
* 開了比沒開還慢...

## 效能分析: Prefetching
[ [source](https://www.facebook.com/notes/champ-yen/the-power-of-prefetching/1214833498543546) ]
* 論文: "[When Prefetching Works, When It Doesn’t, and Why](http://www.cc.gatech.edu/~hyesoon/lee_taco12.pdf)"
* 用實例顯示 prefetching 帶來的效益,範例是 Matrix Transpose,一個簡單的 C 版本實作如下
```clike=
void naive_transpose(int *src, int *dst, int w, int h)
{
for (int x = 0; x < w; x++){
for (int y = 0; y < h; y++) {
*(dst + x*h + y) = *(src + y * w + x);
}
}
}
```
接著參考 [Programming trivia: 4x4 integer matrix transpose in SSE2](http://www.randombit.net/bitbashing/2009/10/08/integer_matrix_transpose_in_sse2.html) 實作 Intel SSE2 加速的版本,由於先進處理器架構有著 automatic/speculative prefetcher 所以這裡我們故意寫得比較 CPU-unfriendly 一些:
```clike=
void sse_transpose(int *src, int *dst, int w, int h)
{
for (int x = 0; x < w; x += 4) {
for (int y = 0; y < h; y += 4) {
__m128i I0 = _mm_loadu_si128 ((__m128i *)(src + (y + 0) * w + x));
__m128i I1 = _mm_loadu_si128 ((__m128i *)(src + (y + 1) * w + x));
__m128i I2 = _mm_loadu_si128 ((__m128i *)(src + (y + 2) * w + x));
__m128i I3 = _mm_loadu_si128 ((__m128i *)(src + (y + 3) * w + x));
__m128i T0 = _mm_unpacklo_epi32(I0, I1);
__m128i T1 = _mm_unpacklo_epi32(I2, I3);
__m128i T2 = _mm_unpackhi_epi32(I0, I1);
__m128i T3 = _mm_unpackhi_epi32(I2, I3);
I0 = _mm_unpacklo_epi64(T0, T1);
I1 = _mm_unpackhi_epi64(T0, T1);
I2 = _mm_unpacklo_epi64(T2, T3);
I3 = _mm_unpackhi_epi64(T2, T3);
_mm_storeu_si128((__m128i*)(dst+(x*h)+y), I0);
_mm_storeu_si128((__m128i*)(dst+((x+1)*h)+y), I1);
_mm_storeu_si128((__m128i*)(dst+((x+2)*h)+y), I2);
_mm_storeu_si128((__m128i*)(dst+((x+3)*h)+y), I3);
}
}
}
```
我們來撰寫一個使用 SSE prefetch 指令的加速版本:
```clike=
void sse_prefetch_transpose(int *src, int *dst, int w, int h)
{
for (int x = 0; x < w; x += 4) {
for (int y = 0; y < h; y += 4) {
#define** PFDIST 8**
_mm_prefetch(src + (y + PFDIST + 0) * w + x, _MM_HINT_T1);
_mm_prefetch(src + (y + PFDIST + 1) * w + x, _MM_HINT_T1);
_mm_prefetch(src + (y + PFDIST + 2) * w + x, _MM_HINT_T1);
_mm_prefetch(src + (y + PFDIST + 3) * w + x, _MM_HINT_T1);
__m128i I0 = _mm_loadu_si128 ((__m128i *)(src + (y + 0) * w + x));
__m128i I1 = _mm_loadu_si128 ((__m128i *)(src + (y + 1) * w + x));
__m128i I2 = _mm_loadu_si128 ((__m128i *)(src + (y + 2) * w + x));
__m128i I3 = _mm_loadu_si128 ((__m128i *)(src + (y + 3) * w + x));
__m128i T0 = _mm_unpacklo_epi32(I0, I1);
__m128i T1 = _mm_unpacklo_epi32(I2, I3);
__m128i T2 = _mm_unpackhi_epi32(I0, I1);
__m128i T3 = _mm_unpackhi_epi32(I2, I3);
I0 = _mm_unpacklo_epi64(T0, T1);
I1 = _mm_unpackhi_epi64(T0, T1);
I2 = _mm_unpacklo_epi64(T2, T3);
I3 = _mm_unpackhi_epi64(T2, T3);
_mm_storeu_si128((__m128i*)(dst + ((x + 0) * h) + y), I0);
_mm_storeu_si128((__m128i*)(dst + ((x + 1) * h) + y), I1);
_mm_storeu_si128((__m128i*)(dst + ((x + 2) * h) + y), I2);
_mm_storeu_si128((__m128i*)(dst + ((x + 3) * h) + y), I3);
}
}
}
```
接著是測試程式:
```clike=
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <sys/time.h>
//for using x86-SSE2 intrinsics you have to include this
#include <xmmintrin.h>
// PUT naive_transpose, sse_transpose, sse_prefetch_transpose HERE
// ...
#define TEST_W 4096
#define TEST_H 4096
int main(void)
{
//verify the result of 4x4 matrix
{
int testin[16] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 };
int testout[16];
for(int y = 0; y < 4; y++){
for(int x = 0; x < 4; x++)
printf(" %2d", testin[y*4+x]);
printf("\n");
}
printf("\n");
sse_transpose(testin, testout, 4, 4);
for(int y = 0; y < 4; y++){
for(int x = 0; x < 4; x++)
printf(" %2d", testout[y*4+x]);
printf("\n");
}
}
{
struct timeval stime, etime;
int *src =(int*)malloc(sizeof(int)*TEST_W*TEST_H);
int *out0 = (int*)malloc(sizeof(int)*TEST_W*TEST_H);
int *out1 = (int*)malloc(sizeof(int)*TEST_W*TEST_H);
int *out2 = (int*)malloc(sizeof(int)*TEST_W*TEST_H);
srand(time(NULL));
for(int y = 0; y < TEST_H; y++){
for(int x = 0; x < TEST_W; x++)
*(src + y*TEST_W + x) = rand();
}
gettimeofday(&stime, NULL);
sse_prefetch_transpose(src, out0, TEST_W, TEST_H);
printf("sse prefetch: %ld us\n", (etime.tv_sec - stime.tv_sec)*1000000 + (etime.tv_usec - stime.tv_usec));
gettimeofday(&stime, NULL);
sse_transpose(src, out1, TEST_W, TEST_H);
gettimeofday(&etime, NULL);
printf("sse: %ld us\n", (etime.tv_sec - stime.tv_sec)*1000000 + (etime.tv_usec - stime.tv_usec));
gettimeofday(&stime, NULL);
naive_transpose(src, out2, TEST_W, TEST_H);
gettimeofday(&etime, NULL);
printf("naive: %ld us\n", (etime.tv_sec - stime.tv_sec)*1000000 + (etime.tv_usec - stime.tv_usec));
free(src);
free(out0);
free(out1);
free(out2);
}
return 0;
}
```
存成 test.c, 並且按照下列方式編譯
$ gcc -msse2 -o test test.c
在 Intel Core i7 3612QM 執行得到下列結果:
```
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
0 4 8 12
1 5 9 13
2 6 10 14
3 7 11 15
sse prefetch: 57782 us
sse: 117184 us
naive: 228870 us
```
儘管現今 CPU 有著強大的 auto-prefetcher,但是並不是所有的演算都有著規律或是線型的記憶體存取模式, 如此透過優化 prefetching 依然是能夠有相當的效能增進.
在 EeePC 900 (Intel Celeron M 900 MHz) 仍有 22% 的效能差異:
```
sse prefetch: 676158 us
sse: 860861 us
naive: 1644733 us
```
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet