HackMD
Programming Small
tags: sysprog
主講人: jserv / 課程討論區: 2017 年系統軟體課程
返回「嵌入式作業系統設計與實作」課程進度表
在小處下功夫，不放棄整體改善的機會
- 快速計算和表達圓周率
- 字串反轉
- 為什麼 C 語言沒有內建 swap 機制?
- 很難作出通用且有效率的 swap 方式
- Swapping in C, C++, and Java
最佳化來自對系統的認知
假設我們有兩個「有號整數」：
#include<stdint.h>
int32_t a, b;
原本涉及到分支的陳述:
if (b < 0) a++;
可更換為沒有分支的版本:
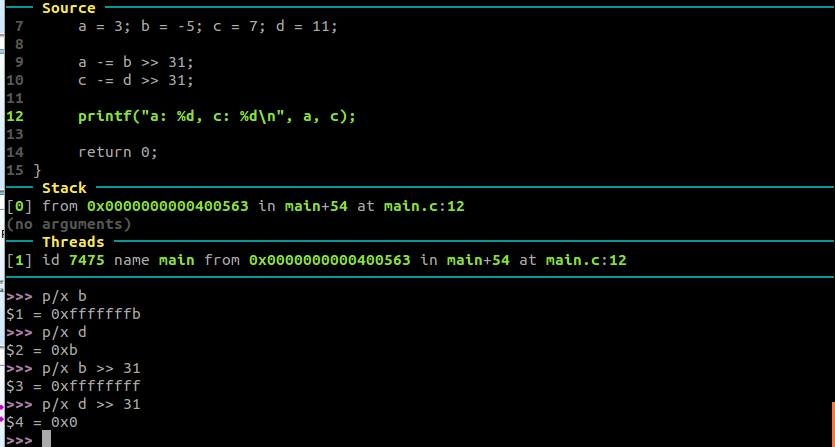
a -= b >> 31;
為什麼呢？一旦 b 右移 31 個 bit，在右移 >> 時在前面補上 sign bit ，所以移完會是 0xffff 也就是-1，故結果會是 a -= -1，即 a++，於是，原本為負數的值就變成 1 ，而原本正數的值就變成 0，又因為原本的行為是有條件的 a++，如此就是數值操作，沒有任何分支指令。
案例分析: Phone Book
目的：分析電話簿搜尋程式，探討 cache miss 對於整體效能有顯著影響
題目說明
思考以下程式碼可能存在的問題，並著手改善效能。
Hint: cache miss
#define MAX_LAST_NAME_SIZE 16
typedef struct __PHONE_BOOK_ENTRY {
char LastName[MAX_LAST_NAME_SIZE];
char FirstName[16];
char email[16];
char phone[10];
char cell[10];
char addr1[16];
char addr2[16];
char city[16];
char state[2];
char zip[5];
struct __PHONE_BOOK_ENTRY *pNext;
} PhoneBook;
PhoneBook *FindName(char Last[], PhoneBook *pHead) {
while (pHead != NULL) {
if (stricmp(Last, pHead->LastName) == 0)
return pHead;
pHead = pHead->pNext;
}
return NULL;
}
- L1 Cache : 32KB = 321024，PhoneBook size = 136 bytes，321024 / (136*8) = 30.12 (只能存 30 筆左右)
- 是否可最佳化成 321024 / (328) = 128 筆？ 或使用 collision 較少的 hash function？
未優化版本
程式碼: phonebook
測試檔：
GitHub上有提供兩種字典檔當輸入 data set，以下測試使用第二種。
- 男生 + 女生英文名字的攻擊(attack)字典檔。約 16,750 個。
- 英文單字表，約 350,000 個 (sorted)
＄ perf stat -r 10 -e cache-misses,cache-references,L1-dcache-load-misses,L1-dcache-store-misses,L1-dcache-prefetch-misses,L1-icache-load-misses ./main_origin
size of entry : 136 bytes
uninvolved is found!
zyxel is found!
whiteshank is found!
odontomous is found!
pungoteague is found!
reweighted is found!
xiphisternal is found!
yakattalo is found!
execution time of append() : 0.053549
execution time of findName() : 0.050462
Performance counter stats for ’./main_origin’ (10 runs):
3,519,048 cache-misses # 96.963 % of all cache refs ( +-1.61% ) [65.55%]
3,629,269 cache-references ( +-1.29% ) [67.73%]
4,185,434 L1-dcache-load-misses ( +-1.10% ) [69.53%]
1,005,501 L1-dcache-store-misses ( +-0.77% ) [70.04%]
3,088,038 L1-dcache-prefetch-misses ( +-1.61% ) [66.24%]
139,497 L1-icache-load-misses ( +-6.17% ) [63.29%]
0.107159363 seconds time elapsed ( +-0.92% )
$ perf record -F 12500 -e cache-misses ./main_origin && perf report
62.36% main_origin libc-2.19.so [.] __strcasecmp_l_avx
16.31% main_origin [kernel.kallsyms] [k] clear_page_c_e
12.87% main_origin main_origin [.] findName
4.54% main_origin [kernel.kallsyms] [k] mem_cgroup_try_charge
0.60% main_origin libc-2.19.so [.] __strcasecmp_avx
0.57% main_origin [kernel.kallsyms] [k] copy_user_enhanced_fast_string
優化版本
程式碼：embedded-summer2015/phonebook (Github)
我的筆電 level 1 cache 有 32 kbit，struct 的大小有 136 bytes，32 * 1024 / (136*8) ＝30.12，若把整個 __PHONE_BOOK_ENTRY 的 struct 都丟進 findName() 尋找，即使未考慮電腦中其他正在運行的程式，我的 level 1 cache 最多也只能放 30 個entry，一共有 35 萬個單字，必定會發生頻繁的 cache miss。
查看電腦 cache 大小 $ lscpu | grep cache
L1d cache: 32K
L1i cache: 32K
L2 cache: 256K
L3 cache: 3072K
第一種優化方式：使用體積較小的 struct
根據題目要求，我們只需要知道「有沒有找到 last name」，對於 email、phone number、address、zip 等等資訊是可以在搜尋過程中忽略不看。另外我又希望能不改變原本 phonebook entry 的結構，所以我另
外設計一個 struct 只儲存 last name，並用一個指向 phonebook entry 的指標叫 detail 來儲存詳細資訊，新的 struct 大小只有 32 bytes，這樣搜尋的過程中，cache 就可以塞進 (32 * 1024) / (328) = 128 個單字，增加 cache hit 的機率。
在實作 appendOptimal() 的過程中，*detail 並沒有沒指向一塊空間，我想專心讓 appendOptimal() 產生含有 lastName 的節點就好。為什麼呢？因為若在 append 過程中 malloc() 空間給 *detail，會增加很多 cache miss，嚴重影響到效能表現，經過實測，總體效能甚至比原始版本還差一點。目前想法是將 *detail 的 assign （當有需要時）交給另外一個 function 處理，畢竟我們一開始只有 last name 的資訊。
typedef struct __LAST_NAME_ENTRY{
char lastName[MAX_LAST_NAME_SIZE];
entry *detail;
struct __LAST_NAME_ENTRY *pNext;
} lastNameEntry;
$ perf stat -r 10 -e cache-misses,cache-references,L1-dcache-load-misses,L1-dcache-store-misses,L1-dcache-prefetch-misses,L1-icache-load-misses ./main_optimal
size of entry : 32 bytes
uninvolved is found!
zyxel is found!
whiteshank is found!
odontomous is found!
pungoteague is found!
reweighted is found!
xiphisternal is found!
yakattalo is found!
execution time of appendOptimal() : 0.044819
execution time of findNameOptimal() : 0.023803
Performance counter stats for ’./main_optimal’ (10 runs):
486,127 cache-misses # 60.472 % of all cache refs ( +- 0.74% ) [65.67%]
803,882 cache-references ( +- 0.37% ) [65.65%]
2,531,398 L1-dcache-load-misses ( +- 1.51% ) [66.70%]
329,753 L1-dcache-store-misses ( +- 1.70% ) [68.36%]
1,642,925 L1-dcache-prefetch-misses ( +- 2.18% ) [69.27%]
100,133 L1-icache-load-misses ( +- 6.45% ) [67.15%]
0.071458929 seconds time elapsed ( +- 0.84% )
$ perf record -F 12500 -e cache-misses ./main_optimal && perf report
36.16% main_optimal [kernel.kallsyms] [k] clear_page_c_e
29.01% main_optimal libc-2.19.so [.] __strcasecmp_l_avx
10.71% main_optimal [kernel.kallsyms] [k] mem_cgroup_try_charge
7.20% main_optimal main_optimal [.] findNameOptimal
4.04% main_optimal [kernel.kallsyms] [k] copy_user_enhanced_fast_string
2.07% main_optimal libc-2.19.so [.] __strcasecmp_avx
1.17% main_optimal [kernel.kallsyms] [k] __rmqueue
第二種優化方式：使用 hash function
第一種方式已經見到不錯的效能成長了！findName() 的 CPU time 從 0.050462 變成0.023803，進步一倍以上。另外 cache miss 的次數從 3,519,048降到 486,127！
不過 35 萬個單字量畢竟還是太大，如果利用字串當作key，對 hash table 作搜尋顯然比每次從頭開始查找快多了。所以接下來的問題就是，如何選擇 hash function？如何減少碰撞發生呢？我選了兩種 hash function。不過以下先用 hash2() 和上面的結果作比較。另外 table size 我使用 42737，挑選的原因是因為有約35萬個英文單字，為了減少碰撞機會，挑了一了蠻大的「質數」。
$ perf stat -r 10 -e cache-misses,cache-references,L1-dcache-load-misses,L1-dcache-store-misses,L1-dcache-prefetch-misses,L1-icache-load-misses ./main_hash
hash table size (prime number) : 42737
size of entry : 32 bytes
uninvolved is found!
zyxel is found!
whiteshank is found!
odontomous is found!
pungoteague is found!
reweighted is found!
xiphisternal is found!
yakattalo is found!
execution time of appendHash() : 0.059560
execution time of findNameHash() :0.000173
Performance counter stats for ’./main_hash’ (10 runs):
367,138 cache-misses #60.950 % of all cache refs ( +- 1.78% ) [61.51%]
602,362 cache-references ( +- 1.62% ) [66.17%]
887,342 L1-dcache-load-misses ( +- 1.20% ) [71.61%]
694,774 L1-dcache-store-misses ( +- 0.92% ) [73.62%]
77,931 L1-dcache-prefetch-misses ( +- 2.12% ) [68.81%]
110,773 L1-icache-load-misses ( +- 8.71% ) [62.00%]
0.061427658 seconds time elapsed ( +- 1.46% )
$ perf record -F 12500 -e cache-misses ./main_hash && perf report
48.01% main_hash [kernel.kallsyms] [k] clear_page_c_e
13.66% main_hash libc-2.19.so [.] _IO_getline_info
12.53% main_hash [kernel.kallsyms] [k] mem_cgroup_try_charge
6.35% main_hash [kernel.kallsyms] [k] copy_user_enhanced_fast_string
1.66% main_hash libc-2.19.so [.] __memcpy_sse2
1.50% main_hash [kernel.kallsyms] [k] __rmqueue
1.36% main_hash libc-2.19.so [.] memchr
1.33% main_hash [kernel.kallsyms] [k] alloc_pages_vma
1.20% main_hash main_hash [.] appendHash
0.97% main_hash [kernel.kallsyms] [k] __alloc_pages_nodemask
執行時間分析
-
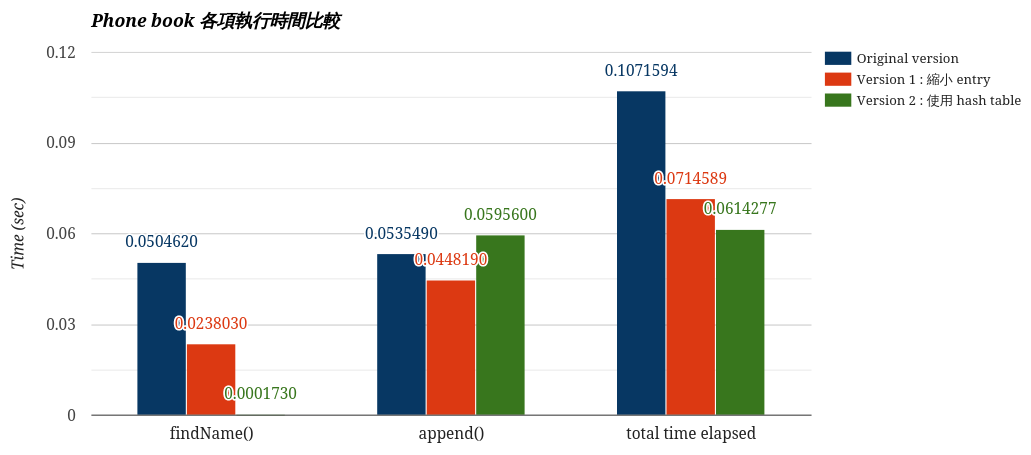
findName()：本次測試需要查找 8 個 last name，兩種優化版本顯然都比原始的還要好，hash 版本不用每次從 35 萬個單字的頭開始找起省掉許多時間，而且再配上縮小過後的 entry，所以 L1 cache 可以塞進更多的 last name，兩種優化方式一加乘，查找時間比原始快了近 300 倍！
-
append()：先來比較 原始版本 和 第一個版本，在 append() 的算法上這兩者幾乎一模一樣唯一的差別就是 malloc() 的記憶體空間不一樣大。
// entry *append(char lastName[], entry *e)
e->pNext = (entry *) malloc(sizeof(entry)); // 136 bytes
// lastNameEntry *appendOptimal(char lastName[], lastNameEntry *lne)
lne->pNext = (lastNameEntry *) malloc(sizeof(lastNameEntry)); // 32 bytes
- 寫個獨立程式來產生 350,000 個 entry，測試這兩者的 page-faults，cache-misses，結果如下。兩者時間相差約 0.0105 sec，和上面 0.00873 sec 差距不大。要動態分配一個大的記憶體空間，它可能產生的效能損失是可觀的。所以如果已知記憶體需求，儘量一開始就分配大塊一點的空間，就如同開學考那題 malloc 2D array 一樣。
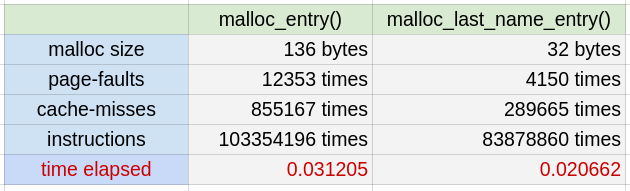
- 最後，同樣都是分配 32 bytes 大小的 entry，hash 版本的 append() 時間，比起第一種版本還多了 0.01474 秒，這是可預期的， 因為為了將 last name 放到對應 bucket，還需要多一步 hash 運算。
cache miss 情形
perf 能偵測的 cache miss 種類非常多，基本上分為 load-miss、store-miss、prefetch-miss 三種，而再根據 cache 種類又分 Level 1 cache 和 Last Level cache，instruction cache 和 data cache，TLB cache。
我們最關心的是L1-dcache-load-misses，也就是要尋找的 data 不在 Level 1 cache，要往更下層的 memory (我的電腦有 L2、L3)。經過縮小 entry後，version 1 的L1-dcache-load-misses減少了 0.4 倍，而 hash 版本則因為查找的數量從 242.6 萬次降到不到 20 次，如下表。進而讓 cache miss 再更減少了近 0.8 倍！不過當然這樣的成果要歸功於一開始辛苦建立 Hash table。
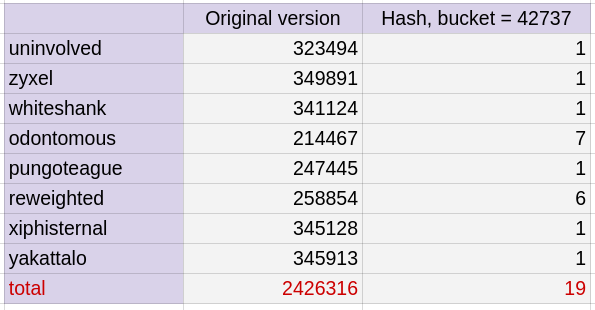
不同 Table size 對效能的影響
Hash function 裡常會對字串作很多次的加法或乘法，以這邊 hash2() 來說除了加法還有乘32，如果我取的不是質數，剛好是某些數字的倍數，譬如 2 或 3 等等，mod 之後就會很容易往某個幾個 bucket 集中，若很不巧我找的字剛好在這幾的 bucket 裡，平均來講效能就不好了，list會很長，所以 table size 我會選用質數。
另外一件事情是， Table size 使用 42737，選用這麼大的數字的考量在 data set 有 35 萬個，size 越大的話，每個 bucket 的 linked list 才不會太長，findName() 起來才會快。
就前面結果我們已經知道 hash 版本速度很快，cache miss 也很低。剩下能主導效能就是查找次數了，以下列出幾個 size 的結果。而當 Table size 大於 7919 時，其查找的次數差異已經非常小了。
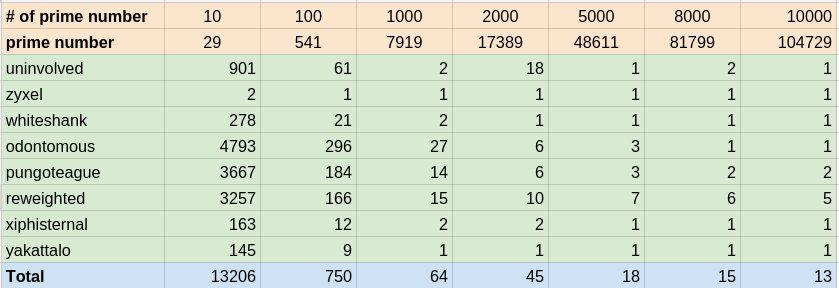
不同的 hash function 對效能的影響
hash2() 是有名的 djb2，兩者差別是 hashVal << 5 ，也就是 hashVal * 32的意思。ASCII 字元的數值最大為 127 的整數，不管是人名還是英文單字當作輸入，平均鍵值長度大約 6～10，所以 hashVal 最多也只有 1270 種可能，不是一個均勻分佈，而在效能表現上可能就有很大的差異。
hashIndex hash1(char *key, hashTable *ht)
{
unsigned int hashVal = 0;
while(*key != ’\0’) {
hashVal+= *key++;
}
return hashVal % ht->tableSize;
}
hashIndex hash2(char *key, hashTable *ht)
{
unsigned int hashVal = 0;
while(*key != ’\0’){
hashVal = (hashVal << 5) + *key++;
}
return hashVal % ht->tableSize;
}
$ ./main_hash with hash1()
hash table size (prime number) : 42737
uninvolved is found! n = 60
zyxel is found! n = 1
whiteshank is found! n = 12
odontomous is found! n = 143
pungoteague is found! n = 192
reweighted is found! n = 133
xiphisternal is found! n = 3
yakattalo is found! n = 8
==> 共 552 次
$ ./main_hash with hash2()
hash table size (prime number) : 42737
size of entry : 32 bytes
uninvolved is found! n = 1
zyxel is found! n = 1
whiteshank is found! n = 1
odontomous is found! n = 7
pungoteague is found! n = 1
reweighted is found! n = 6
xiphisternal is found! n = 1
yakattalo is found! n = 1
==> 共 19 次
Jakub Jelinek 針對不同的 hash function 所作的分析:
The number of collisions in the 537403 symbols is:
name 2sym collision # 3sym collision # more than 3sym collision #
sysv 1749 5
libiberty 42
dcache 37
djb2 29
sdbm 39
djb3 31
rot 337 39 61
sax 34
fnv 40
oat 30
-
應用於 GNU Hash ELF Sections，加速動態函式庫的載入時間
Cache 背景知識
為什麼需要 cache?
電腦發展早期，主記憶體 (main memory) 的速度緩慢且昂貴，CPU 的時脈也不高，但從 1980 年代開始，main memory 和 CPU 的差距急速拉大，主記憶體存取速度雖然時有提升，卻仍不及 CPU 的進展，因此需要 cache 來彌補因為兩者間速度落差帶來的效能衝擊。
-
原理：cache利用Temporal Locality和Spatial Locality設計記憶體架構的兩大原則
-
set associative：set associative的方式，也就是把cache分成多個set，CPU必須檢查指定set內的每個block是否有可用的cache。最極端的情況下就是Fully Associative，也就是CPU要檢查cache內所有的block。
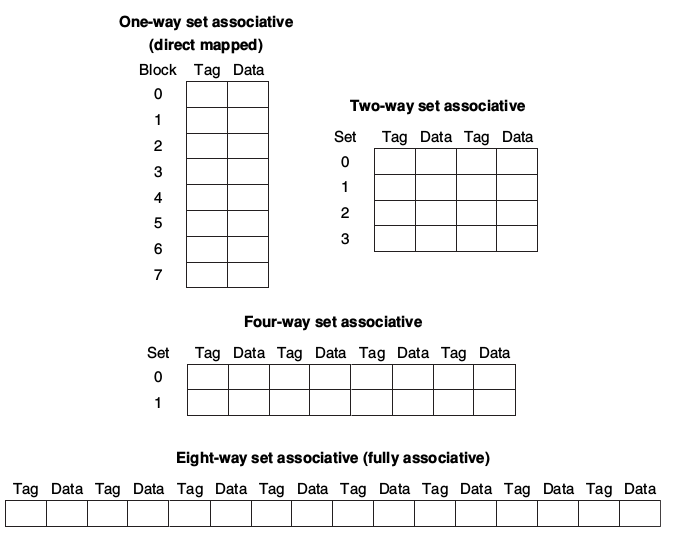
- 實作多個four-way set的方式
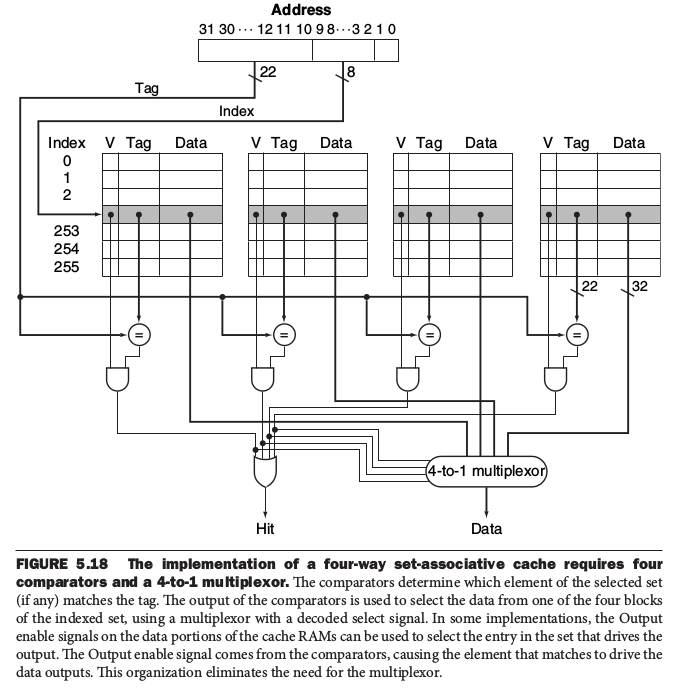
更多內容如下：
-
修改 Makefile，在 CFLAGS 加上
-DNDEBUG，降低 assert() 帶來的影響，重新編譯、執行，再用 perf 分析效能
Hash Function
unsigned int hash(hash_table *hashtable , char *str)
{
unsigned int hash_value = 0;
while(*str)
hash_value = (hash_value << 5) - hash_value + (*str++);
return (hash_value % SIZE);
}
2n - 1 = X << n - X
BKDR hash function
- 特色：計算過程中有seed參與，seed為31 131 1313…
- 出處： 「The C Programming Language"Brian W. Kernighan, Dennis M. Ritchie的 Table Lookup章節
unsigned int BKDRHash(char *str)
{
unsigned int seed = 131;
// 31 131 1313 13131 131313 etc..
unsigned int hash = 0;
while (*str) {
hash = hash * seed + (*str++);
}
return hash;
}
- 為甚麼要乘上一個係數(seed)？
- 若只單純使用各字母的ASCII相加得到hash值，碰撞率很高
- 例如： a(97) + d(100) = b(98) + c(99)
- 所以可以再乘上一個係數，讓hash值差距更大
- 若只單純使用各字母的ASCII相加得到hash值，碰撞率很高
- 為什麼係數(seed)要取 31 131 1313 13131…？
- 把係數分為三種探討： 偶數(2的次方)、偶數(非2的次方)、奇數
- 偶數(2的次方): 取seed=32
- 兩字串：abhijklmn abchijklmn(後者多一個c) 分別帶入上面程式碼，結果為：
- abhijklmn = 3637984782
- abchijklmn = 3637984782
- 兩字串的hash值一模一樣，且把其中一個字串加長為abcdehijklmn，hash值仍沒有改變，為何？
- 計算時若 overflow 變會拋棄最高位，在
hijklmn的前面加上多長的字串，其值仍為3637984782
- 兩字串：abhijklmn abchijklmn(後者多一個c) 分別帶入上面程式碼，結果為：
- 偶數 (非二的次方)
- 可推論其在使用上結果應與上例相同，當結果 overflow 時，就會捨棄最高位，兩字串的 hash 值會相同
- 奇數: 取 seed=31
- 31 = 25-1，即使字串長到會 overflow，但後面的 -1 仍會影響到整體的 hash 值
- 偶數(2的次方): 取seed=32
