# 2016q3 Homework1 (compute-pi)
contributed by <`CheHsuan`>
## 目標
* [作業說明](/s/rJARexQT)
* 學習透過離散微積分求圓周率
* Leibniz formula for π
* 積分計算圓周率π
* Function
* 著手透過 SIMD 指令作效能最佳化
## 程式碼分析
```
__attribute__((unused))
```
在編譯的時候,如果編譯器發現我們有宣告一個變數但從未使用到該變數,則編譯器會發出警告,但此用法是告訴編譯器說,即使未引用到此變數也不要發出warning
:::info
Question : 為什麼編譯器要針對上述情況發出warning?
Answer :
由於如果宣告一個變數便會在process memory space中的data區佔用一個該型態大小的空間,導致剩餘給heap或stack的空間縮小,增加stack overflow的風險
:::
## Performance量測方法
* time指令
<p>
time - run programs and summarize system resource usage
</p>
可以量測另一個指令的實際時間,user space的CPU執行時間和kernel space的CPU執行時間
參考:[Linux 的 time 指令](http://yuanfarn.blogspot.tw/2012/08/linux-time.html)
:::info
Question : 為什麼要分user space和kernel space時間?
Answer :
sys time可以了解整個程式花在ststem call以及kernel對disk IO、network IO和memory allocation所用的時間
user time只是libary call和一般計算所花的時間
:::
## 實作
打算用Leibniz和 Monte Carlo method 等二種方法來求Pi並做比較,而且實作各種加速版本
* multi-thread
* SIMD
## Leibniz formula for π
Leibniz極數求Pi的方法如下表示
>
上述表示式可以縮減成下方公式
>
:::info
Question : 公式怎麼來的?為什麼要除以4?
Anwser :
我們先看一個公式,Gregory's series

那根據高中學到的三角函式,tan(π/4)=1,所以arctan(1)=π/4
將上述的x用1代入,
π/4 = arctan(1)
這樣一來就轉換成
:::
接下來就用C語言來實作看看囉
```C
double compute_pi_leibniz(size_t N)
{
double pi = 0.0;
for(size_t i = 0; i < N; i++) {
double denominator = (2 * i) + 1;
double numerator = pow(-1, i);
pi = pi + (numerator / denominator);
}
return pi * 4.0;
}
```
### Perf分析Leibniz法算PI

效能卡在算-1的N次方上了
### 改進
- [x] 用更簡單的方法算pow(-1, i)
因為只是很規律的1,-1,1,-1,1,......
所以用一個三元運算子就可以取代上述功能
```c
double numerator = (i % 2 == 0 ? 1 : -1);
```
## Monte Carlo method
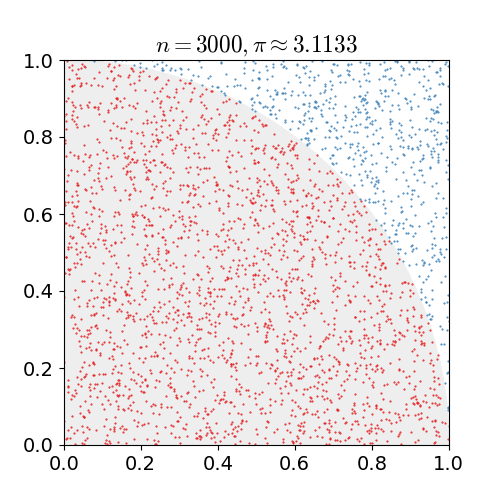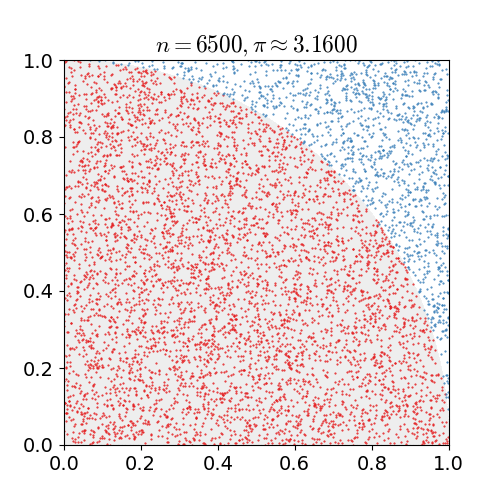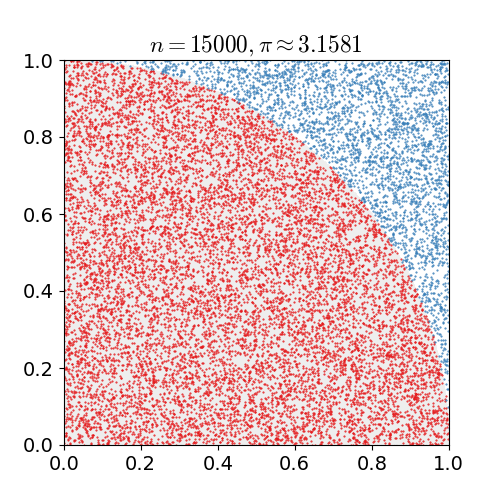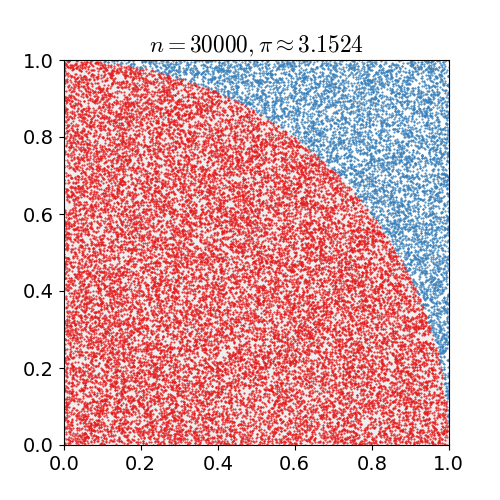
我們從國中就朗朗上口的圓面積公式,πr平方,經由圓面積可以反推算出π,稍後要探討的 Monte Carlo method 就是利用數學統計與機率的方式來解決π計算問題。
### 原理
假設我們有一個圓形的半徑為1,那它的面積即為π,四分之一個圓面積為π/4,利用一個邊長為1的正方形將此四分之一圓包圍起來,在這個正方形範圍內大量產生亂數座標,落在這個四分之一圓的機率應該為趨近於π/4(落在四分之一圓之內和之外的機率和面積成正向關係)
我們可以用下列公式來表示
>π/4 : 1 = S : N
S為落入四分之一圓內座標個數,N為產生亂數次數,轉換一下
>π = 4 * (S / N)
實作看看吧
```C
double compute_pi_montecarlo(size_t N)
{
double pi = 0.0;
size_t sum = 0;
srand(time(NULL));
for (size_t i = 0; i < N; i++) {
double x = (double) rand() / RAND_MAX;
double y = (double) rand() / RAND_MAX;
if ((x * x + y * y) < 1) {
sum++;
}
}
pi = 4 * ((double)sum / N);
return pi;
}
```
這邊補充一下亂數產生的主要兩種方法
1. Hardware random number generator, TRNG
又稱為true random number generator,TRNG最主要是利用現實的一些細微雜訊來產生亂數,比方說環境中熱量的變化、光電效應等不可預測的類比訊號轉換成一連串的0101數位訊號,取樣後即可取得真正的亂數
2. Pseudo random number generator, PRNG
PRNG並不是真正的random,而是會因為初始值經過數學運算後而產生一連串相關的數字,該初始值稱為seed,如果將seed的值固定,每一次產生出來的數值序列都會一樣,所以說在上面的code當中,我們利用時間函數來當作我們的seed,讓之後做benchmark時,不會都跑出一樣的PI
{%youtube itaMNuWLzJo %}
:::info
Question : 什麼數學運算?
Answer :
對於seed的多項式運算,同樣的,下一次產生的亂數值是由這一次所產生的亂數值做多項式運算所產生
:::
### Perf分析 Monte Carlo 法計算 PI
```shell=$
./time_test_montecarlo_pthread & sudo perf top -p $!
```

可以看出來大部份的時間(80%)都花在產生random的座標點位上,應該就是我們的效能瓶頸了
### 改進的方法
- [x] 使用pthread(multi-thread)方式來加速運算
- [x] 使用[cuRAND來平行產生亂數](http://cs.umw.edu/~finlayson/class/fall14/cpsc425/notes/23-cuda-random.html)並用cuda來計算
- [ ] 不要用rand()方法產生亂數?
### 實驗數據
#### 原始版

<center>Leibniz和Monte Carlo</center>
有時使用openMP 4個thread的時間會大於不使用多執行緒的時間,不是很穩定
#### pthread版

<center>Monte Carlo with 4 threads</center>
目前測試結果很奇怪,multi-thread的執行時間大於single thread,目前先把結果放上來,再慢慢debug
:::info
Question : 為什麼multi-thread不會比較快?
先man一下srand和rand看解說
>The function rand() is not reentrant or thread-safe, since it uses hidden state that is modified on each call. This might just be the seed value to be used by the next call, or it might be something more elaborate. In order to get reproducible behavior in a threaded application, this state must be made explicit; this can be done using the reentrant function rand_r().
有兩個關鍵字:==not reentrant== 、==not thread-safe==
裏面有提到如果要保有reentrant的特性,要使用rand_r()
```
int rand_r(unsigned int *seedp);
```
原因是在rand()有用到靜態變數(或全域變數),所以可能因為interrupt或其他thread也運行到rand(),導致該靜態變數或全域變數變得不可預期。而如果使用rand_r()的方式,每次呼叫都會給予新的種子值,並不使用靜態變數(或全域變數)來紀錄上一次所產生的亂數值並且當作下一次產生的基準,因此rand_r()具有reentrant特性
其他例子:strtok()與strtok_r()
參考一下老師提供[資料](http://www.evanjones.ca/random-thread-safe.html)
當我們要multi-thread的環境下要使用非thread-safe時,必須自己加上lock,所以說,我們應該要使用可以傳入state的函式如上述rand_r()
令一個老師給的[討論串](http://stackoverflow.com/questions/2772090/whether-rand-r-is-real-thread-safe)
裏面有提到什麼三種狀況來區別thread-safe
1) Not thread safe at all. It is unsafe to call the function concurrently from multiple threads. For example, strtok.
2) Thread safe with respect to the system. It is safe to call the function concurrently from multiple threads, provided that the different calls operate on different data. For example, rand_r, memcpy.
3) Thread safe with respect to data. It is safe to call the function concurrently from multiple threads, even acting on the same data. For example pthread_mutex_lock.
在JAVA環境中,只有第3種才被定義為真正的thread-safe
最後回答為什麼multi-thread不保證比較快,原因是有使用到pthread_join來讓整體程式等待每個thread都完成運算才能結束,因此如果有某條thread特別慢的話,整體程式的效能也會被拖累。
:::
#### cuda版
最近開始學cuda,想說就拿來應用看看,以下是寫CUDA的基本流程

列出我用的GPU訊息
```
Device 0 Name: GeForce GT 650M
Total global memory: 2147287040
Total shared memory per block: 49152
Total registers per block: 65536
Warp size: 32
Maximum memory pitch: 2147483647
Maximum threads per block: 1024
Maximum dimension 0 of block: 1024
Maximum dimension 1 of block: 1024
Maximum dimension 2 of block: 64
Maximum dimension 0 of grid: 2147483647
Maximum dimension 1 of grid: 65535
Maximum dimension 2 of grid: 65535
Clock rate: 950000
Total constant memory: 65536
Texture alignment: 512
Concurrent copy and execution: Yes
Number of multiprocessors: 2
Kernel execution timeout: Yes
```

用GPU就是猛!
:::info
Question : 為什麼GPU執行時間是常數分佈?
Answer :
因為在GPU的cuRAND使用上,每個thread在使用curand()時,都必須傳入state,這樣一來每個thread間就不需要做同步,因此就在performance上可以有良好的表現
:::

但是使用Monte Carlo算PI的缺點就是error rate的振盪很嚴重,沒有那麼的smooth,雖然還是會收斂,但N愈大不保證error rate會愈小,一切都是機率問題。
在GPU版本中,根據N值不同,我使用到的block數也不同,但每個block內的thread數是固定為500,每一個thread都會跑固定迴圈數,迴圈裡使用cuRAND產生亂數,並且計算在四分之一圓內的點位數。
這樣一來,gpu已經把最繁重的部份解決掉,cpu只要把每個thread算出來的加總再總加總一次算機率就可以了。
接下來的課題就是如何更自動化分配block數量和thread數量和分析帶來的效能影響
## GitHub
https://github.com/CheHsuan/compute-pi
## 參考
[1]cuRAND範例 http://cs.umw.edu/~finlayson/class/fall14/cpsc425/notes/23-cuda-random.html
[2]亂數產生器wiki https://en.wikipedia.org/wiki/Random_number_generation