# 2017q3 Homework1 (ternary)
contributed by <`Feng270`>

- [ ] 解釋 Balanced Ternary 原理

> TODO: 詳細閱讀 [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)，理解 base-3 的原理 (並且複習數位邏輯)，整理 base-3 基礎運算操作
> [name="jserv"][color=red]

---

## 對於上古文字的想法
一開始看到如作業圖中的方塊圖會不知道它在表達什麼，只知道與 3 位元表示法有關，不過多試了幾個範例似乎可以找到一點想法：

┌───┐            ┌───┐
┤   │            ┤   │
└┴┴─┘(5)         └─┬─┘ (10)

只知道凸出爲 + 凹入爲 -，不過試著把 5 跟 10 使用 3 進位組合來表示，得到
$5 = 3^1 + 3^0 + 3^0$ 以及 $10 = 3^2 + 3^0$
10 比較好理解 0 與 2 的邊凸出，但 5 好像不是這麼一回事，有兩個 0 次方的項，因此再改寫爲
$5 = 3^2 - 3^1 - 3^0$
就符合圖中 2 次的邊凸出，而 0 與 1 的邊凹入，因此得到以下原理。

## 原理
Balanced Ternary 能夠使用一個邊長爲 3 單位的正方形來表示數字，從下邊中間爲 3 的 0 次方，依序往左爲 3 的 1 次方到下邊右側爲 3 的 8 次方，而凸出爲加法(或正值)，反之凹入爲負值（或減法），若 0 則不變，以下舉個例子說明，假設我們想表示 `100`，做法如下
1. 首先`100`可表示爲 $3^4 + 3^3 - 3^2 + 3^0$
2. 確定每一次項最多只有一項
3. 畫出每次項所代表邊的凹凸

├─┴─┐
├   │
└─┬─┘(100)

除了圖形的表示法之外，一般使用 `+1,0,-1` 來表示數字，而為了使用上的方便 `-1` 也常使用 `T` 來表示~[1]~，同樣使用 100 來做例子，由以上改寫 3 次方組合可得知 3 的 0~4 次方係數為 +1,+1,-1,0,+1 因此 100 使用 Balanced Ternary 記為 `11T01`，而表示負數也是一樣，-100可以使用 3 次方表示為
$-100 = -(3^4) - 3^3 + 3^2 - 3^0$
可表示為`TT10T`，與 100 相比較就是差一個負號，因此表示負數也是容易的。
## 補完：浮點數的表示法~[1]~
除了整數，Balanced Ternary 是否能夠實作浮點數呢？答案是肯定的，我們可以輕易地將浮點數表示成 3 次方的組合，以 `0.6` 為例：

0.6 => 0.6 * 3 = 3 - 1.2 (取 1)
       -1.2 * 3 = -3 - 0.6 (取 T)
       -0.6 * 3 = -3 + 1.2 (取 T)
       1.2 * 3 = 3 + 0.6 (取 1)
       0.6 * 3 = 3 - 1.2 （取 1）(loop 同第一行結果)

由以上計算可得知 $0.6 = 3^0 - 3^{-1} - 3^{-2} + 3^{-3} + 3^{-4}$...，因此 0.6 可表示為 $1.\overline{TT11}$，但有時也會遇到表示不唯一的問題，這裡舉`0.5`來當做例子：

0.5 => 0.5 * 3 = 0 + 1.5 (取 0)
       1.5 * 3 = 3 + 1.5 (取 1)
       1.5 * 3 = 3 + 1.5 (取 1) (loop 同第二行結果) 

可以寫為：

0.5 => 0.5 * 3 = 3 - 1.5 (取 1)
       -1.5 * 3 = -3 - 1.5 (取 T)
       -1.5 * 3 = -3 - 1.5 (取 T) (loop 同第二行結果)

由上方結果可寫成 $0.\overline{1}$，下方結果寫為 $1.\overline{T}$，若將兩數相加 $0.\overline{1}+1.\overline{T}$ 正好也等於 1，變相的解釋了 0.5 有兩種表示法的原因，我猜這應該也是計算機界後來沒有採用 3 位元運算的原因之一吧XD
> 這個猜測不精確，請考慮到 balanced ternary 加法器的設計來思考。
> 注意：作業要求頁面已更新，追加相關的 YouTube 教學影片，請詳閱並充分記錄
> [name="jserv"][color=red]

> 好的，我會在去研讀相關的知識，謝謝老師
> [name=Feng270]

## 運算~[2]~
> 請閱讀 [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)，關注於 ternary multiplexer, Unary functions, half-adder, Consensus, full adder, Overflow
> [name="jserv][color=blue]
### Multiplexer (多工器)
在開始介紹運算前先來看 Ternary 的 Multipexer，由下圖可知該多工器有 5 支針腳，分別為`inN,inO,inP,sel`以及`out`，而 out 的結果取決於 (inN,inO,inP) 針腳對於 sel 針腳輸入為 (-1,0,1) 的結果，該硬體為運算實作的基本單元。

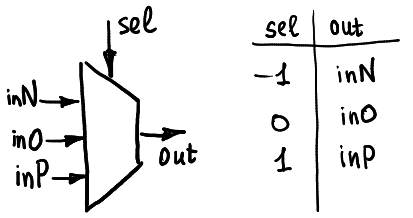
### Unary functions
這裡介紹了四種以上述 Multipexer 制成的 function，分別爲 `A+1,A-1,max(A,0),min(A,0)` 而這些 function 將會成爲以下運算的元件。

### Half-adder
所謂 Half-adder (半加器) 爲輸入只有 A 與 B 兩個參數，而輸出是 Sum 值 (不考慮進位加總後的值)，以及 Carryout 值 (表示進位)，因此分成以下兩部分：
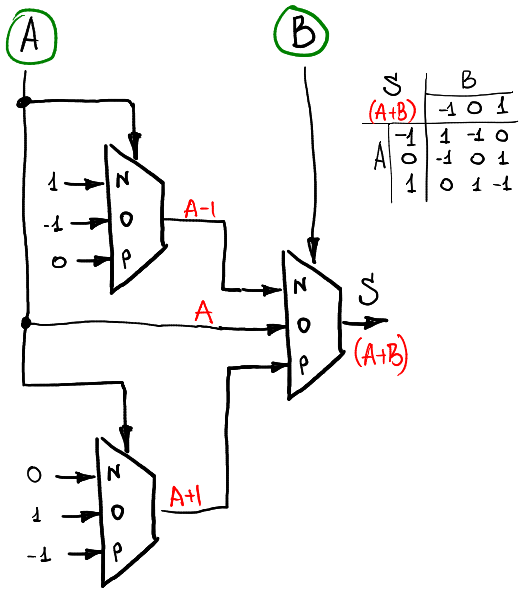
上圖爲不考慮進位問題時的半加器 (只表示 Sum 項)，以左列爲 A，上行爲 B，以下表示 A+B 的真值表，我們可以觀察此表格發現當只有 Sum 值時，Multipexer 的輸入爲 `A-1,A,A+1`。
| Sum | -1 | 0 | 1 |
| - | - | - |-|
| -1 | 1 | -1 | 0 |
| 0 | -1| 0 | 1|
| 1 | 0 | 1 | -1 |

而第二個部分爲 Carryout 值，我們同樣可以使用真值表來反推輸入的 function，一樣以左列爲 A，上行爲 B，可以觀察到，Multipexer 的輸入爲 `min(A,0),0,max(A,0)`。
| Carryout | -1 | 0 | 1 |
| - | - | - |-|
| -1 | -1 | 0 | 0 |
| 0 | 0| 0 | 0|
| 1 | 0 | 0 | 1 |

### Fulladder
有了以上半加器的概念之後，可以試著理解全加器的實作，全加器有 3 個輸入，分別爲 `A,B,Carry-in`，此處的 Carry-in 爲上一位的進位值，而輸出則爲 A+B+C-in，可以拆成 (A+B)+C，因此可得下圖，其中包含了上述的半加器。
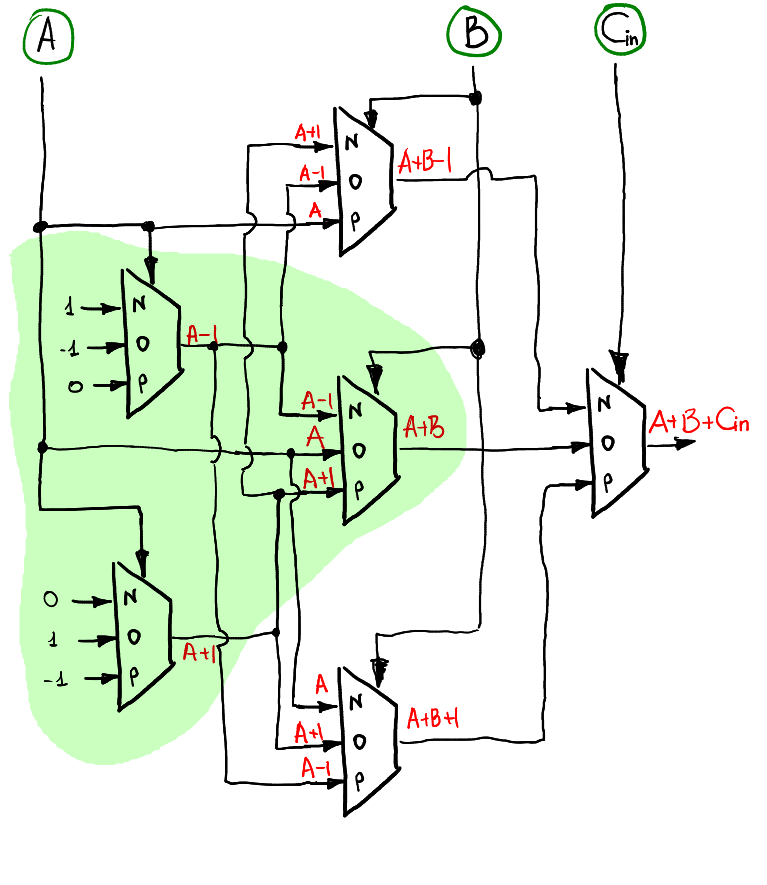
### Overflow
Overflow 則是由半加器第二部分 Carryout 所兜出來的架構。
到此 Ternary 的基本運算就告一段落了。

---

- [ ] Balanced Ternary 的設計要解決什麼類型的問題，需要詳述實際應用案例 (如 IOTA/Tangle)。提示：從算術表達的精準度和空間使用效率去探討;

---

## Balanced Ternary 可以解決的問題：
> TODO: 研讀 [balanced255](https://github.com/lowagner/balanced255)，概念是把 C-style string (用 null terminator 結尾的字串) 轉化為一組數值，並以 `-128` 結束，思考能否帶來更好的空間使用率？
> [name="jserv"][color=red]

## 參考資料
1. [Balanced ternary - Wikipedia](https://en.wikipedia.org/wiki/Balanced_ternary)
2. [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)