# 2018q1 Homework3 (list)
contributed by <`bauuuu1021`>
* [作業說明](https://hackmd.io/s/HkxZbJzif)
## 生日悖論
- [ ] 自我檢查事項
* 如何透過近似的運算式,估算上述機率計算呢?附上有效的 LaTeX 算式
* 參考 [Birthday problem](https://en.wikipedia.org/wiki/Birthday_problem)
* 令 n 人生日不重複機率為 $p(\bar n) = \frac{365}{365}*\frac{364}{365}*\frac{363}{365}*...* \frac{366-n}{365} = 1 * (1-\frac{1}{365})*(1-\frac{2}{365})*(1-\frac{3}{365})*...* (1-\frac{n-1}{365})$( 不考慮 2/29 )
* 引入 [Taylor series](https://en.wikipedia.org/wiki/Taylor_series)
* $e^x = 1+x+ \frac {x^2}{2!}+ \frac {x^3}{3!}+...\approx1+x$ (when x<<1)
* 代回 $p(\bar n)$ = $1*e^\frac {-1}{365}*e^\frac {-2}{365}*e^\frac {-3}{365}*...*e^\frac {-(n-1)}{365}$= $e^\frac {-n(n-1)/2}{365}$ = $e^\frac {-n(n-1)}{730}$
* 因此 n 人中有人生日重複的機率為 $p(n)=1-e^\frac {-n(n-1)}{730}$
* [Birthday problem](https://en.wikipedia.org/wiki/Birthday_problem) 對資訊安全的影響在哪些層面?
* 可能造成 [生日攻擊](https://www.getit01.com/p2017120653854/),即在設計不佳的 hash function 中,可能會導致在極小數量的輸入試驗中便得到相同的輸出值 (collision)。例如:hash(name)=birthday 就是不佳的 hash function。此外,hash function 的演算法太容易在幾組輸入輸出便被猜出,也會被視為不安全的使用。例如:f(x)=x
* 實務上 [MD5](https://en.wikipedia.org/wiki/MD5) 常被用來檢視下載的文件是否被惡意修改或下載時是否出錯,只要文件下載完計算 MD5 再看看 hash 值是否跟官網公佈的相同即可得知。但在一定數量級的嘗試內可能被產生碰撞,如下表

* 例如一個 128 位的 hash function,$2.2*10^{19}$ 次嘗試就有超過 50% 的機率會產生碰撞
* 由於 SATA 硬碟發生 1bit 的傳輸錯誤機率約在 $10^{-15}$ 以下,因此將輸入數值降低到使碰撞機率控制在$10^{-15}$ 以下就可算是理想的。例如 128 位的 hash function 在輸入數量在 $8.2*10^{11}$ 以下可算是理想的。
* 產生碰撞後就有機會透過分析而得知 hash function 的演算法,而讓有心人士再製造一份 hash 值一樣的文件來替換且無法被察覺。
* 像是 [Random Number Generator](http://stattrek.com/statistics/random-number-generator.aspx) 這樣的產生器,是否能產生「夠亂」的亂數呢?
* 連結的 [Random Number Generator](http://stattrek.com/statistics/random-number-generator.aspx) 有個 optional 選項 seed ,發現填入數字前每次產出的亂數都不一樣,但填入後每次產生的亂數表都一樣
* random number generator 可分為 [CSPRNG](https://en.wikipedia.org/wiki/Cryptographically_secure_pseudorandom_number_generator) 及 [PRNG](https://en.wikipedia.org/wiki/Pseudorandom_number_generator) 兩種,後者為 linear congruence generator,意即相鄰兩數為 linear function 之關係。詳見 [參考資料](https://softwareengineering.stackexchange.com/questions/124233/why-is-it-impossible-to-produce-truly-random-numbers?utm_medium=organic&utm_source=google_rich_qa&utm_campaign=google_rich_qa)
* 題目所提供的 Random number generator 無法產生夠亂的亂數,(或應該說:真正的亂數),必須要 **CSPRNG** 才有辦法
* [dieharder](https://github.com/seehuhn/dieharder) 是一個可以檢驗 PRNG 品質的程式
## Linux 風格的 linked list
- [ ] 自我檢查事項:
* 為何 Linux 採用 macro 來實作 linked list?一般的 function call 有何成本?
* 參考 [比較 macro 與 function 的優劣點](http://blog.xuite.net/lukeatnchu/blog/221675116-%E6%AF%94%E8%BC%83+macro+%E8%88%87+function+%E7%9A%84%E5%84%AA%E5%8A%A3%E9%BB%9E),節錄如下:
* macro: 在編譯時就將原本 macro 展開成其所定義的敘述,因此執行時不需跳躍。執行速度快,但如果多次呼叫會佔用許多記憶體空間
* function call: 編譯時不展開,執行時需跳躍到 function 處,因此速度較慢。但如果多次呼叫會節省許多空間
* 因此推測會使用 macro 原因是:
* 犧牲一點空間來讓執行速度加快
* macro 的易讀性高
* 先將一些常用的操作以 macro 定義好,可以省去之後的開發者再自行實作的時間
* Linux 應用 linked list 在哪些場合?舉三個案例並附上對應程式碼,需要解說,以及揣摩對應的考量
* [Linux kernel 排程機制](http://loda.hala01.com/2017/06/linux-kernel.html)
* [linux kernel reading(1)](https://blog.csdn.net/zhongshu_gu/article/details/1731063)
* 在 linux Kernel 2.6 中,每個處理器都有兩個 Task Queue,當 Active Task Queue 中的 task 執行完畢,就會依據 Priority level 及 Time Slice 放到 Expired Task Queue中。當 Active Task Queue 執行完畢後,就 Switch 這兩個 Task Queue,開始執行經過計算後的新Active Task Queue。如下圖:
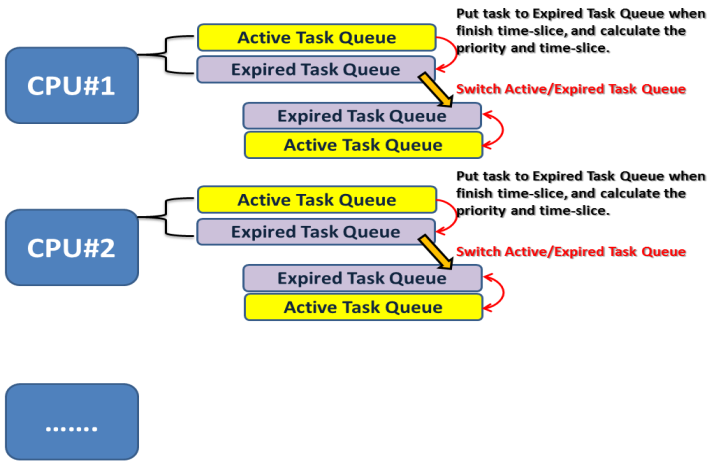
* task_struct 中的 run_list 是以呼叫 list_head 的方式使用 linux 中的 doubly-linked list 把同一個 Task Priority 的行程串起來,對應的程式碼下
```=
struct task_struct {
volatile long state; /* -1 unrunnable, 0 runnable, >0 stopped */
struct thread_info *thread_info;
atomic_t usage;
unsigned long flags; /* per process flags, defined below */
unsigned long ptrace;
int lock_depth; /* Lock depth */
int prio, static_prio;
struct list_head run_list;
………
}
```
* [存](https://isis.poly.edu/kulesh/stuff/src/klist/)
* GNU extension 的 [typeof](https://gcc.gnu.org/onlinedocs/gcc/Typeof.html) 有何作用?在程式碼中扮演什麼角色?
* typeof(x) 會回傳 x 的資料型態
* 在 [typeof 在 kernel 的使用](http://deltamaster.is-programmer.com/posts/37253.html) 有淺顯易懂的例子解說
```=
int a;
typeof(a) b; //即 int b;
typeof(&a) c; //即 int* c;
```
* 在 kernel 中可以這麼使用
```=
/*
* Check at compile time that something is of a particular type.
* Always evaluates to 1 so you may use it easily in comparisons.
*/
#define typecheck(type,x) \
({ type __dummy; \
typeof(x) __dummy2; \
(void)(&__dummy == &__dummy2); \
1; \
})
/*
* Check at compile time that 'function' is a certain type, or is a pointer
* to that type (needs to use typedef for the function type.)
*/
#define typecheck_fn(type,function) \
({ typeof(type) __tmp = function; \
(void)__tmp; \
})
```
* 在 typecheck() 中,如果 x 的資料型態不是 type 的話就會跳出 warning 訊息,因為兩個資料型態的東西使用 == 這個 operator 時會跳出警告
* 在 typecheck_fn() 中,如果 function 的 return type 與參數 type 不相符的話一樣會跳出 warning
>[color=green]TODO:實驗程式
* 解釋以下巨集的原理
```
#define container_of(ptr, type, member) \
__extension__({ const __typeof__(((type *) 0)->member) *__pmember = (ptr); \
(type *) ((char *) __pmember - offsetof(type, member)); \
})
```
* 巨集中 `offsetof()` 的定義如下
```
#define offsetof(TYPE, MEMBER) ((size_t) &((TYPE *)0)->MEMBER)
```
* 根據 [container_of 巨集](http://adrianhuang.blogspot.tw/2010/01/linux-kernel-containerof.html) 中的解釋,這段敘述代表以零為起始位址算出 member 這個成員的相對位址,例如:
```=
#include <stdio.h>
#include <stddef.h>
typedef struct {
char name[16];
int age;
char studentId[12];
} idCard;
int main () {
idCard myData = {"bauuuu1021",21,"f74041145"};
printf("offset of studentId %d\n", offsetof(idCard,studentId)); //output 20
}
```
* container_of() 這個巨集的功能是如果只知道這個結構中某成員的位址,即可透過這個巨集得到結構的起始地址
```=
#include <stdio.h>
#include <stddef.h>
typedef struct {
char name[16];
int age;
char studentId[12];
} idCard;
int main () {
idCard myData = {"bauuuu1021",21,"f74041145"};
printf("addr of stutentId %p\n", &myData.studentId);
printf("offset of studentId %d\n", offsetof(idCard, studentId));
printf("addr of name %p\n", &myData.name);
printf("addr of myData(struct) %p\n", container_of(&myData.studentId,idCard, studentId));
}
```
:::info
不知道為什麼最後一行有錯誤@@
:::
```
container_of.c:15:73: error: expected expression before ‘struct’
printf("addr of myData(struct) %p\n", container_of(&(myData.studentId),struct idCard, studentId));
^
```
>在以上程式碼加上 #define container_of 之定義即可解決問題[name=bauuuu1021][color=red]
* 除了你熟悉的 add 和 delete 操作,`list.h` 還定義一系列操作,為什麼呢?這些有什麼益處?
* 一些 macro 像 INIT_LIST_HEAD() 等固然可以在短短幾行實作完成,但使用 macro 管理讓開發者降低實作的負擔,多人開發時易讀性也較高
* `LIST_POISONING` 這樣的設計有何意義?
* list.h 中的 list_del() 有這段註解及定義
```
/*
...
* LIST_POISONING can be enabled during build-time to provoke an invalid memory
* access when the memory behind the next/prev pointer is used after a list_del.
* This only works on systems which prohibit access to the predefined memory
* addresses.
*/
...
#ifdef LIST_POISONING
node->prev = (struct list_head *) (0x00100100);
node->next = (struct list_head *) (0x00200200);
#endif
```
* 在 list_del() 時,節點不會真的被刪除,因此有可能會被非法存取。`LIST_POISONING` 是將被刪除的節點的 prev & next 先指向一個定義好的節點以避免這種狀況。
* linked list 採用環狀是基於哪些考量?
* 可從兩個面向來考量這樣的設計,[參考資料](https://www.quora.com/Why-are-all-the-linked-lists-circular-in-the-Linux-Kernel)
* singly or doubly
* doubly linked list 雖然會花費較多的儲存空間,但相較於他在實作上的便利性,空間的差別顯的微不足道。
* 例如:實作刪除特定節點的前一節點時,若使用 singly 可能需要多一個暫存指標來存 current node 的上一個節點;但使用 doubly 可以很直觀的 trace 到目標後再 ->prev 即可
* circular or non-circular
* 雖然多數的狀況其實是使用 non-circular,但其實 circular 也沒有多使用其他資源,只是將尾節點指向頭
* circular doubly-linked list 擁有四種不同情況的所有優點,且沒有顯著的空間差別,因此 linux 採用這種設計
* `list_for_each_safe` 和 `list_for_each` 的差異在哪?“safe” 在執行時期的影響為何?
* 參考 [list\_for\_each()與list\_for\_each_safe()的區別](https://blog.csdn.net/choice_jj/article/details/7496732)
* safe 版本會將目前存取的節點 (pos) 的下個節點備份到 n ,以避免在 list_del(pos) 時使 pos->prev 及 pos->next 成為 undefined state,在 list_del_init(pos) 時使得 pos 前後節點產生自身循環
* for_each 風格的開發方式對程式開發者的影響為何?
* 提示:對照其他程式語言,如 Perl 和 Python
>[color=green]TODO
* 程式註解裡頭大量存在 `@` 符號,這有何意義?你能否應用在後續的程式開發呢?
* 提示: 對照看 Doxygen
* Doxygen 是一個可以將程式碼中註解轉成文檔的工具,@ 為這種工具的指令開頭
* `tests/` 目錄底下的 unit test 的作用為何?就軟體工程來說的精神為何?
* 檢驗 list.h 中的 macro 是否運作正確,如果運作失敗或結果有誤會在 assert() 被擋下來
* 根據 [維基百科](https://en.wikipedia.org/wiki/Unit_testing) 對 unit test 的定義:
In computer programming, unit testing is a software testing method by which individual units of source code, sets of one or more computer program modules together with associated control data, usage procedures, and operating procedures, are **tested to determine whether they are fit for use**
* 所以我認為應該是為了確保這段程式碼是正確並可達到預期效用的,如果開發到一個階段沒有經過測試,後面就繼續使用可能造成大量錯誤的結果
* `tests/` 目錄的 unit test 可如何持續精進和改善呢?
* 或許可以考慮在 Makefile 中增加一個執行 `tests/` 中所有 unit test 的 target 或寫一個 script 來執行全部檔案。因為如果對某個功能做修改,而這個功能又會被其他功能使用的話,嚴謹一點的作法應該要每個 unit test 都執行看看以確保其他功能不會受影響,手動輸入會蠻花時間的。如果要這樣改善的話應該還要在 assert() 中加上 file 名以方便 debug
## 針對 linked list 的排序演算法
研讀 [A Comparative Study Of Linked List Sorting Algorithms](https://www.researchgate.net/publication/2434273_A_Comparative_Study_Of_Linked_List_Sorting_Algorithms)
- [ ] 自我檢查事項
* 對 linked list 進行排序的應用場合為何?
* 顯示 Cpu process
* 考慮到 linked list 在某些場合幾乎都是幾乎排序完成,這樣貿然套用 quick sort 會有什麼問題?如何確保在平均和最差的時間複雜度呢?
* 若原本資料分佈接近反向排序, quick sort 會將時間複雜度拉高到 $O(n^2)$
* 能否找出 Linux 核心原始程式碼裡頭,對 linked list 排序的案例?
* [linux/list_sort.h](https://github.com/torvalds/linux/blob/master/include/linux/list_sort.h)
* 透過 [skiplist](https://en.wikipedia.org/wiki/Skip_list) 這樣的變形,能否加速排序?
* 研讀 [How to find the kth largest element in an unsorted array of length n in O(n)?](https://stackoverflow.com/questions/251781/how-to-find-the-kth-largest-element-in-an-unsorted-array-of-length-n-in-on),比照上方連結,是否能設計出針對 linked list 有效找出第 k 大 (或小) 元素的演算法?
* [linux-list](https://github.com/sysprog21/linux-list) 裡頭 `examples` 裡頭有兩種排序實作 (insertion 和 quick sort),請簡述其原理
## 其他要求
* 在 GitHub 上 fork [linux-list](https://github.com/sysprog21/linux-list),參考 `examples/insert-sort.c` 和 `examples/quick-sort.c` 的實作方式,實作 merge sort,並且在 `tests/` 目錄提供新的 unit test
* 研讀「你所不知道的 C 語言」的 [函式呼叫篇](https://hackmd.io/s/SJ6hRj-zg) 和 [技巧篇](https://hackmd.io/s/HyIdoLnjl) 探討 [linux-list](https://github.com/sysprog21/linux-list) 的 `include/list.h` 的實作考量 (在上述檢查清單已提及部分)
* 承上,實作測試程式,批次建立包含若干大小的 linked list,隨機放入數值為介於 1 到 366 之間 (包含) 的節點 (代表 [day number](https://www.epochconverter.com/daynumbers)) ,至少應該涵蓋 10^1^, 10^2^, 10^3^, ... 10^6^ 等數量,透過前述的 insert, quick, merge sort 進行排序,分析執行時間並解讀其行為
* 因為要實作 merge sort 所以想先寫個可以存取 list 中第 nth node 的 macro ,但編譯不成功,只好放棄使用 macro
```=
#define NTH_IN_LIST(head,n) \
for(;n>0; head=head->next,n--);
```
error:
```shell
error: expected expression before ‘for’
for(;n>0; head=head->next,n--);
^
```
* 承上,設計 deduplication 程式,將上述輸入中的數值挑出重複的節點並與刪除,透過統計分析,解讀執行時間分佈,以及探討 [data deduplication](https://en.wikipedia.org/wiki/Data_deduplication) 的效益
* 比照生日悖論,提出統計模型和數學分析
* 參照 [Remove duplicates from a sorted linked list](https://www.geeksforgeeks.org/remove-duplicates-from-a-sorted-linked-list/)
* 延續 [A Comparative Study Of Linked List Sorting Algorithms](https://www.researchgate.net/publication/2434273_8_Comparative_Study_Of_Linked_List_Sorting_Algorithms) 的方式,量化分析上述步驟,並且提出效能改善機制
###### tags: `bauuuu1021`, `sysprog`, `2018spring`
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet