2017q3 Homework1 (ternary)

contributed by <yusihlin>

Reviewed by tina0405

• 在介紹真值表，和電路實現上很清楚，只可惜缺乏實際應用的案例和對針對程式碼需求的修改

Balanced Ternary 介紹

三位元數值系統由三種符號組成，直觀上會以 0,1,2 來表示三進制，然而 Balanced Ternary 以 -1,0,+1 三種符號代表，由於 -1 的存在不需多餘的符號即可表示負數。

數值轉換

（-1 記為 T）

$\begin{array}{rl}{193}_{dec}& =1\times 2^7+1\times 2^6+0\times 2^5+0\times 2^4+0\times 2^3+0\times 2^2+0\times 2^1+1\times 2^0={11000001}_2\\ & =2\times 3^4+1\times 3^3+0\times 3^2+1\times 3^1+1\times 3^0={21011}_3\\ & =1\times 3^5+(-1)\times 3^4+1\times 3^3+0\times 3^2+1\times 3^1+1\times 3^0=1T{1011}_{bal3}\end{array}$

• 透過觀察可知使用 2 進位表示 193 這個數字需要 8 個位元，而使用 Balanced Ternary 只需要 6 個位元，至於
  ${21011}_3$ 到
  $1T{1011}_{bal3}$ 的轉換可以參考 zhanyangch 同學的共筆，根據
  $2\times 3^k=(3-1)\times 3^k=1\times 3^{k+1}+(-1)\times 3^k$ 我們可以用1T表示2(同理可用T1表示 -2)，在 wikipedia 中對 Balanced Ternary 的介紹還有一種方法是先 +1 並允許進位，接著再 -1 不允許借位，本來範圍由 0,1,2 平移到 -1,0,1 ，以下為說明：
  
  $$\begin{gathered} {21011}_3+{11111}_3={102122}_3 \\ {102122}_3-{11111}_3=1T{1011}_{bal3} \end{gathered}$$

$-{193}_{dec}=(-1)\times 3^5+1\times 3^4+(-1)\times 3^3+0\times 3^2+(-1)\times 3^1+(-1)\times 3^0=T1T0T{T}_{bal3}$

• 由正負數的比較可以看出差別只在 +1 和 -1 的對換，優點是不用像二進位需透過補數來表示負數。

運算

• 邏輯概念：如果 Ternary 的3個邏輯概念為 true, unknown, false ，則會有以下關係

  Balanced	Logic	Unsigned
  T	False	0
  0	Unknown	1
  1	True	2

• 邏輯 NOT, AND, OR, XOR

  • NOT

    $a$	$\overline{a}$
    T	1
    0	0
    1	T

  • Min or AND

    c	T	0	1
    T	T	T	T
    0	T	0	0
    1	T	0	1
    $c=(a\wedge b)=min(a,b)$

  • Max or OR

    c	T	0	1
    T	T	0	1
    0	0	0	1
    1	1	1	1
    $c=(a\vee b)=max(a,b)$

  $$\begin{gathered} (a\vee b)=-(-a\wedge -b)ormax(a,b)=-min(-a,-b) \\ (a\wedge b)=-(-a\vee -b)ormin(a,b)=-max(-a,-b) \end{gathered}$$
  滿足 DeMorgan's laws ，所以我們只需 max 或 min 並將符號反相即可得另一個。

  • XOR

    c	T	0	1
    T	T	0	1
    0	0	0	0
    1	1	0	T
    $c=(a\oplus b)$

• 加法器

  • Half-adder

    ${\mathbf{a}}_{\mathbf{i}}$	${\mathbf{b}}_{\mathbf{i}}$	${\mathbf{s}}_{\mathbf{i}}$	${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$
    T	T	1	T
    T	0	T	0
    T	1	0	0
    0	T	T	0
    0	0	0	0
    0	1	1	0
    1	T	0	0
    1	0	1	0
    1	1	T	1
    分別看 ${\mathbf{s}}_{\mathbf{i}}$ 和 ${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$

    ${\mathbf{s}}_{\mathbf{i}}$	T	0	1
    T	1	T	0
    0	T	0	1
    1	0	1	T
    $s_i=(a+b)=((a=T)\wedge (b-1))\vee ((a=0)\wedge (b))\wedge ((a=1)\vee (b+1))$

    在二進位中我們是以

    ${\mathbf{s}}_{\mathbf{i}}\mathbf{=}{\mathbf{a}}_{\mathbf{i}}\oplus {\mathbf{b}}_{\mathbf{i}}$ 來表示，但由真值表可看出

    ${\mathbf{s}}_{\mathbf{i}}\ne {\mathbf{a}}_{\mathbf{i}}\oplus {\mathbf{b}}_{\mathbf{i}}$

    當我們以 Sum-of-products canonical form 做化簡時 T 會被消除，此時剩下 6 個 minterms ，在布林邏輯中每個 minterms 有兩個輸入，但在這裡我們增加一個輸入常數以指向最後的輸出，所以會變成
    

    $\begin{array}{rl}{s}_i=(a+b)& =((a=T)\wedge (b=T))\wedge 1)\\ & \vee ((a=T)\wedge (b=1))\wedge 0)\\ & \vee ((a=0)\wedge (b=0))\wedge 0)\\ & \vee ((a=0)\wedge (b=1))\wedge 1)\\ & \vee ((a=1)\wedge (b=T))\wedge 0)\\ & \vee ((a=1)\wedge (b=0))\wedge 1)\end{array}$

    ${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$	T	0	1
    T	T	0	0
    0	0	0	0
    1	0	0	1
    $c_{i+1}=a⊠b=(a\wedge b)\vee ((a\ne T)\wedge 0)\vee ((b\ne T)\wedge 0)$

    同理

    ${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$ 也不像二進位為 a & b ，用前面的方法化簡的話會有 8 個 minterms ，這裡就不再列出。
    雖說 Balanced Ternary 的空間使用度較佳，但也因為多狀態的存在使得電路設計複雜的多。

    有了真值表後我們需要構建一個基本構件以實現半加法器，參考 Ternary computing: basics 設計了一個多工器，輸入一個進行基本運算的變數輸出對應的功能 ( unary function ) ， 5 個引腳中一個接收三位元的輸入， inN, inO, inP 根據多工器所需功能而設定以產生相應的輸出。

    
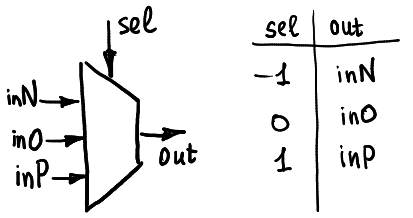
    透過上面的真值表設計 4 個不同功能的多工器 A+1, A+1, max(A,0), min(A,0) ，以下拿 max(A,0) 做說明
    
    前面已推導出 max 的真值表，這邊我們輸入 A 做引數，另一個輸入 B 為 0 ，則由真值表截取 B = 0 那行應有的輸出為 (0,0,1)，所以如果我們要做出有 max(A,1) 的多工器，則產生的輸出應為 (1,1,1) 當作 inN, inO, inP 的輸入。
    接下來就能透過多工器實現

    ${\mathbf{s}}_{\mathbf{i}}$ 和
    ${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$
    
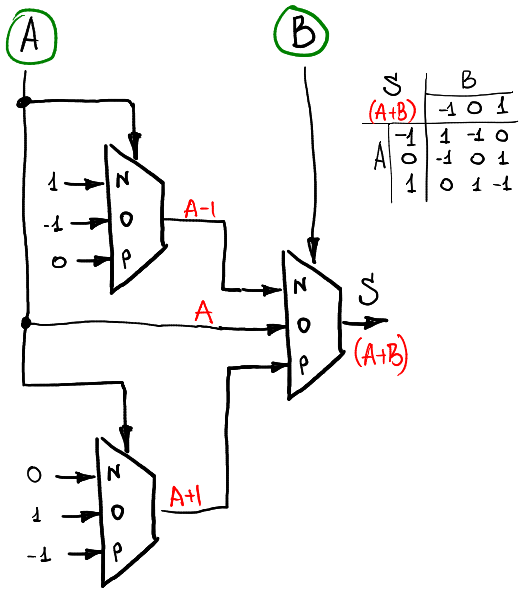
    這邊看會比較複雜一點，首先看真值表，不看 A 當 B 的輸入 (-1,0,1) 各會產生三個輸出，當 B 為 -1 時，需傳入的輸入為 (1,-1,0) ，所以在前一層我們須使用功能為 A-1 的多工器傳入第二層的 inN ，依此類推 inO 傳入 (-1,0,1) 也就是 A ， inP 傳入 (0,1,-1) 也就是 A+1。
    
    
    ${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$ 的部分由真值表也可以知道分別需傳入 ( min(A,0),0,max(A,0) ) 以產生對應的真值表。

  • Full-adder

    與半加法器相較全加法器有三個輸入

    $\mathbf{A}\mathbf{,}\mathbf{B}\mathbf{,}{\mathbf{C}}_{\mathbf{in}}$ 及兩個輸出
    $\mathbf{S}\mathbf{,}{\mathbf{C}}_{\mathbf{out}}$
    
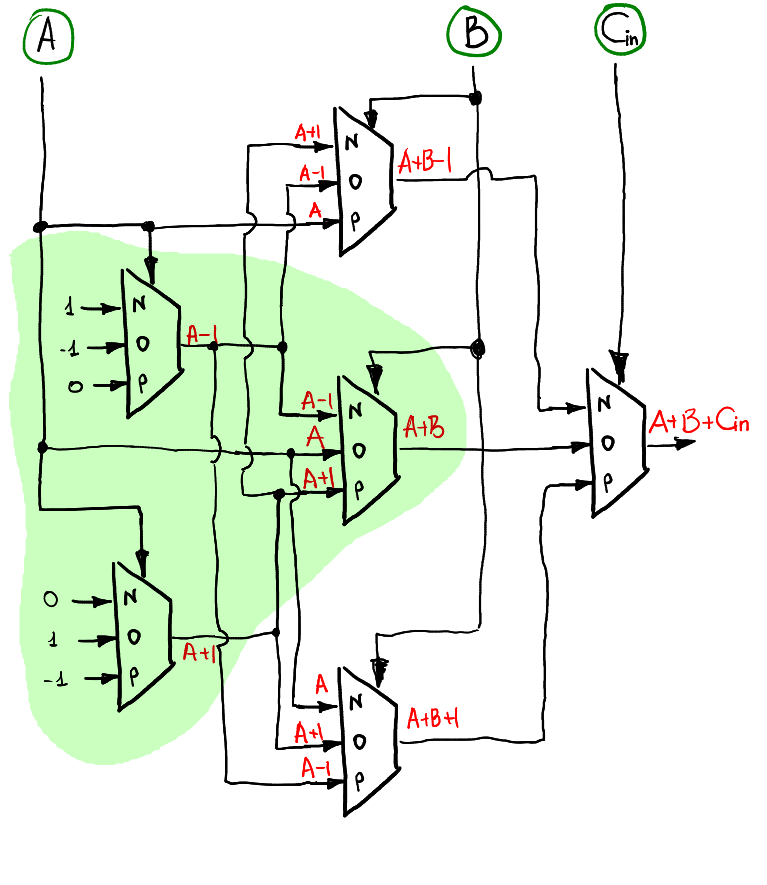
    S 的部分有三層，第一層輸入 A ，第二層輸入 B ，第三層輸入
    ${\mathbf{C}}_{\mathbf{in}}$ ，因此 function 為
    $\mathbf{(}\mathbf{A}\mathbf{+}\mathbf{B}\mathbf{+}{\mathbf{C}}_{\mathbf{in}}\mathbf{)}$ ，將各層展開為圖中紅色字體，綠色區域為原本的半加法器，當
    ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{0}$ 時會退化成半加法器。
    
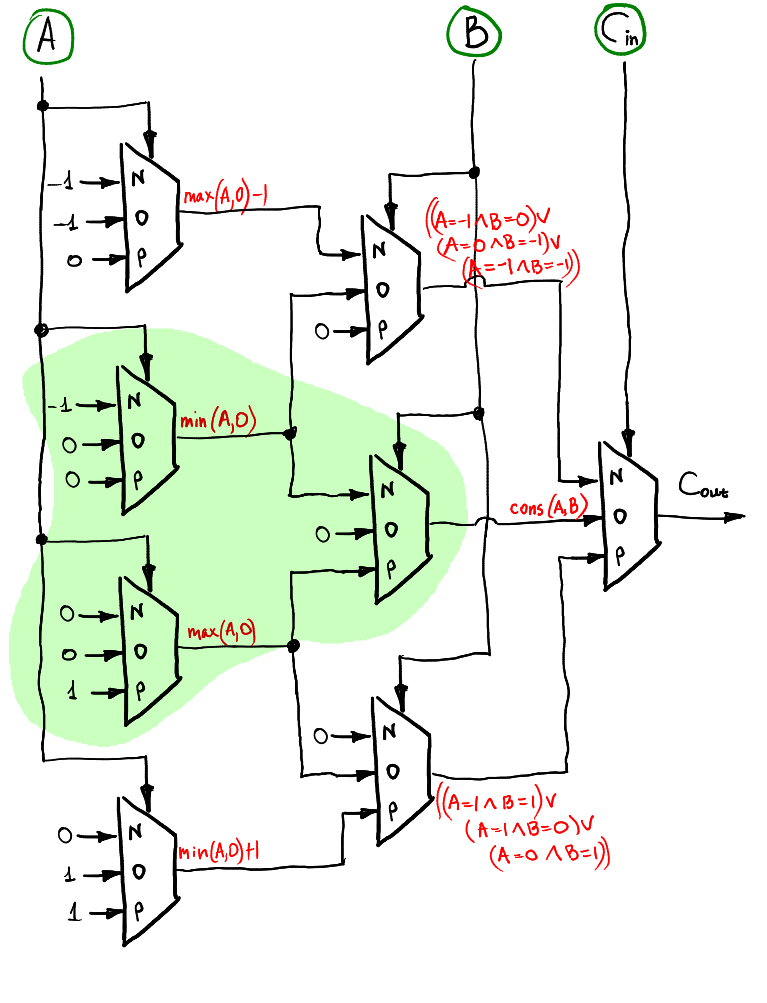
    前面 S 的部分可以直接看出，在看
    ${\mathbf{C}}_{\mathbf{out}}$ 要搭配 真值表，然後將
    ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{(}\mathbf{T}\mathbf{,}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{)}$ 的部分取出來看

    ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{T}$	T	0	1
    T	T	T	0
    0	T	0	0
    1	0	0	0
    當 ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{T}$ 時有三個組合對應 (A,B) 分別為 (T,T),(T,0),(0,T)
    ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{0}$	T	0	1
    :–––––––––-:	-	-	-
    T	T	0	0
    0	0	0	0
    1	0	0	1
    當 ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{0}$ 時與半加法器的 ${\mathbf{c}}_{\mathbf{i}\mathbf{+}\mathbf{1}}$ 相同
    ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{1}$	T	0	1
    :–––––––––-:	-	-	-
    T	0	0	0
    0	0	0	1
    1	0	1	1
    當 ${\mathbf{C}}_{\mathbf{in}}\mathbf{=}\mathbf{1}$ 時有三個組合對應 (A,B) 分別為 (0,1),(1,0),(1,1)

Balanced Ternary 的設計要解決甚麼類型的問題

Radix Economy

基需 (Radix Economy) 的概念是指在一個固定基數下表示一個數需要的開銷。在表示一個數時同時考慮到基數與位數，例如要表示 0~9 時在基數為 2 下需要 4 位數，在基數為 10 下只需要 1 位數，綜合考量下對基需有明確定義，對於任意數 N，在基數為 R 下表示數字需要

$lo{g}_{r}N+1$ 位數，也就是

$E(r,N)=r\times (lo{g}_{r}N+1)$
把上式看成連續函數的極值問題

$E(r,N)=r\times (lo{g}_{r}N+1)\approx r\times (lo{g}_{r}N)=(r/ln(r))\times ln(N)$
則可以發現當 r = e 時值最小，再來是 3, 2, 4

透過數學證明在整數上三進制是最經濟的進制，可是為何如今的計算機結構仍採用二進制？在 The most efficient radix is not e 中對於 Radix Economy 有其他的看法

要判斷哪個基數比另一個更有效取決於你想表達的數字，這意味著如果你想要表示

$N$ 個值的範圍，則可以最有效地表示這些值的基數

$R$ 是對於某些

$k$，

$R^k$ 最接近於

$N$ 的基數

$R$ ，他們可能是 2,3 或是 10，這一切都取決於

$N$ ，當

$N=10$ 為 radix-10 因為

$10={10}^1$，當

$N=64$，則有

$64=2^6=4^3=8^2$。

如果這樣不就意味著最好的基數總會是想表達的數字 N 本身嗎？事實上的確是如此，但當你要使用它時必須先構建出可以與其搭配的硬體，基數越大難以量化，這表示為了實際目的 R 不能太大。
來比較 radix-2 [2, 4, 8, 16, 32, 64…]和 radix-3 [3, 9, 27, 81, 243, 729…]，選擇一個隨機數 N，你可以預期 N 到下一個

$2^k$ 的距離較

$3^k$ 小，隨著基數增長差距越來越大。

參考文獻

• Douglas W. Jones on Ternary Logic
• 三生萬物
• Brian Hayes_Third Base(待閱讀)
• 【獨家】化學計算、濕件計算、流體計算和三元計算,這些「非常規計算」將挑戰摩爾定律(待整理)