# 2017q3 Homework1 (ternary)
###### tags: `sysprog2017` `dev_record`
contributed by <`HTYISABUG`>

---

## 解釋 Balanced Ternary 原理
- [x] 解釋 Balanced Ternary 原理

在課程中已經知道知道 Balanced Ternary 是由`-`, `0`, `+`，3個狀態來表達數字的數值系統。

> TODO: 詳細閱讀 [Fast Ternary Addition](http://homepage.divms.uiowa.edu/~jones/ternary/arith.shtml)，理解 base-3 的原理 (並且複習數位邏輯)，整理 base-3 基礎運算操作
> [name="jserv"][color=red]

考慮 `136` 在 Decimal，Binary，Ternary，Balanced Ternary 的情況

|Decimal|Binary |Ternary|Balanced Ternary|
|:-----:|:--------:|:-----:|:--------------:|
|$136$ |$10001000$|$12001$|$2-00+$ |

Binary:
$2^7+2^3$
Ternary:
$3^4+2\times 3^3+3^0$
Balanced Ternary:
$2\times 3^4-3^3+3^0$

這樣看下來，Ternary 能用較少位數表達更多位的 binary code
稍微計算一下
* unsigned binary
* 8 bits: $0-255$
* 16bits: $0-65535$
* unsigned ternary
* 5 bits: $0-243$
* 10bits: $0-59048$

可以得知 5bits ternary 就能大約表達 8bits binary
然後 10bits 大約能表達 16bits binary

再考慮一下浮點數的狀況
以 ternary 表達浮點數
若以 9bits 表達 exponent, 18bits 表達 mantissa
這 27bits 能提供超過 8 位的小數點後精確度
相比之下, binary 32bits 只能提供 5 位

由此可以得知, 採用 ternary 表達數字能縮小所需空間及提升精確度

----

:::info
### Radix economy
由 ternary 能看出採用比較大的底數能用比較少位數表達一個數
能用多少位表達一個數被稱為 **radix economy**
那麼是不是底數愈大, radix economy 就越好呢?

計算 radix economy 的公式如下
$E(b, N)=b\lfloor log_b(N)+1\rfloor$
$b$ 為底數, $N$ 為要表達的數字
將 $N$ 看做常數對 $b$ 微分, 結果為下圖


可以看到 $b$ 的斜率在 $e$ 為 `0`
所以以 $e$ 當作 base 的話 radix economy 最低

下表為其他 base 與 base-$e$ 比較的結果


base-2 和 base-3 僅次於 base-$e$，而底數越大就越差。
這應該也是採用 Ternary 當數值系統的原因之一。
:::

> TODO: 論述方式請參考 [Ternary Number Systems](http://homepage.divms.uiowa.edu/~jones/ternary/numbers.shtml) 的手法
> [name="jserv"][color=red]

> 繼續研讀 [What is the most efficient numerical base system?](https://math.stackexchange.com/questions/446664/what-is-the-most-efficient-numerical-base-system)，並依據裡頭的分析，量化上述討論
> [name="jserv"][color=red]

----

那麼 Balanced Ternary 又是怎麼回事？
Balanced Ternary 的位數表達有時比 Ternary 多
但其價值在考慮到負數的情況下才會體現出來。

考慮 `-108` 在 Decimal，Binary，Ternary，Balanced Ternary 的情況

|Decimal|Binary |Ternary |Balanced Ternary|
|:-----:|:--------:|:------:|:--------------:|
|$-108$ |$-1101100$|$-11000$|$--000$ |

Balanced Ternary 的優點就體現出來了。其他數值系統還至少要多用一位儲存正負，而 Balanced Ternary 是在編碼時就將正負包含進去，這樣一看反而使用位數更少。

基於這樣的特性，Balanced Ternary 在正負轉換時也更簡單，只要將所有的位數都正負互換就行了。這樣的特性不只在整數，浮點數也通用。

> 請搭配閱讀 [三生萬物](http://www.global-sci.org/mc/issues/5/no4/freepdf/79s.pdf)，裡頭有延伸 radix economy 的思考，也提及 SQL 處理 NaN 時，用到 base-3
> [name="jserv"][color=red]

----

### 運算
#### Add, Sub, Mul, Div
|+ |$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$\bar 11$|$\bar 1$ |$0$ |
|$0$ |$\bar 1$ |$0$ |$1$ |
|$1$ |$0$ |$1$ |$1\bar 1$ |

|- |$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$0$ |$\bar 1$ |$\bar 11$ |
|$0$ |$1$ |$0$ |$\bar 1$ |
|$1$ |$1\bar 1$|$1$ |$0$ |

|$\times$|$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$1$ |$0$ |$\bar 1$ |
|$0$ |$0$ |$0$ |$0$ |
|$1$ |$\bar 1$ |$0$ |$1$ |

|$\div$ |$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$1$ |$NaN$ |$\bar 1$ |
|$0$ |$0$ |$NaN$ |$0$ |
|$1$ |$\bar 1$ |$NaN$ |$1$ |

#### Ternary Truth Table
Ternary 有三種數值, 在真值表中以:`-` = false, `0` = unknown, `+` = true 標記

|NOT| |
|---|-|
|F |T|
|U |U|
|T |F|

|AND|F|U|T|
|---|-|-|-|
|F |F|F|F|
|U |F|U|U|
|T |F|U|T|

|OR |F|U|T|
|---|-|-|-|
|F |F|U|T|
|U |U|U|T|
|T |T|T|T|

3 張真值表分別可以對應到 NEG, MIN, MAX 操作

----

### Ternary 電路實作
[Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics) 的作者設計了以 balanced ternary 運作的計算電路
以 3 個輸入的 multiplexer 為基礎
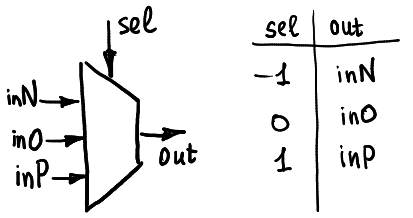
藉由改變輸入訊號能得到不同的結果

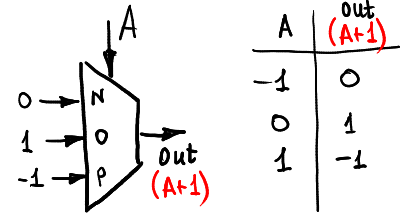
#### Unary Function
作者先定義了幾個單一輸入元的 function
* increment
* 
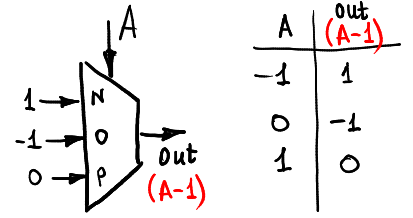
* decrement
* 
* max(x, 0)
* .png)
* min(x, 0)
* .png)

#### Half Adder
再來要以 ternary multiplexer 與以上 function 實作出 half adder
half adder 真值表如下
|A \ B |$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$1$ |$\bar 1$ |$0$ |
|$0$ |$\bar 1$ |$0$ |$1$ |
|$1$ |$0$ |$1$ |$\bar 1$ |

先代入把情況列出來看看: `A+-1`, `A+0`, `A+1`
可以化簡成 `A-1`, `A`, `A+1`
所以至少有個以 B 為選擇訊號的 mux (mux B) 對應這三種狀況
再把這三種狀況以定義好的 function 代入就能得到下圖

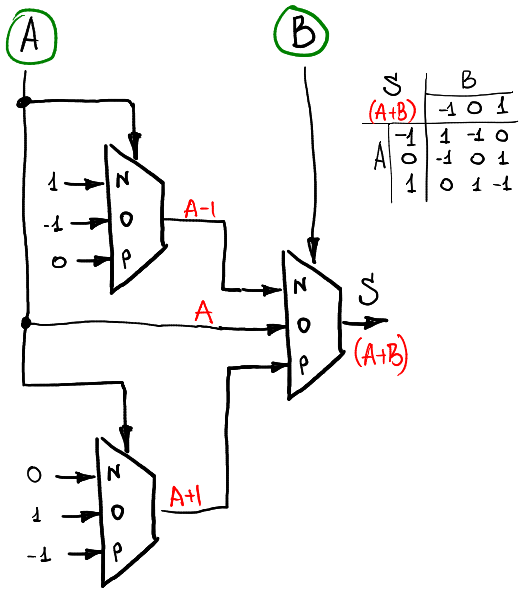
#### Consensus
若要兜成 full adder, 除了 half adder 還需要計算 carry
carry 真值表如下
|A \ B |$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$\bar 1$ |$0$ |$0$ |
|$0$ |$0$ |$0$ |$0$ |
|$1$ |$0$ |$0$ |$1$ |

用思考 half adder 的方式來看
對應 mux B 的三種情況為 `min(A, 0)`, `0`, `max(A, 0)`
同樣以 function 代入得下圖
.png)

#### Full Adder
Binary 的 full adder 是由兩個 half adder 組合成的
Ternary full adder 不太一樣
Full adder 分層運作:
1. 以 `A` 為 selector 計算
2. 以 `B` 為 selector 計算
3. 以 `C` 為 selector 計算
每一層的 input 都會取自前一層的結果, 第一層是常數
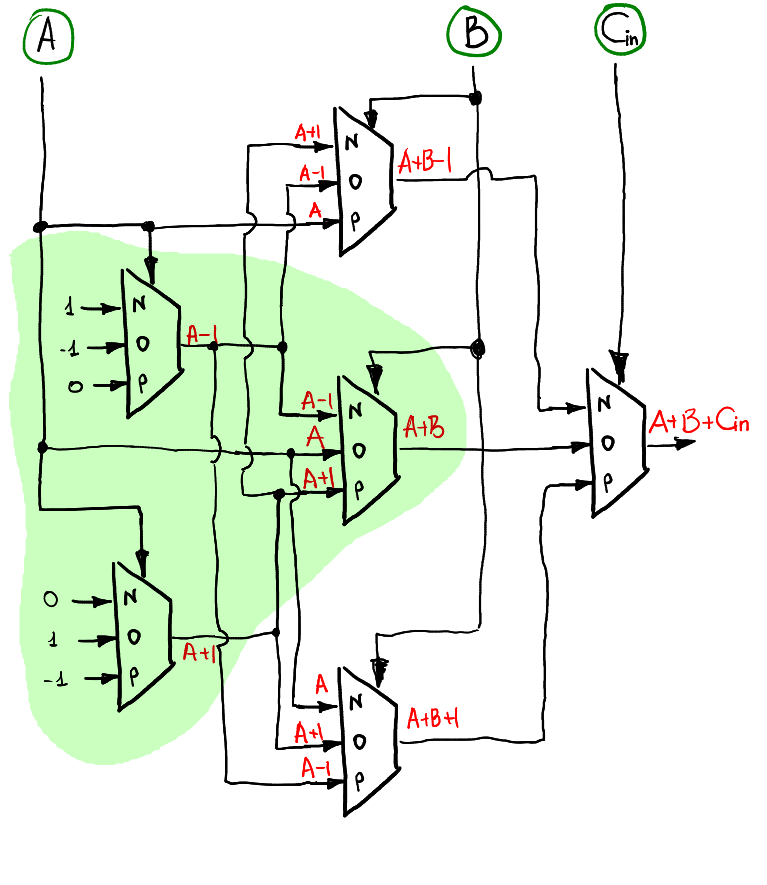
綠色部份是一個 half adder
不只這一部份, 其實每層之間都是幾個 half adder 交錯排列

:::info
至於為什麼不像 binary adder 那樣用 xor, and 來實作
列出真值表就知道了......
And 前面已列出
|xor |$\bar 1$ |$0$ |$1$ |
|--------|---------|---------|----------|
|$\bar 1$|$\bar 1$ |$0$ |$1$ |
|$0$ |$0$ |$0$ |$0$ |
|$1$ |$1$ |$0$ |$\bar 1$ |

xor 跟 add, and 跟 carry 所需的數值完全不同
所以 $sum = x \oplus y, carry = x \& y$ 這套在 ternary 行不通
:::

#### Overflow
跟 full adder 一樣是分層運作
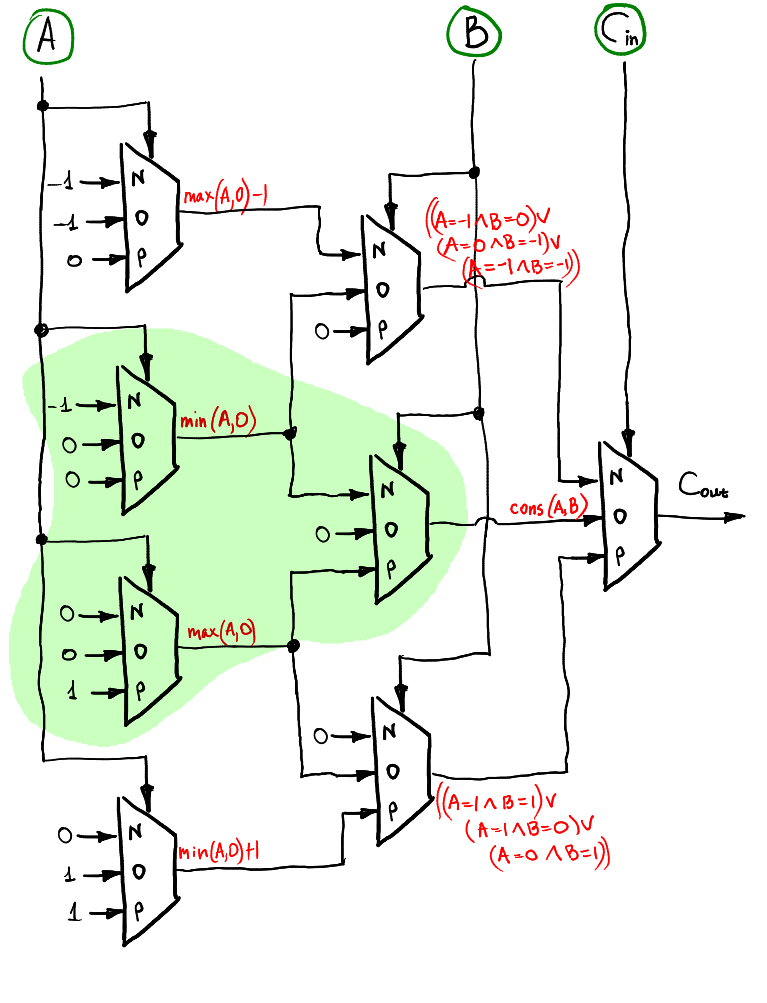
綠色部份同樣是一個取進位的電路, 每層也都是交錯排列

> 請閱讀 [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)，關注於 ternary multiplexer, Unary functions, half-adder, Consensus, full adder, Overflow
> [name="jserv][color=blue]

---

## Balanced Ternary 的設計要解決什麼類型的問題
- [ ] Balanced Ternary 的設計要解決什麼類型的問題，需要詳述實際應用案例 (如 IOTA/Tangle)。提示：從算術表達的精準度和空間使用效率去探討

---

## 在 GitHub 裡頭可找到的應用案例
- [ ] 針對特定的領域 (如加密貨幣)，列出在 GitHub 裡頭可找到的應用案例，不僅列出程式碼，還要解說

---

## 參考資料
* [Balanced ternary (wikipedia)](https://en.wikipedia.org/wiki/Balanced_ternary)
* [Radix economy (wikipedia)](https://en.wikipedia.org/wiki/Radix_economy)
* [Ternary Number Systems](http://homepage.divms.uiowa.edu/~jones/ternary/numbers.shtml)
* [Ternary computing: basics](https://github.com/ssloy/tutorials/wiki/Ternary-computing:-basics)