# Leetcode刷題學習筆記 -- Binary Search Tree(BST)
## 簡介
ref : [wiki](https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%85%83%E6%90%9C%E5%B0%8B%E6%A8%B9)
二元搜尋樹（英語：Binary Search Tree），也稱為有序二元樹（ordered binary tree）或排序二元樹（sorted binary tree），是指一棵空樹或者具有下列性質的二元樹：

1. 若任意節點的左子樹不空，則左子樹上所有節點的值均小於它的根節點的值；
2. 若任意節點的右子樹不空，則右子樹上所有節點的值均大於它的根節點的值；
3. 任意節點的左、右子樹也分別為二元搜尋樹；


如果BST，呈現不平衡的狀態，例如都串在同一個直線。那最差情況都是O(n)。

| 演算法 | 平均 | 最差 |
| -------- | -------- | -------- |
| 空間 | O(n) | O(n) |
| 搜尋 | O(logn) | O(n) |
| 插入 | O(logn) | O(n) |
| 刪除 | O(logn) | O(n) |

二元搜尋樹的最壞效率是O(n)，但它支援動態查詢，且有很多改進版的二元搜尋樹可以使樹高為O(log n)，從而將最壞效率降至O(log n)，如==AVL樹==、==紅黑樹==等。

## Inorder Traversal
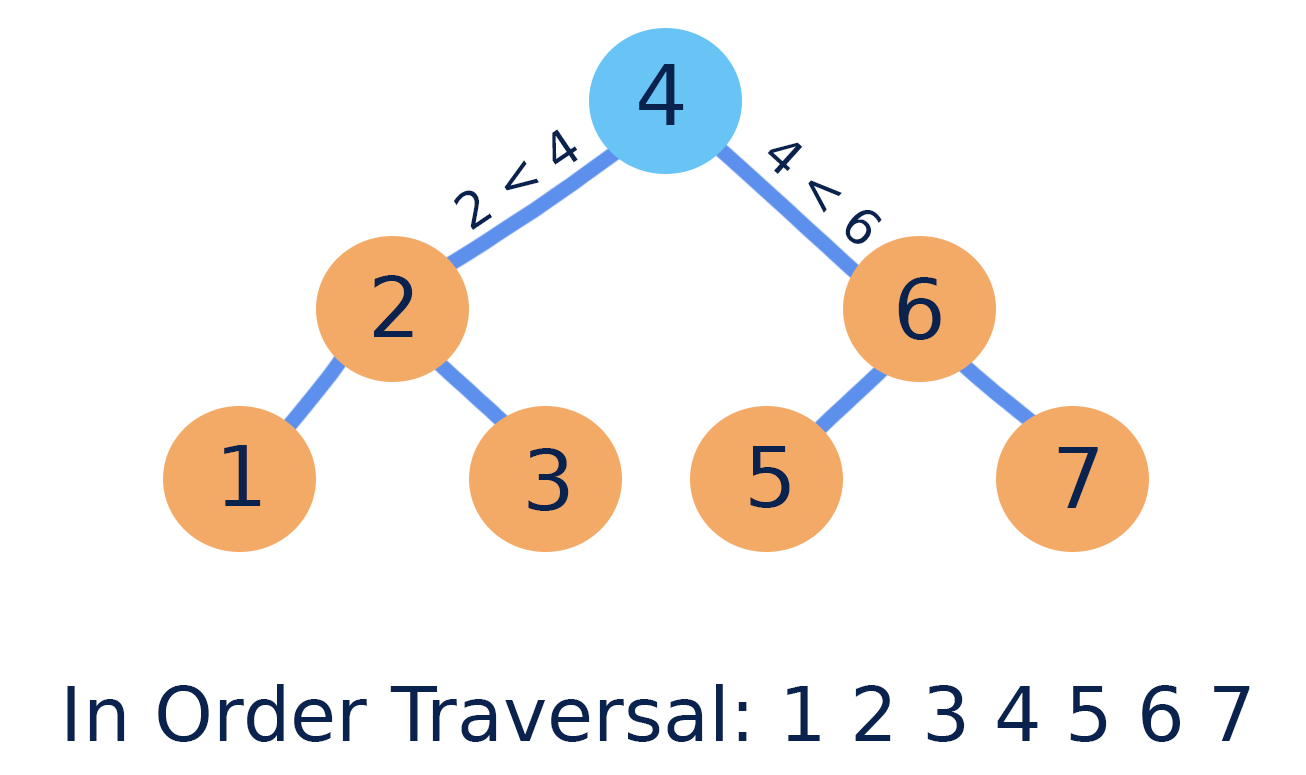
當BST(Binary Search Tree)使用Inorder Traversal的時候，可以得到遞增或是遞減的數列。

以下的程式碼是得到遞增序列。

void dfs(TreeNode *root, vector<int>& rtn) {
    if(!root) return;
    dfs(root->left);
    rtn.push_back(root->val);
    dfs(root->right);
}

以下的程式碼可以得到遞減序列。

void dfs(TreeNode *root, vector<int>& rtn) {
    if(!root) return;
    dfs(root->right);
    rtn.push_back(root->val);
    dfs(root->left);
}

另外也可以用stack來實現

void inorder(TreeNode *root) {
    stack<TreeNode *> st;
    TreeNode *p = root;
    while(p || !st.empty()) {
        // 先把全部的left存起來
        while(p) {
            st.push(p);
            p = p->left;
        }
        // 取出最後一個left node
        p = st.top(); st.pop();
        cout << p->val << endl;
        // 檢查right child node
        p = p->right;
    }
}

很多題目會根據上訴兩種來變形。
1. 遞增訪問
+ [230. Kth Smallest Element in a BST](/neNmzsZsRrmYQ-RtPWbYxA?both#230-Kth-Smallest-Element-in-a-BST)
+ [897. Increasing Order Search Tree](/neNmzsZsRrmYQ-RtPWbYxA?both#897-Increasing-Order-Search-Tree)
+ [99. Recover Binary Search Tree]()
2. 遞減訪問
+ [538. Convert BST to Greater Tree](/neNmzsZsRrmYQ-RtPWbYxA?both#538-Convert-BST-to-Greater-Tree)
3. 找兩個node之間最小的差
+ [783. Minimum Distance Between BST Nodes](/neNmzsZsRrmYQ-RtPWbYxA?both#783-Minimum-Distance-Between-BST-Nodes)
### [99. Recover Binary Search Tree](https://leetcode.com/problems/recover-binary-search-tree/)
在BST中有兩個node被交換了，試復原成原本的BST。

> 1. 使用inorder traversal。如果是正常的BST會得到從小到大的排列。
> 2. 題目只有兩個node被交換了，例如
> 1, 2, 3, 4, 5, 6 --> 1, **5**, 3, 4, **2**, 6
> 5, 3 --> prev > curr, 取前者
> 4, 2 --> prev > cur, 取後者

void recoverTree(TreeNode* root) {
    TreeNode *prev = nullptr, *first = nullptr, *second = nullptr, *p = root;
    stack<TreeNode *> st;
    while(p || !st.empty()) {
        while(p) {
            st.push(p);
            p = p->left;
        }
        p = st.top(); st.pop();
        if(prev && prev->val > p->val) {
            if(!first) first = prev; // 取前者
            second = p; // 取後者
        }
        prev = p;
        p = p->right;
    }
    swap(first->val, second->val);
}

### [230. Kth Smallest Element in a BST](https://leetcode.com/problems/kth-smallest-element-in-a-bst/)
找出BST中，第k個最小的值。

> 1. 在BST中使用Inorder Traversal來找出第k個數值。

class Solution {
    int k, rtn;
    void helper(TreeNode *root) {
        if(!root) return;
        helper(root->left);
        k--;
        if(k == 0) rtn = root->val;
        else if(k < 0) return;
        helper(root->right);
    }
public:
    int kthSmallest(TreeNode* root, int k) {
        this->k = k;
        helper(root);
        return rtn;
    }
};

### [897. Increasing Order Search Tree](https://leetcode.com/problems/increasing-order-search-tree/)
把BST，從小到大，依序串在node的右邊。

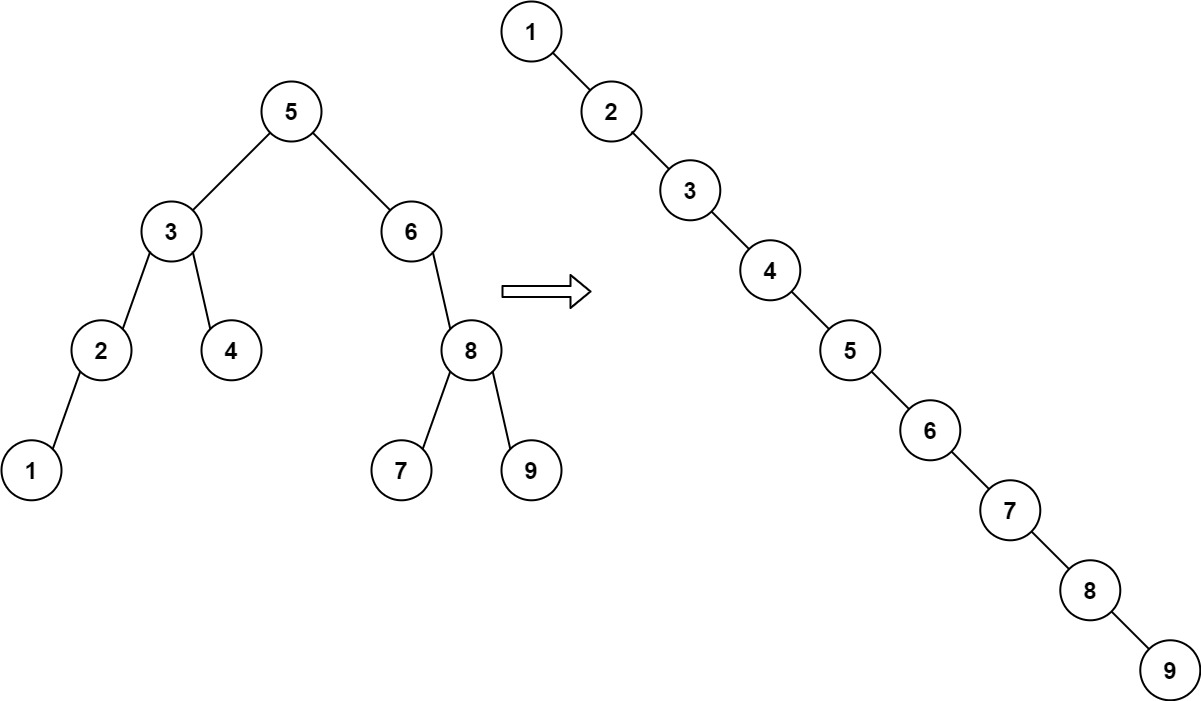
> 1. 對BST做Inorder Traversal。
> 2. 對每個node，把left child設成nullptr, 把right child設成下一個走訪的node。

class Solution {
    void helper(TreeNode *root) {
        if(!root) return;
        helper(root->left);
        root->left = nullptr;
        cur->right = root;
        cur = cur->right;
        helper(root->right);
    }
    TreeNode *cur;
public:
    TreeNode* increasingBST(TreeNode* root) {
        TreeNode *newroot = new TreeNode();
        cur = newroot;
        helper(root);
        return newroot->right;
    }
};

### [538. Convert BST to Greater Tree](https://leetcode.com/problems/convert-bst-to-greater-tree/)
給你一個BST，試給出一個Greater Tree。

> 1. 對BST做Inorder Traversal(從大到小)。
> 2. 每遇到一個node就把數值相加，並更新到目前的node。

class Solution {
    int sum = 0;
    void helper(TreeNode *root) {
        if(!root) return;
        helper(root->right);
        sum += root->val;
        root->val = sum;
        helper(root->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        helper(root);
        return root;
    }
};

### [450. Delete Node in a BST(Medium)](https://leetcode.com/problems/delete-node-in-a-bst/)
給你一個key，刪除BST中和key值一樣的node，並且保持原本的樹還是BST。

例如:
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]


解題思路:
> case 1: 如果要刪除的node是leaf，那就直接刪除。
> case 2: 如果要刪除的node不是leaf，但是只有一個child，則直接把child接上來。
> case 3: ==如果要刪除的node不是leaf，而且有兩個child!==，為了保持刪除後依然是BST，所以勢必要調整樹的結構。如何做到最小調整? ==使用右子樹最小值，或是左子樹最大值代替原本欲刪除的node，就可以達到最小的修正。==


TreeNode* deleteNode(TreeNode* root, int key) {
    if(!root) return nullptr;
    if(key > root->val)
        root->right = deleteNode(root->right, key);
    else if(key < root->val)
        root->left = deleteNode(root->left, key);
    else {
        // 只有一個child node，或是node為leaf
        if(!root->left || !root->right)
            root = root->left ? root->left : root->right;
        else {
            // node有兩個child
            // 找出右子樹最小值
            TreeNode *cur = root->right;
            while(cur->left) cur = cur->left;
            root->val = cur->val;
            // 刪除右子樹最小值的node
            root->right = deleteNode(root->right, cur->val);
        }
    }
    return root;
}

找出左邊子樹的最大值一樣也可以。

// 找出左子樹最大值
TreeNode *cur = root->left;
while(cur->right) cur = cur->right;
root->val = cur->val;
// 刪除左子樹最大值的node
root->left = deleteNode(root->left, cur->val);

### [235. Lowest Common Ancestor of a Binary Search Tree(Easy)](https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/)
給你兩個在BST中的node, p和q。找出這兩個的共同祖先(ancestor)。
> 1. 因為沒說明p, q是否有什麼關係，所以必須用max(), min()找出最大最小值。
> 2. root->val > max(p->val, q->val) 表示p和q都在root的左側。
> 3. root->val < min(p->val, q->val) 表示p和q都在root的右側。
> 4. 不是上述兩種狀況表示root即為共同的祖先。

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    if(!root) return nullptr;
    else if(root->val > max(p->val, q->val))
        return lowestCommonAncestor(root->left, p, q);
    else if(root->val < min(p->val, q->val))
        return lowestCommonAncestor(root->right, p, q);
    else // root->val > min(p->val, q->val) && root->val < max(p->val, q->val)
        return root;       
}

### [783. Minimum Distance Between BST Nodes](https://leetcode.com/problems/minimum-distance-between-bst-nodes/description/)
在BST中，找出兩個node之間最小的差。

> 1. 因為BST使用inorder traversal可以得到遞增數列，使用此特性比較前後兩個node，就可以找出最小的差值。

class Solution {
    // 在BST中使用inorder可以得到從小到大的排序。
    int ans = 1e5 + 1, prev = -1;
    void helper(TreeNode *root) {
        if(!root) return;
        helper(root->left);
        if(prev != -1)
            ans = min(ans, root->val - prev);
            
        prev = root->val;
        helper(root->right);
    }
public:
    int minDiffInBST(TreeNode* root) {
        helper(root);
        return ans;
    }
};

###### tags: `leetcode` `刷題`