# Honey I SNARKED the GPT

> Or rather how we got [nanoGPT](https://github.com/karpathy/nanoGPT) into Halo2-KZG circuits using [EZKL](https://github.com/zkonduit/ezkl).

> This post is written in collaboration with [Bianca Gănescu](https://twitter.com/BiancaGanescu) a Master's student at Imperial College London (supervised by [Jonathan Passerat-Palmbach](https://jopasser.at/)) who was instrumental in making this happen, and [Jason Morton](https://twitter.com/jasonmorton).

I am the lead developer on EZKL (stylized and pronounced *Ezekiel*), a library which enables users to convert computational graphs represented in the Open Neural Network Exchange (ONNX) format to a (**Halo2-KZG**) ZK-SNARK circuit. Since starting the project in August of 2022 we've come a long way in terms of the [breadth of models](https://github.com/zkonduit/ezkl/tree/main/examples) we support, our proving [performance](https://github.com/zkonduit/ezkl/actions/runs/5062656323/jobs/9088409174), and also the [community](https://t.me/+CoTsgokvJBQ2NWQx) of folks building and researching on top of our tool!

Bianca, as part of her Master's thesis, wanted to get nanoGPT into a ZK-SNARK using our tooling. This post is a high level overview of the steps it took to make that happen.

The sections below are somewhat technical and assume some knowledge of how the [Halo2 API](https://zcash.github.io/halo2/index.html) is structured.

### Supporting arbitrary model sizes


A question we often get is how we manage to get large models into a **Halo2-KZG** circuit for (almost) any arbitrary trusted setup size.

The way we've been able to deal with this is by having operations "wrap" around advice columns. To illustrate this consider our dot product argument:

| a0  | a1  | m     | s_dot | 
|-----|-----|-------|-------|
| x_i | y_i |m_{i-1}| s_dot |
|     |     |m_i    |       |

where constraints are such that $x_i*y_i + m_{i-1} = m_i$, and $i$ indexes over the elements of a vector or some other iterable structure.

Let's say $i$ exceeds the number of rows available in a single column (let's call that $M$). We start allocating the $x_i, y_i$ where $i > M$ to a new set of advice columns $a_2, a_3$. It requires some trickery in that we also need to map the result of the bottom of $a_0, a_1$ to the top of $a_2, a_3$ (by way of copy constraints), such that the constraint with a negative rotation of $-1$ still holds.

In this manner we can have a relatively large number of constraints by increasing the number of columns, rather than increasing the number of rows. The way we get around the region shuffling that may break this is (drum roll) .... we have a single region for the entire circuit and make sure to keep track of the current offset throughout.

Folks are often suprised that our code looks quite different to other Halo2 examples, and this single region strategy is why. As a side effect, it also has the nice property of leaking very little information about the architecture of the model, providing a kind of functional commitment.

### Supporting (almost) all Onnx operations

The ONNX format has over [100 operations](https://github.com/onnx/onnx/blob/main/docs/Operators.md) that it can represent. Our first approach was to painstakingly implement circuit constraint equivalents for each one at a time, dealing with high-dimensional tensor shape casting, and creating custom constraints and gates for each one.

That is until we discovered [tract](https://github.com/sonos/tract). Tract is a library developed by the Sonos team (and mainly the work of one savant [@kali](https://github.com/sonos/tract/commits?author=kali)), which reduces and prunes complex ONNX graphs into compositions of a small set of operations (the number of which is reducing with each new tract release). Instead of implementing 100+ operations we only need to implement 20 or so as equivalent circuit constraints.

In particular many linear operations such as matrix multiplication, column sum, outer product, dot product, transposition, transposed matrix multiplication, matrix to vector multiplication, Hadamard products, batched matrix multiplication, tensor contraction, even bilinear transformations over multiple tensors are represented as a single operation: the Einstein summation operation.

For those unfamiliar the Einstein summation convention is a powerful notation for expressing operations over multi-dimensional tensors. For a primer on it, I recommend this [article](https://towardsdatascience.com/einstein-index-notation-d62d48795378); but a brief summary is that by way of a succinct notational convention we can express any abitrary summation or product of elements between multidimensional tensors.

For instance to express matrix multiplication we might write:

ik,kj->ij,

which in effect expresses:
>we have 2 2D objects one with dimensionality `ik`, the other with dimensionality `kj` and our operation should produce an output of dimensionality `ij` by reducing along the common axis of dimensionality `k`.

For fun, here's another relationship this sort of notation can express:

bn,anm,bm->ba.

We leave this as an exercise for the reader to untangle what this represents :kissing_heart:.

Luckily the constraint equivalent of einsum is just a repeated application of the (generalized) argument of the dot product detailed above over the appropriate input axes. In follow up posts we'll release the exact construction of these constraints and arguments.

As such when we started to use tract in the backend, and implemented einsum, we were able to support a whole world of models out of the box including LSTMs and self-attention layers in transformer blocks (one of the constitutive elements of nanoGPT).

### Allowing for parallel region layouts in Halo2

Our "single region" strategy for Halo2, detailed above, means we are particularly well positioned to layout circuits in parallel. When dealing with 10million+ constraints, even generating circuit constraints or the witness can take some time and for the sake of user sanity / lack of patience we wanted to speed this process up.

Sadly the original implementation of Halo2 does not allow for parallel region layouts, and in particular the creation of the copy-constraints in the circuit are not deterministic in a multi-threaded setting. These copy constraints are expressed using "cycles", effectively directed graphs which have as constitutive elements all the Halo2 cells that should have equal witness values (i.e are copy-constrained).

Quoting the [Halo2 book](https://zcash.github.io/halo2/design/proving-system/permutation.html) directly:

> For example, suppose that we have a circuit that defines the following equality constraints: $a≡b, a≡c, d≡e$. From this we have the equality-constraint sets ${a,b,c}$ and ${d,e}$. We want to construct the permutation: $(a b c) (d e)$. This is expressed as two disjoint cycles $(a b c)$ and $(d e)$.

When two cells are copy-constrained, the cycles they are currently a part of are merged. For example, given two disjoint cycles $(A B C D)$ and $(E F G H)$ (diagrams taken from the Halo2 book):

A +---> B
^       +
|       |
+       v
D <---+ C       E +---> F
                ^       +
                |       |
                +       v
                H <---+ G

After adding constraint $B≡E$:

A +---> B +-------------+
^                       |
|                       |
+                       v
D <---+ C <---+ E       F
                ^       +
                |       |
                +       v
                H <---+ G

In particular, referring to step 2 of the algorithm in the [Halo2 Book](https://zcash.github.io/halo2/design/proving-system/permutation.html) for permutation arguments used to build copy-constraints:

> 2. Otherwise, left and right belong to different cycles. Make left the larger cycle and right the smaller one, by swapping them iff sizes(aux(left))<sizes(aux(right)).

The smaller "cycle" in a multi-threaded setting can be non-deterministic and as such, the constructed copy constraint labels can differ between the key generation and proof stage. For an illustration of how the order in which the copy constraints are generated can create different cycle directions see the below diagram (creds to me the artist):


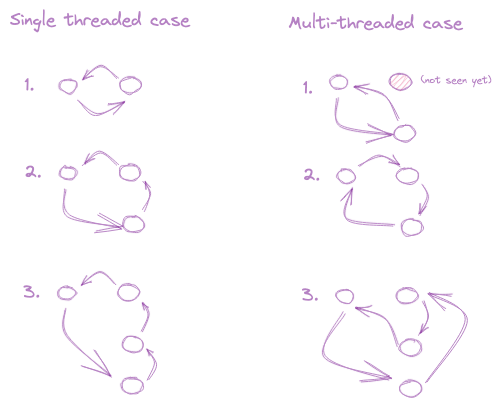
A way to mitigate this is to make this label deterministic which we do by way of the usage of different data structures for representing copy-constraint cycles in [this PR to PSE Halo2](https://github.com/privacy-scaling-explorations/halo2/pull/180).

Once we had this implemented we could generate the witness and layout circuit constraints in a parallel fashion.

### Rescaling fixed-point arithmetic

As Halo2 (and most ZK frameworks) operate over [Fields](https://en.wikipedia.org/wiki/Field_(mathematics)) we are somewhat constrained in the types of arithmetic we can easily (or cheaply) represent. For speed and convenience and codebase simplicity we currently perform operations using [fixed-point](https://en.wikipedia.org/wiki/Fixed-point_arithmetic) arithmetic.

Given a base $b$, a scale $s$ and a shift $k$, we represent a given decimal number $x$ as $b^{s}x + k$, which we then map to a member of the given field $\mathbb{F}$ we are operating over. As a default we choose $b=2, k=0$ and leave $s$ as a tunable parameter that can be set by the user.

The issue is that when composing lots of chained multiplicative operations, such as in deep networks like multi-head self-attention layers, the underlying scale of the fixed-point representation can _explode_. The result of the product has for scale the _sum_ of the input scales.

This poses a particular problem when used in conjunction with lookup tables. In particular we leverage fixed-column lookups to represent non-linear functions such as $ReLU$ or $e^x$. Ignoring cryptographic details, a lookup table is basically two advice columns, and two fixed columns of the Halo2 "grid." The fixed columns are pre-filled and committed at circuit definition time with all the allowed input-output pairs. The advice columns are filled at proving time, and an argument is made that all the input-output pairs in the witness are valid input-output pairs that appear in the pre-filled fixed columns.

Using random linear combination ideas, the argument conceptually reduces to looking up one advice column in one fixed column (image taken from [here](https://www.google.com/search?q=lookup+arguments+plonk&client=firefox-b-d&tbm=isch&sxsrf=APwXEdeFhRLzIsT2aIimkJjQwybX65wQtg:1684923063628&source=lnms&sa=X&ved=2ahUKEwjpsrnF243_AhWMQUEAHdngBNMQ_AUoAnoECAoQBA&biw=1512&bih=791&dpr=2#imgrc=K0HRIqcDMXVtFM)):


In the diagram above that corresponds to, say, the blue column and the orange one. When we say "$ReLU(x)$", what this means in a circuit is that the provided input-output witness values of $(x,ReLU(x))$ should be a row of the pre-committed lookup table.

When the fixed-point scale explodes in value, witness pairs can quickly fall out of range of our lookups. To keep this scale in control we introduce a heuristic scaling method where we periodically "divide-down" elements that have too large a fixed-point scale. This division is also performed using a lookup.

### nanoGPT in a SNARK

This combination of improvements mean we were able to get nanoGPT, exported as an Onnx file, [into a Halo2 circuit](https://github.com/zkonduit/ezkl/pull/255). Our latest benchmarks with public outputs and private model parameters and input data can be tracked [here](https://github.com/zkonduit/ezkl/actions/runs/5062656323/jobs/9088409174). In this setting we are proving a statement akin to:

> I ran this private nanoGPT-like model on some private data and it produced an output which matches this publicly known value.

We ran the benchmarks on the following spec:

CPU
    AMD Epyc 7413 - 24c/48t - 2.65 GHz/3.6 GHz 

RAM

    512 GB ECC 3200 MHz

    Data disks

    2×960 GB SSD NVMe

    Soft RAID

**Results:**

All tests were done with $K$ for the SRS generation such that "columns overflow", as detailed in the first section.

##### Tiny model (4 transformer layers ~ 250k parameters ~ 16 million constraints ~ $K=24$):

| | Description |
| ----------- | ----------- |
| verifying key generation | 382s |
| proving key generation | 850s |
| proof time | 1828s |
| verify time | 0s |

##### Small model (20 transformer layers ~ 1mil parameters ~ 64 million constraints ~ $K=24$):

| | Description |
| ----------- | ----------- |
| verifying key generation | 937s |
| proving key generation | 2106s |
| proof time | 5169s |
| verify time | 0s |

### Future work

We're excited to keep improving on these proving times. In particular we're excited to see where hardware acceleration can take us in terms of performance (creds to [@weikengchen](https://twitter.com/weikengchen) for a great discussion on this).

### Shoutouts to other similar work:

- Daniel Kang's [work](https://medium.com/@danieldkang/verified-execution-of-gpt-bert-clip-and-more-6acb693fd55f) of getting transformer models into Halo2.
- [Orion](https://github.com/gizatechxyz/orion), is a new ONNX runtime built with Cairo. The purpose is to provide a runtime implementation for verifiable ML model inferences using STARKs.
- [keras2circom](https://github.com/socathie/keras2circom) a library for converting keras models into circom circuits.
- [awesome-zkml](https://github.com/worldcoin/awesome-zkml) a repository of ZKML projects and resources.