---
tags: vaje, kirv, hash
hackmd: https://hackmd.io/klHFG502Rt29j094sjMKqw
plugins: mathjax
---
# Cryptography and computer security - Tutorial 5.1.2021

---

## Cryptographic hash functions

### Security notions

Hash function $H : {\lbrace 0, 1 \rbrace^*} \to \lbrace 0, 1 \rbrace^n$ deterministic

* **Preimage resistance**: given $y$, it is computationally infeasible to find an $x$ such that $H(x) = y$.
* **Second preimage resistance**: given $x$, it is computationally infeasible to find an $x' \ne x$ such that $H(x) = H(x')$.
* **Collision resistance**: it is computationally infeasible to find $x, x'$ such that $x \ne x'$ and $H(x) = H(x')$.

### Merkle-Damgård construction


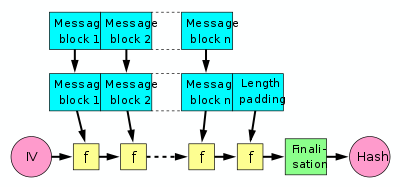
Examples:
* MD5 ($n = 128$)
* SHA-1 ($n = 160$)
* SHA-256, SHA-512
* SHA-3 (Keccak)
* BLAKE-3

---

### Exercise 1

Show that collision resistance implies second-preimage resistance of hash functions.

----

* Assume that $H$ is collision resistant.
* Assume that $H$ is not second preimage resistant.
- Given $x$, we can efficiently compute $x' \ne x$ such that $H(x) = H(x')$.
- Choose $x$, then we can find $x'$ as above.
- We have found a collision $(x, x')$ efficiently, contradiction.
* It follows that $H$ is second preimage resistant.

---

### Exercise 2

Let $g : {\lbrace 0, 1 \rbrace^*} \to \lbrace 0, 1 \rbrace^n$ be a collision resistant hash function. Consider the $(n+1)$-bit hash function $h$ defined as

$$
h(x) = \begin{cases}
1 \| x & \text{if $|x| = n$,} \\
0 \| g(x) & \text{otherwise.}
\end{cases}
$$

Show that $h$ is collision resistant, but not preimage resistant.

----

* Assume that $h$ is not collision resistant.
- We can efficiently find a collision $(x, x')$ such that $x \ne x'$ and $h(x) = h(x')$.
- If $h(x) = h(x') = 1 \Vert \hat{x}$, then $\hat{x} = x = x'$, contradiction.
- If $h(x) = h(x') = 0 \Vert \hat{x}$, then $\hat{x} = g(x) = g(x')$, so we have a collision for $g$, contradiction.
* Therefore, $h$ is collision resistant.
* For $y = 1 \Vert x$, then we have $h(x) = y$, i.e., $x$ is a preimage for $y$.
* Therefore, $h$ is not preimage resistant.

---

### Exercise 3

Suppose that ${H_1}, {H_2} : {\lbrace 0, 1 \rbrace^*} \to \lbrace 0, 1 \rbrace^n$ are collision resistant hash functions. Show that the function ${H_3}(x) = {H_2}({H_1}(x))$ is also collision resistant.

----

* Assume that ${H_3}$ is not collision resistant.
- We can efficiently find $(x, x')$ such that $x \ne x'$ and ${H_3}(x) = {H_3}(x')$.
- ${H_2}({H_1}(x)) = {H_2}({H_1}(x'))$
- If ${H_1}(x) = {H_1}(x')$, then $(x, x')$ is a collision for ${H_1}$, contradiction.
- Therefore, ${H_1}(x) \ne {H_1}(x')$.
- Then $({H_1}(x), {H_1}(x'))$ is a collision for ${H_2}$, contradiction.
* Therefore, ${H_3}$ is collision resistant.

---

### Exercise 4

Let $H : {\lbrace 0, 1 \rbrace^*} \to \lbrace 0, 1 \rbrace^n$ be a collision resistant hash function. Which of the following are collision resistant?

1. $H'(x) = H(x) \oplus H(x)$
2. $H'(x) = H(x \Vert 0)$
3. $H'(x) = H(x) \Vert H(0)$
4. $H'(x) = H(x)[0:31]$ (i.e., the first $32$ bits of the hash)
5. $H'(x) = H(x)[0:(n-2)]$ (i.e., the hash without the last bit)
6. $H'(x) = H(H(x))$
7. $H'(x) = H(H(H(x)))$
8. $H'(x) = H(0)$
9. <i>$H'(x) = H(x) \oplus H(x \oplus 1^{|x|})$</i> (where <i>$x \oplus 1^{|x|}$</i> is the bit-complement of $x$)

----

1. $H'(x) = 0$, trivially not collision resistant.
2. If $H'(x) = H'(x')$, then $H(x \Vert 0) = H(x' \Vert 0)$, and we have a collision $(x \Vert 0, x' \Vert 0)$ for $H$. Therefore, $H'$ is collision resistant.
3. Collision resistant (although the second half of the hash is constant).
4. By the birthday attack, we can find a collision in $O(2^{n'/2})$ time. Since $n' = 32$, this gives us $O(2^{16})$ computations - this can done efficiently, so $H'$ is not collision resistant.
5. Birthday attack on $H'$ possible in $O(2^{(n-1)/2})$, so about $\sqrt{2}$ times faster than for $H$.
6. Yes, by the argument of exercise 3 $({H_1} = {H_2} = H)$.
7. Yes, same argument.
8. Constant function, not collision resistant.
9. Given $x$, let <i>$x' = x \oplus 1^{|x|}$</i>. Then <i>$H'(x') = H(x \oplus 1^{|x|}) \oplus H(x) = H'(x)$</i>. Therefore, $H'$ is not second preimage resistant and thus also not collision resistant.

---

### Exercise 5 - multicollisions in iterated hash functions

Let $H$ be an iterated hash function with compression function $f : \lbrace 0, 1 \rbrace^{n+r} \to \lbrace 0, 1 \rbrace^n$. Suppose that you are given an algorithm $A$, which on input $z \in \lbrace 0, 1 \rbrace^n$ finds $s, t \in \lbrace 0, 1 \rbrace^r$, $s \ne t$, such that $f(z, s) = f(z, t)$. Let $T$ be the running time of $A$, and let $L = 2^\ell$, where $\ell$ is a positive integer. Show how $A$ can be used to find, in time $\ell T$, a collection of $L$ pairwise distinct messages ${x_1}, {x_2}, \dots, {x_L}$ such that $H({x_1}) = H({x_2}) = \dots = H({x_L})$.

----

z = IV
s, t = lists of length l
for i in range(l):
    s[i], t[i] = A(z)
    z = f(z, s[i])

* <i>${x_j} = {m_{j_1}^1}$</i><i>$\Vert {m_{j_2}^2}$</i><i>$\Vert \cdots \Vert {m_{j_\ell}^\ell}$</i>, where ${j_h}$ is the $h$-th bit of $j$, and
* $$
m^i_b = \begin{cases}
s[i] & b = 0 \\
t[i] & b = 1
\end{cases}
$$

---

### Exercise 6 - multiple hash functions

Prove that the concatenation of the $\operatorname{MD5}$ and $\operatorname{SHA-1}$ hash functions yields no appreciably greater security than $\operatorname{SHA-1}$ alone. More specifically, show that a collision can be found for the hash function $H : {\lbrace 0, 1 \rbrace^*} \to \lbrace 0, 1 \rbrace^{288}$ given by

$$
H(x) = \operatorname{MD5}(x) \| \operatorname{SHA-1}(x)
$$

using roughly $C \cdot 2^{80}$ operations, for some reasonably sized constant $C$.

----

* find a multicollision $M = \lbrace {x_1}, {x_2}, \dots, {x_L} \rbrace$ for $\operatorname{MD5}$ in $\ell \cdot 2^{64}$ time, such that $L = 2^\ell \approx C \cdot 2^{80}$, so $\ell \approx 80 \log_2{C}$
* perform a birthday attack on the set $M$ in $C \cdot 2^{80}$ time to obtain a collision $(x, x')$ for $\operatorname{SHA-1}$