# Exercice 1
Soit une porte d’amplitude 1, de 124 points sur sa partie haute et de 2 points de part et d’autre de celle-ci, d’amplitude 0. Vous disposez alors d’un signal de 128 points.
Afficher ce signal. Quelle fonction classique de traitement de signal avez-vous créée ?

% création du signal
signal = [zeros(1, 2), ones(1, 124), zeros(1, 2)];

% affichage du signal
plot(signal);
xlabel('Échantillons');
ylabel('Amplitude');
title('Signal');


% genérer le vecteur x de 0 à 127 par pas de 1
x = 0:127;

% generer le vecteur y en fonction de la parité 
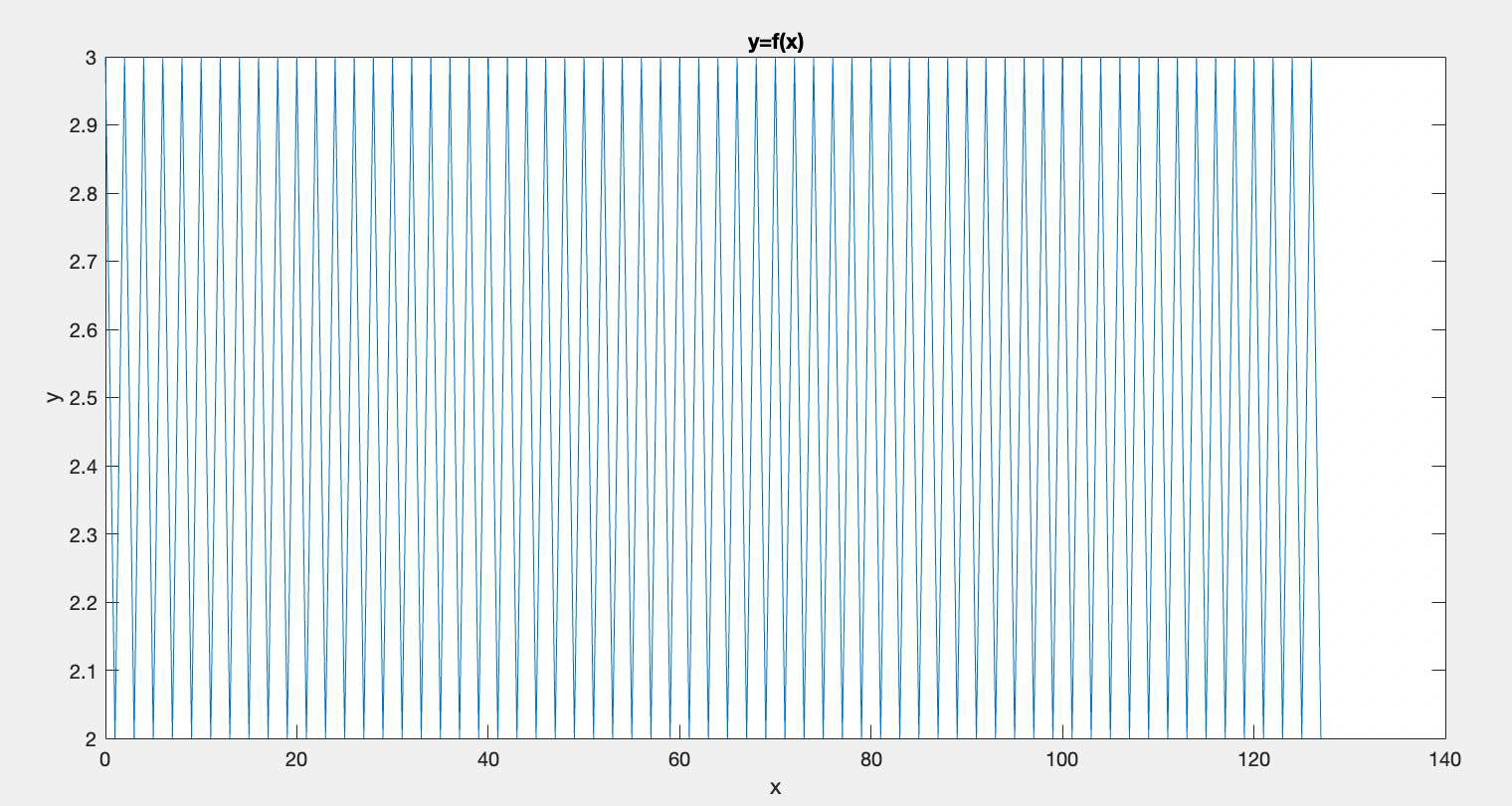
y = 2 + (mod(x, 2) == 0);  % Cela alternera correctement entre 2 et 3. 

% afficher le graphique de y en fonction de x
plot(x, y);
xlabel('x');
ylabel('y');
title('y=f(x)');


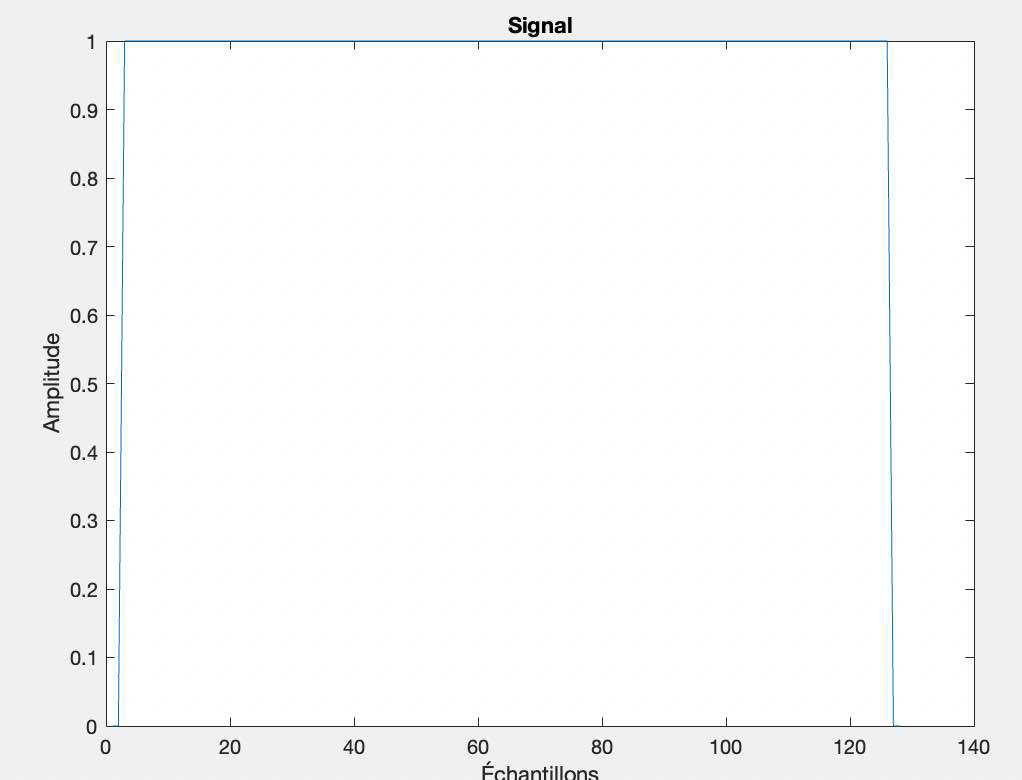
Nous avons créer filtre passe-bas : permet de passer toutes les fréquences en dessous d'une certaine fréquence de coupure tout en atténuant les fréquences supérieures

---

Générez un vecteur « x » allant de 0 à 127 par pas de 1.
Générer un vecteur « y » de longueur identique, qui contient 2 valeurs : 2 et 3 selon que l’indice du vecteur soit pair ou impaire. Afficher
y=f(x).


# Exercice 2

Générez un signal sinusoïdal de fréquence $5 \mathrm{~Hz}$ d'une durée de $1 \mathrm{~s}$. Echantillonnez à $10 \mathrm{~ms}$.

Quel est le temps total de ce signal ? Quels sont le temps et la fréquence d'échantillonnage ?
Affichez ce signal sinusoïdal. Attention à l'axe des abscisses.

duree = 1;              % durée en secondes
frequence = 5;          % fréquence ( Hz)
echantillonnage = 0.01; % intervalle d échantillonnage  (10 ms)

% calcul du nombre d echantillons
nombre_echantillons = duree / echantillonnage;

% generation du vecteur de temps
temps = linspace(0, duree, nombre_echantillons);

% generation du signal sinusoïdal
signal = sin(2 * pi * frequence * temps);

% affichage du signal 
plot(temps, signal);
xlabel('Temps en s');
ylabel('Amplitude');
title('Signal sinusoïdal de 5 Hz');


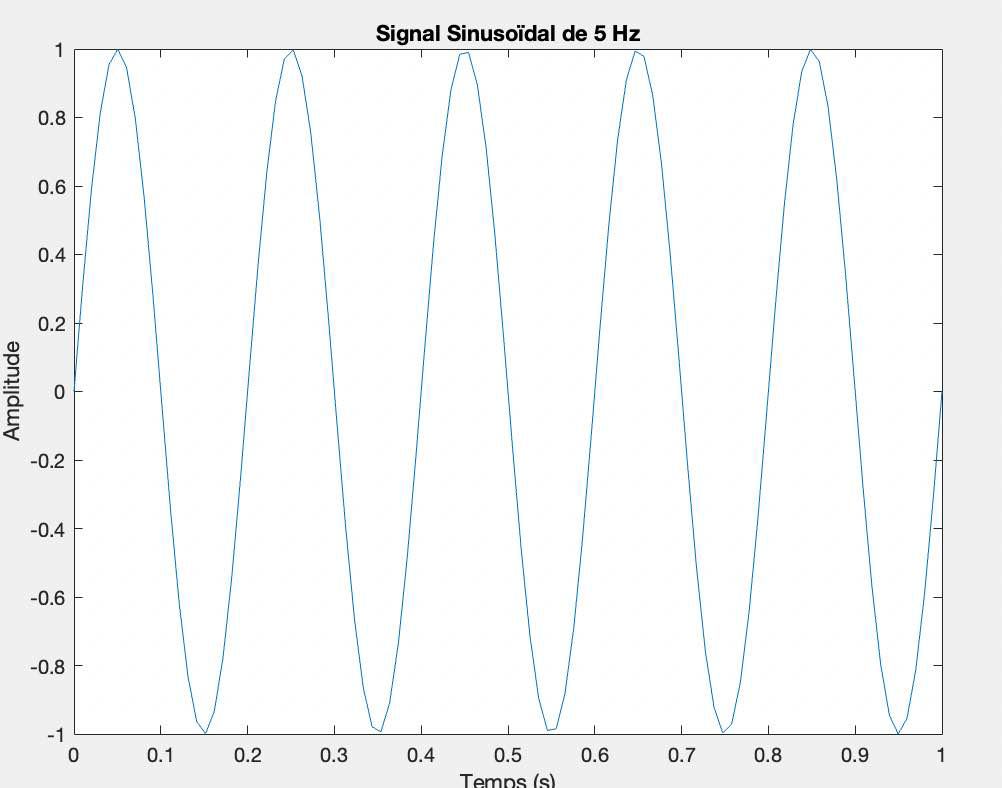
La durée du signal est définie comme duree = 1 seconde, et l'intervalle d'échantillonnage est défini comme echantillonnage = 0.01 seconde (10 ms).

Le temps total du signal est donc égal à la durée, soit 1 seconde.

La fréquence d'échantillonnage est l'inverse de l'intervalle d'échantillonnage ( 1 / 0.01 = 100 Hz).

# Exercice 3
Générez un sinus cardinal (fonction sinc) avec un axe fréquentiel allant de $\mathbf{- 1 0} \mathbf{H z}$ à $\mathbf{1 0} \mathbf{H z}$ par pas de $0.01 \mathrm{~Hz}$.

Affichez ce signal. Attention à l'axe des abscisses.
Quelle est la fréquence d'échantillonnage ? Quelle est la résolution fréquentielle?

> Il faut installer : Signal Processing Toolbox

% plage  fréquences de -10 Hz à 10 Hz par pas de 0,01 Hz
fre = -10:0.01:10;

% calculez la fonction sinc pour chaque fréquence
sinc_signal = sinc(fre);

% fréquence d'échantillonnage (résolution fréquentielle)
fre_echan = 1 / (0.01); 

% affichez le signal
figure;
plot(fre, sinc_signal);
xlabel('Fréquence (Hz)');
ylabel('Amplitude');
title('Sinus Cardinal (fonction sinc)');
grid on;

% affichez la fréquence d'échantillonnage
disp(['fréquence échantillonnage : ' num2str(fre_echan) ' Hz']);


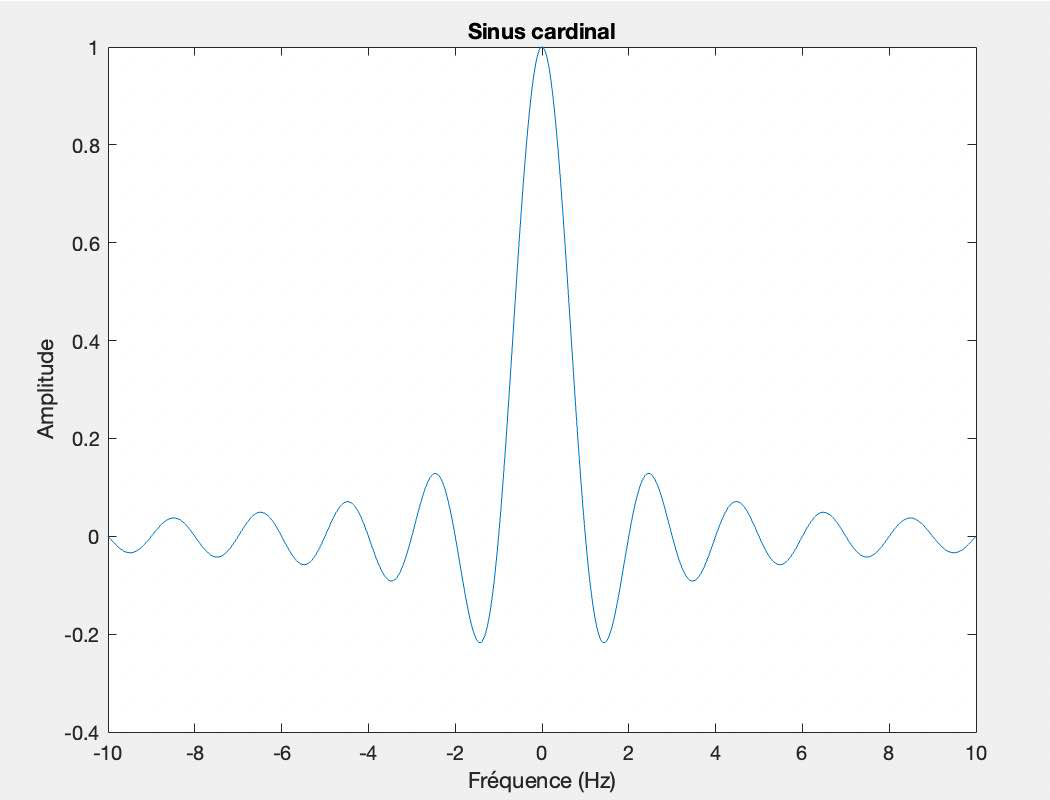
Fréquence d''échantillonnage : 1/Échantillonnage = 1/0,01 = 100 HZ

La résolution fréquentielle est également de 0,01 Hz, car nous avons utilisé un pas de 0,01 Hz pour la génération des fréquences.

# Exercice 4

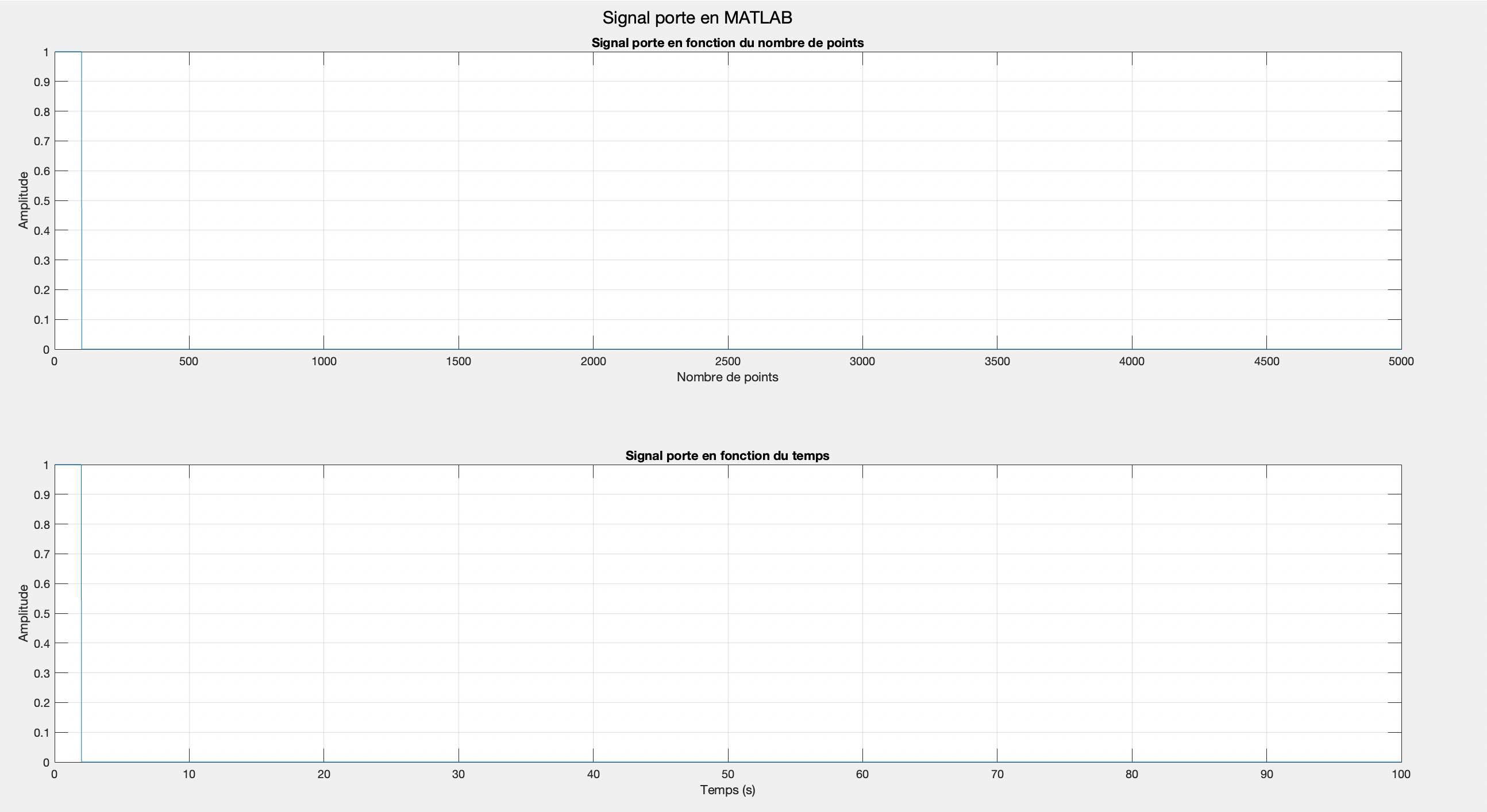
Générez une porte contenant 100 points d'amplitude 1,4900 points d'amplitude 0 , d'une durée totale de 100 s et d'un temps d'échantillonnage de $0.02 \mathrm{~s}$. Afficher ce signal en fonction du nombre de points. Affichez le même signal en fonction du temps.

Calculer la transformée de Fourier de ce signal.
Afficher cette transformée de Fourier en décimal et en décibel.

Quelle représentation est la plus adaptée?

duree_totale = 100; % durée totale (s)
temps_echantillonnage = 0.02; % temps d'échantillonnage (s)
nb_points_porte = 100; % nombre de points avec une amplitude de 1
amplitude_porte = 1; % amplitude du signal porte

% calcul du nombre total de points
nb_total_points = duree_totale / temps_echantillonnage;

% création du vecteur temps
temps = 0:temps_echantillonnage:(nb_total_points-1)*temps_echantillonnage;

signal = zeros(1, nb_total_points); % initialise le signal à zéro
signal(1:nb_points_porte) = amplitude_porte; % donne une amplitude de 1 aux premiers 100 points

% affichage en fonction du nombre de points
figure;
subplot(2, 1, 1);
plot(signal);
title('Signal porte en fonction du nombre de points');
xlabel('Nombre de points');
ylabel('Amplitude');
grid on;

% affichage en fonction du temps
subplot(2, 1, 2);
plot(temps, signal);
title('signal porte en fonction du temps');
xlabel('Temps (s)');
ylabel('Amplitude');
grid on;

sgtitle('signal porte en MATLAB');
set(gcf, 'Position', get(0, 'Screensize'));

% calcul de la transformée de Fourier
signal_fft = fft(signal);

% ajustement de l'amplitude de la FFT en raison de la longueur du signal
signal_fft = signal_fft / nb_total_points;

% calcul de la fréquence d'échantillonnage
frequence_echantillonnage = 1 / temps_echantillonnage;

% création du vecteur fréquence (hertz) ajusté pour la moitié positive des fréquences
frequence = (0:(nb_total_points/2)-1)*(frequence_echantillonnage/nb_total_points);

% préparation de la transformée de Fourier pour l'affichage (seulement la moitié positive)
signal_fft_half = signal_fft(1:nb_total_points/2);

% calcul de la puissance spectrale (en décibel)
puissance_spectrale_db = 20 * log10(abs(signal_fft_half));

% affichage de la transformée de Fourier en valeurs décimales
figure;
subplot(2, 1, 1);
plot(frequence, abs(signal_fft_half));
title('Transformée de Fourier (Valeurs décimales)');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');
grid on;

% affichage de la transformee de Fourier en décibel
subplot(2, 1, 2);
plot(frequence, puissance_spectrale_db);
title('Transformee de Fourier (dB)');
xlabel('Fréquence (Hz)');
ylabel('Puissance (dB)');
grid on;

sgtitle('Transformée de Fourier du signal porte');
set(gcf, 'Position', get(0, 'Screensize')); % plein écran

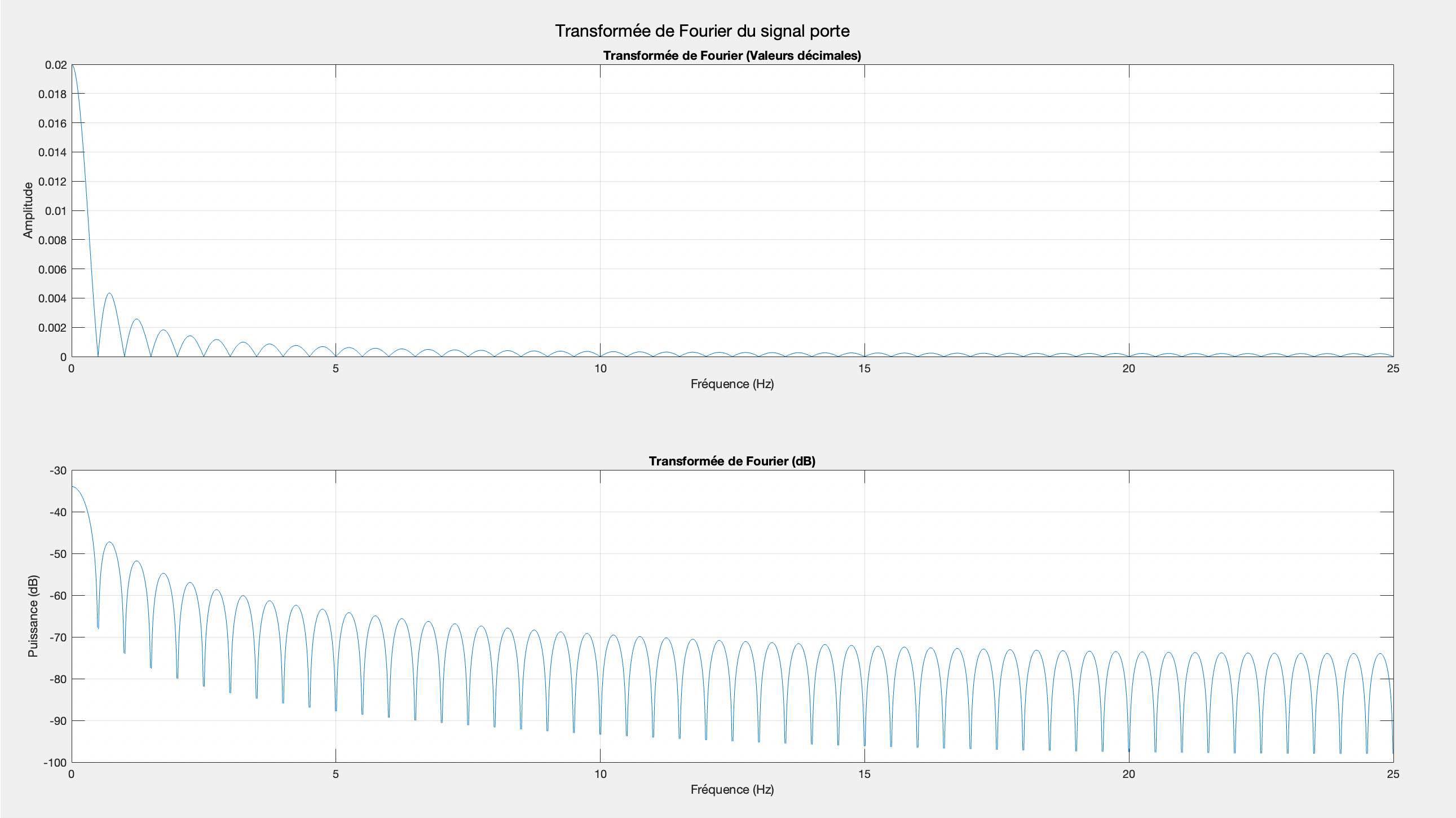
La representation sous forme décimal est plus adapté, car elle met en évidence les amplitudes brut des composantes de fréquence.

# Exercice 5
Reprendre le signal porte de l'exercice 4.

Afficher le spectre sur les intervalles $[0 ; \mathrm{fe}]$ et $[-\mathrm{fe} / 2 ; \mathrm{fe} / 2]$.

duree_totale = 100; % duree totale
temps_echantillonnage = 0.02; % temps deéchantillonnage
nb_points_porte = 100; % nombre de points avec une amplitude de 1
amplitude_porte = 1; % amplitude du signal porte

% Cclcul du nombre total de points
nb_total_points = duree_totale / temps_echantillonnage;

% création du vecteur temps
temps = 0:temps_echantillonnage:(nb_total_points-1)*temps_echantillonnage;

% init le signal à zéro
signal = zeros(1, nb_total_points);

% attribution d'une amplitude de 1 aux premiers 100 points
signal(1:nb_points_porte) = amplitude_porte;

% calcul de la transformée de Fourier du signal
signal_fft = fft(signal);

% normalisation de la FFT
signal_fft = signal_fft / nb_total_points;

% calcul de la fréquence dcéchantillonnage
frequence_echantillonnage = 1 / temps_echantillonnage;

% création du vecteur fréquence
frequence = (0:(nb_total_points/2)-1)*(frequence_echantillonnage/nb_total_points);

% preparation de la transformée de Fourier
signal_fft_half = signal_fft(1:nb_total_points/2);

% Décalage du spectre
signal_fft_shifted = fftshift(signal_fft);

% création du vecteur
frequence_shifted = (-nb_total_points/2:(nb_total_points/2)-1)*(frequence_echantillonnage/nb_total_points);

% Affichage
figure;
subplot(2, 1, 1);
plot(frequence, abs(signal_fft_half));
title('Spectre du signal porte [0; fe]');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');
grid on;

% Affichage
subplot(2, 1, 2);
plot(frequence_shifted, abs(signal_fft_shifted));
title('Spectre du signal porte [-fe/2; fe/2]');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');
grid on;

sgtitle('Spectre du signal porte avec et sans fftshift');
set(gcf, 'Position', get(0, 'Screensize')); % plein écran


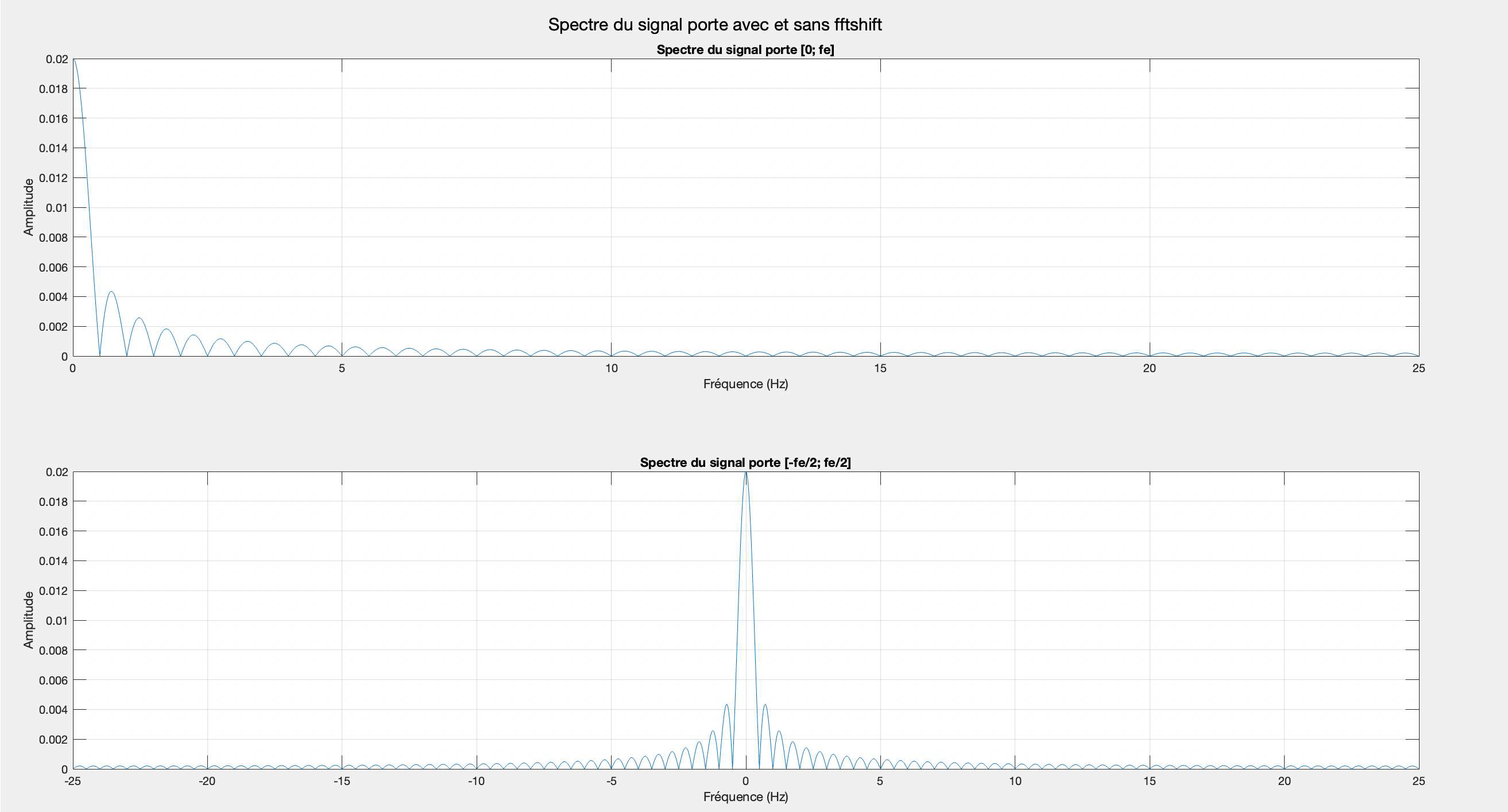
# Exercice 6

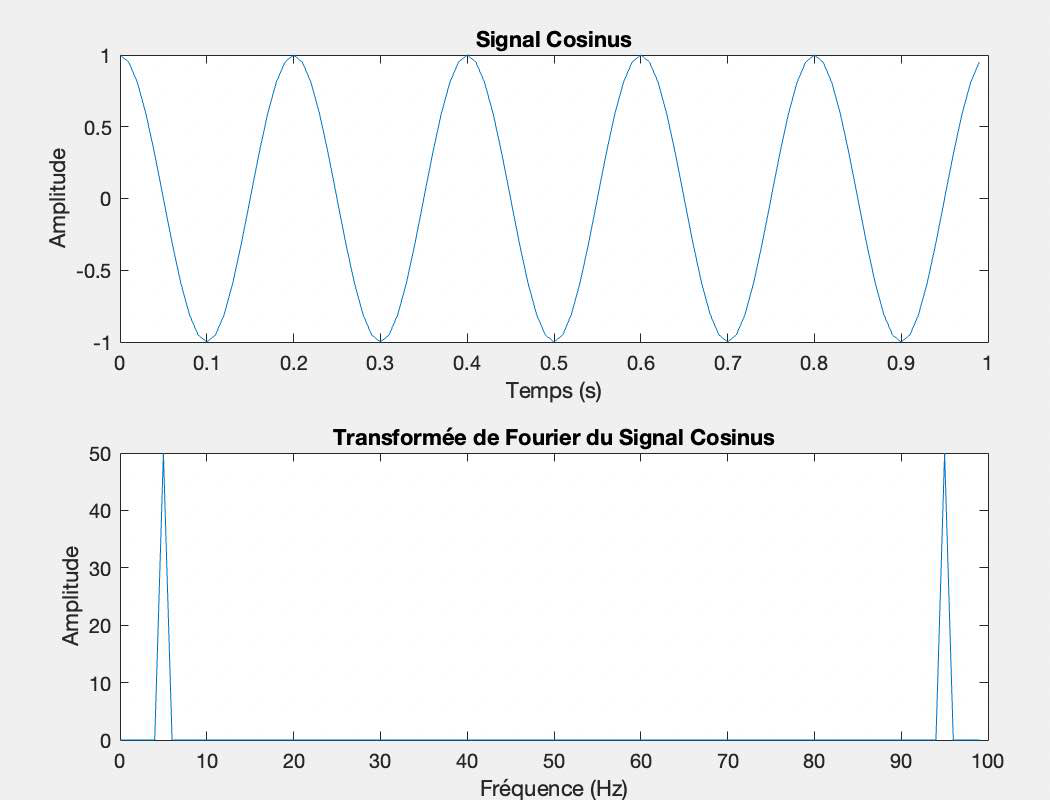
Soit y un signal sinusoïdal de fréquence $5 \mathrm{~Hz}$, d'une durée de $1 \mathrm{~s}$, et d'un temps d'échantillonnage de 0.01 s. Tracer y et sa transformée de Fourier. Faire de même avec un cosinus. Quel problème rencontrez-vous?

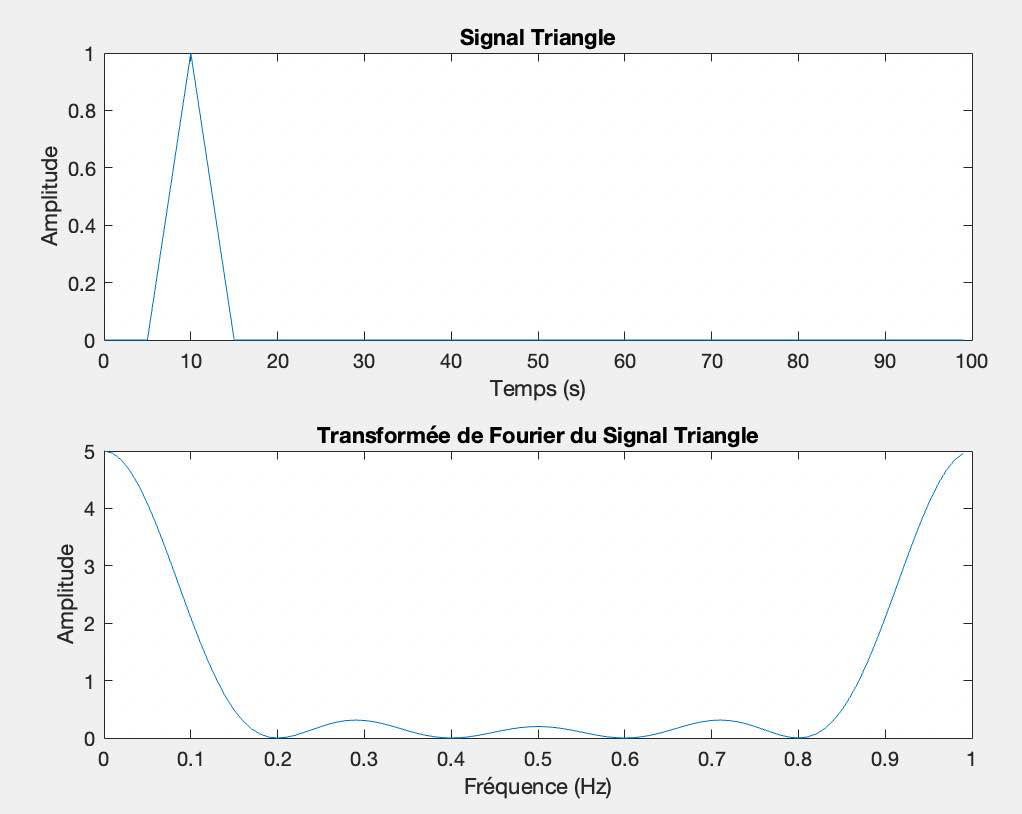
Soit y un signal triangle, centré en $\mathrm{T}=10 \mathrm{~s}$, de largeur $\mathrm{T}=10 \mathrm{~s}$. La durée totale de y doit être de $100 \mathrm{~s}$ avec un temps d'échantillonnage de 1s. Tracer y et sa transformée de Fourier.

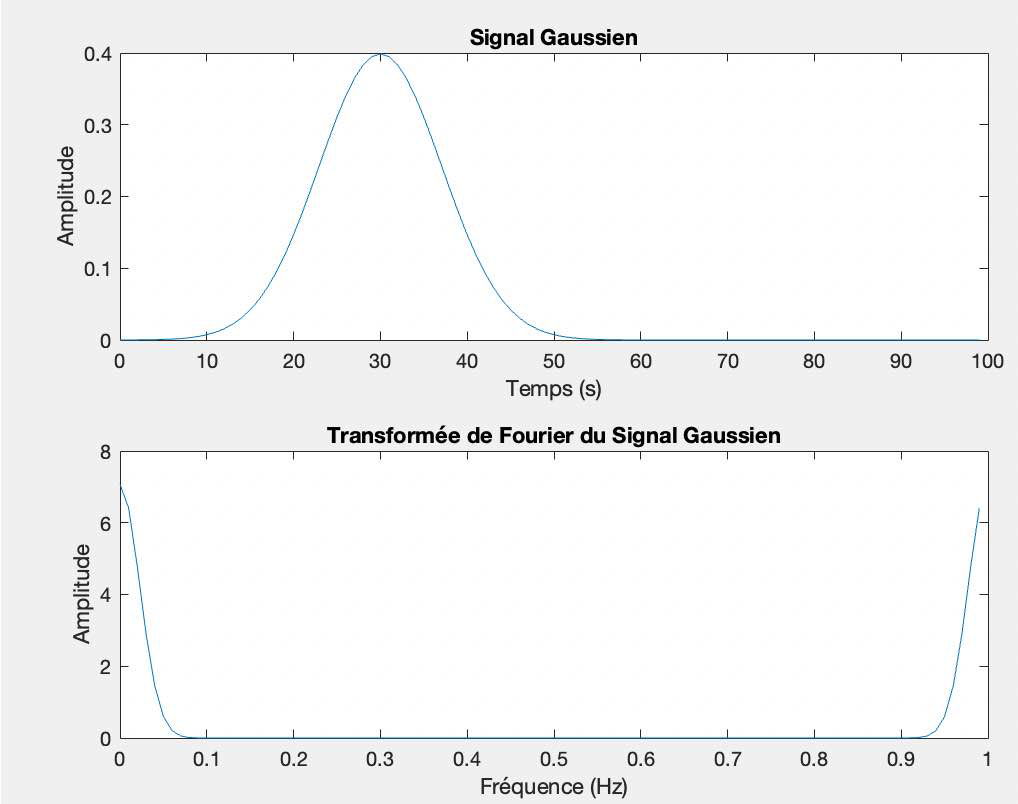
Soit y une gaussienne d'expression $y=\frac{1}{\sqrt{2 \pi}} \exp \left(-b . t^2\right)$. La durée de cette gaussienne est de 100 s, son temps d'échantillonnage de $1 \mathrm{~s}$. La gaussienne doit être centrée en $\mathrm{T}=30 \mathrm{~s}$. Pour le facteur $\mathrm{b}$ vous pouvez prendre la valeur $0.1^2$. Tracer y et sa transformée de Fourier.

frequence = 5;
duree = 1; 
Te = 0.01; 
t = 0:Te:duree-Te; 

% Signal sinusoïdal
y_sin = sin(2 * pi * frequence * t);
% Transformée de Fourier
Y_sin = fft(y_sin);
f_sin = (0:length(Y_sin)-1)*(1/duree); 

% Tracé du signal sinusoïdal et sa transformée de Fourier
figure; 
subplot(2,1,1);
plot(t, y_sin);
title('Signal Sinusoïdal');
xlabel('Temps (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(f_sin, abs(Y_sin)/length(y_sin));
title('Magnitude de la Transformée de Fourier du Signal Sinusoïdal');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');

% Signal cosinus
y_cos = cos(2 * pi * frequence * t);
% Transformée de Fourier
Y_cos = fft(y_cos);
f_cos = (0:length(Y_cos)-1)*(1/duree);

% Tracé du signal cosinus et sa transformée de Fourier
figure;
subplot(2,1,1);
plot(t, y_cos);
title('Signal Cosinus');
xlabel('Temps (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(f_cos, abs(Y_cos)/length(y_cos));
title('Magnitude de la Transformée de Fourier du Signal Cosinus');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');

% Signal triangle
duree_totale = 100; 
Te_triangle = 1; 
t_triangle = 0:Te_triangle:duree_totale-Te_triangle;
T = 10;
y_triangle = tripuls(t_triangle-T, T);

% Transformée de Fourier
Y_triangle = fft(y_triangle);
f_triangle = (0:length(Y_triangle)-1)*(1/duree_totale);

% Tracé du signal triangle et sa transformée de Fourier
figure;
subplot(2,1,1);
plot(t_triangle, y_triangle);
title('Signal Triangle');
xlabel('Temps (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(f_triangle, abs(Y_triangle)/length(y_triangle));
title('Magnitude de la Transformée de Fourier du Signal Triangle');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');

% Signal gaussien
duree_gauss = 100; 
Te_gauss = 1; 
t_gauss = 0:Te_gauss:duree_gauss-Te_gauss;
b = 0.1^2; 
T_gauss = 30;
y_gauss = (1/sqrt(2*pi*b)) * exp(-((t_gauss-T_gauss).^2)/(2*b));

% Transformée de Fourier
Y_gauss = fft(y_gauss);
f_gauss = (0:length(Y_gauss)-1)*(1/duree_gauss);

% Tracé du signal gaussien et sa transformée de Fourier
figure;
subplot(2,1,1);
plot(t_gauss, y_gauss);
title('Signal Gaussien');
xlabel('Temps (s)');
ylabel('Amplitude');

subplot(2,1,2);
plot(f_gauss, abs(Y_gauss)/length(y_gauss));
title('Magnitude de la Transformée de Fourier du Signal Gaussien');
xlabel('Fréquence (Hz)');
ylabel('Amplitude');

Fonction triangle recentree :-1:
% Préparation de l'environnement
clear; close all; clc;

% Paramètres du signal triangle
T_centre = 10; % Le signal est centré à 10 secondes
T_largeur = 10; % La largeur du triangle est de 10 secondes
duree_totale = 100; % Durée totale du signal
Te = 1; % Temps d'échantillonnage en secondes

% Création du vecteur temps
t = -duree_totale/2:Te:duree_totale/2-Te; % Vecteur temps centré autour de zéro

% Génération du signal triangle
% La fonction tripuls n'étant pas standard, on crée un signal triangle manuellement
triangle = @(t, width) max(1 - abs(t)/width, 0); % Fonction anonyme pour un triangle
y = triangle(t, T_largeur/2);

% Calcul de la transformée de Fourier
Y = fft(y);
Y_shifted = fftshift(Y); % Recentre la transformée de Fourier

% Fréquences associées, recentrées
N = length(y);
f_shifted = (-N/2:N/2-1)*(1/(Te*N)); % Vecteur de fréquences recentré

% Affichage du signal triangle
subplot(2,1,1);
plot(t + T_centre, y); % On rajoute T_centre pour centrer le signal à 10 secondes
title('Signal triangle');
xlabel('Temps (s)');
ylabel('Amplitude');

% Affichage de la transformée de Fourier du signal triangle, recentrée
subplot(2,1,2);
plot(f_shifted, abs(Y_shifted));
title('Transformée de Fourier du signal triangle (recentrée)');
xlabel('Fréquence (Hz)');
ylabel('Magnitude');

Signal de Gauss corrige :
% Préparation de l'environnement
clear; close all; clc;

% Paramètres de la gaussienne
b = 0.1^2; % Facteur b dans l'expression de la gaussienne
duree_totale = 100; % Durée totale du signal en secondes
Te = 1; % Temps d'échantillonnage en secondes
T_centre = 30; % La gaussienne est centrée à 30 secondes

% Création du vecteur temps
t = (0:Te:duree_totale-Te) - T_centre; % Vecteur temps centré sur la gaussienne

% Génération de la gaussienne
y = (1/(sqrt(2*pi))) * exp(-b * t.^2);

% Calcul de la transformée de Fourier
Y = fft(y);
Y_shifted = fftshift(Y); % Recentre la transformée de Fourier

% Fréquences associées, recentrées
N = length(y);
f_shifted = (-N/2:N/2-1)*(1/(Te*N)); % Vecteur de fréquences recentré

% Affichage de la gaussienne
subplot(2,1,1);
plot(t + T_centre, y); % On recentre le signal en temps pour l'affichage
title('Signal gaussien');
xlabel('Temps (s)');
ylabel('Amplitude');

% Affichage de la transformée de Fourier de la gaussienne, recentrée
subplot(2,1,2);
plot(f_shifted, abs(Y_shifted));
title('Transformée de Fourier du signal gaussien (recentrée)');
xlabel('Fréquence (Hz)');
ylabel('Magnitude');

% Ajustement de l'axe des fréquences pour se concentrer sur la partie principale
xlim([-1/Te 1/Te]);

L'amplitude et la phase de du signal de la transformée de fourier du cosinus et du sinus sont équivalent, car elles possèdent la même fréquence.