Parallelization of A* Search Algorithm
**By: William Foy (wfoy) and Jacob Zych (jzych)**
### Summary: ###
We will explore the performance differences of the A* search algorithm implemented in C++ both sequentially and in parallel. A* can be implemented in parallel using either a centralized data structure or decentralized data structures. Our project will explore the performance and solution optimality for these various parallelization techniques implemented using openMPI as well as in Golang to determine which yield the highest speedups.
### Background: ###
A* search is a graph traversal algorithm used to find the shortest path (using some heuristic function) between a source and target vertex. A* minimizes the path funtion `f(n)=g(n)+h(n)` where `g(n)` is the cost from the start node to node `n` and `h(n)` is the heuristic function estimating the cost from node `n` to the target node. This algorithm is typically implemented sequentially using priority queues and an algorithm similar to BFS.
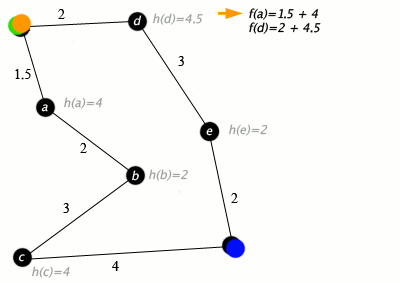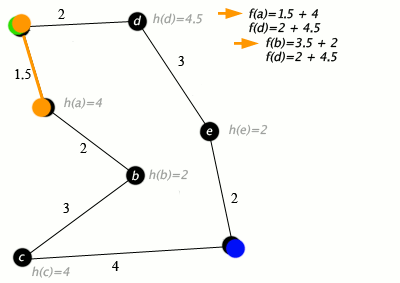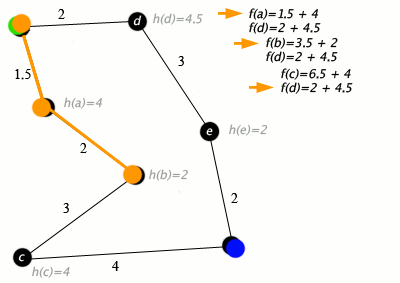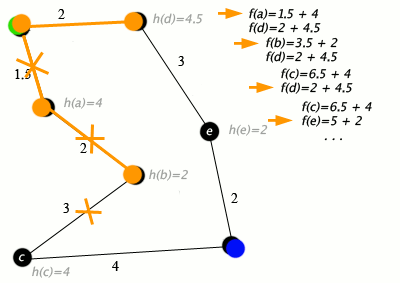
Our implementation of A* will be designed to work on grid based graphs where each element in the grid has up to 4 neighbors adjacent to them. This reason for this is that it doesn't really make sense to use A* on simple graphs because they do not benefit much from heuristic functions. For simple graphs, Dijkstra's algorithm would likely perform better.
We seek to implement A* sequentially and in parallel using two significantly different techniques.
The first, and arguably more simple approach, is centralized A* (or simple parallel A*). In this approach, all processors or threads operate on a single shared menory open set, or set of nodes that are currently being evaluated. Each thread expands one of the best nodes in the current open set and generates its children nodes, updating the shared open set. This approach can be severely bottlenecked by the shared global data structure, so in our results we expect to see this approach to parallelizing yielding the worst results. We will implement this approach using pthreads.
The second approach is decentralized A*. This approach offers a lower synchronization overhead than a shared memory approach. Here, a root processor distributes the work among other processors which each compute their local optimal solution. When neighbors are generated, they are sent to another processor's buffer. When a processor empties their working queue, they check for whether or not the algorithm should be terminated (i.e. whether or not their solution is globally optimal). In order to determine whether or not a solution is globally optimal, not only should all of the processors have empty working sets, there also must not be a message en route which may contain a better solution. In order to determine whether or not there is a message en route, we will use Mattern's time algorithm. We plan on implementing this decentralized version of the algorithm in C++ using openMPI as well as in Golang which uses goroutines (which are similar to lightweight threads that can pass messages to each other via channels).
Another interesting issue that arises when decentralizing A* is load balancing. The most simple solution to load balancing is to have processors send their expanded nodes to a random processor (or a processor operating on nodes close to the current processor's nodes). This results in a lot of overhead as processors must check whether or not the nodes they are receiving are duplicate nodes, which decreases the overall performance of the code.
In order to address this, we can assign a unique processor to each node by hashing the search space. Thus, each processor can only use their own local open set to check whether or not a node is a duplicate, reducing the overhead. We plan on implementing the Zobrist hash function which is defined as follows:
For simplicity, assume that s is represented as an array of n propositions, s = (x0, x1, ..., xn). Let R be a
table containing preinitialized random bit strings:
`Z(s) := R[x_0] xor R[x_1] xor · · · xor R[x_n]`.
There are other methods to hashing which we may explore depending on the performance and time remaining.
Ideally, the heuristic function chosen is fast and scalable. To make use of less precise heuristics, our implementation of A* will most likely be designed to work on grid based graphs. We will start by using Manhatten distance as the heuristic which computes the absolute distance between two nodes on the x and y axis and sums them. Since there is a tradeoff between speed and accuracy, we will test other heuristics to find the one that yields the best performance with the smallest impact on the optimality of the solution generated.
Below is some high level pseudocode of the A* search algorithm:
```
def search(G, source, target):
# initialize data structures
while openSet is not empty:
# get the current node
if current node equals the target:
return the best path
for each neighbor of the current node:
# calculate the path cost f(n) between the current node and the neighbor
# add the node yielding the best path cost to the frontier
```
Our final report will consist of performance graphs for each of the implementations, also considering how the type of graph (size, number of obstacles) impacts the accuracy and perfomance of the implementation. We will analyze which frameworks and variants are best depending on the type of application and why this might be the case.
If time permits, we will also attempt to implement A* using the domain-specific language GraphLab and compare its performance to our other implementations.
### Challenges: ###
* Decentralized Work Distribution
* We need to find the best way to distribute work among the processors to decrease overhead in detecting duplicate nodes
* Termination Detection
* Termination detection in decentralized A* is difficult to implement correctly
### Resources: ###
We plan on referencing some existing C++ implementations of the A* algorithms to help us familiarize ourselves with the sequential implementation.
We will use both pthreads and OpenMPI to parallelize the algorithm. We would also like to implement decentralized A* in golang using goroutines which can pass messages to each other over channels. We may also use GraphLab at the end as a stretch goal if time allows.
Our hardware for testing will consist of:
* GHC Machines (Intel(R) Core(TM) i7-9700 CPU @ 3.00GHz, 8 cores)
* PSC Machines - Regular Memory (2 AMD EPYC 7742 CPUs @ 2.25-3.40 GHz, 64 cores)
### Goals and Deliverables: ###
* *75%*
* Working sequential implementation of A*
* Working parallel implementation of centralized A* using pthreads
* Working parallel implementation of decentralized A* using openMPI
* *100%*
* 75% goals
* working implementation of A* in Golang using goroutines
* Graphs and Metrics comparing the implementations, parallel framework, fine tuning, graph size, and hardware
* *125%*
* 100% goals
* Working GraphLab implementation
* Animation showing graph algorithms in action
### Schedule: ###
| Days | Goal |
| --------- | --------|
| 4/18 | Finish entire sequential implemenation of A* |
| 4/19-4/20 | Finish simple parallel implementation of A* using pthreads |
| 4/21-4/24 | Finish decentralized A* using openMPI |
| 4/25-4/27 | Finish Golang implementation of decentralized A* |
| 4/28-4/29 | Performance measurements and report compilation
### References: ###
* https://en.wikipedia.org/wiki/A*_search_algorithm
* https://vs.inf.ethz.ch/publ/papers/mattern-dc-1987.pdf
* https://arxiv.org/pdf/1708.05296.pdf
### MILESTONE: ###
So far we have attempted to get a sequential version working of our original proposal with delaunay triangulation but with no success. The algorithm is too complex and we haven't had time to understand it and write our own implementation, and we also struggled to come up with tangible ways to parallelize the reference code we found. Because of these struggles, we chose to come up with a new idea that seemed more feasible.
Our new project focus is on parallelizing different implementations of the A* graph traversal algorithm using different frameworks and hardware and comparing the results. We think that this is an interesting problem space which can be completed in the remaining time left. We can also learn to use GraphLab in the later weeks if time allows. So far we have worked on formulating this new idea and getting sequential implementations up and running. We are still in the process of setting our build environment up and writing the sequential implementations for front-to-front and front-to-back.
The deliverables and new schedule seem much more doable than those in our previous proposal. We underestimated how difficult the sequential Delaumnay triangulation would be, but A* seems easier and the focus can be on parallelization.
At the poster session we plan to show graphs comparing the speedups for different configurations (implementation, framework, hardware). We might also have an animation showing how the graph traversal works if possible. We don't have any preliminary results at this time.
Currently the biggest concern is sitting down and doing the work. Our plan seems solid and the plan seems very feasible and interesting. So far both of us have not been able to dedicate the time we intended to this project due to other classes and commitments, but going forward we will each have more time to focus on this project.
 Sign in with Wallet
Sign in with Wallet

