# Mdm :(((
## liczenie i zliczanie
### Symbole asymptotyczne potrzebne zaleznosci
- $f(n) = O(g(x)) \iff \exists c > 0 \ \ \ \ |f(x)| \le c \cdot |g(x)|$
- $f(n) = \Omega(g(x)) \iff \exists c > 0 \ \ \ \ |f(x)| \ge c \cdot |g(x)|$
- $f(n) = \Theta(g(n)) \iff \exists c, d > 0 \ \ \ \ c \cdot |g(x)| \le |f(x)| \le d \cdot g(n)$
- $f(n) \sim g(n) \iff \frac{f(n)}{g(n)} \xrightarrow{n \rightarrow \infty} 1$
- $f(n) = o(g(n)) \iff \frac{f(n)}{g(n)} \xrightarrow{n \rightarrow \infty} 0$
### Zliczanie
- $n^k$ - liczba ciągów $i_1, i_2, ..., i_n$ gdzie $i_j \in \{1, 2, ..., n\}$
- $n^{\underline{k}}$ - i wyrazy się nie powtarzają. $\frac{n!}{(n-k)!}$
- $\binom{n}{k}$ - liczba k-elementowych podzbiorów {1, 2, ..., n}
- $\binom{n}{n_1, n_2, ..., n_k}$ - liczba ciągów złożonych z $n_1$ jedynek, $n_2$ dwójek, ... $n_k$ symboli, gdzie $n = n_1 + n_2 + ... + n_k$

### liczby Fibonacciego

$F_{m+n}=F_{n+1}F_{m}+F_{n}F_{m-1}$

### Chińskie twierdzenie o resztach

### Rozszerzony Euklides

liczba a ma odwrotność modularna w Zn <=> NWD(a, n) = 1

### Funkcja Eulera

jeżeli p jest liczbą pierwszą, to $\phi(p^{k})=p^{k-1}\cdot (p-1)$

Jeżeli $p_{1},p_{2},\dots ,p_{k}$ są wszystkimi czynnikami pierwszymi liczby n liczonymi bez powtórzeń, to

$\varphi (n)=n\left(1-{\tfrac {1}{p_{1}}}\right)\left(1-{\tfrac {1}{p_{2}}}\right)\dots \left(1-{\tfrac {1}{p_{k}}}\right)$

### Zasada szufladkowa

n szufladek, kn + 1 kulek -> w pewnej szufladce jest przynajmniej k + 1 kulek

### wzór dwumianowy

$(x+y)^{n}=\sum _{k=0}^{n}{\binom {n}{k}}x^{n-k}y^{k}$

$\binom{n}{k}= \binom{n - 1}{k} + \binom{n-1}{k-1}$

### zasada włączania i wyłączania

${\begin{aligned}\left|\bigcup _{i=1}^{n}A_{i}\right|&=\sum _{i=1}^{n}\left|A_{i}\right|-\sum _{i,j:\,i<j}\left|A_{i}\cap A_{j}\right|\\&+\sum _{i,j,k:\,i<j<k}\left|A_{i}\cap A_{j}\cap A_{k}\right|-\ \dots +(-1)^{n-1}\left|A_{1}\cap \cdots \cap A_{n}\right|,\end{aligned}}$

## grupy

### Twierdzienie Lagrange'a
czyli moc grupy = stabilizatory * orbity

#### Bézout’s Identity
If a and b are integers, then there exist integers x,y such that ax+by=gcd(a,b).

#### losowy lemat w temacie
If (x’,y’) is a solution to ax’+by’=n, then (x’-kb, y’+ka) is also a solution for any integer k.

#### liczby harmoniczne

### lemat Burnside'a
na chlopski rozum: wyznaczamy sobie ile jest mozliwych dzialan, liczymy ile obiektow generuje kazde dzialanie, sumujemy i dzielimy przez liczbe dzialan.


### funkcje tworzące

$A(x) = \sum{a_n\cdot x^n}$

wykladnicza:
$A(x) = \sum{\frac{a_n\cdot x^n}{n!}}$


### liczby Catalana

$C_{n}={\frac {1}{n+1}}{2n \choose n}={\frac {(2n)!}{(n+1)!\,n!}}=\prod \limits _{k=2}^{n}{\frac {n+k}{k}}\qquad {\text{for }}n\geq 0$

The first Catalan numbers for n = 0, 1, 2, 3, ... are $1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, ...$

recurrence relations:

$C_{0}=1\quad {\text{and}}\quad C_{n+1}=\sum _{i=0}^{n}C_{i}C_{n-i}\quad {\text{for }}n\geq 0$

and

$C_{0}=1\quad {\text{and}}\quad C_{n+1}={\frac {2(2n+1)}{n+2}}C_{n}$
::: spoiler
applications:
- Cn is the number of Dyck words[2] of length 2n. A Dyck word is a string consisting of n X's and n Y's such that no initial segment of the string has more Y's than X's. For example, the following are the Dyck words of length 6: XXXYYY XYXXYY XYXYXY XXYYXY XXYXYY.

- Re-interpreting the symbol X as an open parenthesis and Y as a close parenthesis, Cn counts the number of expressions containing n pairs of parentheses which are correctly matched: ((())) ()(()) ()()() (())() (()())

- Cn is the number of different ways n + 1 factors can be completely parenthesized (or the number of ways of associating n applications of a binary operator, as in the matrix chain multiplication problem). For n = 3, for example, we have the following five different parenthesizations of four factors: ((ab)c)d (a(bc))d (ab)(cd) a((bc)d) a(b(cd))

- Successive applications of a binary operator can be represented in terms of a full binary tree, with each correctly matched bracketing describing an internal node. It follows that Cn is the number of full binary trees with n + 1 leaves, or, equivalently, with a total of n internal nodes:
:::

### problem wydawania reszty

$P(x) = \prod _{i=0} ^{\infty} \frac{1}{1 - x^i}$

### liczby Stirlinga
$\begin{bmatrix} n \cr k \end{bmatrix}$ liczba sposobów na rozmieszczenie n liczb w k cyklach.

$\begin{bmatrix} n \cr n \end{bmatrix} = 1$, $\begin{bmatrix} n \cr 0 \end{bmatrix} = 0$, $\begin{bmatrix} 0 \cr 0 \end{bmatrix} = 1$.

$\begin{bmatrix} n \cr k \end{bmatrix}
= (n-1) \begin{bmatrix} n - 1 \cr k \end{bmatrix} +
\begin{bmatrix} n - 1 \cr k - 1\end{bmatrix}$

## Grafy

V – zbiór wierzchołków
E – zbiór krawędzi
S – zbiór ścian
n = |V|, m = |E|

**Stopień wierzchołka** v w grafie G to liczba krawędzi incydentnych z v. Stopień wierzchołka v oznaczany jest jako deg(v).

$∑ deg (v)=2|E|$.
d(G) > 2 i G regularny => d(G') <= 2

**Marszruta** to skończony ciąg krawędzi. Długość marszruty to liczba jej krawędzi. Marszruta zamknięta to marszruta kończąca się w punkcie wyjścia.

**Droga** to marszruta bez powtarzających się wierzchołków. Droga nazywana jest też często **ścieżką**.

**Cykl** to marszruta zamknięta, w której jedynym powtarzającym się wierzchołkiem jest jej początek.

Graf **spójny** to graf, w którym między dwoma dowolnymi wierzchołkami istnieje droga.

**Spójna składowa** grafu G=(V,E)
to maksymalny (w sensie inkluzji) podgraf spójny G.

usunięcie **wierzchołka rozcinającego** (grafu spójnego) rozspójnia graf

**Most** to krawędź, której usunięcie rozspójnia graf.

**Średnica** nazywamy maksymalną odległość między wierzchołkami grafu, to znaczy $d(G) = max\{d(x, y)|x, y ∈ V (G)\}$.

Maksymalna odległość od v :
$r(v) = max\{d(v, u)|u ∈ V (G)\}$

Wierzchołek $x_0$, dla którego $r(x_0) = min\{r(v)|v ∈ V (G)\}$ nazywamy **wierzchołkiem centralnym**, a liczbę $r(G) = r(x_0)$ **promieniem** grafu G.

**Skojarzenie** – podzbiór krawędzi grafu M o tej własności, że każdy wierzchołek jest końcem co najwyżej jednej krawędzi z M.

**Pokrycie wierzchołkowe** grafu G – taki podzbiór jego wierzchołków, że każda krawędź G jest incydentna do jakiegoś wierzchołka z tego podzbioru.

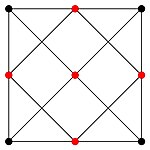
#### König-Egeváry
Dla dwudzielnych, największe skojarzenie ma moc najmniejszego pokrycia wierzchołkowego

### Drzewo
**Drzewo** to graf spójny nie zawierający cykli.

**Liść** drzewa to wierzchołek o stopniu 1.

Każde drzewo ma liść, każde drzewo o co najmniej 2 wierzchołkach ma przynajmniej 2 liście.

**Drzewo rozpinające** grafu G to podgraf grafu G zawierający wszystkie jego wierzchołki i będący drzewem.


Dla grafu $T=(V,E)$ następujące warunki są równoważne:

- T jest drzewem,
- T nie zawiera cykli i ma |V|−1 krawędzi,
- T jest spójny i ma |V|−1 krawędzi,
- T jest spójny, zaś usunięcie dowolnej krawędzi tworzy dokładnie dwie składowe,
- dowolne dwa wierzchołki grafu T są połączone dokładnie jedną drogą,
- T nie zawiera cykli, lecz dodanie dowolnej nowej krawędzi tworzy dokładnie jeden cykl,
- T jest spójny i każda krawędź jest mostem.

Drzew o zbiorze wierzchołków {1, 2, ..., n} jest $n^{n - 2}$

### Rodzaje

graf prosty - bez pętli i krawędzi wielokrotnych

Graf **pusty**, Antyklika lub graf niezależny - graf bez krawędzi ($A_n$).

Graf **pełny**, **klika** - graf, w którym każde dwa wierzchołki połączone są krawędzią ($K_n$). Liczba krawędzi w klice $K_n$ wynosi $\frac{n(n−1)}{2}$.

Graf **dwudzielny** to graf G=(V,E), w którym zbiór V da się podzielić na dwa rozłączne podzbiory V1 oraz V2 tak, by żadne dwa wierzchołki w obrębie tego samego podzbioru Vi nie były sąsiadami (V1 i V2 są **niezależne**).

Graf jest dwudzielny wtedy i tylko wtedy, gdy każdy jego cykl ma parzystą długość.

**Cykl Eulera** to zamknięta marszruta przechodząca przez każdą krawędź grafu dokładnie raz. Graf eulerowski to graf posiadający cykl Eulera.
Graf jest eulerowski wtedy i tylko wtedy, gdy jest spójny i stopień każdego wierzchołka jest parzysty.

**Cykl Hamiltona** to cykl przechodzący przez wszystkie wierzchołki grafu.
Graf hamiltonowski to graf posiadający cykl Hamiltona.
Ścieżka Hamiltona to ścieżka przechodząca przez wszystkie wierzchołki, każdy odwiedzając jedynie jeden raz.

#### twierdzenie Orego

Jeśli w grafie prostym $G=(V,E)$ o co najmniej 3 wierzchołkach dowolne dwa niesąsiednie wierzchołki v i w spełniają $deg(v)+deg(w)≥|V|$, to graf G jest hamiltonowski.

#### twierdzenie Diraca

Graf prosty $G=(V,E)$, w którym każdy wierzchołek ma stopień co najmniej $|V|/2$ jest hamiltonowski.

### Sieć
**Sieć** to trójka N=(V,A,c), w której:

- $(V,A)$ jest pełnym digrafem,
- funkcja $c:E⟶[0,+∞)$, zwana przepustowością sieci, każdej krawędzi vw przypisuje nieujemną liczbę rzeczywistą $c(vw)$.
- Wyróżnia się dwa wierzchołki $s,t∈V$, które są odpowiednio źródłem oraz ujściem sieci.

**Przepustowość** $c(vw)$ krawędzi vw może być interpretowana jako wartość potencjalnie maksymalnego przepływu z wierzchołka v do w.

**Przepływ** w sieci $N=(V,A,c)$ to funkcja $f:E⟶[0,+∞)$ spełniająca warunki:
- $0≤f(vw)≤c(vw)$ dla każdej krawędzi vw. (Wartość przepływu daną krawędzią nie może przekroczyć przepustowości tej krawędzi).
- $∑f(xv)=∑f(vx)$ dla każdego wierzchołka v poza źródłem s i ujściem t. (sumaryczna wartość tego, co wpływa do wierzchołka jest równa sumarycznej wartości tego, co zeń wypływa).
- $∑x∈V(f(sx)−f(xs))=∑x∈V(f(xt)−f(tx))$. (sumaryczna wartość tego, co wypływa ze źródła musi być równa sumarycznej wartości tego, co wpływa do ujścia. Wartość ta będzie określana wartością przepływu f).

**Przekrój** sieci to para podzbiorów (S,T) zbioru wierzchołków V, taka że:
- S,T tworzą podział V, tzn. są rozłączne i w sumie dają cały zbiór V,
- źródło s należy do S, a ujście t należy do zbioru T.

Przepustowość przekroju (S,T) to suma $c(S,T)=\sum _{v\in S, w∈T} c(vw)$.

W dowolnej sieci wartość maksymalnego przepływu jest równa przepustowości minimalnego przekroju.

### Graf Planarny
**graf planarny** - graf, który można narysować na płaszczyźnie tak, by krzywe obrazujące krawędzie grafu nie przecinały się ze sobą.

**ściany** - Dowolny rysunek płaski grafu planarnego wyznacza spójne obszary płaszczyzny zwane ścianami.

Jeżeli |V| ⩾ 3 oraz G jest grafem spójnym i planarnym, to |V| + |S| − |E| = 2.

Jeżeli |V| ⩾ 3 oraz G jest grafem planarnym, to $|E| \le 3 \cdot |V| - 6$ .

Jeżeli |V| ⩾ 3, nie ma trójkątów oraz G jest grafem planarnym, to $|E| \le 2 \cdot |V| - 4$ .

Dwa minimalne grafy, które **nie** są planarne, to $K_5$ i $K_{3,3}$.

**Kryterium Kuratowskiego** - graf skończony jest planarny $\iff$ nie zawiera podgrafu homeomorficznego z grafem $K_5$ ani z grafem $K_{3,3}$.

Dwa grafy $G_{1}$ i $G_{2}$ są **homeomorficzne**, jeśli można je oba otrzymać z pewnego grafu $G$ przez zastępowanie krawędzi grafu łańcuchami prostymi.

### Kolorowanie

**Kolorowanie** grafu $G=(V,E)$ to funkcja $c:V⟶N$ taka, że $c(v)≠c(w)$, jeśli vw jest krawędzią grafu $G$.

**Liczba chromatyczna** grafu, $χ(G)$, to najmniejsza liczba barw, którymi można pokolorować wierzchołki grafu $G$.

Graf, którego wszystkie wierzchołki mają stopień nie większy niż $k$ jest $(k+1)$-kolorowalny.

Graf dwudzielny wtedy $\iff$ 2-kolorowalny.

Każdy graf planarny jest 4-kolorowalny.

k to rozmiar największego zbioru niezależnego $\chi (G) \ge \frac{n}{k}$

$\chi(G) + \chi(\overline{G}) \le n+ 1$

Every k-chromatic graph has a k-chromatic subgraph of min degree at least k−1.

#### twierdzenie Brooksa
graf spójny:
- klika lub cykl nieparzysty $\chi(G) \le \Delta(G) + 1$
- w p. p. $\chi(G) \le \Delta(G)$

**index chromatyczny** minimalna liczba kolorów do kolorowania **krawędzi**

$\chi '(G) \ge deg(G)$
$\chi '(G) \le deg(G) + 1$

#### twierdzenie Kőniga
dla dwudzielnego $\chi'(G)=deg(G)$

#### Twierdzenie Hall'a

każdy podzbiór dziewcząt mocy k zna przynajmniej k chłopców => istnieje pełne skojarzenie

:::spoiler
Mamy dwie grupy – dziewcząt i chłopców – oraz pewną sieć znajomości, to znaczy wiemy, których chłopców z tej grupy zna każda z dziewczyn. Kiedy zachodzi sytuacja, w której każdej dziewczynie można przyporządkować jednego kandydata na męża? Tacy kandydaci nie mogą się powtarzać.

Rozwiązanie tak postawionego problemu nosi nazwę twierdzenia o kojarzeniu małżeństw.

Okazuje się, że warunkiem koniecznym i warunkiem wystarczającym na to, by istniało takie skojarzenie par, jest to, by każda podgrupa dziewcząt licząca k osób znała co najmniej k chłopców.
:::

#### twierdzenie Berge'a

M jest najliczniejszym skojarzeniem w grafie G $\iff$ G nie zawiera ścieżki powiększającej względem M.

## przyklady zadan
### wlaczenia i wylaczenia

### asymptotyka
czyli nieprawda ze f(n) ~ g(n)
zostaje to O i teta

### Burnside
https://www.quora.com/How-many-ways-is-it-possible-to-color-a-tetrahedron-using-k-colors-up-to-rotational-symmetry/answer/Richard-Goldstone?ch=15&oid=329188711&share=f7a42d14&target_type=answer

### szufladki
Podzielmy sobie nasz X na szufladki, takie że k-ta każda zawiera (2k + 1) * 2^i (k = 0, 1, ..., n-1). Istnieje szufladka, w której są conajmniej 2 elementy i elementy z jednej szufladki dzielą się przez siebie.

::: spoiler zly kuba
**Rozważmy podzbiory zbioru $S = {1,2,…,2n}$
Wykaż że jeżeli $X \subseteq S$ oraz $|X| \geq n$, to $X$ zawiera dwa różne elementy takie, że jeden z
nich dzieli drugi, tj. $a<b \land a|b$.**
Na początek rozważmy sytuacje gdy $1 \in X$ wtedy dla dowolnej liczby w zbiorze $X$ zachodzi teza. Rozpatrzmy teraz wszystkie takie zbiory $X$, które nie zawierają jedynki. Nasze szufladki podzielą zbiór $S$ w następujący sposób: weż liczbę $k\in{1,2,…,n}$ i jej dwukrotność (to będzie eykietka szuflady). Teraz bierzemy kolejne elementy zbioru $X$ i wkładamy je do szufladek gdzie na etykiecie ten element występuje. Skoro $|X|$ jest większa od $n$ oraz mamy $n$ szufladek to korzystając z zasady szufladkowej wynika nam że jakieś dwa elementy trafią do jednej szufladki. W tej szufladzie będzie element $k$ oraz $2k$. Zauważmy że $k|2k$. Co było do udowodnienia.
**Wskaż przykład takiego zbioru $X\subseteq S$ o mocy $n$, że dla każdych dwóch $a,b \in X$, takich, że $a<b$ i $a\nmid b$.**
Konstrukcja: Weżmy ostatnie $n$-elementów zbioru $S$. Dowód tego że żadne dwa elementy się w nim nie dzielą:
Weźmy dowolne dwie liczby z tak utworzonego zbioru $X$, jeśli którakolwiek z nich jest liczbą pierwszą to wtedy się nie dzielą ponieważ: jeśli $a$ jest to liczbą piewszą i jest wieksza od $n$ zatem jej "najbliższa" wielokrotność to jest liczba większa bądź równa $2n+2$ zatem jest spoza zbioru $X$. Natomiast jeśli $b$ jest liczbą pierwszą to żadna liczba poniżej niej jej nie dzieli ani nie jest jej wielokrotnością. (Zauważmy że zbiór $X$ nigdy nie zawiera liczby $1$).
Rozpatrzmy teraz sytuacje gdy żadna z nich nie jest liczbą pierwszą. To mamy dwa przypadki, albo $\gcd(a,b) = 1$ wtedy oczywiście $a\nmid b$, albo gdy $\gcd(a,b) > 1$. W przypadku tej drugiej, niech $c = \gcd(a,b)$, obserwacja jeśli $c$ byłoby większe od $n$ wtedy $a$ oraz $b$ byłyby większe od $2n$ przez co nie mogłyby być w zbiorze $S$, zatem $c$ jest mniejsze od $n$. Jeśli $c$ jest mniejsze od $n$ zatem istnieje taka para liczb $0 < d,e < n$ taka że $cd = a$ i $ce = b$ oraz $d \nmid e$. Skoro $d\nmid e$ zatem $cd \nmid ce \implies a \nmid b$.
:::

### zależność rekurencyjna
\begin{gather*}
Q_n = 1 + n + \frac{1}{n}\sum_{k=0}^{n-1}(Q_k + Q_{n-k-1}) \\
Q_n = 1 + n + \frac{2}{n}\sum_{k=0}^{n-1}Q_k \\
nQ_n = n+n^2+2\sum_{k=0}^{n-1}Q_k\\
nQ_n - 2\sum_{k=0}^{n-1}Q_k = n(n+1)\\
\sum_{k=0}^{n-1}(Q_n-2Q_k) = n(n+1)\\
nQ_n = n+n^2+2\sum_{k=0}^{n-1}Q_k\\
(n-1)Q_{n-1} = (n-1) + (n-1)^2 + 2\sum_{k=0}^{n-2}Q_k \\
nQ_n - (n-1)Q_{n-1} = 1 - 1 + 2n + 2Q_{n-1} \\
nQ_n - (n+1)Q_{n-1} = 2n\\
Q_n - \frac{n+1}{n}Q_{n-1} = 2\\
Q_n = 2 + \frac{n+1}{n}Q_{n-1} = 2 + \frac{n+1}{n}\left(2 + \frac{n}{n-1}Q_{n-2}\right)=\\
= 2 + \frac{n+1}{n}2 + \frac{n+1}{n}\frac{n}{n-1}Q_{n-2} = 2 + \frac{n+1}{n}2 + \frac{n+1}{n-1}Q_{n-2} =2+ 2(n+1)\sum_{k=0}^{n-1}\frac{1}{n-k}=\\
=2+ 2(n+1)\sum_{k=1}^{n}\frac{1}{k}= 2+2(n+1)H_n
\end{gather*}

### zliczanie permutacji
### kurczaki z maka
https://mikebeneschan.medium.com/the-chicken-mcnugget-theorem-explained-2daca6fbbe1e
Claim 1: ab-a-b is unpurchaseable.

We’re going to use a proof by contradiction. We start by assuming the opposite of the claim: assume that ab-a-b is purchasable. If ab-a-b is purchasable, that means there exist nonnegative numbers x and y such that ax+by=ab-a-b.

If we divide (ax+by) by a, we get a remainder of by. So (ax+by)≡by(mod a). Similarly, (ab-a-b)≡ -b(mod a). In turn, since ax+by=ab-a-b, this implies that by≡ -b(mod a).

Since b and a are relatively prime, b must have a multiplicative inverse mod a. Let’s call this inverse b’. If we multiply both sides of by≡ -b(mod a) by the inverse b’, this happens:

b’by≡ b’-b(mod a)

(b’b)y≡ -1(b’b)(mod a)

y≡ -1(mod a)

Similarly, if we divide both sides of the original equation (ax+by=ab-a-b) by b, we can reason that x≡-1 (mod b).

We know that x and y cannot be equal to -1, because we specified that they’re nonnegative (You can’t buy “-1 packs” of chicken nuggets). So the smallest possible value of x is b-1, and the smallest possible value of y is a-1. In other words, x≥b-1 and y≥a-1.

But if x≥b-1 and y≥a-1, it leads us to the following:

ab-a-b=ax+by ≥ a(b-1)+b(a-1)= ab-a+ab-b= 2ab-a-b > ab-a-b.

This would mean that ab-a-b > ab-a-b, which is clearly a contradiction. Since ab-a-b being purchasable leads to a contradiction, we know that ab-a-b must be unpurchasable.

Claim 2: Any n > ab-a-b is purchasable.

We now know that ab-a-b is unpurchaseable, but we also want to show that ab-a-b is the largest unpurchaseable number.

This proof is going to get more complicated than claim 1. To start, we have to invoke the name of a dead French guy. That’s right, it’s time for Bézout’s Identity:

Bézout’s Identity: If a and b are integers, then there exist integers x,y such that ax+by=gcd(a,b).

In this case, gcd(a,b)=1, so there exist some integers (x,y) such that ax+by=1. Multiplying both sides of the equation by n gives us nax+nby=n.

Let’s define x’=nx and y’=ny to make our formula a little cleaner: ax’+by’=n. Now I’m going to throw another claim at you:

Lemma: If (x’,y’) is a solution to ax’+by’=n, then (x’-kb, y’+ka) is also a solution for any integer k.

Proof: a(x’-kb)+b(y’+ka) = ax’-akb+by’+akb = ax’+by’=n.

Looking at the number x’-kb, k refers to the number of multiples of b that we add or subtract from x’. Note that we’re able to pick a specific value of k so that x’-kb is between 0 and b-1 (0≤ x’-kb ≤b-1). Let’s call this specific value k’, and we’ll define x”=x’-k’b and y”=y’+k’a. From the lemma, we know that (x”,y”) is a solution to ax+by=n. But we’re not quite done. We still have to prove that x” and y” are nonnegative.

x” is nonnegative by definition: we defined it as 0≤ x” ≤b-1. Now we need to show that y” is nonnegative. We know that n=ax”+by”, and n>ab-a-b. Putting those together, this happens:

ax”+by” > ab-a-b →

by”+b > ab-a-ax” →

b(y”+1) > a(b-1-x”)

We know that x”≤b-1, which means that b-1-x”≥0. The number a is positive, so this also means a(b-1-x”)≥0, which means b(y”+1)>0. Since b is positive, (y”+1)>0 and thus y”≥0. We’ve now shown that x” and y” are nonnegative, which means that the number n is purchasable. QED.

### jezo tetris

Zadanie 5
Ze względu na szerokość 1-go klocka mamy a_1 = a_2 = 1. Dla większych n możemy zauważyć, że zachodzi następująca zależność:

$a_n = a_{n-1} + 2*(a_{n-3} + a_{n-5} + .. + a_{n-1 mod 2})$,

analizując maksymalne j<n takie, że prefiks 1,..,j oraz sufiks j+1,..,n są niezależnie wykafelkowane zgodnie z regułami. Gdy w n-tej kolumnie są 2 pojedyncze kostki (2-gi klocek), to j=n-1. Gdy zaś w n-tej kolumnie znajduje się część klocka 1-go typu, który może być wtedy ułożony na 2-możliwe sposoby, to po lewej kończy się on w kolumnie n-2 --- gdy w kolumnie (n-2) jest oprócz niego pojedyncza kostka, to j=n-3, w przeciwnym razie drugi klocek 2-go typu z tej kolumny kończy się w kolumnie n-5 i mamy analogiczną sytuację jak poprzednio. Zauważmy ponadto, że dla poprawności tego wzoru powinniśmy przyjąć a_0=1.

Zapisując tę samą zależność co powyżej dla n-2 i odejmując od powyższej, otrzymujemy

$a_n - a_{n-2} = a_{n-1} + a_{n-3}$,

lub równoważnie

$a_n = a_{n-1} + a_{n-2} + a_{n-3}$,

co jest zależnością podobną jak ta dla liczb Fibonacciego. Zachodzi ona dla n >= 3. Korzystając z tej zależności, wyprowadzenie wzoru na funkcję tworzącą jest standardowym ćwiczeniem (znów: podobnie jak dla ciągu Fibonacciego).