[toc]
## Các khái niệm, tính chất
- Cây (tree) là một đồ thị vô hướng liên thông không có chu trình.
- Tập hợp các cây không có đỉnh chung gọi là một rừng (forest).

- Các khái niệm: bậc của nút, bậc của cây, nút cha, nút con, nút gốc, nhánh, lá, mức của nút, độ dài đường đi từ gốc đến nút x, tổng độ dài, độ dài trung bình, độ cao của cây...
## 1. Cây nhị phân (Binary tree)
- **Khái niệm:** Cây nhị phân là cây mà mỗi nút có tối đa 2 cây con.
- **Một số tính chất:**
+ Số nút nằm ở mức $i \le 2^i$.
+ Số nút lá $\le 2^{h-1}$, với $h$ là chiều cao của cây.
+ Chiều cao của cây $h \ge \log_2(N)$, với $N$ là số nút trong cây).
+ Số nút trong cây $\le 2^{h-1}$.
- **Các loại cây nhị phân:** cây nhị phân hoàn chỉnh, cây nhị phân đầy đủ (hoàn chỉnh + các nút lá có cùng mức), cây nhị phân cân bằng...


- **Biểu diễn cây nhị phân:**
```cpp=
struct Node{
int data;
Node* left;
Node* right;
};
```
- **Duyệt cây nhị phân:**
**- Theo chiều rộng:** Là cách thăm các nút bắt đầu từ bậc thấp (hoặc cao nhất) và di chuyển xuống dưới (hoặc lên trên) theo bậc. Ở mỗi bậc thăm nút từ trái sang phải (hoặc từ phải sang trái).
- Thứ tự theo hình trên: $1$ $2$ $3$ $4$ $5$ $6$ $7$.
```cpp=
void printLevelOrder(Node* root){
if (root == NULL) return;
queue <Node*> q;
while(q.size() > 0){
Node* tmp = q.front(); // lấy phần tử đầu tiên
q.pop(); // xóa khỏi hàng đợi
cout<<tmp->data<<" ";
// thêm các nút con
if (tmp->left != NULL)
q.push(tmp->left);
if (tmp->right != NULL)
q.push(tmp->right);
}
}
```
**- Theo chiều sâu:** có 3 cách cơ bản
a. Duyệt tiền thứ tự: gốc - trái - phải
- Thứ tự theo hình trên: $1$ $2$ $4$ $5$ $3$ $6$ $7$.
```cpp=
void NLR(Node* root){ // Node - Left - Right
if (root != NULL){
cout<<root->data<<" ";
NLR(root->left);
NLR(root->right);
}
}
```
b. Duyệt trung thứ tự: trái - gốc - phải
- Thứ tự theo hình trên: $4$ $2$ $5$ $1$ $6$ $3$ $7$.
```cpp=
void LNR(Node* root){ // Left - Node - Right
if (root != NULL){
LNR(root->left);
cout<<root->data<<" ";
LNR(root->right);
}
}
```
c. Duyệt hậu thứ tự: trái - phải - gốc
- Thứ tự theo hình trên: $4$ $5$ $2$ $6$ $7$ $3$ $1$
```cpp=
void LRN(Node* root){ // Left - Right - Node
if (root != NULL){
LRN(root->left);
LRN(root->right);
cout<<root->data<<" ";
}
}
```
## 2. Cây nhị phân tìm kiếm (Binary search tree - BST)
### Khái niệm:
- Là cây nhị phân trong đó tại mỗi nút, khóa của nút đang xét lớn hơn khóa của tất cả các nút thuộc cây con trái và nhỏ hơn khóa của tất cả các nút thuộc cây con phải. Ví dụ:

### Các thao tác:
#### Tìm kiếm một phần tử
```cpp=
Node* searchNode(Node* root, int key){
if (root == NULL) return root;
else if (root->data == key)
return root;
else if (root->data < key)
return searchNode(root->right, key);
else
return searchNode(root->left, key);
}
```
#### Thêm một phần tử
```cpp=
void insertNode(Node* root, int key){
Node* tmp = searchNode(root, key);
if (tmp == NULL){
tmp = new Node;
tmp->data = key;
tmp->left = tmp->right = NULL;
}
}
```
#### Xóa một phần tử
```cpp=
void replaceNode(Node* &p, Node* &t){
if(t->left != NULL){
replaceNode(p,t->right); // tìm nút trái nhất cây con phải
}
else{
p->data = t->data;
p = t;
t = t->right;
}
}
void deleteNode(Node* root, int key){ // xóa phần tử khóa key
Node* tmp = searchNode(root, key); // tìm nút có khóa là key
if (tmp == NULL) return root; // dừng nếu không tồn tại nút có khóa key
Node* p = tmp;
if (tmp->left == NULL){ // không có con trái, chỉ có thể có 1 con phải hoặc không
tmp = tmp->right;
}
else if (t->right == NULL){ // không có con phải, chỉ có thể có 1 con trái hoặc không
tmp = tmp->left;
}
else { // nút có đủ 2 con
replaceNode(p,tmp->right); // trường hợp tìm nút trái nhất của cây con phải
}
delete p; //p bây giờ lưu địa chỉ của nút thay thế - không còn cần sử dụng nữa
}
```
#### Hủy toàn bộ cây: duyệt LRN
### Nhận xét:
- Tất cả các thao tác đều có độ phức tạp trung bình là $O(h)$, với $h$ là chiều cao của cây.
- Trong trường hợp tốt nhất $h=\log_2(n)$.
- Trong trường hợp xấu nhất, cây bị suy biến (đường thẳng), khi đó $h=n$.
=> Vì vậy cần cải tiến cấu trúc của BST để đạt được chi phí có các thao tác là $\log_2(n)$.
## Cây AVL (Cây nhị phân cân bằng)
- Mô tả:
- Là cây tìm kiếm nhị phân (BST) tự cân bằng.
- Tại mọi nút, chiều cao của hai cây con chênh lệch không quá 1.
- Khi tính cân bằng AVL tại một nút bị phá vỡ, cần một hoặc hai phép quay để tái cân bằng AVL cây tại nút đó và biến đổi cây trở thành cân bằng AVL.
- Xây dựng cây AVL
```cpp=
struct Node{
int data;
Node* left;
Node* right;
int height;
}
```
- Chiều cao của một Node chính là số các node trên một đường dẫn dài nhất từ Node đó đến Node = NULL. Và quy ước Node = NULL có chiều cao bằng 0.
```cpp=
int getHeight(Node* root){// lấy chiều cao của một nút
if (root==NULL) return 0;
return root->height;
}
```
- Đối với một cây cân bằng, chỉ số cân bằng (CSCB) của mỗi nút chỉ có thể mang một trong ba giá trị sau đây:
$CSCB(p)=0$ ⇔ Độ cao cây trái $(p)$ = Độ cao cây phải $(p)$
$CSCB(p)=1$ ⇔ Độ cao cây trái $(p)$ > Độ cao cây phải $(p)$
$CSCB(p)=-1$ ⇔ Độ cao cây trái $(p)$ < Độ cao cây phải $(p)$
* Các kĩ thuật quay cây AVL
Có thể thấy cây BST khi không cân bằng sẽ bị lệch sang phía bên trái hoặc bên phải. Để điều chỉnh lại ta cần phải quay cây sang phía ngược lại.
- Quay trái: áp dụng khi cây bị lệch phải

- Quay phải: áp dụng khi cây bị lệch trái

```cpp=
Node* rightRotate(Node* root){
Node* x=root->left;
//Quay phai
root->left=x->right;
x->right=root;
//Cap nhat chieu cao
root->height=1+ max(getHeight(root->right), getHeight(root->left));
x->height=1+ max(getHeight(x->right), getHeight(x->left));
//Tra ve nut goc hien tai
return x;
}
Node* leftRotate(Node* root){
Node* y=root->right;
//Quay trai
root->right=y->left;
y->left=root;
//Cap nhat chieu cao
root->height=1+ max(getHeight(root->right), getHeight(root->left));
y->height=1+ max(getHeight(y->right), getHeight(y->left));
//Tra ve nut goc hien tai
return y;
}
```
### Các trường hợp cây bị lệch
a. Trái trái

- Xảy ra khi: $height(X)$ – $height(Y)$ > $1$ và $value(Đỏ)$ < $value(X)$
- Xử lý: quay phải Node root
`rotateRight(root)`
b. Phải phải

- Xảy ra khi: $height(X)$ – $height(Y)$ < $-1$ và value(Đỏ) > value(Y)
- Xử lý: quay trái Node $root$
`rotateLeft(root)`
c. Trái phải

- Xảy ra khi: $height(X)$ – $height(Y)$ < $1$ và $value(Đỏ)$ > $value(X)$
- Xử lý: `rotateLeft(X)` $\rightarrow$`rotateRight(root)`
d. Phải trái

- Xảy ra khi: $height(X)$ – $height(Y)$ < $-1$ và $value(Đỏ)$ < $value(Y)$
- Xử lý: `rotateRight(Y)` -> `rotateLeft(root)`
- Nhận xét:
+ Các thao tác có độ phức tạp $O(\log_2(n))$.
+ Với cây cân bằng trung bình 2 lần thêm vào cây thì cần một lần cân bằng lại; 5 lần hủy thì cần một lần cân bằng lại.
+ Nhưng khi ta thêm rất nhiều Node vào cây thì sẽ khiến cây phải quay (cân bằng) liên tục. Cây có càng nhiều phần tử thì việc cân bằng lại cây sẽ càng mất công hơn. Cây đỏ đen sẽ khắc phục yếu điểm này.
[Minh họa thuật toán ở đây](https://visualgo.net/en/bst)
## Cây đỏ đen (Red-black tree)
- Là cây tìm kiếm nhị phân (BST) tự cân bằng thỏa mãn các tính chất sau:
+ Một nút hoặc là đỏ hoặc là đen.
+ Gốc là đen.
+ Tất cả các lá (NULL) là đen.
+ Cả hai con của mọi nút đỏ là đen. (và suy ra mọi nút đỏ có nút cha là đen)
+ Tất cả các đường đi từ một nút bất kỳ tới các lá có số nút đen bằng nhau.
### Ví dụ
[Tại đây](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html)
### Các thao tác trên cây
#### Tìm kiếm
Giống với [tìm kiếm trong cây nhị phân tìm kiếm](#Tìm-kiếm-một-phần-tử)
#### Thêm phần tử
Gọi phần tử được thêm vào là $X$
- $X$ sẽ là nút đỏ.
- Nếu $X$ là gốc, chuyển $X$ thành màu đen.
- Nếu như cha của $X$ màu đỏ.
- Nếu như bác của $X$ (anh em với cha của $X$) màu đỏ, chuyển màu của cha và bác thành đen, chuyển màu ông của $X$ (cha của cha $X$) thành đỏ, tiếp tục với ông của $X$.
- Nếu như bác của $X$ màu đen, ta có 4 trường hợp xoay cây giống với cây AVL. Với trường hợp trái trái và phải phải, sau khi xoay cây thì ta sẽ tráo đổi màu của ông và cha của $X$. Trường hợp trái phải và phải trái thì ta sẽ tráo đổi màu của ông của $X$ với $X$.
## Cây phân trang
### Khái niệm
- Là cây M-phân tìm kiếm.
- $\displaystyle\left\lceil {\frac{M}{2}} \right\rceil \le$ số cây con mà mỗi node (trừ gốc và lá) có thể chứa $\le M$.
- $\displaystyle\left\lceil {\frac{M}{2}} \right\rceil - 1 \le$ số khoá mà mỗi node (trừ gốc) có thể có $\le M - 1$.
- $1 \le$ Số khoá mà node gốc có thể có $M - 1$.
- Trong mỗi node, các khoá được sắp xếp tăng dần.
- Các node lá nằm cùng mức.
- Các khoá trong node con $C_x$ sẽ lớn hơn khoá nàm trước nó và nhỏ hơn khoá nằm sau nó.
### Ví dụ

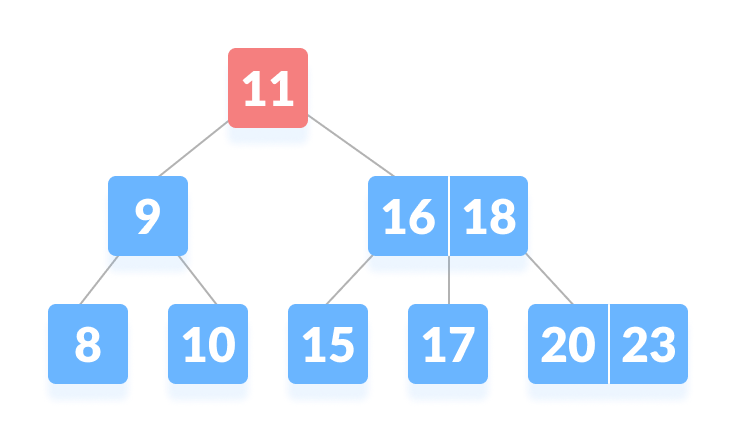
[Tại đây](https://www.cs.usfca.edu/~galles/visualization/BTree.html)
### Các thao tác
#### Tìm kiếm
- Bắt đầu với các khoá trên node gốc.
- Nếu $K_i < x < K_{i + 1}$, tìm kiếm bên trong cây con ở giữa $K_i$ và $K_{i + 1}$.
- Nếu $K_{M} < X$, tìm kiếm ở cây con bên phải cùng.
- Nếu $K_1 > X$, tìm kiếm ở cây con bên trái cùng.
- Nếu đã duyệt hết nhưng không tìm thấy, không tồn tại khoá và node giứa giá trị $X$.
#### Thêm khoá
- Thêm khoá mới vào các lá
- Nếu node chưa đầy khoá, thêm khoá vào node.
- Nếu node đã đầy, thực hiện tách node.
+ Khoá trung vị của node sẽ được đưa lên node cha.
+ 2 phần còn lại sẽ thành 2 cây con được nối lên node cha trong cùng mức.
#### Xoá khoá
- Nếu khoá nằm trên lá, xoá bình thường.
- Nếu vi phạm quy tắc hoặc node cần xoá không phải lá, ta sẽ tìm khoá thay thế. Thường là khoá trái nhất ở cây con bên phải và ngược lại.
 Sign in with Wallet
Sign in with Wallet

