# Introduction to Problem Solving
---
title: Introduction
description: Basic Introduction and FAQ
duration: 150
card_type: cue_card
---
Hey Everyone, welcome to your first session at Scaler!
I hope that you have a great time learning and interacting here.
I want to know about everyone here, so please send 2 lines about yourself in chat!
Alright, to begin with let me start with my Introduction.
> Note to Instructor: Introduce Yourself.
### Few Terms that you shall see/hear throughout the course:
> Note to Instructor: Please take a screenshot of below content and keep it pasted on your Ipad.
1. **PSP (Problem Solving Percentage) - Solved Assignment Problems / Total Open Assignment Problems**
* There are two types of section - Assignment and Additional. Assignment section consists of implementation of the problems done in class. PSP is calculated based on only Assignment Problems.
* Additional Problems are slight modifications of assignment problem, they are not part of PSP but once you're done with assignment, we highly recommend to complete additional problems as well.
* Try to keep PSP least 85% no matter what. It shall really help you to stay focused and we have seen in the past that people with >= 85%, do well in contests and mock Interviews
2. **Attendance**
* Try to maintain at-least 80% attendance either through live classes or by watching recording, though I will recommend you to come to classes regularly because otherwise it may create backlogs.
* So, I expect all of you to attend live classes and if for any reason you are unable to, then please send me a message stating the reason.
I shall be looking at your performances very closely and if I see a dip, I’ll be reaching out to you to understand the issues.
Though I would encourage you to reach out (either via slack/WA DM) if there’s anything troubling you so that we can sort it out together and let not that dip happen!
---
title: Intermediate Module Description
description: Intermediate Module Description
duration: 400
card_type: cue_card
---
> Note to Instructor: Please keep the below content pre-written on your IPad.
* Introduction to Problem Solving
* Time Complexity
* Introduction to Arrays
* Prefix Sum
* Carry Forward & Subarrays
* Sliding Window & Contribution Technique
* Memory Management
* Sorting Basics
* 2D Matrices
* Bit Manipulations Basics
* Strings
* Interview Problems
* Contest [covers Full Intermediate DSA]
**Note:**
1. In Intermediate, we shall be learning the concepts around different topics and how to work with certain data structures.
* This module is dedicated to make you comfortable with Programming.
2. Contest will be held after Intermediate Module.
* It'll will be for 1.5 hours and will be conducted within class duration followed by Contest Discussion (Instructor shall be discussing contest problems).
* If for any reason you are unable to clear the contest, then we shall also be having re-attempts. (**Passing criteria - total questions will be 4, out of which atleast 3 needs to be solved**)
* It is recommended to participate in live contest since discussion happens for it but for re-attempt, it doesn't happen.
* Hence, it is important to give live to be able to understand mistakes.
* Rely on re-attempts in worst scenarios. Though, best of any attempt shall be considered.
* People who regularly participate in contests are more likely to do better in real Interviews.
3. Be consistent in solving problems. If stuck, please post the issue in your WA/Slack group and let's make it a habit of helping each other as it will eventually help you to be better.
### FAQs :
- Notes will be uploaded after the class.
- Assignments will be unlocked after the class ends.
- There is no deadline for assignments.
Let's Begin with the Content!
---
title: Agenda for Today!
description: agenda
duration: 500
card_type: cue_card
---
> Note: In today's session we are not going to study any data structure. Rather we will see the power of making Observations.
> We'll learn how to approach any problem i.e, the sequence of steps to be followed to solve a problem.
Following will be covered today!
1. Count the Factors
2. Optimisation for counting the Factors
3. Check if a number is Prime
4. Sum of N Natural Numbers
6. How to find the number of a times a piece of code runs, i.e, number of Iterations.
7. How to compare two Algorithms.
---
title: Count of factors of a number N
description: Count of factors of a number N
duration: 500
card_type: cue_card
---
Q. What is a factor?
A. We say i is a factor of N if i divides N completely, i.e the remainder is 0.
How to programmatically check if i is a factor of N ?
We can use % operator which gives us the remainder.
=> **N % i == 0**
### Question:
Given N, we have to count the factors of N.
**Note:** N > 0
---
title: Quiz 1
description: Quiz 1
duration: 45
card_type: quiz_card
---
# Question
Number of factors of the number 24.
# Choices
- [ ] 4
- [ ] 6
- [x] 8
- [ ] 10
---
title: Quiz 1 Explanation
description:
duration: 45
card_type: cue_card
---
**Explanation:**
1, 2, 3, 4, 6, 8, 12, and 24 are the factors.
---
title: Quiz 2
description: Quiz 2
duration: 45
card_type: quiz_card
---
# Question
Number of factors of the number 10.
# Choices
- [ ] 1
- [ ] 2
- [ ] 3
- [x] 4
---
title: Quiz 2 Explanation
description:
duration: 45
card_type: cue_card
---
**Explanation:**
1, 2, 5, and 10 are the factors.
---
title: Counting Factors Brute force solution
description:
duration: 500
card_type: cue_card
---
What is the minimum factor of a number ?
=> 1
What is the maximum factor of a number ?
=> The number itself
So, we can find all factors of N from 1 to N.
### Pseudocode
```cpp=
function countfactors (N){
fac_count = 0
for(i -> 1 to N) {
if (N % i == 0)
fac = fac + 1
}
return fac
}
```
## NOTE: Now that you all are well aware of language basics of your language, like writing basic for loop, while, loop, if else, array declaration, etc.. the codes will be writing as pseudocodes. What are they? => please explain by writing below code.
### Observations for Optimised Solution
* Now, your code runs on servers.
* When you submit your code, do you expect some time within which it should return the Output ?
* You wouldn't want to wait when you even don't know how long to wait for ?
* Just like that one friend who says, 'Just a little more time, almost there.' And you feel annoyed, not knowing how much longer you'll have to wait.
Servers have the capability of running ~10^8 Iterations in 1 sec.
Please note that this is a standard assumption accross all platforms.
> Note: We shall be learning more about it in next session
Explain the time taken by above code for below values of N and need for Optimisation.
|N| Iterations| Execution Time|
|-|----------|---------- |
|10^8| 10^8 iterations| 1 sec |
|10^9| 10^9 iterations| 10 sec |
|10^18| 10^18 iterations| 317 years |
So, for N = 10^18, to just get the number of factors, we need around 317 years.
*Would you be alive to watch the O/P ?
Your children ?
3rd Gen ?
4th Gen ?
............. too long to wait.*
---
title: Optimisation for Counting Factors
description: Optimized solution
duration: 1500
card_type: cue_card
---
**Optimization:**
i * j = N -> {i and j are factors of N}
=> j = N / i -> {i and N / i are factors of N}
For example, N = 24
|i| N / i|
|-|----------|
|1| 24|
|2| 12|
|3| 8|
|4| 6|
|6| 4|
|8| 3|
|12| 2|
|24| 1|
Q. Can we relate these values?
A. We are repeating numbers after a particular point. Here, that point is from 5th row.
Now, repeat the above process again for N = 100.
|i| N / i|
|-|----------|
|1| 100|
|2| 50|
|4| 25|
|5| 20|
|10| 10|
|20| 5|
|25| 4|
|50| 2|
|100| 1|
The factors are repeating from 6th row. After a certain point factors start repeating, so we need to find a point till we have to iterate.
We need to only iterate till -
**`i <= N/i`**
**`i * i <= N`**
### Pseudocode
```cpp=
function countfactors(N){
fac_count = 0
for(i -> 1 till i*i <= N) {
if (N % i == 0)
fac = fac + 2
}
return fac
}
```
Q. Will the above work in all the cases?
A. No, not for perfect squares. Explain this for N = 100, what mistake we are doing. We will count 10 twice.
**Observation:** Using the above example, we need to modify the code for perfect squares.
### Pseudocode with Edge Case Covered
```cpp=
function countfactors(N){
fac_count = 0
for(i -> 1 till i*i <= N) {
if (N % i == 0){
if(i == N / i){
fac = fac + 1
}
else {
fac = fac + 2
}
}
}
return fac
}
```
Dry run the above code for below examples,
N = 24, 100, 1.
### What's the number of iterations now ?
We are running loop till i * i <= N
Let's evaluate it -
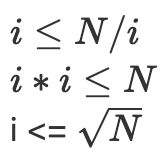
|N| Iterations| Execution Time|
|-|----------|---------- |
|10^18| 10^9 iterations| 10 secs |
**Conclusion:** Most important skill for problem solving is observation.
>How beautifully we have been able to reduce the Iterations just by making some Observations!
### Follow Up Question
Given N, You need to check if it is prime or not.
---
title: Quiz 3
description: Quiz 3
duration: 45
card_type: quiz_card
---
# Question
How many prime numbers are there?
10, 11, 23, 2, 25, 27, 31
# Choices
- [ ] 1
- [ ] 2
- [ ] 3
- [x] 4
---
title: Quiz 3 Explanation
description:
duration: 45
card_type: cue_card
---
**Explanation:**
Q. What is a prime Number?
A. Number which has only 2 factors, 1 and N itself.
So, 11, 23, 2, and 31 are the only prime numbers since they all have exactly 2 factors.
---
title: Prime Check
description: Prime Check
duration: 150
card_type: cue_card
---
Our original question was to check if a number is prime or not. For that, we can just count the number of factors to be 2.
```cpp=
function checkPrime(N){
if countfactors(N) == 2
return true
else
return false
}
```
For N = 1, it will return false, which is correct. Since, 1 is neither prime nor composite.
---
title: Some Basic Math Properties
description:
duration: 45
card_type: cue_card
---
**Some basic math properties:**
1. `[a,b]` - This type of range means that a and b are both inclusive.
2. `(a,b)` - This type of range means that a and b are both excluded.
---
title: Quiz 4
description: Quiz 4
duration: 30
card_type: quiz_card
---
# Question
How many numbers are there in the range [3,10]?
# Choices
- [ ] 7
- [ ] 6
- [x] 8
- [ ] 10
---
title: Quiz 4 Explanation
description:
duration: 60
card_type: cue_card
---
**Explanation:**
The range [3,10] includes all numbers from 3 to 10, inclusive. Inclusive means that both the lower bound (3) and the upper bound (10) are included in the range. Thus the numbers that are included are 3 4 5 6 7 8 9 10.
---
title: Quiz 5
description: Quiz 5
duration: 45
card_type: quiz_card
---
# Question
How many numbers are there in the range [a,b]?
# Choices
- [ ] b - a
- [x] b - a + 1
- [ ] b - a - 1
- [ ] Ahhh.. too tricky to calculate
---
title: Quiz 5 Explanation
description:
duration: 30
card_type: cue_card
---
**Explanation:**
To find the number of numbers in a given range, we can subtract the lower bound from the upper bound and then add 1. Mathematically, this can be expressed as:
```
Number of numbers in the range
= Upper bound - Lower bound + 1
```
---
title: Quiz 6
description: Quiz 6
duration: 60
card_type: quiz_card
---
# Question
1 + 2 + 3 + 4 + 5 + 6 + ... + 100 = ?
# Choices
- [ ] 1010
- [x] 5050
- [ ] 5100
- [ ] 1009
---
title: Quiz 6 Explanation
description:
duration: 200
card_type: cue_card
---
**Explanation:**

Generalize this for the first N natural numbers.

---
title: What do we mean by Iteration?
description: Meaning of Iteration
duration: 60
card_type: cue_card
---
The number of times a loop runs, is known as Iteration.
---
title: Quiz 7
description: Quiz 7
duration: 45
card_type: quiz_card
---
# Question
How many times will the below loop run ?
```
for(i -> 1 to N)
{
if(i == N) break;
}
```
# Choices
- [ ] N - 1
- [x] N
- [ ] N + 1
- [ ] log(N)
---
title: Quiz 8
description: Quiz 8
duration: 45
card_type: quiz_card
---
# Question
How many iterations will be there in this loop ?
```
for(i -> 0 to 100){
s = s + i + i^2;
}
```
# Choices
- [ ] 100 - 1
- [ ] 100
- [x] 101
- [ ] 0
---
title: Quiz 9
description: Quiz 9
duration: 45
card_type: quiz_card
---
# Question
How many iterations will be there in this loop?
```
func(){
for(i -> 1 to N){
if(i % 2 == 0){
print(i);
}
}
for(j -> 1 to M){
if(j % 2 == 0){
print(j);
}
}
}
```
# Choices
- [ ] N
- [ ] M
- [ ] N * M
- [x] N + M
---
title: Quiz 9 Explanation
description:
duration: 60
card_type: cue_card
---
**Explanation:**
We are executing loops one after the other. Let's say we buy first 5 apples and then we buy 7 apples, the total apples will be 12, so correct ans is N + M
---
title: Geometric Progression
description:
duration: 150
card_type: cue_card
---
## Geometric Progression (G.P.)
> **Example for intution:**
```
5 10 20 40 80 ..
```
In these type of series, the common ratio is same. In the given example the common ratio r is
= 10/5
= 20/10
= 40/20
= 80/40
= 2
**Generic Notation:**
a, a * r, a * r^2^, a * r^3^ ........a * r^n-1^
---
title: Sum of first N terms of a GP
description:
duration: 60
card_type: cue_card
---
**Sum of first N terms of GP:**
=
r cannot be equal to 1 because the denominator cannot be zero.
**Note:**
When r is equal to 1, the sum is given by a * n.
---
title: Real Life Examples of GP
description:
duration: 660
card_type: cue_card
---
## **Spreading of news**
Suppose one person spreads a news to 4 different people. Each one of those, spreads to 4 others, and so on..
<img src="https://d2beiqkhq929f0.cloudfront.net/public_assets/assets/000/086/636/original/Screenshot_2024-08-19_at_2.51.07_PM.png?1724059285" width=500 />
This can be denoted in form of GP which looks as follows-
1, 4, 16, 64, .....
### Number of people at 8th level
Now, if we want to figure out that at 8th level, how many people will know about this news, we can use formula for getting 8th term.
Formula for nth term = a * r^n-1^
a = 1, r = 4, n = 8
8th term = 1 * (4)^8-1^ = 16384
### Sum till 8th level
GP = 1, 4, 16, 64, 256, 1024, 4096, 16384
sum = a * ( r^#terms^ - 1)/ (r - 1)
= 1 * (4^8^ - 1)/(4 - 1)
= (65536-1)/3 = 65535/3 = 21845
#### **`Likewise, there can be multiple examples related to calculation of simple interest, spreading of a disease, growing population, depreciating value of car, etc...`**
---
title: How to compare two algorithms?
description: Comparing two algorithms using execution time
duration: 660
card_type: cue_card
---
## Story
There was a contest going on to SORT the array and 2 people took part in it (say Gaurav and Shila).
They had to sort the array in ascending order.
arr[5] = {3, 2, 6, 8, 1} -> {1, 2, 3, 6, 8}
Both of them submitted their algorithms and they are being run on the same input.
See this image to understand one important aspect of comparing two algorithms.
## Discussion
Can we use execution time to compare two algorithms?
Say initially **Algo1** took **15 sec** and **Algo2** took **10sec**.
This implies that **Shila's Algo 1** performed better, but then Gaurav pointed out that he was using **Windows XP** whereas Shila was using **MAC**, hence both were given the same laptops.........

## Conclusion
We can't evaluate algorithm's performance using **execution time** as it depends on a lot of factors like operating system, place of execution, language, etc.
### Question
How can we compare two algorithms?
Which measure doesn't depend on any factor?
**Answer:** Number of Iterations
**Why?**
* The number of iterations of an algorithm remains the same irrespective of Operating System, place of execution, language, etc.
---
title: Next Class Content
description: Topics that'll be taken up in next class
duration: 400
card_type: cue_card
---
Hold onto your seats because the next class is going to be an absolute thrill!
* We'll start the session by learning steps for calculating Big O, reasoning behind them and the drawbacks of it.
* We'll explore one concept of maths - **Logarithm**. Don't worry; we'll focus solely on what's relevant to the class, so you won't need to stress about anything outside of it.
* We'll end the session by learning Time Limit Exceeded Error and Importance of Constraints.
> NOTE TO INSTRUCTORS: Ask them to be done with today's assignment and let you know in the WA Group.
Ask them that they have to build this habit.
See you all in the next session!
 Sign in with Wallet
Sign in with Wallet

