[LTTĐCB - Chủ đề 4] Thiết kế giải thuật 4.2: Nhánh và Cận (Branch and Bound)

# I. Tổng quan ## 1. Giới thiệu phương pháp Trong lập trình cũng như trong thực tế, chắc hẳn các bạn đều đã gặp những bài toán với yêu cầu tìm kết quả ***tốt nhất*** thỏa mãn một hoặc một số điều kiện nào đó. Sự thật là chúng ta gặp các bài toán này khá thường xuyên, thậm chí vô cùng thực tiễn, chẳng hạn như: - Tìm cách trả số tiền $T$ với $n$ tờ tiền có mệnh giá cho trước, sao cho số tờ tiền cần sử dụng là nhỏ nhất? - Trong các nhà máy sản xuất vỏ lon đồ uống, các nhà thiết kế luôn luôn tìm cách thiết kế sao cho diện tích toàn phần của vỏ lon là nhỏ nhất nhằm giảm thiểu chi phí nguyên liệu. Bài toán đặt ra là với thể tích cần thiết là $V,$ làm sao để tạo ra vỏ lon hình trụ có diện tích toàn phần nhỏ nhất? $...$ Có rất nhiều bài toán như vậy trong Tin học, và chúng được gọi là các ***bài toán tối ưu***. Thông thường, người ta sẽ hay nghĩ đến phương pháp ***Quy hoạch động*** khi giải các bài toán tối ưu, tuy nhiên, phương pháp này chỉ có thể áp dụng nếu như bài toán đang xét có bản chất đệ quy mà thôi. Thực tế có nhiều bài toán tối ưu không có thuật toán nào thực sự hữu hiệu để giải quyết, mà vẫn phải sử dụng mô hình xem xét tất cả các phương án rồi đánh giá chúng để chọn ra phương án tốt nhất. Phương pháp ***Nhánh và Cận (Branch and Bound)*** chính là một phương pháp cải tiến từ phương pháp ***Quay lui***, được sử dụng để tìm nghiệm của bài toán tối ưu. ## 2. Ý tưởng Bước đầu tiên của phương pháp vẫn giống với ý tưởng của quay lui: Tìm cách biểu diễn nghiệm của bài toán dưới dạng một vector $(x_1, x_2,\dots, x_n),$ mỗi thành phần $x_i$ được chọn ra từ tập các ứng cử viên $S_i$. Bước tiếp theo sẽ hơi khác một chút: Nếu như ở phương pháp Quay lui, chỉ cần tuần tự chọn các ứng cử viên cho từng thành phần của vector nghiệm, thì ở phương pháp Nhánh và cận, mỗi nghiệm $X = (x_1, x_2, \dots, x_n)$ của bài toán sẽ được đánh giá ***độ tốt*** bằng một hàm $f(X)$. Vì đây là bài toán tối ưu, nên mục tiêu của chúng ta là đi tìm nghiệm có hàm $f(X)$ tốt nhất, thường là ***lớn nhất*** hoặc ***nhỏ nhất***. Bước thứ $3$ là xây dựng nghiệm của bài toán. Giả sử, các bạn đã xây dựng được $i$ thành phần của nghiệm là $(x_1, x_2,\dots, x_i)$ và chuẩn bị mở rộng nghiệm thành $(x_1, x_2,\dots, x_i, x_{i + 1})$. Nếu như bằng một cách nào đó, các bạn đánh giá được độ tốt của toàn bộ các nghiệm mở rộng của nhánh này là $(x_1, x_2,\dots, x_{i}, x_{i + 1},\dots)$ và biết rằng không có nghiệm nào trong nhánh này "tốt hơn" nghiệm tốt nhất tại thời điểm đó, thì việc mở rộng tiếp từ $(x_1, x_2,\dots, x_i)$ sẽ là không cần thiết nữa, mà thay vào đó ta sẽ chuyển qua chọn ứng cử viên tiếp theo cho thành phần $x_i$ luôn. Bằng phương pháp trên, ta sẽ loại bỏ được những nhánh không cần thiết để không duyệt vào các phương án đó, từ đó việc tìm ra nghiệm tối ưu sẽ nhanh hơn. Tuy nhiên, việc đánh giá được "độ tốt" của các nghiệm mở rộng không phải việc đơn giản, nhưng nếu làm được như vậy thì giải thuật sẽ thực thi nhanh hơn nhiều so với quay lui. ## 3. Lược đồ giải thuật Để thực hiện giải thuật Nhánh và Cận, các bạn có thể sử dụng một hàm đệ quy giống như giải thuật Quay lui, nhưng thêm phần đánh giá nghiệm trước khi xây dựng thành phần thứ $i$. Ngoài ra, ta cần sử dụng thêm một biến $\text{best\_solution}$ để ghi nhận nghiệm tốt nhất hiện tại. Dưới đây là mô hình cài đặt bằng C++: ```cpp= void branch_and_bound(i) { // Đánh giá các nghiệm mở rộng if ({Các_nghiệm_mở_rộng_đều_không_tốt_hơn_best_solution}) return; for (value in S[i]) { x[i] = value; // Ghi nhận thành phần thứ i. if ({Tìm_thấy_nghiệm}) best_solution = X; // Cập nhật lại best_solution bằng nghiệm vừa tìm được. else branch_and_bound(i + 1); // Chưa tìm thấy nghiệm thì xây dựng tiếp. {Loại_bỏ_thành_phần_thứ_i} } } ``` Bây giờ, hãy cùng đến với một số bài toán minh họa để hiểu rõ hơn về phương pháp! # II. Một số bài toán minh họa ## 1. Rút tiền ATM ### Đề bài Một máy ATM hiện có $n$ tờ tiền có giá trị lần lượt là $t_1, t_2,\dots, t_n$. Hãy tìm ra cách trả số tiền $S$ sao cho số tờ tiền phải sử dụng là ***ít nhất***? ***Input:*** - Dòng đầu tiên chứa hai số nguyên dương $n$ và $S$. - Dòng thứ hai chứa $n$ số nguyên dương $t_1, t_2,\dots, t_n$ phân tách nhau bởi dấu cách. ***Ràng buộc:*** - $1 \le n \le 20$. - $1 \le S \le 1000$. - $1 \le t_i \le 1000; \forall i: 1 \le i \le n$. ***Output:*** - Nếu như có thể trả số tiền $S$ thì in ra số tờ tiền ít nhất cần sử dụng và các tờ tiền được chọn, ngược lại in ra $-1$. ***Sample Input:*** ``` 10 390 200 10 20 20 50 50 50 50 100 100 ``` ***Sample Output:*** ``` 5 20 20 50 100 200 ``` ### Phân tích ý tưởng Nghiệm của bài toán có thể biểu diễn dưới dạng một vector gồm toàn các bit nhị phân $0 - 1$ là $x_1, x_2,\dots, x_n$ với ý nghĩa: $x_i = 0$ là tờ tiền thứ $i$ không được chọn, $x_i = 1$ là tờ tiền thứ $i$ được chọn. Mục tiêu chúng ta đang cần tìm một bộ nghiệm sao cho: $$\begin{cases}t_1 \times x_1 + t_2 \times x_2 + \cdots + t_n \times x_n = S.\\ (x_1 + x_2 + \cdots + x_n) \text{ MIN}. \end{cases}$$ Giả sử các bạn đã xây dựng được $i$ thành phần của nghiệm là $(x_1, x_2, \dots, x_i),$ tổng số tờ tiền đã sử dụng là $cnt$ và số tiền đã trả được là $sum,$ thì ta nhận xét thấy: - Số tiền còn lại cần trả là $S - sum$. - Nếu gọi $t_{max}[i + 1]$ là giá trị của tờ tiền lớn nhất trong các tờ tiền còn lại $(t_{max}[i + 1] = \text{max}\big(t_{i + 1}, t_{i + 2}, \dots, t_n)\big),$ thì ít nhất ta cần sử dụng thêm $\frac{S - sum}{t_{max}[i + 1]}$ tờ tiền nữa, tức là tổng số tờ tiền tối thiểu cần dùng của nhánh phương án này là $cnt + \frac{S - sum}{t_{max}[i + 1]}$. Gọi số tờ tiền của cách trả tốt nhất hiện tại là $\text{cnt\_best},$ thì nếu như $cnt + \frac{S - sum}{t_{max}[i]} \ge \text{best\_cnt},$ ta sẽ không cần phải mở rộng các nghiệm từ $(x_1, x_2,\dots, x_i)$ nữa. Để kiểm soát các tờ tiền được chọn, mình sử dụng thêm hai mảng là $\text{mark}$ để đánh dấu các tờ tiền được chọn trong một phương án, và $\text{mark\_best}$ để đánh dấu các tờ tiền được chọn trong phương án tốt nhất. ### Cài đặt ```cpp= #include <bits/stdc++.h> using namespace std; const int maxn = 21; int n, S, cnt, cnt_best, sum, a[maxn], mark[maxn], mark_best[maxn], maxmoney[maxn]; void enter() { ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); cin >> n >> S; for (int i = 1; i <= n; ++i) cin >> t[i]; } void create_data() { // cnt_best là số tờ tiền sử dụng trong phương án tốt nhất. // Ban đầu chưa có phương án nào, gán cnt_best = n + 1. best_cnt = n + 1; // t_max[i] lưu giá trị của tờ tiền lớn nhất từ i tới n. t_max[n] = t[n]; for (int i = n - 1; i >= 0; --i) t_max[i] = max(t_max[i + 1], t[i]); } // Nếu tìm được một phương án tốt hơn thì cập nhật lại kết quả. void update_best_solution() { if (sum == S && cnt < cnt_best) { cnt_best = cnt; for (int i = 1; i <= n; ++i) mark_best[i] = mark[i]; } } // In kết quả. void printf_result() { // Không tìm được cách trả tiền, in ra -1. if (cnt_best == n + 1) cout << -1; else // Tìm được thì in ra cách trả đó. { cout << cnt_best << endl; for (int i = 1; i <= n; ++i) if (mark_best[i]) cout << t[i] << ' '; } } void branch_and_bound(int i) { // Nếu nghiệm mở rộng của nhánh này không tốt hơn thì return. if (cnt + (S - sum) / t_max[i + 1] >= cnt_best) return; for (int j = 0; j <= 1; ++j) { // Ghi nhận thành phần thứ i. sum = sum + a[i] * j; mark[i] = j; cnt += j; if (i == n) update_best_solution(); else if (sum <= S) branch_and_bound(i + 1); // Loại bỏ thành phần thứ i. sum -= t[i] * j; cnt -= j; } } int main() { enter(); create_data(); branch_and_bound(1); printf_result(); return 0; } ``` ## 2. Bài toán Người du lịch ### Đề bài Có $n$ thành phố đánh số từ $1$ tới $n$. Giữa các cặp thành phố có thể có hoặc không có đường nối hai chiều, mạng lưới đường này được mô tả bằng một ma trận $C_{u, v},$ với ý nghĩa $C_{u, v} = C_{v, u}$ là chi phí để di chuyển giữa hai thành phố $u$ và $v$. Một người du lịch xuất phát từ thành phố $1,$ người này muốn đi thăm tất cả các thành phố khác, mỗi thành phố đúng một lần rồi quay trở lại thành phố $1$. ***Yêu cầu:*** Hãy tìm một hành trình cho người đó sao cho chi phí di chuyển là ít nhất? ***Input:*** - Dòng đầu tiên chứa số nguyên dương $n$. - $n$ dòng tiếp theo, mỗi dòng chứa $n$ số nguyên dương không vượt quá $100$ biểu thị ma trận $C$. ***Ràng buộc:*** - $1 \le n \le 20$. ***Output:*** - Dòng đầu tiên ghi chi phí nhỏ nhất. - Dòng thứ hai ghi một hành trình tìm được. 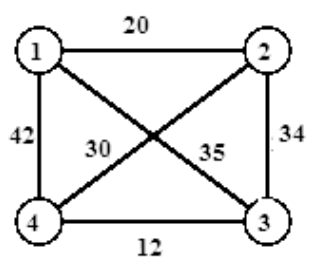***Sample Input:*** ``` 4 0 20 35 42 20 0 34 30 35 34 0 12 42 30 12 0 ``` ***Sample Output:*** ``` 97 1 2 4 3 1 ``` ***Hình minh họa:*** <center> ![](https://cdn.ucode.vn/uploads/2247/images/wcCrZpVO.png) </center> ### Phân tích ý tưởng Vector nghiệm của bài toán là một dãy $(x_1 = 1, x_2, x_3,\dots, x_n, x_{n + 1} = 1);$ với điều kiện giữa hai thành phố $x_i$ và $x_{i + 1}$ phải có đường đi trực tiếp. Ngoài ra, chỉ có thành phố $1$ được phép lặp lại $2$ lần. Vì thế, có thể thấy dãy $(x_1, x_2,\dots, x_n)$ là một hoán vị của $(1, 2, \dots, n)$. Ý tưởng duyệt quay lui như sau: Khi đã xây dựng được $(x_1, x_2,..., x_i),$ thì $x_{i + 1}$ có thể chọn một trong các thành phố mà có đường nối trực tiếp với nó, đồng thời chưa được chọn. Tuy nhiên, ta có thể áp dụng Nhánh và Cận để giảm độ phức tạp như sau: - Gọi chi phí tốt nhất hiện tại là $\text{best\_cost}$. - Với mỗi bước thử chọn $x_i,$ kiểm tra xem chi phí đường đi tính tới lúc đó có lớn hơn hoặc bằng chi phí tốt nhất hiện tại hay không. Nếu đã lớn hơn thì chọn ngay giá trị khác cho $x_i,$ bởi vì có đi tiếp theo nhánh này cũng sẽ chỉ tạo ra chi phí lớn hơn mà thôi. - Tới khi chọn được một giá trị $x_n$ thì cần kiểm tra xem chi phí tới $x_n$ cộng thêm chi phí từ $x_n$ về $1$ có tốt hơn chi phí tốt nhất hiện tại không? Nếu có thì cập nhật lại cách đi tốt nhất. ### Cài đặt Trong cài đặt dưới đây, giả thiết rằng giữa mọi cặp thành phố đều tồn tại đường đi, và chi phí $c_{u, v}$ luôn bằng $0$ nếu như $u = v$. Mảng $\text{visited}$ dùng để đánh dấu một thành phố đã được thăm hay chưa trong một cấu hình $X$. Mảng $x$ sử dụng để lưu cấu hình hiện tại, còn mảng $\text{x\_best}$ sử dụng để lưu cấu hình tốt nhất với $\text{best\_cost}$ là chi phí tốt nhất tìm được. ```cpp= #include <bits/stdc++.h> #define int long long #define task "tsp." #define inf 1e9 + 7 using namespace std; const int maxn = 21; int n, current_cost, best_cost; int visited[maxn], x_best[maxn], x[maxn], c[maxn][maxn]; void enter() { cin >> n; for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) cin >> c[i][j]; // Khởi tạo trước thành phố đầu tiên là 1, đồng thời đánh dấu nó đã thăm. x[1] = 1; visited[1] = 1; // Khởi tạo chi phí tối ưu bằng +oo, giả sử phương án hiện tại đang rất tệ. best_cost = inf; } // Cập nhật kết quả tốt nhất. void update_best_solution(int current_cost) { if (current_cost + c[x[n]][1] < best_cost) { best_cost = current_cost + c[x[n]][1]; for (int i = 1; i <= n; ++i) x_best[i] = x[i]; } } // In ra phương án tốt nhất tìm được. void print_best_solution() { cout << best_cost << endl; for (int i = 1; i <= n; ++i) cout << x_best[i] << "->"; cout << 1; } // Giải thuật nhánh và cận. void branch_and_bound(int i) { if (current_cost >= best_cost) return; for (int j = 2; j <= n; ++j) if (!visited[j]) { visited[j] = 1; x[i] = j; current_cost += c[x[i - 1]][j]; // Đã sinh xong một cấu hình, cập nhật chi phí tốt nhất. if (i == n) update_best_solution(current_cost); // Chưa sinh xong, tiếp tục sinh thành phần tiếp theo với chi phí tăng thêm. else branch_and_bound(i + 1); visited[j] = 0; current_cost -= c[x[i - 1]][j]; } } main() { ios_base::sync_with_stdio(false); cin.tie(nullptr); enter(); branch_and_bound(2); print_best_solution(); return 0; } ``` # III. Tài liệu tham khảo - https://www.geeksforgeeks.org/0-1-knapsack-using-branch-and-bound/ - https://www.geeksforgeeks.org/branch-and-bound-algorithm/ - <a href="https://cuongquach.com/ebook-giai-thuat-va-lap-trinh-lmh-pdf.html">Sách Giải thuật và Lập trình - thầy Lê Minh Hoàng</a>. - <a href="https://downloadsachmienphi.com/tai-lieu-giao-khoa-chuyen-tin-quyen-1/">Tài liệu giáo khoa chuyên Tin quyển 1 - thầy Hồ Sĩ Đàm</a>.

Syntax	Example	Reference
# Header	Header	基本排版
- Unordered List	Unordered List
1. Ordered List	Ordered List
- [ ] Todo List	Todo List
> Blockquote	Blockquote
Bold font	Bold font
Italics font	Italics font
~~Strikethrough~~	~~Strikethrough~~
19^th^	19^th
H~2~O	H₂O
++Inserted text++	Inserted text
==Marked text==	Marked text
[link text](https:// "title")	Link
![image alt](https:// "title")	Image
`Code`	`Code`	在筆記中貼入程式碼
```javascript var i = 0; ```	`var i = 0;`
:smile:		Emoji list
{%youtube youtube_id %}	Externals
$L^aT_eX$	L^aT_eX
:::info This is a alert area. :::	This is a alert area.