---
tags: vaje, rg, uvod
hackmd: https://hackmd.io/QCb4CmZTRH-gRMpKbnZ3Vg
plugins: mathjax
---
# Computational geometry - Tutorial 3.3.2021

---

## Introduction

### Exercise 1

Let $T(1) = O(1)$. Prove:

1. If $T(n) = O(n) + 2T(n/2)$, then $T(n) = O(n \log n)$.
2. If $T(n) = O(n) + T(n/2)$, then $T(n) = O(n)$.

----

Master theorem:

$$
T(n) = a T(n/b) + O(n^c) = \begin{cases}
O(n^c) & a < b^c \\
O(n^c \log n) & a = b^c \\
O(n^{\log_b a}) & a > b^c
\end{cases}
$$

1. $$
\begin{aligned}
T(n) &= O(n) + 2T(n/2) \\
&= O(n) + 2(O(n/2) + 2T(n/4)) \\
&= O(n + 2n/2 + 4n/4 + 8n/8 + \dots + n \cdot 1) \\
&= O(n \log n)
\end{aligned}
$$

2. $$
\begin{aligned}
T(n) &= O(n) + T(n/2) \\
&= O(n + n/2 + n/4 + \dots + 1) \\
&= O(n)
\end{aligned}
$$

---

### Exercise 2

Describe an algorithm which, given a list of points ${p_1}, {p_2}, \dots, {p_n}$ in $\mathbb{R}^2$, deletes the repeated points, i.e., returns the set $\lbrace {p_1}, {p_2}, \dots, {p_n} \rbrace$. The time complexity should be $O(n \log n)$.

Describe the algorithm for the same problem in $\mathbb{R}^d$. What is its time complexity?

----

* Sort points lexicographically $O(d n \log n)$
* Go through the sorted list and discard repeated points (check against the last seen point) $O(d n)$
* The algorithm works in $O(d n \log n)$ time

---

### Exercise 3

We are given $n$ segments in a plane. We know that the segments are the edges of a polygon, but they are not necessarily given in the "right" order. Describe an algorithm which reconstructs the polygon as a list of consecutive vertices in $O(n \log n)$ time.

----

* Construct a hash table mapping points to the two edges ending in that point $O(n)$
* Pick a point and follow the edges until we arrive at the starting point $O(n)$
* The algorithm works in $O(n)$ time


---

### Exercise 4

For the points $p = ({p_x}, {p_y})$, $q = ({q_x}, {q_y})$ and $r = ({r_x}, {r_y})$ in a plane, we define

$$
D(p, q, r) = \begin{vmatrix}
1 & p_x & p_y \\
1 & q_x & q_y \\
1 & r_x & r_y
\end{vmatrix} .
$$

1. Prove that $D(p, q, r) > 0$ holds if and only if the sequence $p, q, r$ is a left turn.
2. Prove that $D(p, q, r) = 0$ holds if and only if the points $p, q, r$ are collinear.
3. Prove that $\vert D(p, q, r) \vert$ equals twice the area of the triangle $\triangle pqr$.

----


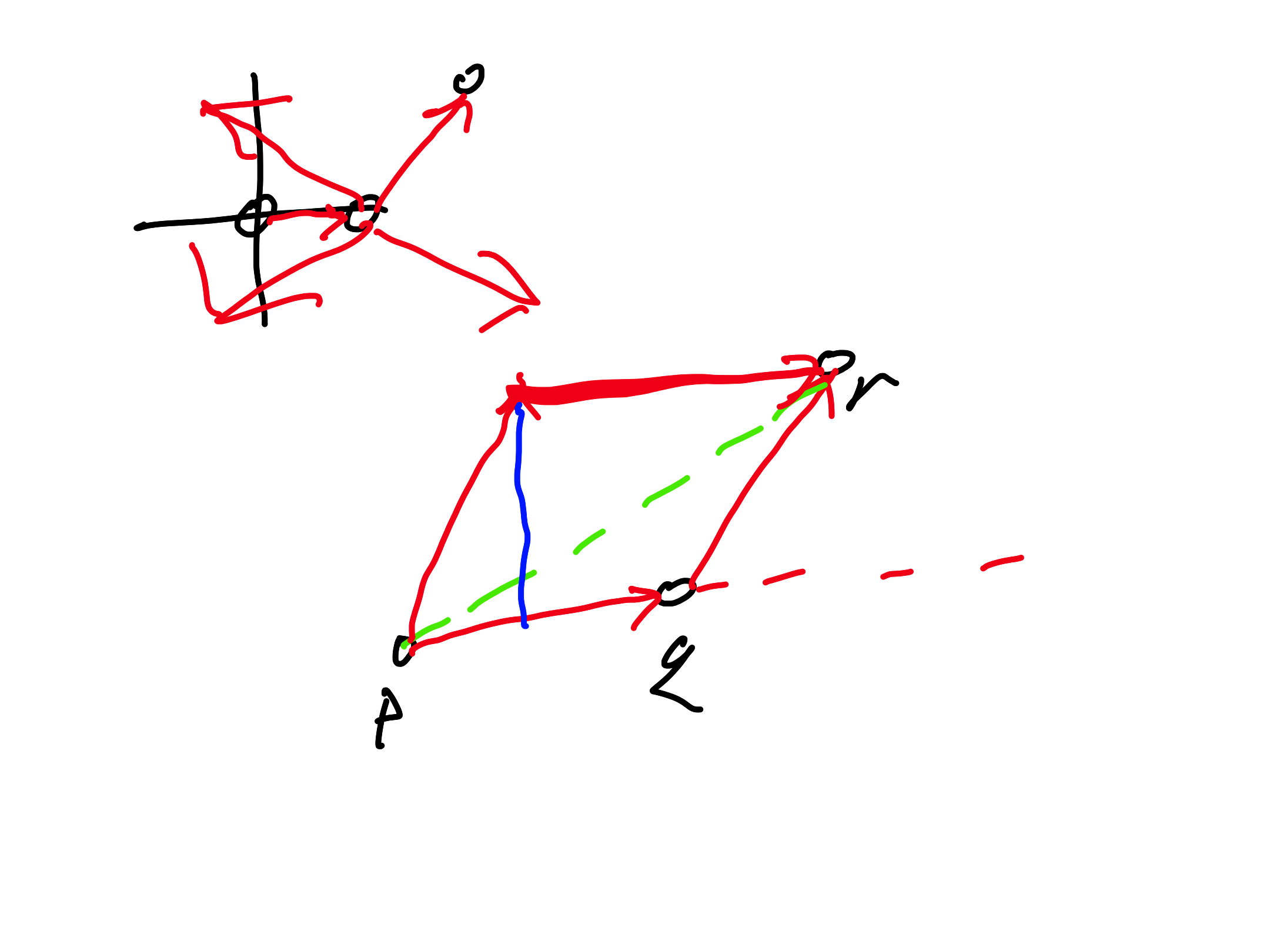
Base case:
* $p = (0, 0)$
* $q = (1, 0)$
* $r = ({r_x}, {r_y})$
* $p, q, r$ is
- a left turn if ${r_y} > 0$
- a right turn if ${r_y} < 0$
- a sequence of collinear points if ${r_y} = 0$

$$
D(p, q, r) = \begin{vmatrix}
1 & 0 & 0 \\
1 & 1 & 0 \\
1 & r_x & r_y
\end{vmatrix}
= r_y
$$

Scaling by a factor $k \ne 0$:
$$
D(kp, kq, kr) = \begin{vmatrix}
1 & k p_x & k p_y \\
1 & k q_x & k q_y \\
1 & k r_x & k r_y
\end{vmatrix}
= k^2 D(p, q, r)
$$

Translation by $(x, y)$:
$$
D(p + (x, y), q + (x, y), r + (x, y)) = \begin{vmatrix}
1 & p_x + x & p_y + y \\
1 & q_x + x & q_y + y \\
1 & r_x + x & r_y + y
\end{vmatrix}
= D(p, q, r)
$$

Rotation by $\alpha$ around the origin:
$$
D(R_\alpha(p), R_\alpha(q), R_\alpha(r)) = \begin{vmatrix}
1 & \cos(\alpha) p_x + \sin(\alpha) p_y & -\sin(\alpha) p_x + \cos(\alpha) p_y \\
1 & \cos(\alpha) q_x + \sin(\alpha) q_y & -\sin(\alpha) q_x + \cos(\alpha) q_y \\
1 & \cos(\alpha) r_x + \sin(\alpha) r_y & -\sin(\alpha) r_x + \cos(\alpha) r_y
\end{vmatrix}
$$

$$
= \begin{vmatrix}
1 & p_x & p_y \\
1 & q_x & q_y \\
1 & r_x & r_y
\end{vmatrix} \cdot
\begin{vmatrix}
1 & 0 & 0 \\
0 & \cos(\alpha) & -\sin(\alpha) \\
0 & \sin(\alpha) & \cos(\alpha)
\end{vmatrix}
= D(p, q, r)
$$

$$
D(p, q, r) = p_x q_y + q_x r_y + r_x p_y - p_x r_y - q_x p_y - r_x q_y
$$

---

### Exercise 5

Describe an algorithm which computes the intersections of a given line with a given circle in a plane.

---

### Exercise 6

You are given a set $P$ of points in the plane. Find all collinear tuples of points in $O(n^2 \log n)$ time.