---
tags: vaje, rg, mnogokotniki
hackmd: https://hackmd.io/OL5rb9iUQsiFJzSb668Tyw
plugins: mathjax
---
# Computational geometry - Tutorial 7.4.2021

---

## Polygons

### Exercise 1

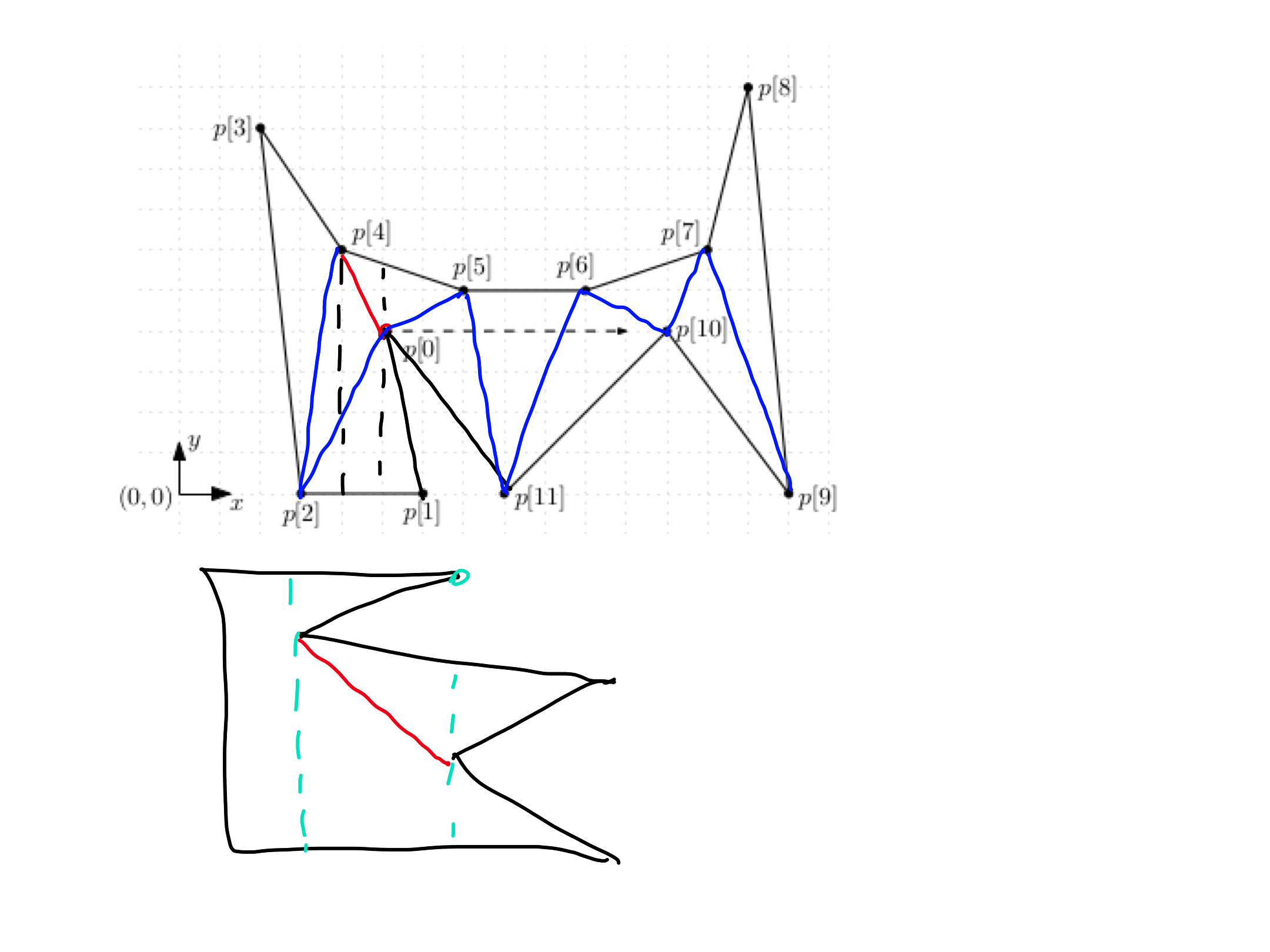
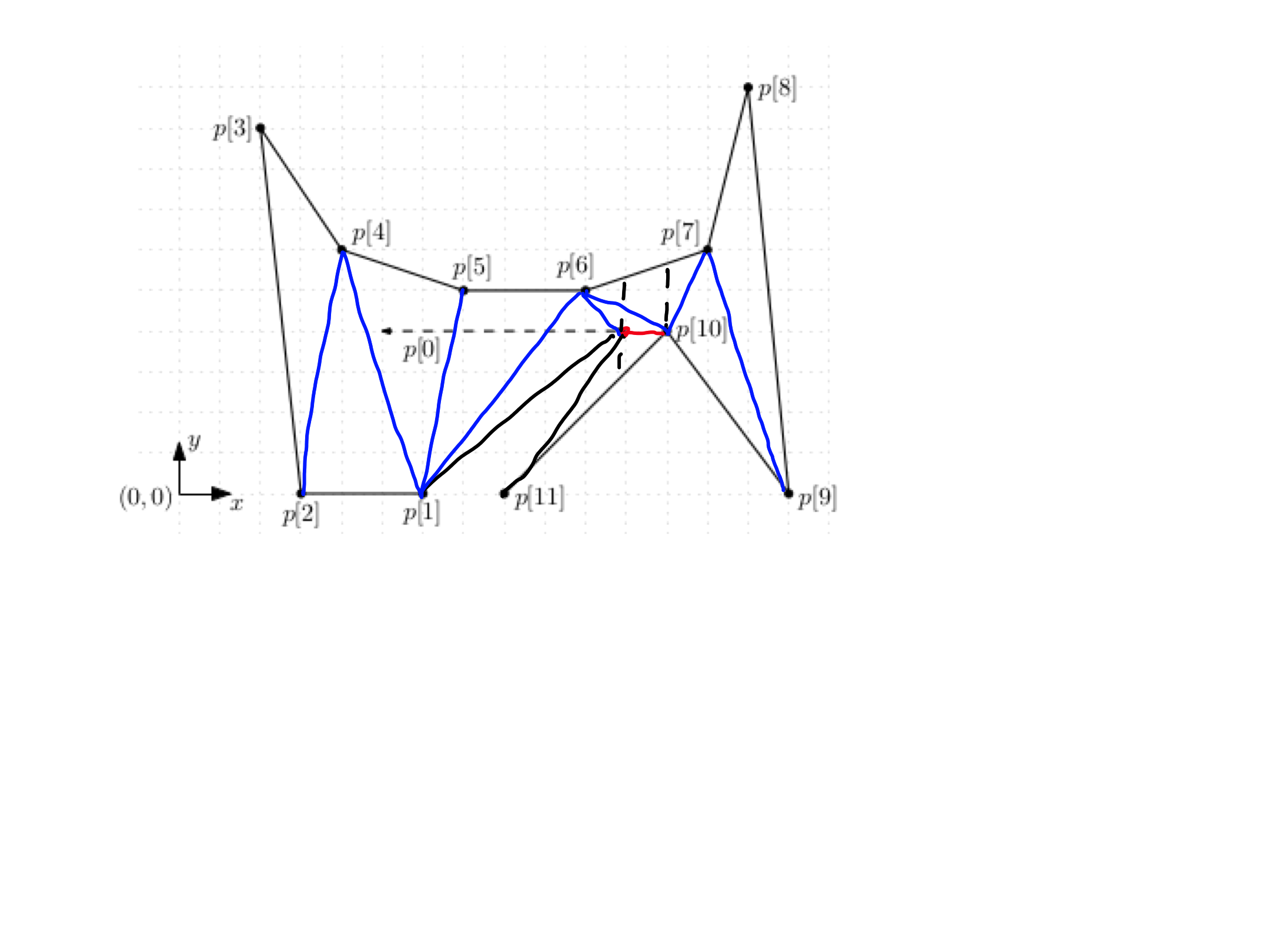
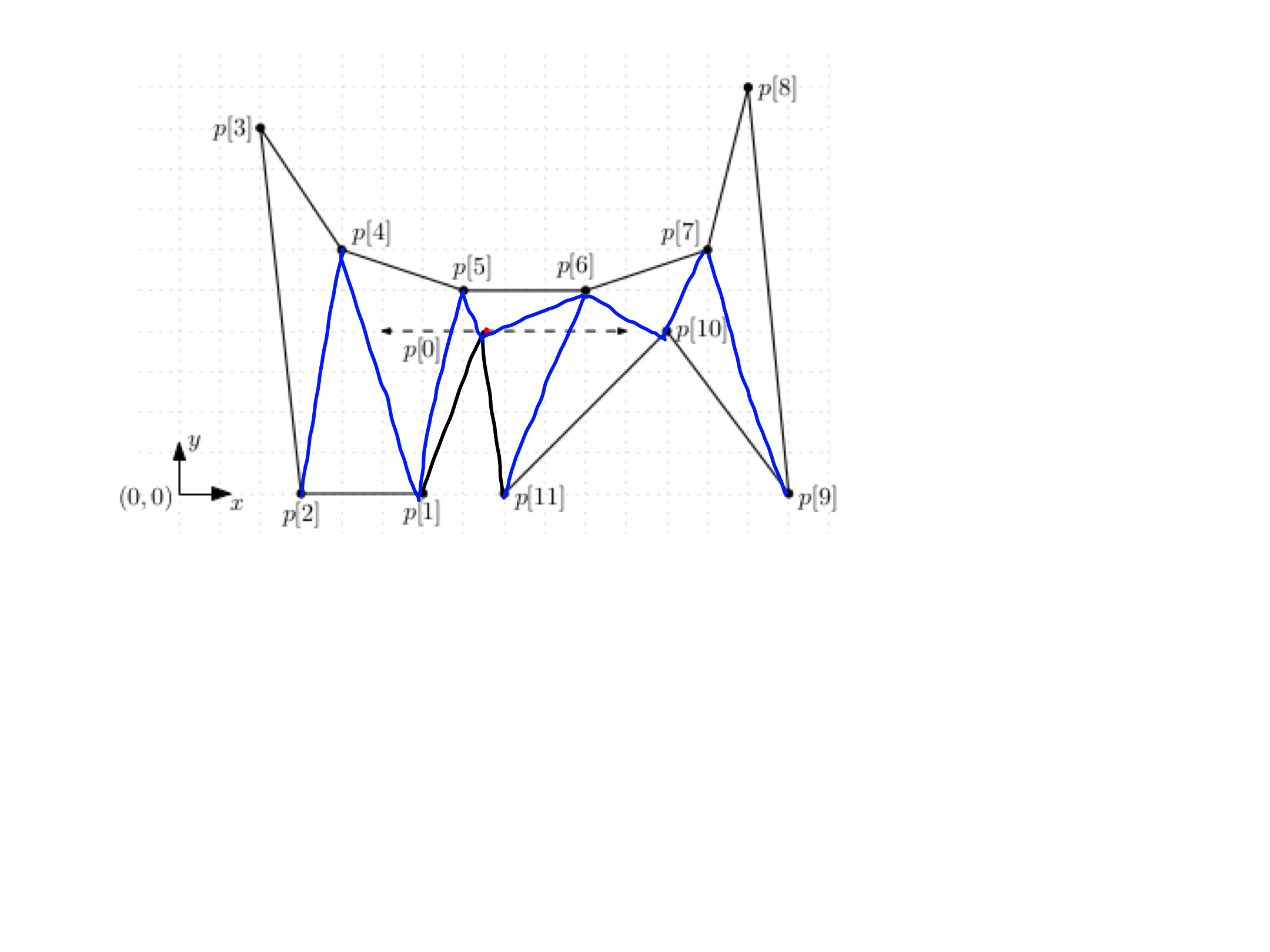
We are given a polygon with the following vertices:

$$
\begin{aligned}
p[0] &= (a,4),& \;
p[1] &= (6,0),& \;
p[2] &= (3,0),& \;
p[3] &= (2,9),& \\
p[4] &= (4,6),& \;
p[5] &= (7,5),& \;
p[6] &= (10,5),& \;
p[7] &= (13,6),& \\
p[8] &= (14,10),& \;
p[9] &= (15,0),& \;
p[10] &= (12,4),& \;
p[11] &= (8,0),
\end{aligned}
$$

where $a \in [5,11]$.

Triangulate the polygon using the algorithm from the lectures. Find $3$ values of the parameter $a$ (the vertices of the polygon should be in general position) for which the algorithms returns different triangulations. Note that the algorithm may compute the same trianguation in different ways. For the $3$ chosen values of $a$, draw three separate pictures showing the computed diagonals.


----


---

### Exercise 2

Prove or refute:

1. Let $P$ be an $x$-monotonous polygon and let $T$ be a triangulation of the polygon $P$. Then the dual graph of the triangulation $T$ is a path.
2. Let $P$ be an $x$-monotonous polygon. Then there exists a triangulation of $P$ whose dual graph is a path.
3. For each tree $D$ there exists a polygon with a triangulation having $D$ as its dual graph.
4. For each tree $D$ with maximal degree $3$ there exists a polygon with a triangulation having $D$ as its dual graph.
5. For each $n$ there exists a $n$-gon with only one triangulation.
6. There exist polygons which are monotonous in only one direction.
7. Each convex vertex of an $x$-monotonous polygon, except for the $x$-extremal vertices, is a vertex of an ear.
8. The above statement holds for *mountain polygons*, i.e., $x$-monotonous polygons with a segment for their lower polygonal path.
9. Each polygon with an even number of edges can be split into quadrangles along its diagonals.
10. The *stabbing number* of a triangulation of a polygon is the largest number of diagonals intersected by a line in the plane. There exist polygons for which each triangulations has stabbing number of order $\Omega(n)$.

----

1. Not true.

2. Not true.


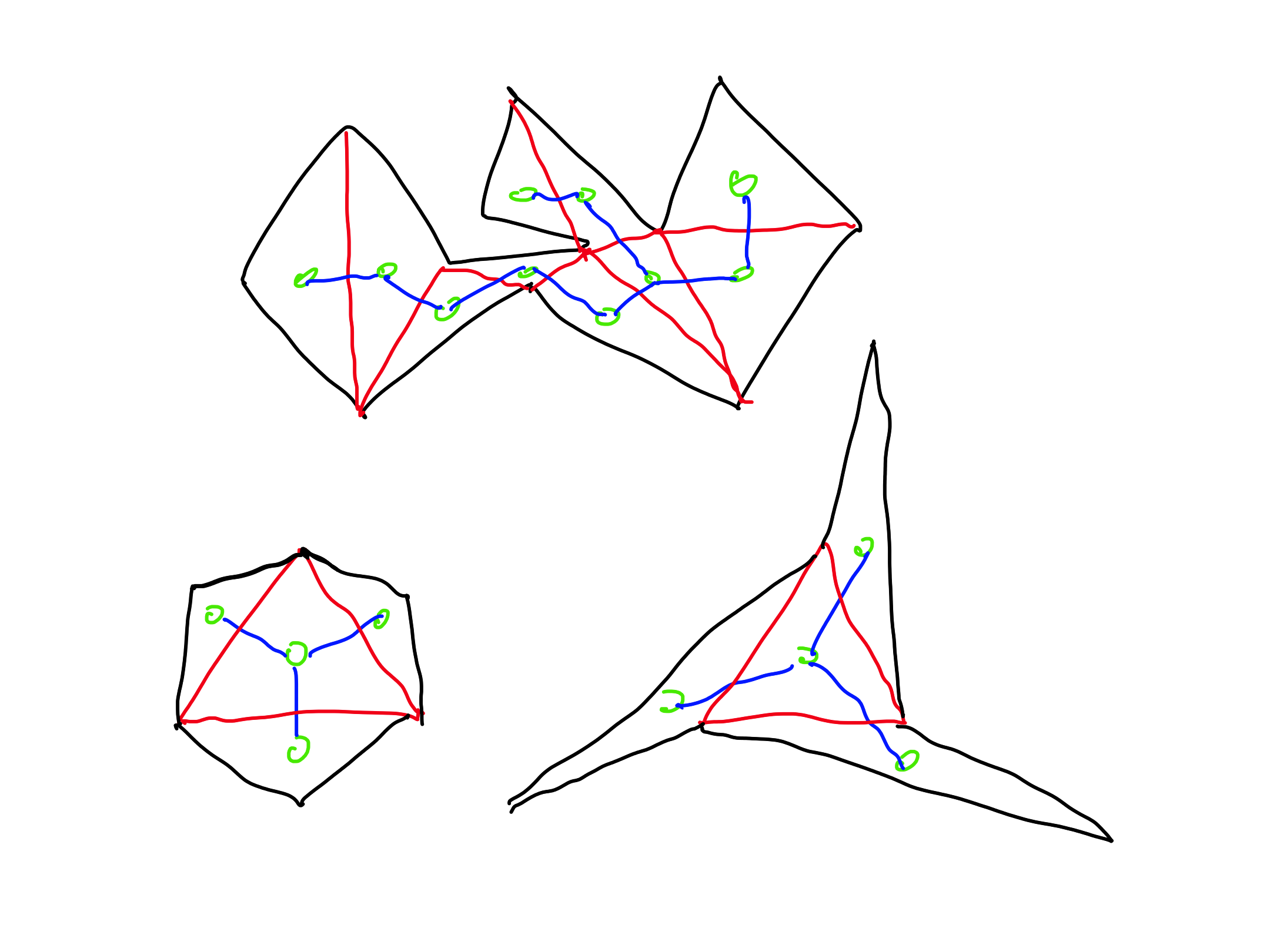
3. Not true: a tree with maximal degree at least 4 is not a dual graph of a triangulation.

4. True (with an appropriate plane drawing of the tree).


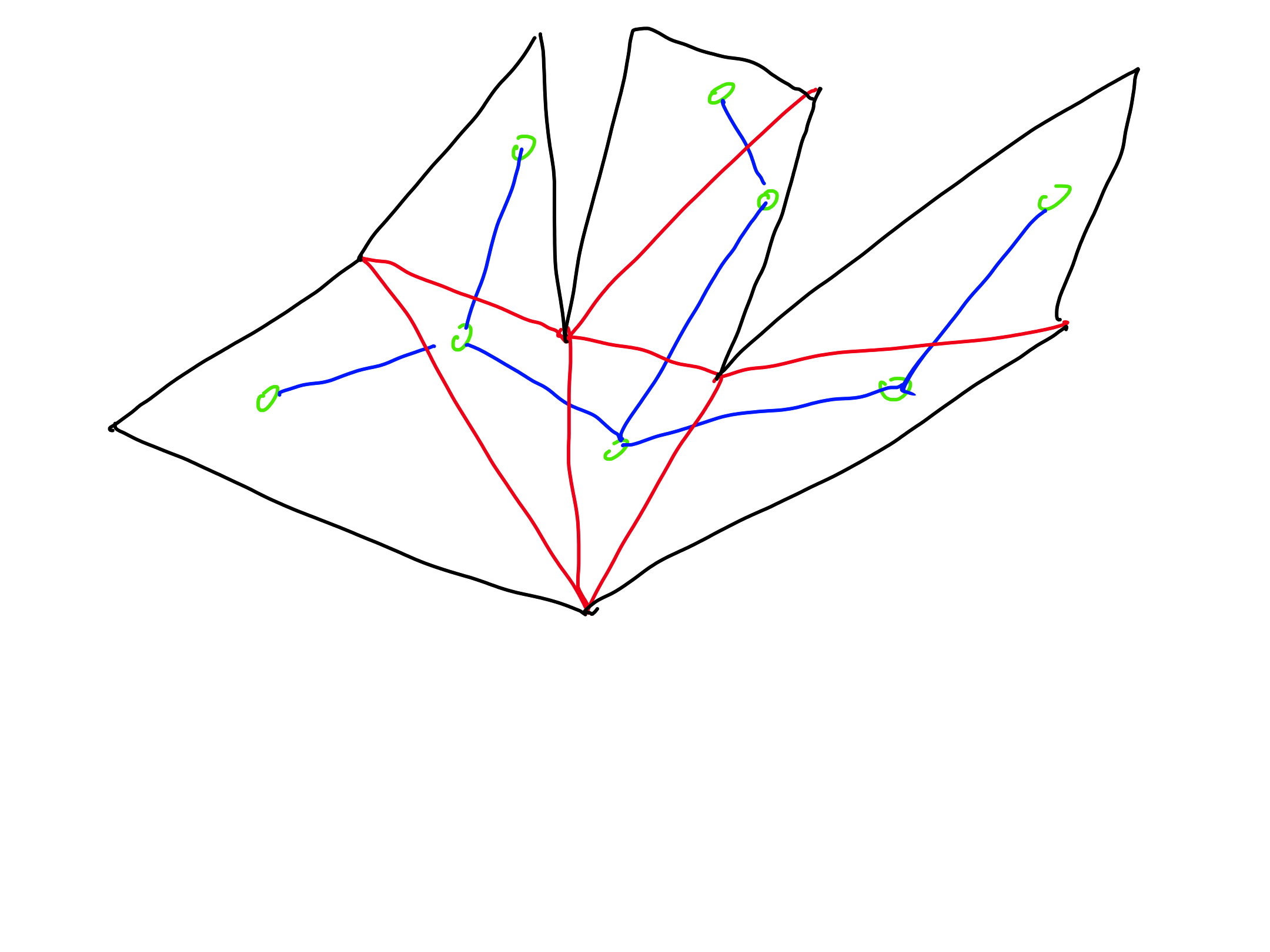
5. True.


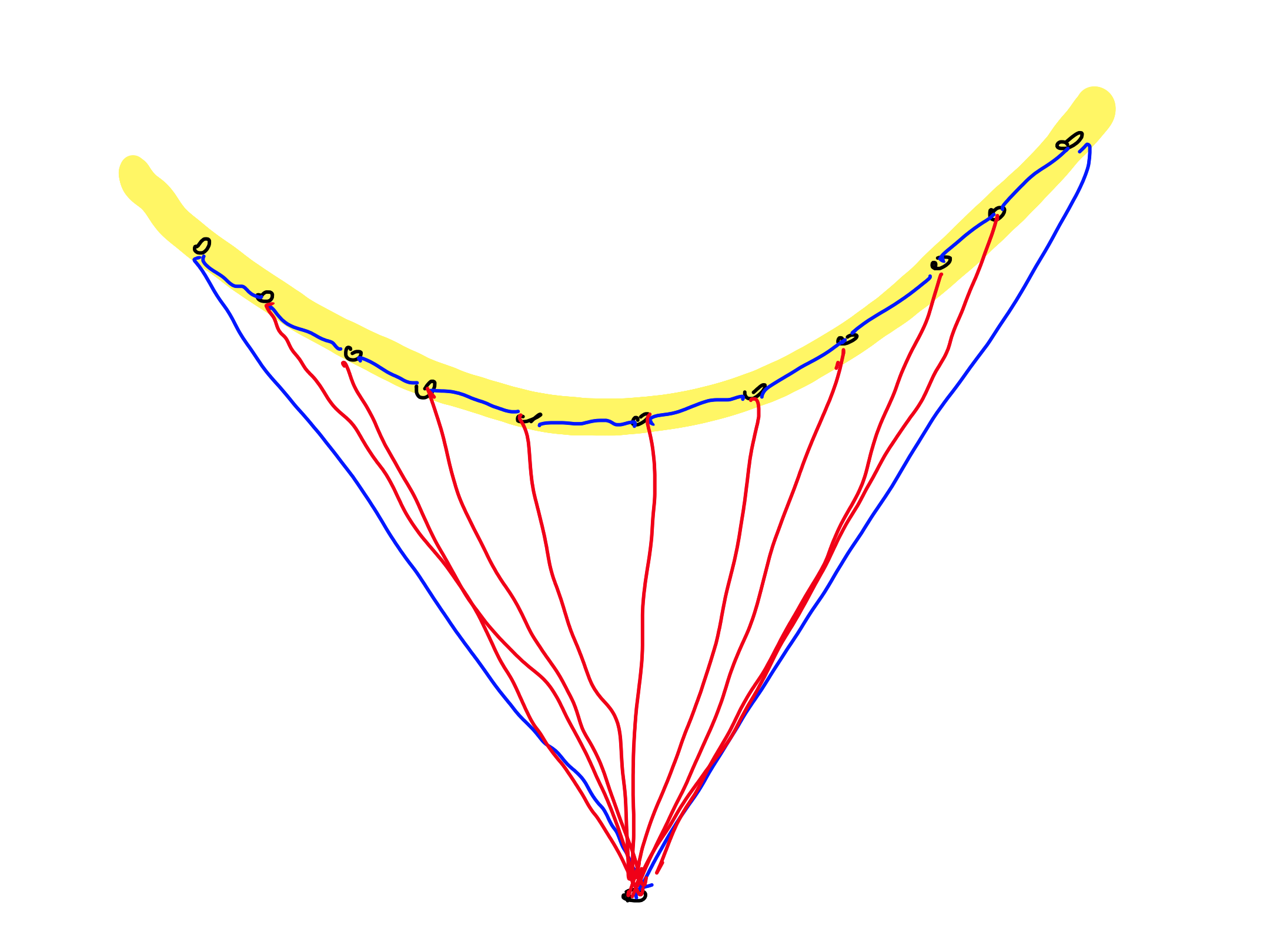
6. True.


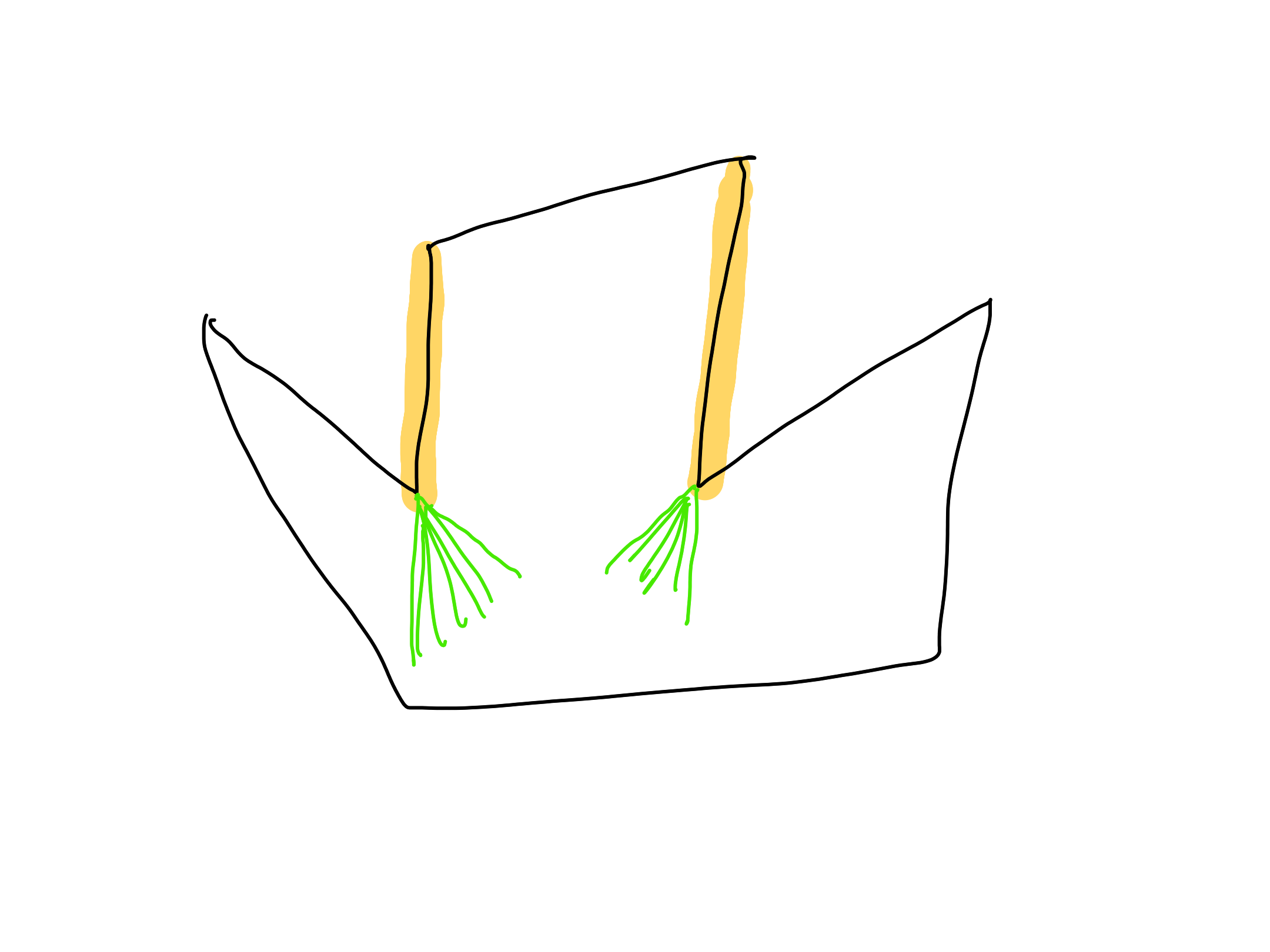
7. Not true.

8. True, since the upper polygonal path lies in entirety above the line containing the lower polygonal path.


9. Not true (see counterexample to claim 2).

10. True (see construction for claim 5).

---

### Exercise 3

Let $P$ be a polygon and let $S$ be a set of points. Describe a sweeping algorithm which returns $S \cap P$ in $O(n \log n)$ time, where $n$ is the size of the input (i.e., the number of vertices of $P$ plus $\vert S \vert$).

---

### Exercise 4

A polygon $P$ is a *star polygon* if there exists a point $p \in P$ which sees the entire polygon. We are given a star polygon $P$ and a point $p$ which sees the entire polygon $P$. Describe an algorithm which finds a triangulation of $P$ in linear time.

---

### Exercise 5

Describe an efficient algorithm for the following problem: given a polygon $P$ and a point $p \in P$ in its interior, construct the area inside $P$ which is visible from $p$.