---
robots: index, follow
tags: NCTU, CS, 共筆, 正規語言, 陳穎平
description: 交大資工課程學習筆記
lang: zh-tw
dir: ltr
breaks: true
disqus: hackmd
GA: UA-100433652-1
---
<!--
為了避免編輯器內無法正確將語法上色
1. 若使用區塊性 $$Latex$$ ，前面請加上tab
2. 要使用關鍵符號，像是[]<>，作為一般符號，不具任何用途時請用跳脫字元寫法，前面加上倒斜線
-->
正規語言--陳穎平
=====
`NCTU` `CS`
[回主頁](https://hackmd.io/s/ByOm-sFue)

[TOC]

# Syllabus
- 當15~30%
- Score
- 三考試 30%, 30%, 40%
- 基本不點名
- 沒作業
- [open course 參考](https://www.youtube.com/watch?v=Kfh7lbgPFew&list=PL82C4B8475CAC3F95)
- [筆記 參考](http://www.evanlin.com/moocs-coursera-automata-note1/)
- [學長 筆記](http://mropengate.blogspot.tw/search/label/Computer%20Science-Formal%20Language)

# Course
資訊工程理論＋正規語言
討論「計算」這件事

從三個層面討論
- automata
- computability
- complexity

是數學課

問題：只有一個符號也算符號集嗎？
答案：yes

問題：為什麼需要有空字串這個符號？有啥用？
答案：就是有用，ex: 可以當作concate連接 的單位元素

## Ch0
1. What are the fundamental capabilities and limitations of computers?
- automata (自動機)
properties of mathematical models of computation (是否可**算**)
- finite automata
- context-free grammar
- computability
- solvable vs unsolvable
- complexity
what make some problems computationally hard and others easy?
2. Nations and Terminology
- Set (without order)
- Sequences and Tuples (with order)
- Functions and Relations
- Graphs (Vertax, Edge)
- String and Language
- Boolean Logic
3. Definitions, Theorems, Proofs
4. Types of Proofs
- Construction (建構法)
- Contradiction (反證法)
- Induction (數學歸納法)
### Definition
- Set: a group of objects represented as a unit
- elements/members: objects in a set
- membership($\in$) / nonmembership($\notin$)
- subset($\subseteq\nsubseteq$)
- proper subset($\subset\not\subset$): A is a subset of B and not equal to B
- infinite set
- empty set($\emptyset$)
- Operator
- union($\cup$)
- complement($\bar{A}$)
- Venn diagram
### Sequences and Tuples
A sequence of objects is a list of these object in some order
- Order doesn't matter in a set
- tuples: Finite sequences
- k-tuple: sequence with k elements
- pair: 2-tuple
- power set
set of all subset of a SET
e.g. powerSet({0,1}) = {$\emptyset$,{0},{1},{0,1}}
- Cartesian product / cross product
- $A\times B$
- all set of first elem is a member of A and second elem is a member of B
- 
### Function and Relation
- f(a) = b
- mappping
- domain(D), range(R)
- f: D => R
- k-ary function: function with k arguments

## Ch1
### Finite Automata
- definition

$$(Q,\sum,\delta,q_0,F)$$

- DFAs (Deterministic Finite Automaton)
A deterministic finite automaton is represented formally by a 5-tuple ($Q$,$\Sigma$,$\delta$,$q_0$,$F$), where:
1. $Q$ is a finite set of states.
2. $\Sigma$ is a finite set of symbols, called the alphabet of the automaton.
3. $\delta$ is the transition function, that is, $\delta$: $Q$ × $\Sigma$ $\to$ $Q$.
4. $q_0$ is the start state, that is, the state of the automaton before any input has been processed, where $q_0$ $\in$ $Q$.
5. $F$ is a set of states of $Q$ (i.e. $F$ $\subseteq$ $Q$) called accept states.

- Computation
- $M=(Q,\sum,\delta,q_0,F)$
- string: $w=w_1w_2...w_n$
- M accepts w if:
1. $r_0=q_0$
2. $\delta(r_i,w_{i+1})=r_{i+1}$
3. $r_n\in F$
- M **recognizes language** A if $A=\{w|M\ accepts\ w\}$
:::info
A language is called a **regular language** if some finite automaton recognizes it
:::

- The Regular Operation
- Union
$A \cup B=\{x\ |\ x \in A\ or\ x \in B\}$
- Concatenation (x 後面接 y 形成新 string)
$A \circ B=\{xy\ |\ x \in A\ and\ y \in B\}$
- Star
$A^*=\{x_1x_2...x_k | k>=0 \bigwedge\forall x_i\in A\}$
:::success
The class of regular languages is *closed* under the union operation (只要兩個是RL，union 後還是RL)
:::
proof:

+ 找一部機器M來recognize他
假設$M_1$ recognize $A_1$, $M_2$ recognize $A_2$, $M$ recognize $A_1 \cup A_2$，則$M$為一台同時模擬$M_1$與$M_2$的機器，模擬時用$Q_1 \times Q_2$紀錄模擬狀態進行到哪裡，只要有任何一邊$accpet$，即為$accpet$

:::success
The class of regular languages is closed under the concatenation operation
:::
- Nondetermin (NFA)

#### Formal Definition fo NFAsism
- Deteterminism
- Nondeterminism
- 吃一個 symbol 可以去多個state
- 不吃 symbol ($\epsilon$) 也可以去下個state
- accept 就是有其中至少一個路到final state
- def
- Q is finite set
- $\Sigma$ is a finite alphabet
- $\delta = \Sigma × Q$
- $q_0 \in Q$ : start state
- $F \subset Q$ accept state (is a set)
- require:
- $r_0 = q_0$
- $r_{i+1} \in \delta(r_i, w_{i+1})$ <= different to DFAs
- $r_m \in F$

**NFAs is also a finite automata**
DFA is a specify of NFA $DFA \in NFA$ (easy to understand)
**But NFA is also belongs to DFA** -> <span style="color:red;">$NFA \equiv DFA$</span>
Proof: All NFA can construct to DFA

把NFA的樹打平，也就是把每層的狀態集打成每種狀態 => New set = P(Q)*
如些可以解決一個symbol map到多個state的問題
new δ(R,a) = union of δ(R,a)
new q0 = {q0}
new F = all set of F which has F
** E()

*: [P() is a power set, e.g. S{a,b}, P(S) = {}, {a}, {b}, {a,b}]

正確性證明:
For DFAs, define *extended* transition function
$$\delta^*: Q × \Sigma^* -> Q$$
Let $w = xa$, $w,x \in \Sigma^*$, $a \in \Sigma$, and $|w| >= 1$,
$\delta^*(q,\epsilon) = q\\
\delta^*(q,w) = \delta(\delta^*(q,x),a)$
:::info
A language is regular <=> DFA recognizes it
:::
Concatenation close 證明:
- use two NFAs
- 將第一個 NFA 的 end state 都用 $\epsilon$ 指向 第二個 NFA 的 start state
:::success
$A^*$ is close in RL
:::
將 NFA 中的 end state 都用 $\epsilon$ 指向 start state
做完後再新增一個 start state 用 $\epsilon$ 指向原來的 state state(用以 match $\emptyset$)
### Regular Expression
R is regular expression if R is:
1. a for some a in the alphabet $\sum$
2. $\epsilon$
3. $\emptyset$
4. ($R_1\cup R_2$)
5. ($R_1 \circ R_2$)
6. ($R_1^*$)

- $R^+$: 1 or more concatenation of strings from R
- $R^+\cup\epsilon=R^*$
- $R^k$: concatenation of k R's with each other

:::info
A language is regular <=> some regular expression describes it
:::
- language is described by a RE, then it is regular
- convert RE into an NFA
1. R = a => L( R ) = {a}
2. R = $\epsilon$ => L( R ) = {$\epsilon$}
$N=(\{q\},\sum,\delta,q,\{q\})$
3. R = $\emptyset$ => L( R ) = $\emptyset$
$N=(\{q\},\sum,\delta,q,\emptyset)$
4. R = $R_1\cup R_2$
5. R = $R_1\circ R_2$
6. R = $R_1^*$
- DFA to RE
- using GNFA
- GNFA is a finite automata with RE on the arrow
- DFA -> GNFA -> RE
### [GNFA](https://en.wikipedia.org/wiki/Generalized_nondeterministic_finite_automaton)
- nondeterministic (like NFA)
- arrows may have any regular expression
$$(Q,\sum,\delta,q_{start},q_{accept})$$
1. Q: finite set of states
2. $\sum$: input alphabet
3. $\delta:(Q-\{q_{accept}\})\times(Q-\{q_{start}\}) -> R$: transition function
4. $q_{start}$: start state
5. $q_{accept}$: accept state

- For convenience:
- start state 的箭頭只會往外射，沒有箭頭會射回 start state
- 只有單一個 accept state，只會有箭頭射向它，不會有射出的箭頭
- start state 跟 ac state 一定不同
- DFA -> GNFA
- 加入 start state 和 end state
- 把 start state 用 $\epsilon$ 指向 DFA 的 start state
- 把 DFA 所有的 end state 用 $\epsilon$ 指向新的 end state
- 把有多個 member 的箭頭全部各自拉成一個箭頭
- 若有 state 互相間沒有箭頭連接，新增 $\emptyset$ 的箭頭將之連接
- 每次拔一個點，拔法: $\{入度\}\circ(自己的環)^*\circ\{出度\}$
### Pumping Lemma
正規語言一定要滿足 pumping lemma，但滿足 pumping lemma 的不一定是正規語言
is regular language => meet pumping lemma
:::info
if A is a regular language, then there is a number p (pumping length) where, if s is any string in A of length at least p, then s may be divided into three pieces, s = xyz, satisfying the following conditions:
1. for each i >= 0, $xy^iz\in A$
2. |y| > 0
3. |xy| <= p
:::
反證法 + pumping lemma 證明某規則不是 regular language
### Closure Properties
- Union: $A ∪ B$
- Concatenation: $A\circ B$
- Star: $A^*$
- Intersection: $A ∩ B$
- Complement: $\bar{A}$ (i.e., $Σ^∗ − A$);
- Difference: $A-B = A∩\bar{B}$
- Reversal: $A^R$
- Homomorphism: $h(A)$
- Inverse Homomorphism: $h^{-1}(A)$

### [Myhill-Nerode Theorem](http://mropengate.blogspot.tw/2015/04/formal-language-ch5-myhill-nerode.html)
- Indistinguishable (不可區分)
- $z \in Σ^*$ 且同時 $xz,yz\in L$ 或同時 $xz,yz\not\in L$
- => $x \equiv_L y$
- 等價關係
- 從DFA的角度來看，不可區分就是兩個不同字串xz和yz進入機器M時，最後都會停在同一個狀態 (AC or not AC)
- Myhill-Nerode Theorem
- 如果一個語言L是正則的話，則$\equiv_L$的等價類數目是有限的(若且唯若)
- 取代 pumping lemma 成為檢查 RE 的最好方法
### Minimization of DFAs

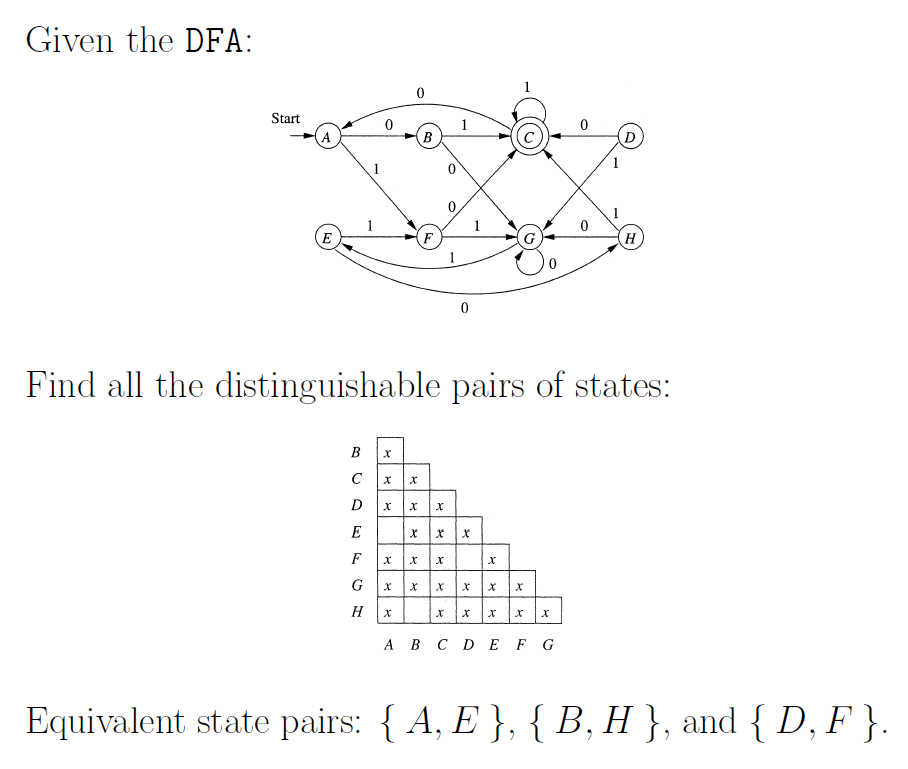
## Ch2 Context-Free Grammar (CFG)
CFG include *all* regular language
### CFG
- $L(G)$: language of grammer
- variable -> terminals
- start variable
- parse tree (解析樹)
- A → 0A1 & A → B => A → 0A1 | B
:::info
Context-Free Grammar (CFG)
$$(V,\Sigma,R,S)$$
- $V$: finite set, called **variables**
- $\Sigma$: finite set, disjoint from V, called **terminals**
- $R$: finite set of **rules**
- $S\in V$: start variable
:::
- $uAv$ *yields* $uwv$ ($uAv\Rightarrow uwv$) if $A\to w$
- $u$ derives $v$($u\Rightarrow^*v$) if $u\Rightarrow u_1\Rightarrow u_2\Rightarrow...\Rightarrow v$
- L(G) is $\{w\in\sum^*\mid S\overset*\Rightarrow w\}$
#### Design a CFG
1. Divide & Conquer
2. Regular Experesion (convert to DFA)
每個 $stateA \overset{s}\to stateB$ => $A \to tB$
3. 處理須記憶個數的
4. recursive

### Ambiguity(模糊性)
字串對應到文法時，有兩種以上的對應方式
一個 grammar 可以用兩種以上的方式產生同一個字串
- two different parse trees $\not=$ different derivations (?)
- **leftmost derivation**: 每次 derivation 都是最左邊的 variable 被換掉
:::info
A string $w$ is derived **ambiguously** in context-free grammar G if it has two or more different leftmost derivations.
Grammar G is **ambiguous** if it generates some string ambiguously.
:::
- 有時一個 Ambiguiguous Grammar 可以找到一個 unambiguous grammar 產生同一種語言
- **Inherently ambiguous(絕對曖昧)**: 一定找不到對應的 unambigous grammar 產生同一種語言

### Chomsky Normal Form
all CNF is context-free, and all context-free can convert to CNF
:::info
Chomsky normal form
$A\to BC$ 一個符號變成兩個非起始符號
$A\to a$ 一個符號變成一個結束符號
$S\to\epsilon$ 起始符號可變空字串(如果語言本來包含空字串)
:::
- $CFG\to CNF$
- start variable 只會在左邊 => 新增一個 start variable
- 除了 start 外不能有 $S\to\epsilon$ => 將所有 $\epsilon$ 拔掉
- 不能有 terminal 跟 variable 合用 => 遇到了話將 terminal 拉出來在開一個 veriable (V -> a)
- 指向的 variable 一定是兩個 => 遇到只指向一個 veriable 的，將那個 variable 指向的下一個東西拿來取代它

### Pushdown automaton (PDA)
Control read input, and if necessary, push or pop stack
- stack => it can memory
:::info
pushdown automaton
$$(Q,\Sigma,\Gamma,\delta,q_0,F)$$
- Q: set of states
- $\Sigma$: input alphabet
- $\Gamma$: stack alphabet
- $\delta$: $Q\times\Sigma_\epsilon\times\Gamma_\epsilon\to P(Q\times\Gamma_\epsilon)$ transition function
- $q_0\in Q$: start state
- $F\subseteq Q$: accept state
:::
:::success
CFG $\Leftrightarrow$ PDA recognizes it
:::
- CFG -> PDA
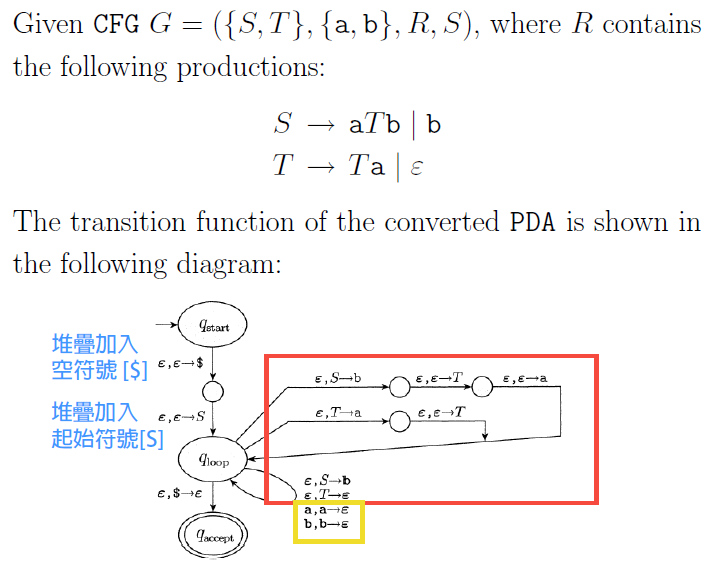
- PDA -> CFG
- modify PDA
- single accept state, $q_{accept}$
- empty it's stack before accept
- doesn't do push and pop at the same time

RL <= context free language(CFG & PDA)
可是 context-free languages 還是不能包含所有 language => 還有更大的集合
### Non-context-free languages
### Pumping lemma for context-free languages
s is any string in A of length at least p, s = uvxyz =>
1. for each i >= 0, $uv^ixy^iz\in A$
2. $|vy| > 0$
3. $|vxy| <= p$

$$\{x^py^pz^p\}$$
is not context-free

#### Ogden's Lemma for CFL's
If A is CFL, if s in string in A of length at least p, select any p or more *positions* to be distinguished, the ns may be divided into five pieces, s = uvxyz =>
1. for each i >= 0, $uv^ixy^iz \in A$
2. vy has at least one distinguished positions
3. xyz has at most p distinguished positions

e.g. $L=\{a^ib^jc^kd^l | i=0 or j=k=l\}$
L is not CFL

### [CYK](https://goo.gl/6lnBjG)
有沒有好心人願意幫我寫 XD

## Ch3 圖靈機
### 定義
Finite control + unlimited and unrestricted memory
1. 在 tape 上讀寫
2. 移動 head 向左或向右
3. tape 無限長
4. Reject and accept immediately
- $B=\{w \# w | w\in\{0,1\}^*\}$

- $(Q, \Sigma, \Gamma, \delta, q_{0}, q_{accept}, q_{reject}), \text{where }Q, \Sigma, \Gamma\text{ are all finite sets}$
1. Q is the set of states
2. $\Sigma$ is the input alphabet **not containing** the **blank symbol** $\sqcup$
3. $\Gamma$ is the tape alphabet, where $\sqcup \in \Gamma$ and $\Sigma \subseteq \Gamma$
4. $\delta$ : $Q \times \Gamma \rightarrow Q \times \Gamma \times \{L, R\}$ is the transition function
5. $q_{0}$ $\in$ Q is the start state;
6. $q_{accept}$ $\in$ Q is the accept state;
7. $q_{reject}$ $\in$ Q is the reject state.
- configuration
- 當前 state
- 當前 tape 內容
- 當前 head 位置

用 $uqv$ 來表示當前 TM 的 configuration，把 tape 切成 $uv$ 兩段 head 位置為 $v$ 的第一個字元，$q$ 則是當前 state
- 如果一台 TM 可以合法地從 configuration C1 走到 configuration C2 則稱 C1 **yields** C2
- Special configuration
- **start** configuration: $q_{0}w$
- **accepting** configuration: the state is qaccept
- **rejecting** configuration: the state is qreject
- **halting** configuration: accepting and rejecting
- TM accepts input $w$ 條件
- 存在 C1, C2..., Ck
1. C1 是 start configuration
2. Ci yields Ci+1
3. Ck 是 accepting configuration
- All strings that M accepts = the language of M = the language recognized by M = L(M)
### 變形
#### [k-tape TM](https://goo.gl/b2IiHb)
- $\delta$ : $Q \times \Gamma^{k} \rightarrow Q \times \Gamma^{k} \times \{L, R, S\}^{k}$
- 每一個 k-tape TM 都有一個等價的 single-tape TM
1. 先將 k 個 tape 的內容抄到一條 tape 上，並將每條 tape 的內容用 # 隔開，每條 tape 的 head 標記一個點 (virtual head)
2. 模擬每一步，從第一個 # 開始往右掃，如果遇到virtual head，就看對應的 tape 遇到該狀態要如何轉移，並更新 virtual head 位置，直到第 k + 1 個 #
3. 若有 virtual head 右移指到 #，則將右邊的所有內容向右搬一格，virtual head 設為空
- Turing-recognizable $\Leftrightarrow$ some k-tape TM recognizes
#### [Nondeterministic TM](https://goo.gl/b3RFCZ)
- $\delta$ : $Q \times \Gamma \rightarrow P(Q \times \Gamma \times \{L, R, S\})$
- 每一個 nondeterministic TM 都有一個等價的 deterministic TM
1. tape 1 存 input，tape 2 和 tape 3 設為空
2. 將 tape 1 的值複製給 tape 2
3. 用 tape 2 來模擬其中一個 branch 的狀態，並將可以走到的位置記錄到 tape 3 中，深度優先走訪若遇到 accepting configuration 就 accept input，若 reject 或該 branch 不合法或 tape 3 為空就跳到第 4 步
4. 往 tape 3 的下一個位置，跳回第 2 步繼續模擬下一個 branch
- Turing-recognizable $\Leftrightarrow$ some nondeterministic TM recognizes
- decidable $\Leftrightarrow$ some nondeterministic TM decides
#### Enumerators
- 無 input，一直枚舉字串
- Turing-recognizable $\Leftrightarrow$ some enumerator enumerates
- enumerator 轉 TM
- 跑 enumerator 生成的字串與 input 比較，若相同則 accept
- TM 轉 enumerator
- 忽略 input，以 s1, s2..., si 當作 input 在 TM 上跑 i 步，若有字串 accept 則輸出該字串，i 從 1 遞增

### 演算法
#### Hilbert's Problems
> Find an algorithm to determine whether a given polynomial Diophantine equation with integer coefficients has an integer solution.

Define the term algorithm by using
- Church: $\lambda$-calculus
- Turing: Turing machines

Turing-recognizable? Turing-decidable?
- $D = \{\ p\ |\ p \text{ is with an integral root} \}$
- $D1 = \{\ p\ |\ p \text{ is over x with an integral root} \}$
#### Terminology for Describing TM
- **formal** description: Spells out in full the Turing machine's states, transition function, and so on
- **implementation** description: Describes the way that the Turing machine moves its head and the way that it stores data on its tape
- **high-level** description: Describes an algorithm

## Ch4 Decidability
不 accept 不代表 reject
$\rightarrow$ Decidable: 不是 accept 就會是 reject (language 外的都是 reject，沒有無窮的)
### decidable language
#### DFA example
- $A_{DFA} = \{<B,w> | \text{B is in DFA that accept string w}\}$: B 是否可接受字串 w
- 證明：建一個可以 decided $A_{DFA}$ 的 TM
- $A_{NFA}$: 轉換為 $A_{DFA}$
- $A_{REX}$: 轉換為 $A_{DFA}$
- $E_{DFA} = \{<A> | \text{A is a DFA and L(A)=0}\}$
- 這部 TM 中的 DFA 不會 accept 任何字串
- 證明，建一部 TM T
- T 吃入 DFA (的 code)
- 從 start state 一直往下走，走過標記
- 直到走到無法再走下去
- 若所有的標記中有 accept state 則 T 回傳 reject，反之 accept
- $EQ_{DFA}=\{<A,B> | \text{A and B are DFA, and L(A)=L(B)}\}$
- 吃入兩個 DFA，確認是否相同的
- proof idea: 建構非交集的地方 => 輸出 $E_{DFA}$ 的結果
- $L(C) = (L(A)\ ∩\ \overline{L(B)}\ \cup\ \overline{L(A)}\ ∩\ L(B))$
- 分別建出每個DFA後就可以判斷$L(A)$和$L(B)$是否相等

#### Context-free exaple
- $A_{CFG}$: 檢查字串 w 是否符合此 context-free B
- $A_{CFG}=\{<G,w> | \text{G is a CFG that generates string w}\}$
- 轉換成 Chomsky normal form
- 只要測試有限多次(2n-1)，就可以問出 w 是否 accept
- $E_{CFG}$ (PDA 形式)
1. 找到 terminal 並打勾
2. 若右邊的部分全部被打勾，則將左邊打勾
3. 左邊有打勾的，回到右邊打勾
4. 遞迴
5. 最後檢查 start variable 有無打勾
6. 有打勾則 language 不為空，reject
- $EQ_{CFG}$: **UNDECIDABLE**

### Halting Problem
想確認 turing-recongnizable 和 decidable 中間是否有 set (or Turing-recognizable == decidable)
- $A_{TM} = \{(M, w) | \text{ M is a TM that accept w}\}$
1. recognizable
- 三種可能（accept, reject, 無窮迴圈）

利用反證法找到在 decidable 外的 machine，證明decidable $\subset$ Turing-recognizable
Run a Program D

D( input <M> )                         // M is a TM
    Run H on input <M,<M>>             // 讓M查看自己(<M>可以理解為 M 的 code)
    Output opposite of what H output   // D 回傳 H 的相反值
H( input <M,w> )
    accept if M accepts w
    reject if M "does not" accept w

所以把 M 丟入 D 後：
    accept: 當 M 不接受 M
    reject: 當 M 接受 M
若再把 D 丟入 D：
    accept: 當 D 不接受 D
    reject: 當 D 接受 D
    矛盾(答案報錯) => ATM 不存在

- **$A_{TM}$ 真的在 decidable 外面**

#### 到底 recognizable 是否是全部 language
- 發現 recognizable 外面還有東西 !!
- 算數量方式 (Diagonalization Method) 證明
- 定義可以判斷大小的方式
- 因為 language 是無限大的 set，所以定義的方式需要可以比較無限大的大小
- using one-one matching
- one-to-one: $x \not= y \Rightarrow f(x) \not= f(y)$
- onto: $\forall b \in B, \exists a \in A, f(a) = b$
- countable
- 有限大
- 可跟 自然數 one-to-one & onto
- mapping 方式：
- N(recognizable) < N(\<TM\>) < N(string) < N(language)
- N(recognizable) < N\(TM\): 多個 TM 可能會便是到同樣的 recognizable language
- N(\<TM\>) < N(string): TM(的 code)，也是 string 組成的，所以會 <= N(string)
- N(string) < N(language): language 是 string 的集合

### Turing-UnRecognizable
#### 舉例一：$\overline{A_{TM}}^*$
- co-turing-recognizable
co-XXX 代表是 XXX 的 complement
- 想證明一個 language 是 decidable 時 $\Leftrightarrow$ 同時是 turing-rec 跟 co-turing-rec
- $\Leftarrow$:
分別可以用 turing-rec 和 co-turing-rec 做出兩個 recognizer M1 和 M2，讓 x 同時跑 M1 和 M2(bfs like 的做法，丟入 queue裡)，若有人找到答案則同時停止，就做出 decider 了
- $\Rightarrow$:
- 得到 $\overline{A_{TM}}^*$ 就是在 turing 外的 language(**turing-unrec**)
- 已知 $A_{TM}$ 是 reco...，若 $\overline{A_{TM}}$ 也是 reco...，那 $A_{TM}$ 就是 decidable，可是剛剛已經證明過 $A_{TM}$ 是 undecidable

#### 舉例二

## Ch5 Reducibility
reduces: 將一個問題包裝/解構成另一個問題
A reduces to B => used B's solution to solve A
**BUT reduce 不會減少問題難度**
- B is disabled => A is disabled
- A is undisabled => B is undisabled
- When A reduceable to B
- solving A cannot be harder than solving B
- B is decidable => A is decibable
- A is undecidable => B is undecidable
### Undecidable problems from Language Theory
- $HALT_{TM}=\{<M,w>|\text{M is a TM and M halt on input w}\}$
- undecidable
- [證明](https://zh.wikipedia.org/wiki/停机问题)
- R 吃入 M 和 w，輸出 w 是否會在 M 上停止(不出現無限迴圈)
- H(M,w): R輸出停止了話，就輸出w在M上的結果，反之輸出 reject
- 若 R 是 decidable，則會出現 $A_{TM}$ 是 decidable 這樣與前面矛盾的狀況
- $E_{TM}=\{<M>|\text{M is a TM and L(M)=} \phi \}$
- [證明](https://cs.stackexchange.com/questions/53836/etm-undecidability)
- 假設 R 是一個可以 decide $E_{TM}$ 的 TM
- 建立一個 S，吃入 <M,w>
- 用 <M,w> 建立機器 $M_1$
- $M_1$ 吃入字串 x
- $x \not= w$ reject
- 不然就輸出 x 在 M 上的結果
- S 輸出 $R(<M_1>)$ 的相反結果
- 若 R 是 decidable，則會出現 $E_{TM}$ 是 decidable 這樣與前面矛盾的狀況 (不懂??????)
- $REGULAR_{TM} = \{ <M> |\ \text{M is a TM and L(M) is a regular language}\}$
- 假設 R 是一個可以 decide $REGULAR_{TM}$ 的 TM
- 建構 S 輸入 <M,w>
- 建構 $M_2$
- $M_2$ 輸入 x
- 若 $x = 0^n1^n$ accept
- 反之輸出 M(x)
- 在 R 上跑 $<M_2>$
- 輸出 $R(<M_2>)$
- $EQ_{TM}$
- 建一個 R decide $EQ_{TM}$
- 建一個 S input M
- R input <$M$,$M_1$>，$M_1$ reject all input
- S output R(<$M$,$M_1$>)

### [Rice theorem](https://foreseeable.github.io/2015/11/04/Ricestheorem/)
1. P 是 nontrivial
2. 只要 $L(M_1) = L(M_2)$，則 $<M_1>\in P \Leftrightarrow <M_2>\in P$

- [較完備的 doc](http://blog.csdn.net/baimafujinji/article/details/50179715)
- nontrivial(非平凡):
- 設 P 為一 language set，存在圖靈機 $M_1$ $M_2$，使得 $L(M_1)\in P$ and $L(M_2)\not\in p$
- P 包含了某些圖靈機形成的語言，但不包含所有的
- 有些 TM reco 在 P 裡，也有些不在

- $EQ_{TM}=\{<M_1,M_2> | M_1 \text{and } M_2 \text{are TMs and } L(M_1)=L(M_2)\}$
- $EQ_{TM}$ is undecidable
- Pf: 寫一個 S 吃入 TM\<M>，
1. Run R 來比對 $M, M_1$，其中 $M_1$ reject all input
2. S 輸出 R 的比對結果

### Computation history
- 從 start 一直走到結束的紀錄過程就是一個 computation history
- $C_1,C_2,...,C_n$ 如果 $C_1$ 是 start，$C_n$ 是 end，過程的轉移是合法的，就叫做 accepting computation history
- rejecting CH: 有限長度的 CH 是不存在的
- M accept w 代表 w 跑在 M 上的 history 是 accepting CH
- LBA(linear bounded automaton): 一個 TM 會動態限制長度，再決定跑 w 後，會限制長度就是 N(w) (再跑 w 時，N(w)以外的部分都是不重要的)
- 可以 handle 所有 CFL
- 介於 TM 和 PDA 間
- 跑 LBA 的所有可能數： $N(q states)\times N(n positions)\times N(g)^N(n)$ => 一定有一個 timeout
- $E_{LBA}$ 是 undecidable
- 做一個 S 只會 accept 在 M 會 accept w 的狀況下
- 其他的狀況都 reject
:::info
你有能力檢查一件東西是不是你想要的，和，你想要的東西是否存在，是完全不同的命題
:::
藍字是 decidable
<style type="text/css">
.tg {border-collapse:collapse;border-spacing:0;}
.tg td{font-family:Arial, sans-serif;font-size:14px;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg th{font-family:Arial, sans-serif;font-size:14px;font-weight:normal;padding:10px 5px;border-style:solid;border-width:1px;overflow:hidden;word-break:normal;}
.tg .tg-1rg7{color:#3531ff;vertical-align:top}
.tg .tg-baqh{text-align:center;vertical-align:top}
.tg .tg-yw4l{vertical-align:top}
.tg .tg-zlvv{color:#3531ff;text-align:center;vertical-align:top}
</style>
<table class="tg">
<tr>
<th class="tg-yw4l"></th>
<th class="tg-yw4l">A</th>
<th class="tg-yw4l">E</th>
<th class="tg-yw4l">EQ</th>
</tr>
<tr>
<td class="tg-yw4l">DFA</td>
<td class="tg-zlvv">A_DFA</td>
<td class="tg-1rg7">E_DFA</td>
<td class="tg-1rg7">EQ_DFA</td>
</tr>
<tr>
<td class="tg-yw4l">PDA</td>
<td class="tg-zlvv">A_CTG</td>
<td class="tg-1rg7">E_CTG</td>
<td class="tg-yw4l">EQ_CFG</td>
</tr>
<tr>
<td class="tg-yw4l">LBA</td>
<td class="tg-zlvv">A_LBA</td>
<td class="tg-yw4l">E_LBA</td>
<td class="tg-yw4l">EQ_LBA</td>
</tr>
<tr>
<td class="tg-yw4l">TM</td>
<td class="tg-yw4l">A_TM</td>
<td class="tg-yw4l">E_TM</td>
<td class="tg-baqh">EQ_TM</td>
</tr>
</table>

- $All_{CFG}$ is undecidable
- 建一部 PDA
- 一樣先建 configuration，只是偶數對的方向相反的建

### Post correspondence problem (PCP)
想像有一堆骨牌，骨牌呈現一個分數，上下各一個字串，問是否可能湊出上面跟下面的字串最終相等？
=> undecidable: 任意給你，很難分辨到底有無辦法 match

### Mapping Reducibility

## Ch7 Complexity
### Time Complexity
:::info
Desideable: Computationally solvable.
這是理論還是真實的呢？
:::
- Complexity
- 時間
- 記憶體
- 其他資源
-
### Measuring Complexity

只講 decidable
- asymptotic analysis
- Big-O, Small-O

# Exam:
> ◢▆▅▄▃-崩╰(〒皿〒)╯潰-▃▄▅▆◣
> 據某曾姓大神表示，看懂課本考古還是只會寫一點點
>> 然後還是考了90分
>>> 為什麼莫名其妙被賣了- -

## Murmur
> 大家都在線上呢~~是明天有甚麼大事嗎?
>> 可能是期中考ㄅ @@