Cryptography and computer security - Tutorial 27.10.2020

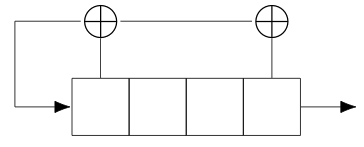
--- tags: vaje, kirv, lfsr, shannon hackmd: https://hackmd.io/GWYe1z9cQKmIrnD7WsjjLQ plugins: mathjax --- # Cryptography and computer security - Tutorial 27.10.2020 --- ## Linear feedback shift registers (LFSR) Example: ![Example LFSR](https://jaanos.github.io/kirv/notes/2020-21/2020-10-27/LFSR.png) * $z_{i+4} = z_{i+3} + z_i$ * $z_{i+n} = \sum_{j=0}^{n-1} c_j z_{i+j}$ * $0 = -z_{i+n} + \sum_{j=0}^{n-1} c_j z_{i+j}$ * $C(x) = -1 + \sum_{j}^{n-1} c_j x^{n-j}$ connection polynomial ### Exercise 1 Check that the polynomial $C(x) = 1 + x + x^4$ is irreducible over $\mathbb{Z}_2$. Is it also primitive over $\mathbb{F}_{2^4}$? ---- $C(x) = A(x) B(x)$ * irreducible polynomials of degree $1$ over $\mathbb{Z}_2$: $x$, $x+1$ * irreducible polynomials of degree $2$ over $\mathbb{Z}_2$: $x^2 + x + 1$ ``` (x^4 + x + 1) / (x^2 + x + 1) = x^2 + x - (x^4 + x^3 + x^2) x^3 + x^2 + x + 1 - (x^3 + x^2 + x) 1 ``` Hence, $C(x)$ is **irreducible** over $\mathbb{Z}_2$. * $2^4 - 1 = 15 = 5 \cdot 3$ non-zero elements of $\mathbb{F}_{2^4}$. * $C(x)$ is **primitive** over $\mathbb{F}_q$ if the lowest $t$ such that $C(x)$ divides $x^t - 1$ equals $q^d - 1$, where $d$ is the degree of $C(x)$. ``` (x^5 + 1) / (x^4 + x + 1) = x - (x^5 + x^2 + x) x^2 + x + 1 (x^15 + 1) / (x^4 + x + 1) = ... ``` $C(x)$ is **primitive** over $\mathbb{F}_{2^4}$. --- ### Exercise 2 Generate output sequences for an LFSR of degree $4$ with connection polynomial $C(x)$ and all possible initial states. What are their periods? ---- ``` 0|0|0|0|0|0|0|0|0|... period 1 000111101011001|0001 period 15 ``` --- ### Exercise 3 Determine all possible periods of LFSRs defined by the equations 1. $s_{i+3} = (s_i + s_{i+1} + s_{i+2}) \bmod{2}$, 2. $s_{i+4} = (s_i + s_{i+1} + s_{i+2} + s_{i+3}) \bmod{2}$, 3. $s_{i+4} = (s_i + s_{i+1} + s_{i+2} + s_{i+3}) \bmod{5}$, 4. $s_{i+4} = (s_i + s_{i+1} + s_{i+2} + s_{i+3}) \bmod{10}$. ---- 1. ``` 0|000 period 1 0011|001 period 4 01|010 period 2 1|111 period 1 ``` $C_1(x) \equiv 1 + x + x^2 + x^3 \equiv (1 + x) (1 + x^2) \equiv (1 + x)^3 \pmod{2}$ 2. ``` 0|0000 period 1 00011|0001 period 5 00101|0010 period 5 01111|0111 period 5 ``` $C_2(x) \equiv 1 + x + x^2 + x^3 + x^4 \pmod{2}$ ``` (x^5 + 1) / (x^4 + x^3 + x^2 + x + 1) = x + 1 - (x^5 + x^4 + x^3 + x^2 + x) x^4 + x^3 + x^2 + x + 1 - (x^4 + x^3 + x^2 + x + 1) 0 ``` $C_2(x)$ is **not primitive** over $\mathbb{F}_{2^4}$. --- ### Exercise 4 Determine whether an LFSR of degree $4$ can generate sequences 1. $1011010000101\dots$ and 2. $(011101110)^*$. --- ### Exercise 5 Find an LFSR of degree $4$ that generates the sequence $10101100$. --- ## Shannon theory ### Exercise 6 Prove that a cryptosystem has perfect secrecy if and only if $$ P(Y = y \mid X = x_1) \ = \ P(Y = y \mid X = x_2) $$ for all $x_1, x_2 \in \mathcal{P}$ and $y \in \mathcal{C}$. --- ### Exercise 7 Consider a cryptosystem in which $\mathcal{P} = \lbrace a, b \rbrace$, $\mathcal{K} = \lbrace k_1, k_2, k_3 \rbrace$ and $\mathcal{C} = \lbrace 1, 2, 3 \rbrace$. Suppose that keys are chosen with probabilities $P(K = k_1) = 1/2$, $P(K = k_2) = P(K = k_3) = 1/4$, and plaintexts are chosen with probabilities $P(X = a) = 1/4$, $P(X = b) = 3/4$. The encryption matrix is as follows: | $E_k$ | $a$ | $b$ | | ------------ | ---------- | ---------- | | $k_1$ | 1 | 2 | | $k_2$ | 2 | 3 | | $k_3$ | 3 | 1 | 1. Compute the probability measures on the ciphertext, i.e., $P(Y = y)$ for all $y \in \mathcal{C}$. 2. Prove that this cryptosystem does not provide perfect secrecy. 3. Modify the plaintext and/or key distributions in such a way that perfect secrecy is obtained. --- ### Exercise 8 Prove that the affine cipher over $\mathbb{Z}_{26}$ achieves perfect secrecy if every key is used with equal probability $1/312$.

Syntax	Example	Reference
# Header	Header	基本排版
- Unordered List	Unordered List
1. Ordered List	Ordered List
- [ ] Todo List	Todo List
> Blockquote	Blockquote
Bold font	Bold font
Italics font	Italics font
~~Strikethrough~~	~~Strikethrough~~
19^th^	19^th
H~2~O	H₂O
++Inserted text++	Inserted text
==Marked text==	Marked text
[link text](https:// "title")	Link
![image alt](https:// "title")	Image
`Code`	`Code`	在筆記中貼入程式碼
```javascript var i = 0; ```	`var i = 0;`
:smile:		Emoji list
{%youtube youtube_id %}	Externals
$L^aT_eX$	L^aT_eX
:::info This is a alert area. :::	This is a alert area.