2016q3 Homework1 (compute-pi)

# 2016q3 Homework1 (compute-pi) contributed by <`shelly4132`> ## Reviewed by <`hugikun999`> * 可以嘗試分析對數圖為何N越大時浮動越大。 * thread數對openmp有滿大的影響，可以多測試幾組找出造成差異的原因。 * AVX+unroll版本可以從function本身去修正，使其就算不為16的倍數時圖也不會出現明顯震盪。 * 分析為何Euler相對其它公式會上升如此快速。 * 信賴區間可以多做幾種取樣次數，比較不同取樣次數對曲線產生的影響。 ## 開發環境 * 作業系統：Ubuntu 16.04 LTS * CPU：Intel(R) Core(TM) i5-4200U CPU @ 1.60GHz * Cache： * L1d cache: 32K * L1i cache: 32K * L2 cache: 256K * L3 cache: 3072K >> 需要一併列出硬體組態，特別是 processor model，這樣才有比較分析的依據 [name=jserv] ## 總之先執行看看先從github上clone程式碼下來 ```shell $ git clone https://github.com/sysprog21/compute-pi ``` #### Makefile 打開Makefile可以看到已經預設打開OpenMP和AVX了 ```shell CFLAGS = -O0 -std=gnu99 -Wall -fopenmp -mavx ``` #### 開始執行 ```shell $ make check N = 400000000 , pi = 3.141593 4.47user 0.00system 0:04.47elapsed 99%CPU (0avgtext+0avgdata 1756maxresident)k 0inputs+0outputs (0major+85minor)pagefaults 0swaps time ./time_test_openmp_2 N = 400000000 , pi = 3.141593 5.65user 0.00system 0:02.83elapsed 199%CPU (0avgtext+0avgdata 1936maxresident)k 0inputs+0outputs (0major+88minor)pagefaults 0swaps time ./time_test_openmp_4 N = 400000000 , pi = 3.141593 9.33user 0.00system 0:02.45elapsed 379%CPU (0avgtext+0avgdata 1956maxresident)k 0inputs+0outputs (0major+92minor)pagefaults 0swaps time ./time_test_avx N = 400000000 , pi = 3.141593 1.31user 0.00system 0:01.31elapsed 100%CPU (0avgtext+0avgdata 1756maxresident)k 0inputs+0outputs (0major+83minor)pagefaults 0swaps time ./time_test_avxunroll N = 400000000 , pi = 3.141593 1.22user 0.00system 0:01.23elapsed 99%CPU (0avgtext+0avgdata 1772maxresident)k 0inputs+0outputs (0major+84minor)pagefaults 0swaps ``` 使用clock_gettime() 來測量不同實做的執行時間，需要花一點時間等待。 ``` $ make gencsv ``` 完成後可以發現資料夾裡多了一個csv檔 ``` result_clock_gettime.csv ``` 利用LibreOffice圖表 ![](https://i.imgur.com/uAJOFD8.png) 用gnuplot畫的結果 * set logscale x 2：設定x為以2為底的對數刻度 ![](https://i.imgur.com/FHaSwOu.png) 將N的大小提高 * 因為後面的時間差異比較大，所以我把logscale的底數改為10，然後x軸從5000開始 ![](https://i.imgur.com/zMXPfrd.png) ## 時間處理與 time 函式使用使用``` time ```指令可以看到以下三種時間 #### Real time：表示程式從執行開始到結束所花費的時間。 #### User time：表示這個程式運行在User mode的CPU time。 #### System time：表示這個程式運行在Kernel mode的CPU time。 #### Real time ≠ CPU time CPU time是指實際上CPU有在運作的時間，像等待使用者輸入的時間並不會被計算進去，但Real time會把那些時間都計算進去。而在多執行緒的情況下，CPU time是所有執行緒的總和。 #### 關於Kernel mode與 User mode 1. 之所以要有 Kernel mode 和 User mode 之分，是因為我們希望作業系統可以壟斷所有的硬體操作，讓一般的程式不能亂搞。 2. Kernel mode 就是萬能的，只要是 CPU 能管的硬體，Kernel mode 的程式就可以透過 machine code 來操作該硬體。 3. User mode 基本上就是「受限」的模式。除了一些沒有傷害的行為之外什麼都不能做。 ### clock_gettime() #### 函式原型 ```clike int clock_gettime(clockid_t clk_id, struct timespec *tp); ``` 第一個參數clk_id可填入： CLOCK_REALTIME：系統時間，會被NTP調整 CLOCK_MONOTONIC：時間自系統開機後就一直單調的遞增，但會被NTP調整時間，所以並不能算是絕對的單調遞增。 CLOCK_MONOTONIC_RAW：與CLOCK_MONOTONIC很像，只是他不會受到NTP的影響 CLOCK_PROCESS_CPUTIME_ID CLOCK_THREAD_CPUTIME_ID CLOCK_REALTIME_COARSE CLOCK_MONOTONIC_COARSE CLOCK_BOOTTIME CLOCK_REALTIME_ALARM CLOCK_SGI_CYCLE CLOCK_TAI 而struct timespec* tp則是本函式回傳的結果。 struct timespec的宣告如下： ```clike struct timespec { time_t tv_sec; /* seconds */ long tv_nsec; /* nanoseconds */ }; ``` ## baseline 利用此公式求得pi的值![](https://i.imgur.com/u16CAcL.png) ```clike= double compute_pi_baseline(size_t N) { double pi = 0.0; double dt = 1.0 / N; // dt = (b-a)/N, b = 1, a = 0 for (size_t i = 0; i < N; i++) { double x = (double) i / N; // x = ti = a+(b-a)*i/N = i/N pi += dt / (1.0 + x * x); // integrate 1/(1+x^2), i = 0....N } return pi * 4.0; } ``` ## OpenMP 用一樣的公式只是使用了OpenMp去做優化，function新增了一個參數(threads)用來指定要用幾個thread來執行 #### reduction * 他的形式為reduction( 運算元 : 變數 ) * 支援的運算元有 +, *, –, &, ^, |, &&, || * 變數則必須要是 shared 的他的運作方式，就是讓各個執行緒針對指定的變數擁有一份有起始值的複本（起始值是運算元而定，像 +, – 的話就是 0，* 就是 1），然後在平行化的計算時，都以各自的複本做運算，等到最後再以指定的運算元，將各執行緒的複本整合。 ```clike= double compute_pi_openmp(size_t N, int threads) { double pi = 0.0; double dt = 1.0 / N; double x; #pragma omp parallel num_threads(threads) { #pragma omp for private(x) reduction(+:pi) for (size_t i = 0; i < N; i++) { x = (double) i / N; pi += dt / (1.0 + x * x); } } return pi * 4.0; } ``` ## AVX SIMD AVX (Advanced Vector Extensions) 是 Intel 一套用來作 Single Instruction Multiple Data 的指令集。 * _mm256d : 它並不是一種暫存器，是指可以用來載入到 AVX 暫存器的 “Data type”，double precision, 64bit * _mm256_set1_pd(1.0)：將參數浮點數值放到 _mm256 變數的所有位置。 * _mm256_set_pd(dt * 3, dt * 2, dt * 1, 0.0)：將dt * 3, dt * 2, dt * 1, 0.0這些參數依序放入_mm256 變數，參數順序和放進去的次序相反。 ```C= double compute_pi_avx(size_t N) { double pi = 0.0; double dt = 1.0 / N; register __m256d ymm0, ymm1, ymm2, ymm3, ymm4; ymm0 = _mm256_set1_pd(1.0); ymm1 = _mm256_set1_pd(dt); ymm2 = _mm256_set_pd(dt * 3, dt * 2, dt * 1, 0.0); ymm4 = _mm256_setzero_pd(); // sum of pi for (int i = 0; i <= N - 4; i += 4) { ymm3 = _mm256_set1_pd(i * dt); // i*dt, i*dt, i*dt, i*dt ymm3 = _mm256_add_pd(ymm3, ymm2); // x = i*dt+3*dt, i*dt+2*dt, i*dt+dt, i*dt+0.0 ymm3 = _mm256_mul_pd(ymm3, ymm3); // x^2 = (i*dt+3*dt)^2, (i*dt+2*dt)^2, ... ymm3 = _mm256_add_pd(ymm0, ymm3); // 1+x^2 = 1+(i*dt+3*dt)^2, 1+(i*dt+2*dt)^2, ... ymm3 = _mm256_div_pd(ymm1, ymm3); // dt/(1+x^2) ymm4 = _mm256_add_pd(ymm4, ymm3); // pi += dt/(1+x^2) } double tmp[4] __attribute__((aligned(32))); _mm256_store_pd(tmp, ymm4); // move packed float64 values to 256-bit aligned memory location pi += tmp[0] + tmp[1] + tmp[2] + tmp[3]; return pi * 4.0; } ``` ## Error Rate ```clike= // Baseline double pi = compute_pi_baseline(N); double diff = pi - M_PI > 0 ? pi - M_PI : M_PI - pi; double error = diff / M_PI; ``` 之前測出來的error rate只有一條曲線，原本還覺得滿合理的，結果後來發現code有寫錯，改好後竟然多了一條曲線 orz ![](https://i.imgur.com/EuzO8om.png) 後來跟[鄭皓澤](https://hackmd.io/s/ryHY0T_T)討論後，發現是AVX Unroll在N = 1000結尾的時候pi的值都會跟別人不一樣，但為什麼會這樣的原因還有待進一步的研究。 >> 表示程式碼的實做可能有缺陷，想辦法去修正 [name=jserv] ``` time ./time_test_baseline N = 1000 , pi = 3.142592 0.00user 0.00system 0:00.00elapsed ?%CPU (0avgtext+0avgdata 1716maxresident)k 0inputs+0outputs (0major+83minor)pagefaults 0swaps time ./time_test_openmp_2 N = 1000 , pi = 3.142592 0.00user 0.00system 0:00.00elapsed ?%CPU (0avgtext+0avgdata 1788maxresident)k 0inputs+0outputs (0major+87minor)pagefaults 0swaps time ./time_test_openmp_4 N = 1000 , pi = 3.142592 0.00user 0.00system 0:00.00elapsed 200%CPU (0avgtext+0avgdata 1740maxresident)k 0inputs+0outputs (0major+93minor)pagefaults 0swaps time ./time_test_avx N = 1000 , pi = 3.142592 0.00user 0.00system 0:00.00elapsed ?%CPU (0avgtext+0avgdata 1788maxresident)k 0inputs+0outputs (0major+87minor)pagefaults 0swaps time ./time_test_avxunroll N = 1000 , pi = 3.126520 0.00user 0.00system 0:00.00elapsed ?%CPU (0avgtext+0avgdata 1792maxresident)k 0inputs+0outputs (0major+84minor)pagefaults 0swaps ``` ### 原因從以下程式碼可以看到它比Baseline多執行了16遍，當N=1000的時候，i最大可以到984，但984/16 = 61.5，不能整除，所以變成有漏算的情形。 ```clike= for (int i = 0; i <= N - 16; i += 16) { ymm14 = _mm256_set1_pd(i * dt); ymm10 = _mm256_add_pd(ymm14, ymm2); // x = i*dt+3*dt, i*dt+2*dt, i*dt+1*dt, i*dt+0.0 ymm11 = _mm256_add_pd(ymm14, ymm3); // x = i*dt+7*dt, i*dt+6*dt, i*dt+5*dt, i*dt+4*dt ymm12 = _mm256_add_pd(ymm14, ymm4); // x = i*dt+11*dt, i*dt+10*dt, i*dt+9*dt, i*dt+8*dt ymm13 = _mm256_add_pd(ymm14, ymm5); // x = i*dt+15*dt, i*dt+14*dt, i*dt+13*dt, i*dt+12*dt ymm10 = _mm256_mul_pd(ymm10, ymm10); // x^2 = i*dt+3*dt)^2, (i*dt+2*dt)^2, ... ymm11 = _mm256_mul_pd(ymm11, ymm11); // x^2 ymm12 = _mm256_mul_pd(ymm12, ymm12); // x^2 ymm13 = _mm256_mul_pd(ymm13, ymm13); // x^2 ymm10 = _mm256_add_pd(ymm0, ymm10); // 1+x^2 = 1+(i*dt+3*dt)^2, 1+(i*dt+2*dt)^2, ... ymm11 = _mm256_add_pd(ymm0, ymm11); // 1+x^2 ymm12 = _mm256_add_pd(ymm0, ymm12); // 1+x^2 ymm13 = _mm256_add_pd(ymm0, ymm13); // 1+x^2 ymm10 = _mm256_div_pd(ymm1, ymm10); // dt/(1+x^2) ymm11 = _mm256_div_pd(ymm1, ymm11); // dt/(1+x^2) ymm12 = _mm256_div_pd(ymm1, ymm12); // dt/(1+x^2) ymm13 = _mm256_div_pd(ymm1, ymm13); // dt/(1+x^2) ymm6 = _mm256_add_pd(ymm6, ymm10); // pi += dt/(1+x^2) ymm7 = _mm256_add_pd(ymm7, ymm11); // pi += dt/(1+x^2) ymm8 = _mm256_add_pd(ymm8, ymm12); // pi += dt/(1+x^2) ymm9 = _mm256_add_pd(ymm9, ymm13); // pi += dt/(1+x^2) } ``` ## 其他計算Pi的方式 ### Leibniz formula for π 考慮以下分解： ![image alt](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6358998bd99e608b5066ceda18a5211aae91472) 對兩邊從0到1去做積分 ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84dabc013f1b57c1d047303d68e28b3054c52e1) 當![](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fbcf3489c4ce0a4f161b2584ec1f31c70cbc5a6)時，除積分項以外的項收斂到萊布尼茨級數。同時，積分項收斂到0： ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/39b589297ef09eb07ad5c8acf06523fc4216ff45) 所以這便證明了萊布尼茨公式。 ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/8283f454140077256b47afadd702fed4b3b56569) ```clike= double compute_pi_leibniz(size_t N) { double pi = 0.0; int tmp = 1; for (size_t i =0; i < N; i++) { pi += tmp / (2.0 * (double)i + 1.0); tmp *= (-1); } pi *= 4; return pi; } ``` ## Euler ![](https://i.imgur.com/dOOXUpC.png) ```clike= double compute_pi_euler(size_t N) { double pi = 0.0; for (size_t i = 1; i <= N; i++) { pi += (1 / pow(i, 2.0)); } pi *= 6; return sqrt(pi); } ``` ![](https://i.imgur.com/m7AT6HX.png) ![](https://i.imgur.com/bYzgZIr.png) ## 信賴區間 **標準差：** 標準差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準差，代表大部分的數值和其平均值之間差異較大；一個較小的標準差，代表這些數值較接近平均值。而標準差定義為變異數的算術平方根。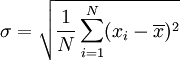 ![](http://wiki.mbalib.com/w/images/math/6/3/3/6336e4c48fd253b7a6f552fa2579525b.png) **標準誤差：** 標準誤差是指在抽樣試驗(或重覆的等精度測量)中，常用到樣本平均數的標準差。如果已知母體的標準差(σ)，那麼抽取無限多份大小為 n 的樣本，每個樣本各有一個平均值，所有這個大小的樣本之平均值的標準差可證明為 ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d743a1943f72e05a931abd58013ae5138dbb3b) 但由於通常σ為未知，此時可以用研究中取得樣本的標準差 (s) 來估計 ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/bef6d7a33e7d36b1d1734ef70e11c91f5f5ac13d)： ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/5dbfb77d27af35f8b95220e4ed06b6a12ae6b794) * 大於 95% 信賴區間 = ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/466e03e1c9533b4dab1b9949dad393883f385d80) + (s * 1.96) * 小於 95% 信賴區間 = ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/466e03e1c9533b4dab1b9949dad393883f385d80) - (s * 1.96) * ![](https://wikimedia.org/api/rest_v1/media/math/render/svg/466e03e1c9533b4dab1b9949dad393883f385d80)為樣本平均數 * s等於樣本平均數的標準差由上述公式算出信賴區間的最大與最小值 ```clike= double compute_ci(double *min, double *max, double data[SAMPLE_SIZE]) { double mean = 0.0; double stddev = 0.0; double stderror; int i = 0; //mean for(i = 0; i < SAMPLE_SIZE; i++){ mean += data[i]; } mean /= SAMPLE_SIZE; //standard deviation for(i = 0; i < SAMPLE_SIZE; i++){ stddev += (data[i] - mean) * (data[i] - mean); } stddev = sqrt(stddev / (double)SAMPLE_SIZE); //standard deviation stderror = stddev / sqrt((double)SAMPLE_SIZE); *min = mean - (1.96 * stderror); *max = mean + (1.96 * stderror); return mean; } ``` 用信賴區間篩選過數值的曲線圖 ![](https://i.imgur.com/pNQtpaw.png) ## 參考資料 * [簡介 Kernel Mode 與 User Mode 的概念](https://www.ptt.cc/bbs/b97902HW/M.1267018497.A.3B1.html) * [Linux 的 time 指令](http://yuanfarn.blogspot.tw/2012/08/linux-time.html) * [C語言：使用clock_gettime計算程式碼的時間需求](https://starforcefield.wordpress.com/2012/08/06/c%E8%AA%9E%E8%A8%80%EF%BC%9A%E4%BD%BF%E7%94%A8clock_gettime%E8%A8%88%E7%AE%97%E7%A8%8B%E5%BC%8F%E7%A2%BC%E7%9A%84%E6%99%82%E9%96%93%E9%9C%80%E6%B1%82/) * [Linux系统下的单调时间函数](http://m.blog.chinaunix.net/uid-20662820-id-3880162.html) * [廖健富學長](https://hackpad.com/Hw1-Extcompute_pi-geXUeYjdv1I) * [標準誤差-維基百科](https://zh.wikipedia.org/wiki/%E6%A0%87%E5%87%86%E8%AF%AF) * [許元杰的github](https://github.com/Jayjack0116/compute_pi)和[筆記](https://embedded2015.hackpad.com/-Ext1-Week-1-5rm31U3BOmh) * [簡易的程式平行化－OpenMP（五）變數的平行化](https://kheresy.wordpress.com/2006/09/22/%E7%B0%A1%E6%98%93%E7%9A%84%E7%A8%8B%E5%BC%8F%E5%B9%B3%E8%A1%8C%E5%8C%96%EF%BC%8Dopenmp%EF%BC%88%E4%BA%94%EF%BC%89-%E8%AE%8A%E6%95%B8%E7%9A%84%E5%B9%B3%E8%A1%8C%E5%8C%96/) * [詹志鴻學長的hackpad](https://embedded2015.hackpad.com/ep/pad/static/0aZx9N8YlMi) * [π的莱布尼茨公式](https://zh.wikipedia.org/wiki/%CE%A0%E7%9A%84%E8%8E%B1%E5%B8%83%E5%B0%BC%E8%8C%A8%E5%85%AC%E5%BC%8F)

Syntax	Example	Reference
# Header	Header	基本排版
- Unordered List	Unordered List
1. Ordered List	Ordered List
- [ ] Todo List	Todo List
> Blockquote	Blockquote
Bold font	Bold font
Italics font	Italics font
~~Strikethrough~~	~~Strikethrough~~
19^th^	19^th
H~2~O	H₂O
++Inserted text++	Inserted text
==Marked text==	Marked text
[link text](https:// "title")	Link
![image alt](https:// "title")	Image
`Code`	`Code`	在筆記中貼入程式碼
```javascript var i = 0; ```	`var i = 0;`
:smile:		Emoji list
{%youtube youtube_id %}	Externals
$L^aT_eX$	L^aT_eX
:::info This is a alert area. :::	This is a alert area.