# 2018q3 Homework1
contributed by <`yanjiunhaha`>
>這是固定格式,請注意
>[name=課程助教][color=red]
>>了解。[共筆示範](https://hackmd.io/s/Hyv1gVRux)所使用的格式好像不太一樣,所以讓我猶豫了。[name=YanJiun][time=Wed, Sep 19, 2018 12:33 AM]
> Homework2 之後才會嚴格要求格式 [name="jserv"]
---
## [2018q3 第 1 週測驗題](https://hackmd.io/s/S1a9-YO_Q#)
### Problem 1
::: success
嘗試不用 XOR 運算子做出等效的 XOR 運算。
:::
* 解答 :
```C
int my_xor(int x, int y) return (x | y) & (~ x | ~ y);
```
* 心得:
當我一看到這個題目,我馬上想到我在高中學到的數位邏輯。
$A \oplus B = \overline{A}B + A\overline{B}$
\begin{array}{|c|c|c|}
\hline
A \ B & 0 & 1 \\
\hline
0 & 0 & 1\\
\hline
1 & 1 & 0\\
\hline
\end{array}
但我看到 code 發現到它前面指定 `(x | y)`,我就思考了一下才想起它還有另一種表示法:
$A \oplus B = (A+B)(\overline{A}+\overline{B})$
* 延伸思考:
$\overline{A}B + A\overline{B}$ 與 $(A+B)(\overline{A}+\overline{B})$ 功能雖然一樣,但是用到的運算單元次數不一樣。
前者只用一次 Or,但有兩次 And。
`(~ x & y) | (x & ~ y)`
後者只用一次 And,但有兩次 Or。
`(x | y) & (~ x | ~ y)`
* And 和 Or 運算哪個比較快?
==我的猜想:~~And 比較快~~== ==一樣==
>仔細思考後,這些運算在一個系統中應該都已經整合成一個 ALU 了。
>即使這些運算真的有些微的延遲差異,其實應該都在系統整合時,就已經被**管線化**( Pipeline )。
>因此我們在考慮這類的效率問題,應該是要以==指令==層級來考慮。
>應該考慮程式碼所對應的==組合語言==,並且計算每個==指令==執行所需幾個 ==指令週期 ( Cycle )==。
>這裡 And 與 Or 的==指令週期==應該是一樣的。[name=YanJiun][time=Fri, Sep 21, 2018 10:16 AM][color=#0000ff]
:::warning
避免只用圖表去判斷特定 logic gate 是否「快」(這不是精準詞彙),請複習數位邏輯電路,用 pre-determined latency 來分析。
:notes: jserv
:::
這是一張 4 bits 加法器,可以做一般的加/減法 ($S$ 可以控制),由四個半加器 (FA) 構成。
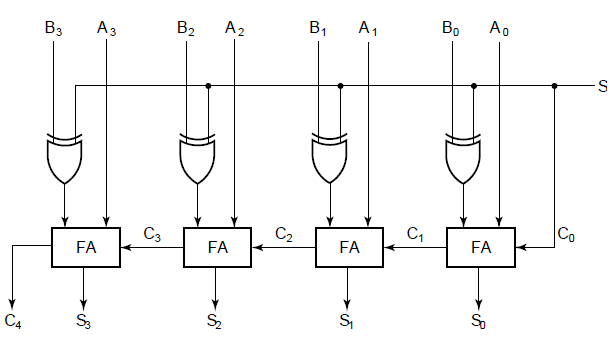
###### [image resource](https://www.chegg.com/homework-help/questions-and-answers/want-make-4-bit-ripple-carry-adder-subtractor-using-verilog-hdl-made-4-bit-ripple-carry-ad-q13057505)
根據上圖,如果我們想要讓這個加法器也可以做出邏輯運算的效果,我們只須改動一小部份。
* And 運算:
將每一級的 $C_i$ 不要接上下一級的 FA ,且直接將 $C_i$ 輸出及是 $A_i\&B_i$($S$ 為 $0$)。
* Or 運算:
將每一級的 $C_i$ 不要接上下一級的 FA ,且將 $C_i$ 與 $S_i$ 做 Or 運算後輸出及是 $A_i|B_i$
($S$ 為 $0$)。
Or 運算會多出一個 Gate 的延遲時間,因此做出此猜想。
但這也只是我目前所學,實際上電腦的 CPU 設計可能不是如此簡單。
---
### Problem 2
:::success
Parity (check) bit 可翻譯為「奇偶校驗位元」或「同位檢查位元」。
:::
* 解答
```C
int max = 16;
while (max >= 8) {
num = num ^ (num >> max);
max /= 2;
}
```
由於後面這行`return table[num & 0xff];`,這裡的 table's size 只有 $256$。
需要將 num 降到 $256$ 以下。
但我關注的重點不是 `max` 應該`/=`多少,而是這裡使用的 `^`。
(Xor 的真值表可以往上找)
根據 Xor 的特性我們可以發現,`1` 將會兩兩消除,因此不會影響奇偶校正結果。
:::info
example
1101_0011 $\Rightarrow$ 1101 ^ 0011 $\Rightarrow$ 1110
0011_1011 $\Rightarrow$ 0011 ^ 1011 $\Rightarrow$ 1000
:::
* 心得
我一眼先看到這段程式碼
```cpp
/* Generate look-up table while pre-processing */
#define P2(n) n, n ^ 1, n ^ 1, n
#define P4(n) P2(n), P2(n ^ 1), P2(n ^ 1), P2(n)
#define P6(n) P4(n), P4(n ^ 1), P4(n ^ 1), P4(n)
#define LOOK_UP P6(0), P6(1), P6(1), P6(0)
```
冷靜分析一下馬上就懂了。
1. `n ^ 1` 其實等效於 `!n`
2. `LOOK_UP ` 列出前幾項
```
0110_1001_1001_0110
1001_0110_0110_1001
1001_0110_0110_1001
0110_1001_1001_0110
```
0~10~ = 000~2~ $\Rightarrow$ 0
1~10~ = 001~2~ $\Rightarrow$ 1
2~10~ = 010~2~ $\Rightarrow$ 1
3~10~ = 011~2~ $\Rightarrow$ 0
不知道你看出規律了沒,我多列了幾行。
3. `unsigned int table[256] = { LOOK_UP };`
事實上這個 `table` 是一個 $16\times16$ 的**對稱矩陣**。
當下我馬上想要縮減這個矩陣,以減少佔用記憶體空間。
很快的,我便覺得這個`table`可以直接使用**演算法**替代。
* 缺點是這樣的程式將無法確定在==常數時間==完成。
* 優點是可以省下`256*sizeof(int)`的記憶體空間。
* 延伸思考
那可以用哪些**演算法**取代呢?
1. 計算資料裡`1`的個數
```C
int count = 0;
while(n) {
n = n & (n-1);
++count;
}
return count & 0x1;
```
這個算法的複雜度是`n`有幾個`1`就跑幾次。
2. 使用上面程式碼的概念
```C
while (max) {
n = n ^ (n >> max);
max >>= 1;
}
return n & 0x1;
```
這個演算法的時間複雜度則取決於輸入資料寬度,$log_2(sizeof(n))$。
3. [week3 隨堂測驗-3](https://hackmd.io/s/BkyQskjK7#)
```c
#include <stdint.h>
int parity(uint32_t x)
x ^= x >> 1;
x ^= x >> 2;
x = (x & 0x11111111U) * 0x11111111U;
return (x >> 28) & 1;
}
```
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet