---
breaks: false
---

We thank the reviewers for their valuable and insightful comments.

## General Comments

### Single Precision (Rev 2, 3)

> Rev 2: The comment on the precision limitation is very worrying.

> Rev 3: the work only considers single precision (as mentioned in the Limitations) due the RT cores limitations

We acknowledge that single precision is an inherent limitation of the RT cores and discuss the consequences to our experiments in Sec. VI-C.
In practice, every particular simulation task will have a specific demand for precision and can opt for other, slower implementations of Barnes-Hut algorithm if single precision is not enough for its purposes.

On a more general note, recall that early GPGPU programmers faced the same issue with traditional shader cores, and it was eventually addressed by the manufacturer. We believe that works like ours highlight the general applicability of RT cores and provide a compelling reason for the similar action. If double precision support is added to RT cores, RT-BarnesHut will require minimal modifications to run.

### End-to-end times, exclusion of tree-build and sort times (Rev 2, 4)

> Rev 2 : For Table 1 you mention that you do not show the tree-build and sort times, but for completeness could you also provide a plot/table that includes those?

> Rev 4: Evaluation doesn't provide full picture of the overhead distribution at runtime (i.e., excluded tree-build and sort time). Thus, no data is provided to justify the speedup to overall runtime.

We did not include the tree build and sort times as our contribution is the accelerated force computation kernel -- a separate phase of the computation.
In particular, the user can provide a pre-built tree and RT-BarnesHut will be able to do its job just as well.
As the tree build and sort times are common to both RT-BarnesHut and ChaNGa,
they don't add anything meaningful to the comparison, in our view. But we have these numbers and can include them in the paper for completeness.

### Utilization and peak performance of RT cores (Rev 1, 4)

> Rev 1: What are the necessary modifications to be made to reach good performance on RT hardware? Add pseudocode about that?

> Rev 1: What is the peak (hardware) performance that it is possible to get? For instance, 200x speedup does not mean that it is a good performance if you get only 10% of the performance that you could get.

> Rev 4: Evaluation doesn't go deep into the computation efficiency level study (i.e., how well the implementation utilizes the computation power provided by RT cores).As from the computation efficiency perspective, reviewer is unclear how efficiently the implementation runs over the RT cores, e.g., if it doesn't leverage the same level of efficiency compared to the original RT algorithms.

NVIDIA's RT hardware internals is proprietary information. We only know that it accelerates Bounding Volume Hierarchy traversal and ray-triangle intersection tests.

As we mention in Sec.VI-C, although RT cores profiling was added to the Nsight Graphics (Pro build) profiler, it can only profile rendering of images.
We cannot use the profiler since RT-BarnesHut only computes and does not render anything.
Besides, the Nsight Compute profiler does not support RT cores.

### Scalabilty (Rev 2, 3)

> Rev 2: there is limited result presented with respect to scalability

> Rev 3: What is the scalability of the algorithm with respect to number of processes, or number of threads in a GPU?

[Inter-node situation]
General-purpose non-graphical computations on RT cores is an emerging field, of which RT-BarnesHut is a representative of. None of such applications, to our knowledge, has been used in multi-GPU setups. We leave investigation of this prospect to the future work.

[Intra-node situation]
The number of GPU threads used by RT-BarnesHut is equal to the number of bodies in the input, because we map each body in the dataset to a ray. Hence, it is not possible for us to vary this parameter.
Note that this doesn't limit the size of the input because the interface supports creation orders of magnitude more GPU threads than what we use. The GPU threads are green threads, which the hardware maps to RT cores.

### Hardware Setup (Rev 2, 5)

> Rev 1: You mention that you use 48 24-core AMD CPUs and that you have one RTX 4070. Is the GPU on a per-node basis? I.e., do you have 48 nodes with one GPU each?

> Rev 5: V-A mentions that the hardware used are 48 AMD CPUs. There is no mentioning distribution through MPI, or similar, and no graph contains CPU counts. Is it really 48 CPUs, or is this a typo, and it's rather one CPU? This would also fit to the one GPU.

Our setup consists of a single node with 48 24-core CPUs and one RTX 4070 GPU in total.
While RT-BarnesHut doesn't use multiprocessing on CPU, our baseline, ChaNGa, does.

## Proposed changes

* Add details on Optix and RT cores operation and our hardware setup (Rev 1, 2, 5) in exchange of making Section VI more concise (Rev 2, 5)

* Clarify the description of Algorithm 1 following the questions in Rev 3 and the formation and placement of triangles in the scene (Rev 5).

* Add a link to the implementation (Rev 5).

## Detailed Comments

### Rev 1

> What does the RT hardware look like? A diagram that illustrates that is very welcome.

Unfortunately, there is no publicly available information on what the hardware looks like. However, we know that the RT cores are present in each SM and share the same device memory as the other shader and tensor cores as shown in the figure below (taken from [Nvidia's blog][turing-arch]):


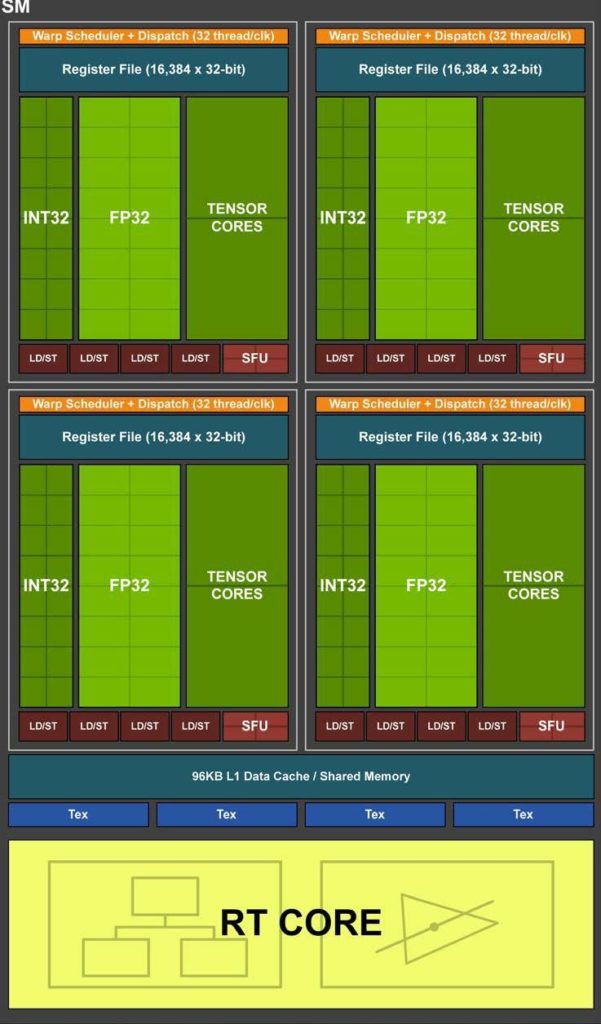
[turing-arch]: https://developer.nvidia.com/blog/nvidia-turing-architecture-in-depth/

### Rev 2

> While for n-body simulations the proposal appears to be new, it heavily
borrows ideas from a previous paper that used ray-tracing HW for database
queries, which makes the paper's contribution somewhat incremental.

The reduction proposed in prior work was restricted to a 1-d search space, where the reduction explicitly encodes that single dimension restriction. Though we used the basic idea of embedding a search space, we show that it can be generalized to a new space of problems.

### Rev 3

> What is the output of the algorithm?

For every body in the input dataset, we compute and output the force exerted by other bodies on it. The output maps every body to the force exerted on it by other bodies in the dataset.

> What is the computational complexity of the algorithm? Is it O(log N)?

The complexity is O(n log n), where n is the number of bodies.

> Could you describe what NodeSuccesor() do exactly?

It determines the next node to test for intersection, which is either the node's depth-first successor or the autorope-linked node.

> On line 12, the algorithm truncates the traversal and jump to the next node by setting the ray’s origin to the autorope location. What happens when we are in the leftmost triangle? (for example node H in Figure 4).

When building the tree, we mark the last node in depth-first order so that traversal terminates when we reach the last node. *Am I understanding the qn correctly?*

> The details of the NNS approach were not clear to me. Are the authors saying that an NNS approach as presented in [10] wouldn’t be an appropriate solution for the problem?

Correct: NNS falls in the same category of "N-body problems" (note the plural in "problems") but is distinct from the classical N-body problem that Barnes-Hut solves. Both of the problems are traditionally accelerated with tree-shaped data structures. Despite the similarity, the ray-tracing reduction of NNS can't be re-purposed for Barnes-Hut because the NNS reduction computes exclusively at the leaves of the tree. In contrast, we device a ray-tracing reduction of Barnes-Hut that computes at both leaves and internal nodes, and therefore, is more general than the NNS reduction and all other known to us ray-tracing reductions of general-purpose problems.

### Rev 4

> [RT-BarnesHut is] compared with a single baseline (ChaNGa)

ChaNGa is the current state-of-the-art GPU-based Barnes-Hut implementation. Our next best option was Treelogy [6], but we also wanted to base our evaluation on real-world data. We found that for real-wrold data, which is usually very skewed, the trees constructed by Treelogy do not fit in our GPU memory (12 GB). Unsurprising, as initially Treelogy was evaluated on synthetic datasets only.

Nevertheless, we performed preliminary experiments against Treelogy on synthetic datasets
and found RT-BarnesHut to be at least 2x faster in all cases.

> It would make the paper stronger (as for justifying a SC paper) if similar RT core utilization can be demonstrated via another n-body application.

> Reviewer appreciates the discussion on potential extension to other n-body problems. It would significantly help convince the proposed technique is generic if authors can also demonstrate via another n-body application.

Thank you for highlighting this part of our discussion.
Given the previous works (e.g. nearest-neighbor search on RT cores) and our work, we observe that every reduction to ray tracing is intimately connected to the problem at hand.
So we expect non-trivial changes have to be made to our reduction to re-purpose it to another n-body problem.
Our discussion only meant to say that such reductions to other problems in the class are possible.
Actually finding such reductions is beyond the scope of our work.

### Rev 5

> It does not look like RT-BarnesHut is available/open source software

It is available [on GitHub](https://github.com/vani-nag/OWLRayTracing/tree/BarnesHutRT/samples/cmdline/s04-rohan), and we are submitting an artifact.

>The bucket size of 32 and 64 is tested, but what about other values, also in between? That would allow showing setting the setup time and runtime (as a ratio) in relation to the bucket size, allowing to pick an optimal value

For ChaNGa, the state-of-the-art implementation of Barnes-Hut, an analysis around bucket sizes was done before [21], and we choose 32 and 64 to match their experiments.
The optimal values will be hardware- and dataset dependent, and reporting an optimum for our setup wouldn't help users of RT-BarnesHut with another setup.
But it would be easy to add more data points with varying bucket sizes and the analysis, if the reviewer deems it beneficial.

> Fig 3: Making an even clearer connection between text and figure would be good by incorporating more variables / quantities (like rho or epsilon); in the description (end of III-A), the triplet for the vertices of the triangles are not really explained. This part could be more elaborate!

We will elaborate on the formation and placement of triangles.

> Table II: The speed-up for the synthetic-25M case diminishes; why is this?

As Table II shows, the problem is input sensitive (not only input-size sensitive): synthetic datasets have a vastly different nature, and there doesn't seem to be a relation between their processing times and those of the real-world datasets (and there is no reason to believe there would be such relation).
In contrast, Fig. 5 (where synthetic-25M is one datapoint) allows to assess sensitivity to input sizes alone, controlling for the characteristics of the input values (all datasets have the same distribution). Fig. 5 shows that our advantage over ChaNGa grows with the size of the synthetic dataset.