:::section{.abstract}

Bitwise operators in Java are among those operators that perform their tasks at a binary level directly on binary digits (also known as bits), the smallest form of data in a computer or its data types. These bitwise operators are faster and an efficient way to interact with computers to make heavy computation in a linear time because they work directly with the bits rather than through a level of abstraction of software.

The image below shows the steps required to perform arithmetic operations on decimal and binary data.

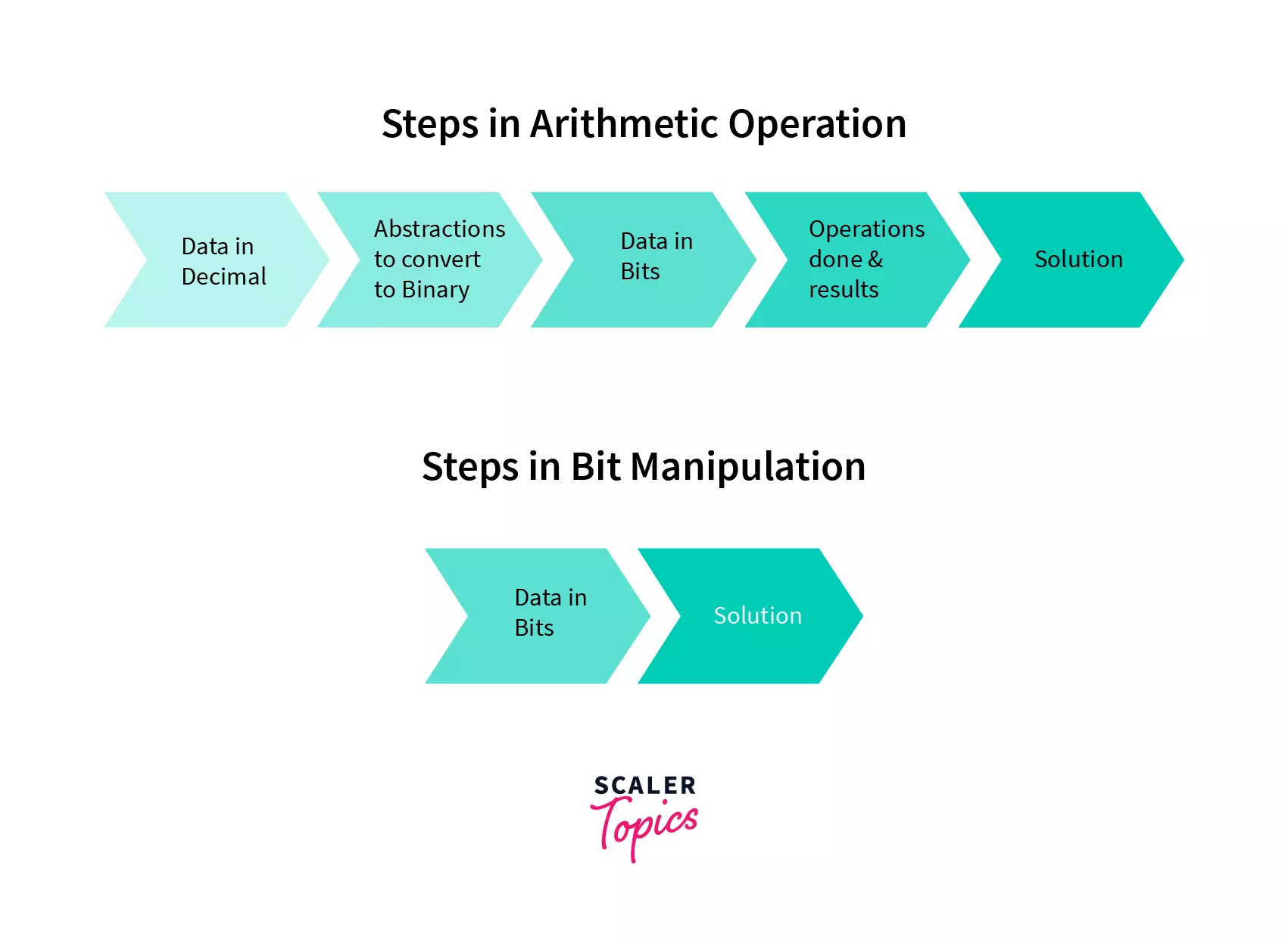
Bit Manipulation is performed using Bitwise Operators in Java on each bit of a number individually and can be used with any data type, such as int, float, short, char, etc.

Bitwise operators work internally on a binary equivalent of decimal numbers, i.e. the operation is performed on decimal numbers and internally, these operators work on individual bits bit by bit, as per the given operations:
The process begins by converting the operands into binary form. Then, the operator is executed on each binary number, producing the result. Finally, the resulting binary value is converted back into its decimal representation.
Standard arithmetic operators perform operations on human-readable values (3+4), while bitwise operators manipulate the low-level data directly.
:::

:::section{.main}

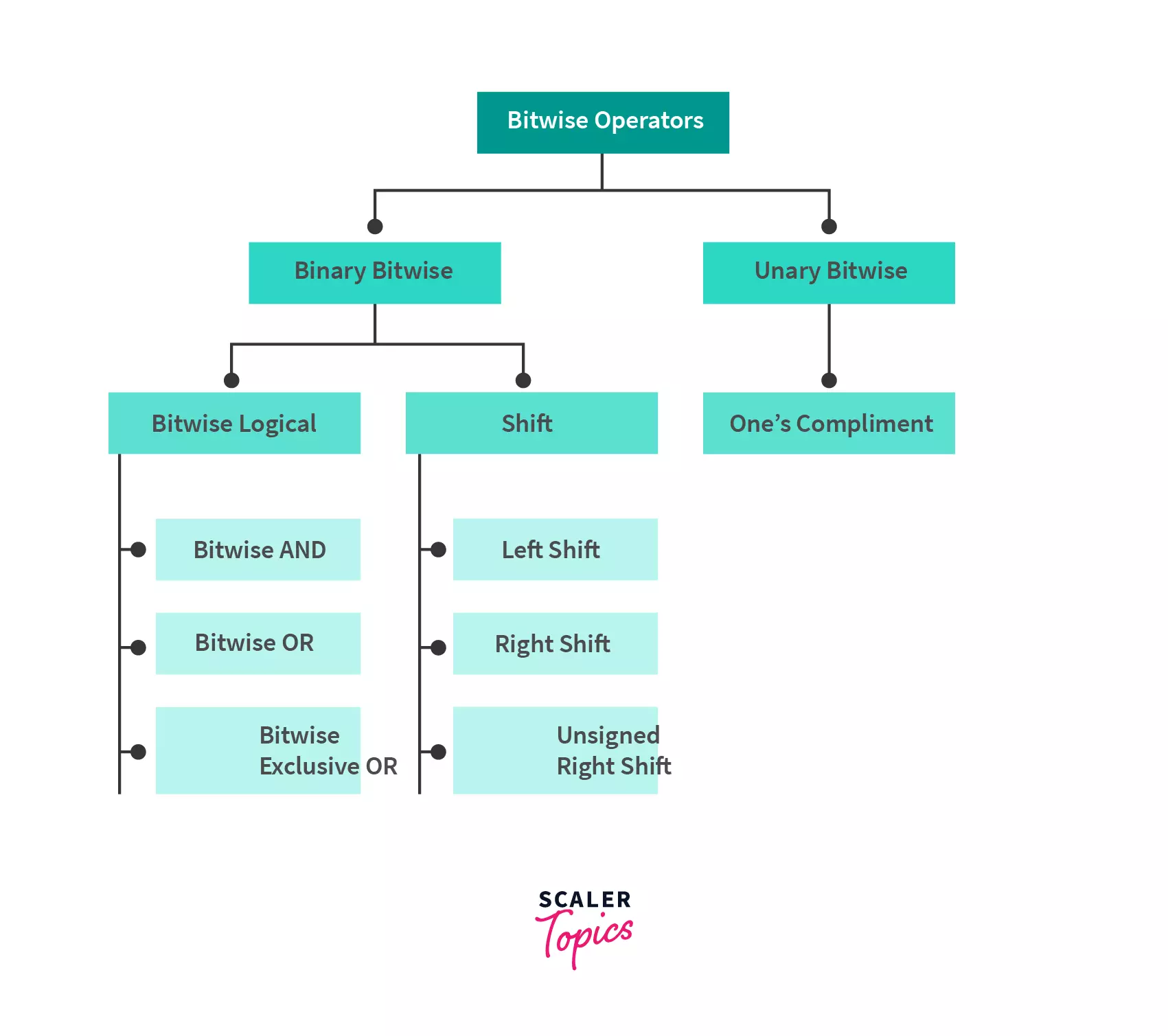
Types of Bitwise Operators in Java

There are six types of bitwise operator in Java:

1. Bitwise AND
2. Bitwise inclusive OR
3. Bit Shift Operators
4. Bitwise Compliment
5. Bitwise exclusive OR

Operators	Symbol	Uses
Bitwise AND	&	num1 & num2
Bitwise Exclusive OR (XOR)	^	num1 ^ num2
Bitwise Inclusive OR	|	num1 | num2
Bitwise Complement	~	~ num
Bitwise Left shift	<<	num1 << num2
Bitwise Right shift	>>	num1 >> num2
Unsigned Right Shift Operator	>>>	num1>>>num2

Let's go through all these operators one by one.
:::

:::section{.main}

Bitwise AND(&)

AND (&) is a important binary operator which compares two binary operands of equal bit length. For every bit, the operation checks if both bits are 1 across both operands. If true, bit will be set to 1 in the answer. Else, the resulting bit is set to 0.

Its Truth Table:

1 & 0 => gives 0
0 & 1 => gives 0
0 & 0 => gives 0
1 & 1 => gives 1

Example:

We want to perform Bitwise AND Operation of 6 and 8 (6 & 8), then.

​​​​    a = 6 = 0110 (In Binary)
​​​​    b = 8 = 1000 (In Binary)

​​​​      
​​​​      0110
​​​​    & 1000
​​​​     ________
​​​​      0000  = 0 (In decimal) 

:::

:::section{.main}

Bitwise OR(|)

The OR operaor is denoted by '|'. It perform bitwise (i.e bit by bit) or of input operands, if either of bits is 1 then it will give 1 otherwise it will give 0.

Its Truth Table:

1 | 0 => gives to 1
0 | 1 => gives to 1
1 | 1 => gives to 1
0 | 0 => gives to 0

Example:

We want to perform Bitwise OR Operation of 6 and 8 (6 | 8), then

​​​​    a = 6 = 0110 (In Binary)
​​​​    b = 8 = 1000 (In Binary)

​​​​   
​​​​      0110
​​​​    | 1000
​​​​     ________
​​​​      1110  = 14 (In decimal)

:::

:::section{.main}

Bitwise Complement (~)

The Bitwise Not means the negation of each bit of the input value. It takes only one integer. It is also called Complement operator.
All samples of 0 become 1, and all samples of 1 become 0. In other words, NOT invert each input bit. This inverted cycle is called the 1’s complement of a bit series.

This makes the number negative as any bit sequence starting with 1 is negative, as here N = ~N always produce results -(N+1). Because the system store data in the form of 2's complement which means it stores ~N like this.

~N = -(~(~N)+1) =-(N+1). 

Example:

We want to perform a Bitwise Complement of 6 (~6), then

1. Representing the number in binary format
   a = 6 => 0110 (In Binary)

2. Now we have to find ~6(means 1's compliment of 6)
   0000 0110 => 1111 1001 (flip each 1's to 0 and vice versa)
   So, ~6 = 1111 1001,
   Here, MSB(Most Significant Bit) is 1(means negative value).
   Then, in memory, it will be represented as 2's compliment
   (To find 2's compliment, we first have to find 1's compliment and then add 1 to it.)

3. Finding 2's compliment of ~6 i.e 1111 1001

                   1's compliment                Adding 1 to it
       1111 1001 ==================> 0000 0110 =================> 0000 0110
                                                                  +       1
                                                                  ---------
                                                                  0000 0111 
        So, 2's compliment of 1111 1001, is 0000 0111 

4. Converting back to decimal format.
   0000 0111 => 7

In step2: we have seen that the number is negative, so the final answer would be -7

​​​​   So, ~6 === -7 (result of bitwise complement)

:::

:::section{.main}

Bitwise XOR (^)

The bitwise XOR operation (^) is a binary operator that takes two input states and compares each corresponding bit. If the bits are opposite, the solution has a 1 in that bit position, and if they are matched, a 0 is returned.

1 ^ 1 => gives 0.
0 ^ 0 => gives 0.
1 ^ 0 => gives 1.
0 ^ 1 => gives 1.

Example:

We want to perform Bitwise XOR Operation of 6 and 8 (6 ^ 8), then.

​​​​    a = 6 = 0110 (In Binary)
​​​​    b = 8 = 1000 (In Binary)

​​​​      0110
​​​​    ^ 1000
​​​​     ________
​​​​      1110  = 14 (In decimal)

:::

:::section{.tip}

• XOR is used to flip selected single bits in a register or replace bit patterns that show Boolean states.
• It is widely used in cryptography and in producing parity bits to check error and fault tolerance.
  :::

:::section{.main}

Bit Shift (>>, <<,>>>)

A "bit shift" refers to a fundamental bitwise operation used to manipulate binary data efficiently in computing. It involves moving the positions of binary digits within a number's representation either to the left or right, based on a specified number of spaces indicated by the second operand. This operation can be applied to integral data types including integers (such as int, long, short), bytes, and characters (char).

There are four types of shifts:

1. Signed Left shift operator (<<)
2. Signed Right shift operator(>>)
3. Unsigned Left shift operator (<<<)
4. Unsigned Right shift operator (>>>)

a. Signed Left shift operator: << is the left shift operator and meets both logical and arithmetic shifts’ needs.

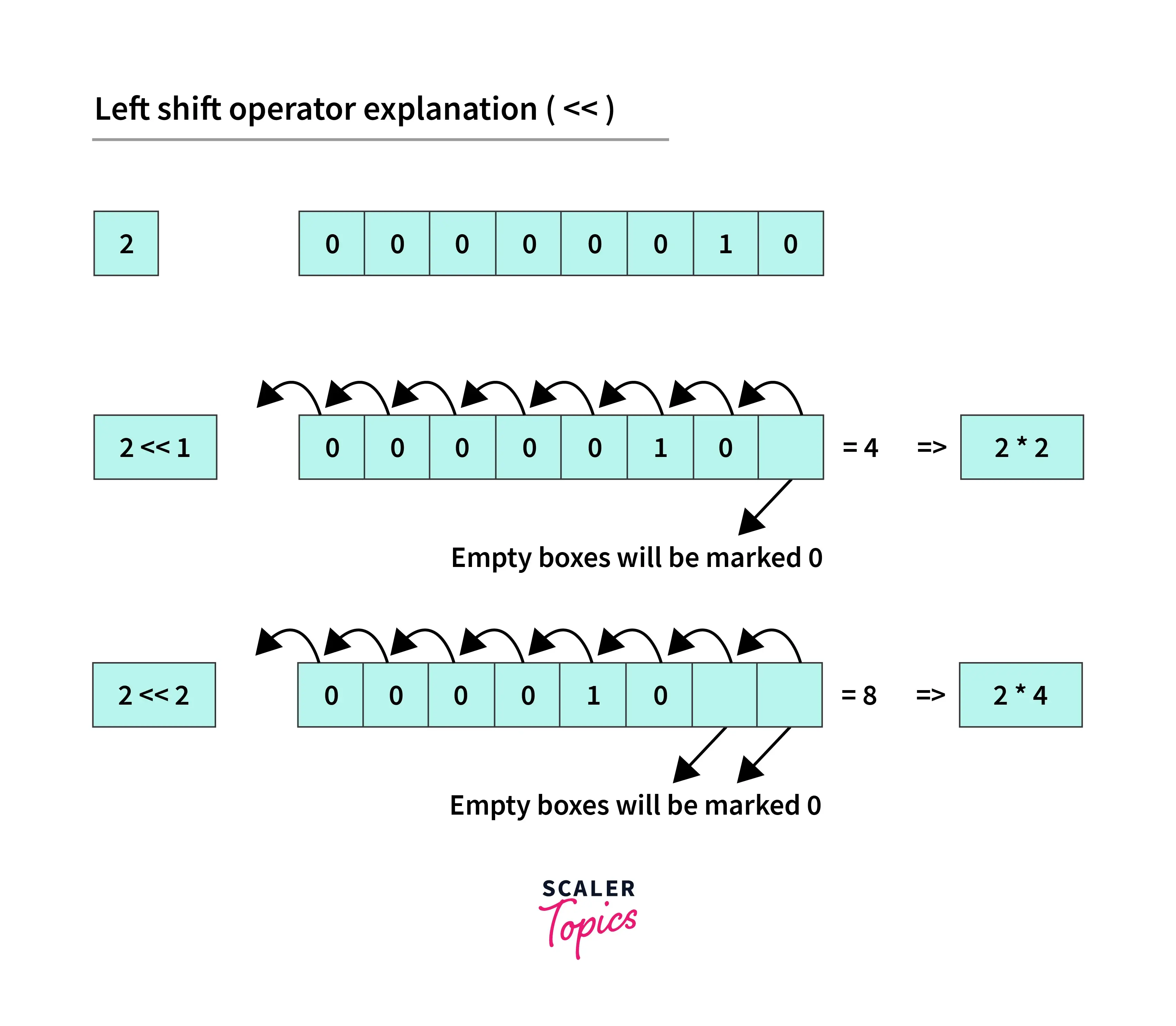
Example:

// left shift of 2
2 = 0010 (In Binary)

// perform 2 bit left shift
2 << 2: 0010 << 2 = 1000 (equivalent to 8)

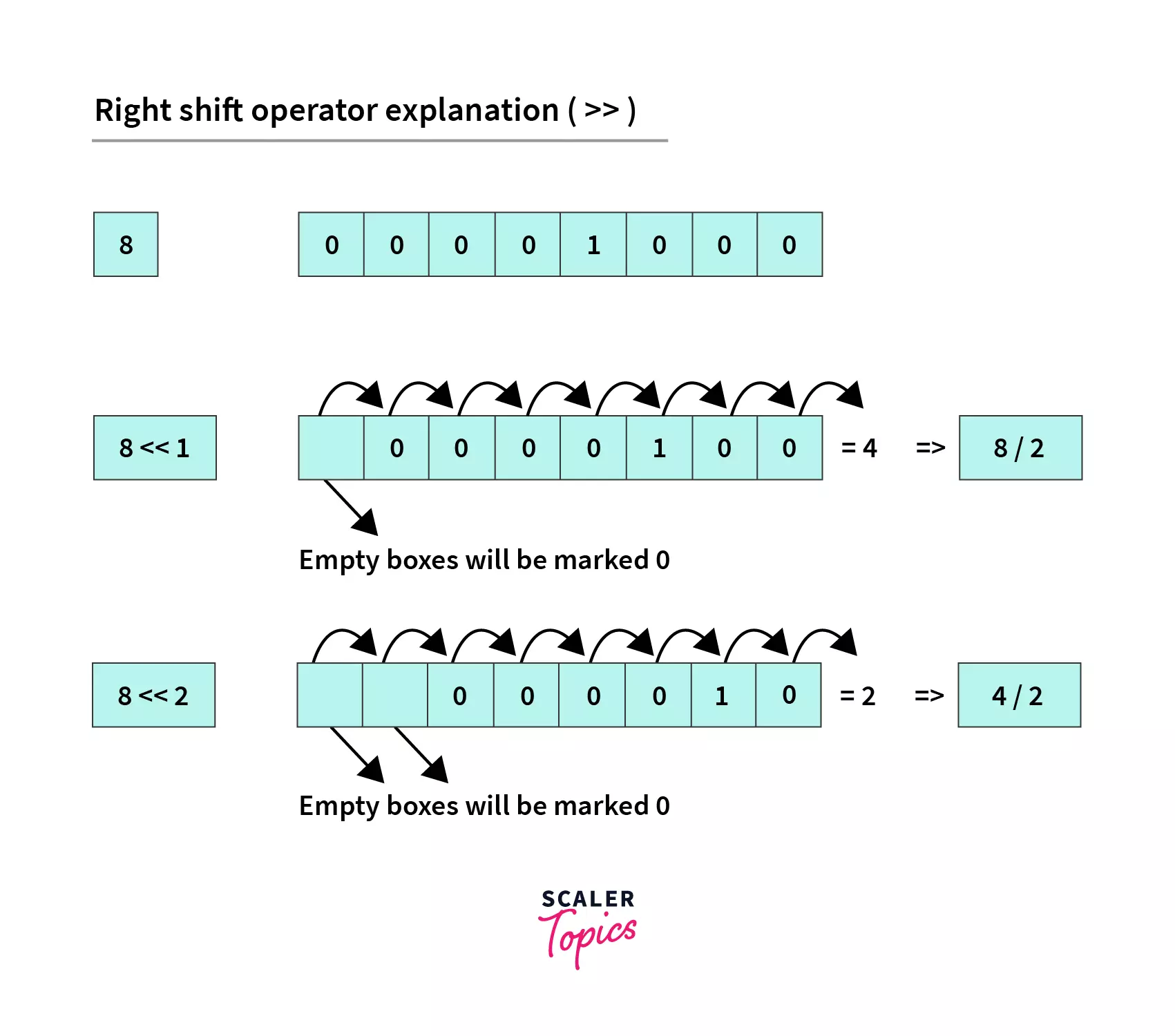
b. Arithmetic/signed right shift: >> is the arithmetic (or signed) right shift operator.

Example:

// right shift of 8
8 = 1000 (In Binary)

// perform 2 bit right shift
8 >> 2:
1000 >> 2 = 0010 (equivalent to 2)

c. Unsigned Left shift operator: <<< is the logical (or unsigned) left shift operator. It performs the same operation as the left shift operator, but its sign is not preserved.

d. Unsigned Right shift operator: >>> is the logical (or unsigned) right shift operator. It performs the same operation as the right shift operator, but its sign is not preserved in the operation.

Example:

// unsigned right shift of 8
8 = 0000 1000 (In Binary)
        
// Unsigned shift ``>>>`` will not keep the sign bit 
// (thus filling 0s) for positive numbers
        
8 >>> 2 = 0000 0010 ==> 2 (in decimal)

// unsigned right shift of ``-8``
// however, here numbers are not filled with zero as above
-8 = 1111 1000 (see calculation above)

-8 >>> 2 = 1111 1110 ==> 254 (in decimal)

:::

:::section{.main}

Advantages of Bitwise Operators in Java

1. You will have situations where you would like to set/clear/toggle just one specific bit of a register without operating on the whole register. Using bitwise operators in Java, you can do a read and perform an OR/AND/XOR operation with the suitable mask to modify only the desired bit position.
2. Usually, bitwise operations are faster than doing multiply/divide.
3. Similarly, if you wish to use an array as a circular queue, it'd be faster(and more elegant) to handle wraparound checks with bit-wise operations (your array size should be a power of 2).
4. Also, if you want a program error flag' to hold multiple error codes together for multiple scenarios, each bit can hold a separate value. You can ANDit with each error code as a check. One such use case isUnix error codes`.
5. Also, a n-bit bitmap can be a compact data structure. If you want to allocate a resource pool of size n, we can use n-bits to represent the current status.
6. In Compression & Encryption, both heavily depend on bitwise algorithms. For example, look at the deflate algorithm - everything is in bits, not bytes. For example:- Huffman Coding (for compression) and Data Encryption Standard (for encryption)

:::

:::section{.summary}

Conclusion

• Bitwise operators in Java are faster than standard arithmetic operators, which operate on decimal numbers.
  Logical and Bitwise operations are two different types of operations. The former operate on boolean data types, whereas the latter operate on bits.
• AND bitwise operator returns 1 if both bits are set.
• OR bitwise operator returns 1 if at least one of the operand bits is set.
• XOR bitwise operator returns 1 if the operand bits are opposite in value.

:::
:::section{.faqs}

FAQs

Q1. What are bitwise operators?
A: Bitwise operators in java are operators used to manipulate individual bits of binary numbers.

Q2. How many bitwise operators are there?
A: There are six bitwise operators in most programming languages: AND (&), OR (|), XOR (^), NOT (~), left shift (<<), and right shift (>>).

Q3. In which scenarios are bitwise operators commonly used?
A: Bitwise operators are commonly used in low-level programming, such as device drivers, embedded systems, cryptography, and optimization tasks.

Q4. Are bitwise operators platform-independent?
A: Yes, Bitwise operators themselves are generally platform-independent.
:::