---
title: 數學軟體實作 - Exam 3
tags: 2020 Fall - 數學軟體實作
GA: G-77TT93X4N1
---

# Exam 3

> 考試時間: 9:00-9:50AM

此份試卷滿分 100 分, **請任選兩題作答**, 各 50 分.

> 第 1, 2 題為上機, 需上傳 github.
> 第 3 題為手寫, 需繳交紙本答案卷.

> 請在 9:50AM 前上傳上機考題的的 m-file 至 github (Tuesday) 並 pull request.

> 可以任意使用 matlab 內建或個人 github repo 裡的所有程式及函數

---

## Problem 1 - 多邊形面積 (`github`)

若我們知道一個多邊形其每個角的位置, 逆時鐘方向依序為 $(x_1, y_1)$, $(x_2, y_2)$, $\cdots$, $(x_n, y_n)$, 則此多邊形面積為
$$
A = \frac{1}{2}\left[(x_1y_2 - x_2y_1) + (x_2y_3 - x_3y_2) + \cdots + (x_{n-1}y_n - x_ny_{n-1}) + (x_ny_1 - x_1y_n)\right].
$$
試寫一 `matlab` 程式, 利用以上公式算出給定多邊形面積.

> 此程式需讓使用者以滑鼠點選多邊形其角之位置

> 多邊形其角之個數為使用者決定

> 需說明清楚如何使用此程式

> 其 `output` 為多邊形面積

---

## Problem 2 - 動畫 (`github`)

載入一張照片後, 將照片長寬皆裁剪成$3$的倍數, 並將照片分成九宮格. 將右下角格子移除顯示為某一顏色. 接著作出以下動畫

> 只需針對特定圖片, 不需對所有圖片都適用

> 無 `input` 及 `output`, 只需顯示出動畫即可

{%youtube ap76X0W_o3M %}

---

## Problem 3 - 面積比例 (寫在紙上)

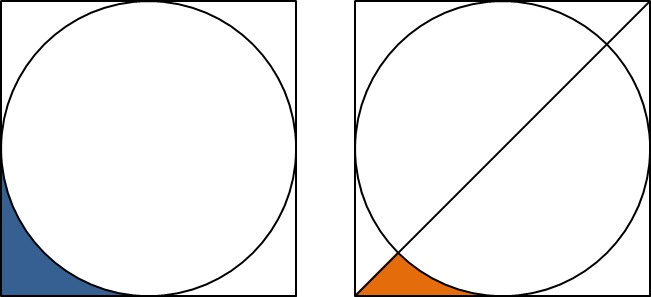
將一個半徑為 $1$ 的圓外接一個正方形. 我們將左下角圓的外面方形裡面的區域定義為一個藍色區域.

接著連接方形左下角及右上角可得一直線並將此藍色區域分為兩塊, 下方的那塊定義為橘色區域, 可知橘色區域面積為藍色的一半.


同樣作法, 若將相臨的兩單位圓外接一長方形, 並連接長方形左下角及右上角可得一直線並將藍色區域分為兩塊, 定義下方那塊為橘色. 這次橘色區域面積約為藍色的 $36.46\%$.


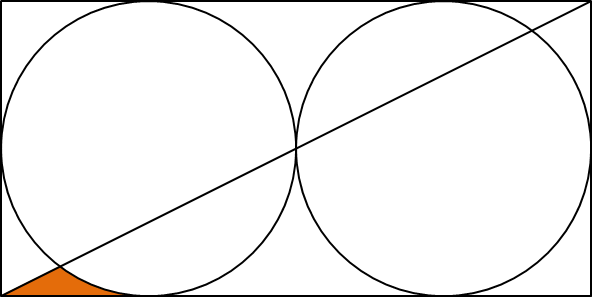
定義 $A(n)$ 為 $n$ 個水平相鄰單位圓照以上作法所切出之橘色面積與藍色面積的比值.

> 寫一函數, 此函數 `input` 為 $n$, `output` 為 $A(n)$

> 面積計算需準確至小數點後第四位, 因此不可使用 Monte Carlo 方式求面積. 不過可使用數值積分或其他可精準控制精度的方式.

以紙筆寫下
1. 作法步驟
2. pseudo code

#### Remark: 1 & 2 可以分開寫, 也可以寫一起

---