# Linux 核心專題: 重做 fibdrv
> 執行人: [bonianlee](https://github.com/bonianlee/fibdrv)
> [專題解說錄影](https://youtu.be/gD8qEwLtwz8)
:::success
:question: 提問清單
* ?
:::
## 任務簡述
依據 [fibdrv](https://hackmd.io/@sysprog/linux2023-fibdrv) 作業規範,重新進行 (刪去原有的 GitHub repository,做更好的自己!)。
## TODO: 紀錄閱讀作業說明中所有的疑惑
閱讀 [fibdrv](https://hackmd.io/@sysprog/linux2023-fibdrv) 作業規範,包含「作業說明錄影」和「Code Review 錄影」,本著「誠實面對自己」的心態,在本頁紀錄所有的疑惑,並與授課教師預約討論。
過程中,彙整 [Homework3](https://hackmd.io/@sysprog/linux2023-homework3) 學員的成果,挑選至少三份開發紀錄,提出值得借鏡之處,並重現相關實驗。
## TODO: 回覆「自我檢查清單」
回答「自我檢查清單」的所有問題,需要附上對應的參考資料和必要的程式碼,以第一手材料 (包含自己設計的實驗) 為佳
## TODO: 以 [sysprog21/bignum](https://github.com/sysprog21/bignum) 為範本,實作有效的大數運算
理解其中的技巧並導入到 fibdrv 中,並留意以下:
* 在 Linux 核心模組中,可用 ktime 系列的 API;
* 在 userspace 可用 clock_gettime 相關 API;
* 善用統計模型,除去極端數值,過程中應詳述你的手法
* 分別用 gnuplot 製圖,分析 Fibonacci 數列在核心計算和傳遞到 userspace 的時間開銷,單位需要用 us 或 ns (自行斟酌)
## TODO: 儘量降低由核心傳遞到應用程式的資料量
確保應用程式不需要過多的計算量才可重現 Fibonacci 數列,並需要充分驗證 fibdrv 行為。
## 時間測量與效能分析
分析程式的運行時間,可以作為性能好壞的判斷標準之一。使用 `ktime_t` 中的 `ktime_get()` 來紀錄在 kernel 中運行的時間,並經由 `ktime_sub()` 來計算經歷的時間長,方法如下
```c
static ktime_t kt;
```
計算 Fibonacci 是在 `fib_read()` 中進行,因此在此函式中計算運行時間
```c
static ssize_t fib_read(struct file *file,
char *buf,
size_t size,
loff_t *offset)
{
ktime_t start = ktime_get();
long long bn = fib_sequence(*offset);
kt = ktime_sub(ktime_get(), start);
return (ssize_t) bn;
}
```
參考 [yanjiew1](https://hackmd.io/@yanjiew/linux2023q1-fibdrv#%E6%95%88%E8%83%BD%E5%88%86%E6%9E%90%E5%B7%A5%E5%85%B7%E8%A8%AD%E5%AE%9A%E8%88%87%E6%B8%AC%E8%A9%A6) 的時間測量程式,將結果寫入 `TimeTaken.txt` 中,再匯入 Python 繪製數據圖

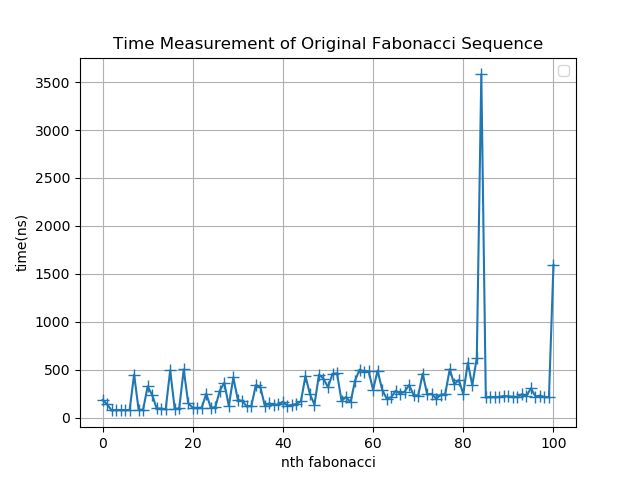
由圖形可以發現,隨著數列要計算的值越大,運算時間也會花費越多。另外,因為目前還沒有實作大數運算,因此在 Fibonacci sequence 第 92 個數字之後的計算耗時呈現定值
:::info
上面的數據圖是 `fib_sequence()` 尚未修正 Variable-length array (VLA) 在 Linux kernel 中不被允許的問題所繪製的圖,因為我將原本的陣列改為動態陣列後,雖然解決了 VLA 的問題,但是繪製出的圖形較不易看出趨勢,並且因為持續佔用記憶體的關係,導致運算時間較沒有一致性
:::
### User space 時間測量
可以使用 `time.h` 的 `clock_gettime` 在 user space 中進行時間測量。取得的時間即為 `struct timespec` ,其定義如下
```c
struct timespec {
time_t tv_sec; /* seconds */
long tv_nsec; /* nanoseconds */
};
```
若要將此結構的時間轉成 `ktime_t` ,只需要將時間單位都換成奈秒 (ns) 再相加即可,因為 `ktime_t` 是奈秒級別的結構
```c
clock_gettime(CLOCK_MONOTONIC, &t);
long long time = (long long) (t.tv_sec * 1e9 + t.tv_nsec);
```

從繪製出的數據圖發現有幾個極端的數據點,導致數據圖較缺乏參考價值。因此參考 < [用統計手法去除極端值](https://hackmd.io/@sysprog/linux2023-fibdrv-c#%E7%94%A8%E7%B5%B1%E8%A8%88%E6%89%8B%E6%B3%95%E5%8E%BB%E9%99%A4%E6%A5%B5%E7%AB%AF%E5%80%BC) > ,利用實作 [4ce43c4](https://github.com/colinyoyo26/fibdrv/commit/4ce43c4e7ee0b80c4ce9e6dcd995bbfdf239206c) 來將極端值去除,並且將 user space , kernel 以及 kernel to user 的時間花費圖放在一起做比較

理論上, kernel 的運算時間會較少, user space 的運算時間因為有經過資料傳輸,會比 kernel 還要多。從數值圖判斷,測量到的時間趨勢理論上是正確的。
:::info
在參考的程式碼中有一行 code 寫到
```c
Ys.append(np.delete(output, 0, axis=1))
```
`Ys` 是圖中三個數據所組成的 array ,而上面這行 code 在做的事情是將刪除 $n = 0$ 的數據加入 `Ys` 中。一開始我不解為何要刪掉第一項數據,因此我就將沒有刪除的數據再畫一次圖

發現第一項數據會是極端值,因此先做數據刪除的動作。但還是不確定為何不會自動被 `outlier_filter()` 給濾掉
:::
## 改進費氏數列計算方式
研讀〈[費氏數列](https://hackmd.io/@sysprog/linux2023-fibdrv-a#-%E8%B2%BB%E6%B0%8F%E6%95%B8%E5%88%97)〉,知道費氏數列有多種不同的計算方法,這邊簡述其中三種方式
1. 公式解
$$F(n) = \frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^n-\frac{1}{\sqrt{5}}(\frac{1-\sqrt{5}}{2})^n$$
這種方法的缺點是 $\sqrt{5}$ 無法在計算時得到確切的數值,因此隨著 $n$ 的值增加,次方項的誤差也會跟著增加
2. 遞迴加法
$$F(k) = F(k-1) + F(k-2)$$
這種算法雖然最基本與直觀,但不是聰明的方式。因為要計算 $F(k)$ 必須將第 $2$ 項到第 $k-1$ 項的數值都計算過一遍,而且每次求新的值都需要重複進行這樣的計算,運算量並沒有進行改善
3. Fast doubling
$$
\begin{bmatrix}
F(2) \\
F(1)
\end{bmatrix}
= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}
\begin{bmatrix}
F(1) \\
F(0)
\end{bmatrix} $$
$$\to\ \begin{bmatrix}
F(n+1) \\
F(n)
\end{bmatrix}
= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^{n}
\begin{bmatrix}
F(1) \\
F(0)
\end{bmatrix} $$
$$\to\ \begin{bmatrix}
F(2n+1) \\
F(2n)
\end{bmatrix}
= \begin{bmatrix}
1 & 1 \\
1 & 0
\end{bmatrix}^{2n}
\begin{bmatrix}
F(1) \\
F(0)
\end{bmatrix} $$
$$\to\ \begin{bmatrix}
F(2n+1) \\
F(2n)
\end{bmatrix}
= \begin{bmatrix}
F(n+1) & F(n) \\
F(n) & F(n-1)
\end{bmatrix}
\begin{bmatrix}
F(n+1) & F(n) \\
F(n) & F(n-1)
\end{bmatrix}
\begin{bmatrix}
1 \\
0
\end{bmatrix} $$
$$\to\ \begin{bmatrix}
F(2n+1) \\
F(2n)
\end{bmatrix}
= \begin{bmatrix}
F(n+1)^2 + F(n)^2 \\
F(n)F(n+1) + F(n)F(n-1)
\end{bmatrix} $$
$$\to\ \begin{bmatrix}
F(2n+1) \\
F(2n)
\end{bmatrix}
= \begin{bmatrix}
F(n+1)^2 + F(n)^2 \\
F(n)[2F(n+1) - F(n)]
\end{bmatrix}
$$
Fast doubling 的概念是只進行必要的運算,不會將目標項以前的每一個數值都計算出來。從上式 $F(2n+1)=F(n+1)^2 + F(n)^2$ 與 $F(2n) = F(n)[2F(n+1) - F(n)]$ 可以知道,想要求出 $F(2n+1)$ 與 $F(2n)$ 只需要用到 $F(n+1)$ 跟 $F(n)$ 項,計算量比遞迴加法少了一半以上
---
### Fast doubling 實作
參考 [fewletter](https://hackmd.io/@fewletter/linux2023q1-fibdrv) 的實作,將 Fast doubling 的概念以下方程式碼呈現
```c
for (uint64_t i = 1LL << 63; i; i >>= 1) {
long long n0 = f[0] * (2 * f[1] - f[0]);
long long n1 = f[0] * f[0] + f[1] * f[1];
if (k & i) {
f[0] = n1;
f[1] = n0 + n1;
}
else {
f[0] = n0;
f[1] = n1;
}
```
再次進行時間測量,得到下方數據圖

相較於先前的遞迴加法,從數據圖中不難發現計算時間受費氏數列項次的影響盛微,並且 kernel to user 的傳輸時間降低了不少,使得 user space 的耗費時間壓在 1050 奈秒左右,至少比遞迴加法所耗費的時間少了 450 奈秒
## 支援大數運算
礙於資料型態的空間限制, `long long` 只能儲存 64 位元的資料大小,若費氏數列的值超過 `long long` 所能夠儲存的範圍,則會發生溢位。為了支援大數運算,可以加入以下結構體
```c
typedef struct _bn {
unsigned int *number;
unsigned int size;
} bn;
```
在結構體中,將大數以 $2^{32}$ 為一個單位做進位, `size` 則儲存單位的數目
而為了要表示資料大小比 `long long` 還要大的數值,必須具備以下條件
- [預先計算儲存 $F(n)$ 所需的空間](https://hackmd.io/@sysprog/linux2023-fibdrv/%2F%40sysprog%2Flinux2023-fibdrv-b#%E9%A0%90%E5%85%88%E8%A8%88%E7%AE%97%E5%84%B2%E5%AD%98-Fn-%E6%89%80%E9%9C%80%E7%9A%84%E7%A9%BA%E9%96%93)
透過公式法先計算出 $F(n)$ 所需使用的位元數
$$
F(n) bit = \frac{-1160964 + 694242*n}{10^6} + 1
$$
```c
int fibn_per_32bit(int k)
{
return k < 2 ? 1 : ((long) k * 694242 - 1160964) / (1000000) + 1;
}
```
- [建立 `bn` 結構體](https://hackmd.io/@sysprog/linux2023-fibdrv-d#%E5%88%9D%E6%AD%A5%E6%94%AF%E6%8F%B4%E5%A4%A7%E6%95%B8%E9%81%8B%E7%AE%97)
```c
bn *bn_alloc(size_t size)
{
bn *new = kmalloc(sizeof(bn), GFP_KERNEL);
new->number = kmalloc(sizeof(int) * size, GFP_KERNEL);
memset(new->number, 0, sizeof(int) * size);
new->size = size;
return new;
}
```
- 清除 `bn`
```c
int bn_free(bn *src)
{
if (src == NULL)
return -1;
kfree(src->number);
kfree(src);
return 0;
}
```
---
### [`bn` 運算](https://hackmd.io/@sysprog/linux2023-fibdrv-d#%E5%88%9D%E6%AD%A5%E6%94%AF%E6%8F%B4%E5%A4%A7%E6%95%B8%E9%81%8B%E7%AE%97)
- `bn_add`
$2^{32}$ 進位的加法,先算低位元的加法,用 unsigned long long int 去儲存結果,若有進位的數值,則會在右移 32 位元之後出現
```c
void bn_add(bn *a, bn *b, bn *c)
{
unsigned long long int carry = 0;
for (int i = 0; i < c->size; i++) {
unsigned int tmp1 = (i < a->size) ? a->number[i] : 0;
unsigned int tmp2 = (i < b->size) ? b->number[i] : 0;
carry += (unsigned long long int) tmp1 + tmp2;
c->number[i] = carry;
carry >>= 32;
}
}
```
- `bn_swap`
互換兩個 `bn` 的位置,常用於迭代
```c
void bn_swap(bn *a, bn *b)
{
bn tmp = *a;
*a = *b;
*b = tmp;
}
```
- `bn_to_string`
將數字和 `0` 的差以 char 陣列儲存,並且從高位逐一檢查是否有進位,若有進位則處理成沒有進位的數字
```c
char *bn_to_string(bn src)
{
size_t len = (8 * sizeof(int) * src.size) / 3 + 2;
char *s = kmalloc(len, GFP_KERNEL);
char *p = s;
memset(s, '0', len - 1);
s[len - 1] = '\0';
for (int i = src.size - 1; i >= 0; i--) {
for (unsigned int d = 1U << 31; d; d >>= 1) {
/* binary -> decimal string */
int carry = !!(d & src.number[i]);
for (int j = len - 2; j >= 0; j--) {
s[j] += s[j] - '0' + carry; // double it
carry = (s[j] > '9');
if (carry)
s[j] -= 10;
}
}
}
// skip leading zero
while (p[0] == '0' && p[1] != '\0') {
p++;
}
memmove(s, p, strlen(p) + 1);
return s;
}
```
---
### 將 `bn` 加入費氏數列的運算
參考[程式碼](https://hackmd.io/@sysprog/linux2023-fibdrv-d#%E6%AD%A3%E7%A2%BA%E8%A8%88%E7%AE%97-F92-%E4%BB%A5%E5%BE%8C%E7%9A%84%E6%95%B8%E5%80%BC)將 `bn` 加入費氏數列的計算
```c
void bn_fib(bn *ret, unsigned int n)
{
int nsize = fibn_per_32bit(n) / 32 + 1;
bn_resize(ret, nsize);
if (n < 2) {
ret->number[0] = n;
return;
}
bn *f1 = bn_alloc(nsize);
bn *tmp = bn_alloc(nsize);
ret->number[0] = 0;
f1->number[0] = 1;
for (unsigned int i = 1; i < n + 1; i++) {
bn_add(ret, f1, tmp);
bn_swap(f1, ret);
bn_swap(f1, tmp);
}
bn_free(f1);
bn_free(tmp);
}
```
接著將加入大數運算的程式進行時間測量,把 $n$ 設為 1000 觀察數據圖的趨勢

從結果來看,此圖形是合理的。隨著計算量變大,運算時間也跟著拉長,同時因為資料傳輸量變大的緣故, user space 所耗費的時間相比於在 kernel 進行運算要長很多
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet