# [2020q3](http://wiki.csie.ncku.edu.tw/sysprog/schedule) 第 10 週測驗題
###### tags: `sysprog2020`
:::info
目的: 檢驗學員對 [Arm 處理器](https://beta.hackfoldr.org/arm/)及 [dynamic programming](https://en.wikipedia.org/wiki/Dynamic_programming) 的認知
:::
==[作答表單](https://docs.google.com/forms/d/e/1FAIpQLSdiBT5bRCO7LCGUn5Pcz9FjM2II08gmPcPe_EwImSCkjBjagA/viewform)==
### 測驗 `1`
:::info
針對「灰色」,美式英語常用 "gray" 拼法,英式英語則慣用 "grey" 拼法,兩者同義。
:::
給定每個像素 (pixel) 為 32-bit 的 RGBA 的位元圖 (bitmap),RGBA 代表紅綠藍三原色的首字母,Alpha 值則表示顏色的透明度/不透明度,其轉換為灰階影像 (gray scale) 的函式為:
```cpp
void rgba_to_bw(uint32_t *bitmap, int width, int height, long stride) {
int row, col;
uint32_t pixel, r, g, b, a, bw;
for (row = 0; row < height; row++) {
for (col = 0; col < width; col++) {
pixel = bitmap[col + row * stride / 4];
a = (pixel >> 24) & 0xff;
r = (pixel >> 16) & 0xff;
g = (pixel >> 8) & 0xff;
b = pixel & 0xff;
bw = (uint32_t) (r * 0.299 + g * 0.587 + b * 0.114);
bitmap[col + row * stride / 4] = (a << 24) + (bw << 16) + (bw << 8) + (bw);
}
}
}
```
人類視網膜包含三類錐形對光敏感的細胞,分別對不同波長範圍的光有反應:

> 上圖中的縱軸代表人眼對某對應波長的光的敏感度。其中 1 Å (埃) = $10^{–10}$ 米 = **0.1 nm** [[出處](http://www.phy.ntnu.edu.tw/demolab/html.php?html=everydayPhysics/color)]
人眼吸收綠色比其他顏色敏感,也可說人眼最容易捕捉到綠色,所以當影像變成灰階時,僅僅將紅色、綠色、藍色加總取平均,不足以反映出人眼所見。常見的方法是將 $Red \times 77, Green \times 151, Blue \times 28$,這三個除數的總和為 `256` (即 $2^8$),可使除法變簡單 (等同於右移 8 位元)。
如果我們將所有的運算都建立表格,於是
```cpp
bwPixel = table[rgbPixel & 0x00ffffff] + rgbPixel & 0xff000000;
```
$\to$ 16 MB; 表格太大
如果先計算針對「乘上 0.299」一類的運算,計算後建立表格呢?
```cpp
bw = (uint32_t) mul_299[r] + (uint32_t) mul_587[g] + (uint32_t) mul_144[b];
bitmap[col + row * strike / 4] = (a << 24) + (bw << 16) + (bw << 8) + bw;
```
$\to$ 降到 32 KB 以內; cache friendly
接著嘗試使用 NEON 指令集加速。將 RGB 三色的權重存入 r3, r4, r5 等暫存器。
`vdup.8` (Vector Duplicate),分別複製到大小為 8 bit 的 NEON register d0 - d2
```cpp
mov r3, #77
mov r4, #151
mov r5, #28
vdup.8 d0, r3
vdup.8 d1, r4
vdup.8 d2, r5
```
`vld4.8` (Vector Load),載入 pixel 的資料到 4 個 8-bit 的 NEON register d4-d7,其中那個 `4` 為 interleave,因為我們有 ARGB,所以 gap = 4。
再來就是計算 weighted average。可用 Vector Multiply 和 Vector Multiply Accumulate 指令:
```cpp
@ (alpha,R,G,B) = (d7,d6,d5,d4)
vld4.8 {d4-d7}, [r0]!
vmull.u8 q10, d6, d0
vmlal.u8 q10, d5, d1
vmlal.u8 q10, d4, d2
```
將值除以 256 就是我們要的灰階值。
`vrshrn` (Vector Shift Right by immediate value)
> vrshrn.u16 d4, q10, #8
最後儲存結果。
`vst` (Vector Store)
> vst4.8 {d4-d7}, [r3]!
效能評比如下: (對照 `v0` 和 `v4`)
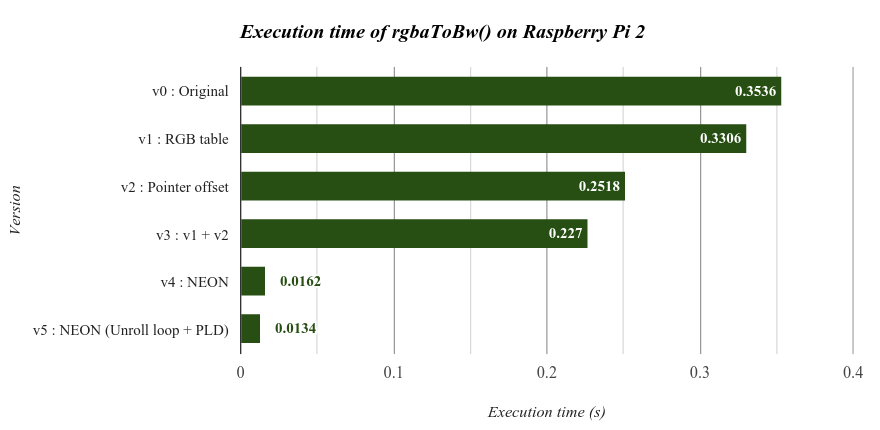
從這張表即可理解,使用 NEON 指令加速只用原本 4.6% 的時間即可完成 RGBA 轉灰階的處理。
[Neon Intrinsics](https://developer.arm.com/architectures/instruction-sets/simd-isas/neon/intrinsics) 允許我們避免直接撰寫組合語言,而是有如 C 函式呼叫,例如 `vmull.u8` 和 `vmlal.u8` 分別對應以下 intrinsics: (提示: 在 [Neon Intrinsics](https://developer.arm.com/architectures/instruction-sets/simd-isas/neon/intrinsics) 網頁搜尋 NEON intrinsics 可獲得更詳盡的描述)
* [vmull_u8](https://developer.arm.com/architectures/instruction-sets/simd-isas/neon/intrinsics?search=vmull_u8)
* [vmlal_u8](https://developer.arm.com/architectures/instruction-sets/simd-isas/neon/intrinsics?search=vmlal_u8)
考慮以下使用 `float` 來保存像素的程式碼:
```cpp
#include <stdint.h>
#define MIN(a, b) (((a) < (b)) ? (a) : (b))
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
uint8_t *to_rgb(const float *m, int w, int h, uint8_t *rgb)
{
int size = w * h;
const float *ptr0 = m + (0 * size);
const float *ptr1 = m + (1 * size);
const float *ptr2 = m + (2 * size);
uint8_t *ret = rgb;
#define SATURATE_CAST_UCHAR(X) (uint8_t) MIN(MAX((int) (X), 0), 255);
for (int remain = size; remain > 0; remain--) {
rgb[0] = SATURATE_CAST_UCHAR(*ptr0);
rgb[1] = SATURATE_CAST_UCHAR(*ptr1);
rgb[2] = SATURATE_CAST_UCHAR(*ptr2);
rgb += 3;
ptr0++, ptr1++, ptr2++;
}
#undef SATURATE_CAST_UCHAR
return ret;
}
```
函式 `to_rgb` 可將原本透過連續的 `float` 空間保存的資料轉為 RGB 像素,每個像素佔用 3 個位元組,即 24 位元。針對 Aarch64 (Arm 64-bit) 架構 (假設為 little-endian),下方的程式碼則可將 RGB 轉換為灰階:
```cpp
#include <arm_neon.h>
float *rgb_to_gray(const uint8_t *rgb, int w, int h, float *m)
{
const uint8_t Y_shift = 8;
const uint8_t R2Y = 77, G2Y = 151, B2Y = 28;
float *ptr = m;
int size = w * h;
int nn = size >> 3;
int remain = size - (nn << 3);
uint8x8_t _R2Y = vdup_n_u8(R2Y);
uint8x8_t _G2Y = vdup_n_u8(G2Y);
uint8x8_t _B2Y = vdup_n_u8(B2Y);
for (; nn > 0; nn--) {
uint8x8x3_t _rgb = vld3_u8(rgb);
uint16x8_t y16 = vmull_u8(_rgb.val[0], _R2Y);
y16 = vmlal_u8(y16, _rgb.val[1], _G2Y);
y16 = vmlal_u8(y16, _rgb.val[2], _B2Y);
y16 = vshrq_n_u16(y16, Y_shift);
float32x4_t _ylow = vcvtq_f32_u32(vmovl_u16(vget_low_u16(y16)));
float32x4_t _yhigh = vcvtq_f32_u32(vmovl_u16(vget_high_u16(y16)));
vst1q_f32(ptr + OFFSET1, _ylow);
vst1q_f32(ptr + OFFSET2, _yhigh);
rgb += 3 * 8, ptr += 8;
}
for (; remain > 0; remain--) {
*ptr = (rgb[0] * R2Y + rgb[1] * G2Y + rgb[2] * B2Y) >> Y_shift;
rgb += 3, ptr++;
}
return m;
}
```
請補完程式碼,使上述程式碼得以符合預期地運作。
==作答區==
OFFSET1 = ?
* `(a)` (-4)
* `(b)` (-2)
* `(c)` (-1)
* `(d)` 0 (o)
* `(e)` 1
* `(f)` 2
* `(g)` 4
OFFSET2 = ?
* `(a)` (-4)
* `(b)` (-2)
* `(c)` (-1)
* `(d)` 0
* `(e)` 1
* `(f)` 2
* `(g)` 4 (o)
:::success
延伸問題:
1. 整合 [libattopng](https://github.com/misc0110/libattopng),輸出 RGBA 和灰階的 PNG 圖片
* 可能會用到 [ImageMagick](https://imagemagick.org/) 事先處理輸入檔案
* 參照 [Bomb Lab 實作紀錄](https://hackmd.io/@posutsai/SyNzl72f4) 得知如何安裝 GNU Toolchain 及 QEMU
2. 引入 loop unrolling 和 prefetch 指令,嘗試改進 NEON 程式碼效率
* 你需要在真實的 Arm 硬體上進行實驗,如 [Raspberry Pi](https://www.raspberrypi.org/) 3 (或更新的硬體)
:::
---
### 測驗 `2`
LeetCode [1617. Count Subtrees With Max Distance Between Cities](https://leetcode.com/problems/count-subtrees-with-max-distance-between-cities/) 給定 $n$ 個城市,編號為從 $1$ 到 $n$,再給予一個大小為 $n-1$ 的陣列 `edges`,其中 $edges[i] = [u_i, v_i]$ 表示城市 $u_i$ 和 $v_i$ 之間存在雙向邊。題目保證任意城市之間有唯一的路徑,也就是說所有城市構成一棵樹 (tree)。

> 上圖的連通關係為:
> * $1,4$
> * $1,3$
> * $3,2$
> * $1,3,2$
> * $4,1,3$
> * $4,1,3,2$
一棵子樹 (subtree) 是上述所有城市的子集,在子集中,任意城市間可透過子集的其他城市和邊到達。兩個子樹被認為不一樣的條件是,至少有個城市在其中一棵子樹中存在,卻又不存在於另一棵子樹中。
給定 $d$ 範圍介於從 $1$ 到 $n-1$,請你找出城市間最大距離恰好為 $d$ 的所有子樹數目。請你回傳一個大小為 $n-1$ 的陣列,其中第 $d$ 個元素(下標從 1 開始)是城市間最大距離恰好等於 $d$ 的子樹數目。
> 兩個城市間距離定義是,它們之間需要經過的邊的數目。

第一組輸入:
* n = 4
* edges = $[[1,2],[2,3],[2,4]]$
預期輸出:
* $[3,4,0]$
> 既然 $n = 4$,於是輸出的陣列會有 3 個元素
> 1. 子樹 `{1,2}`, `{2,3}` 和 `{2,4}` 最大距離都為 1
> 2. 子樹 `{1,2,3}`, `{1,2,4}`, `{2,3,4}` 和 `{1,2,3,4}` 最大距離都為 `2`
> 3. 不存在城市間最大距離為 `3` 的子樹。
第二組輸入:
* n = 2
* edges = $[[1,2]]$
預期輸出:
* $[1]$
> 既然 $n = 2$,於是輸出的陣列只存在 1 個元素,且題目已保證任意城市之間只有唯一的路徑
第三組輸入:
* n = 3
* edges = $[[1,2],[2,3]]$
預期輸出:
* $[2,1]$
> 既然 $n = 3$,於是輸出的陣列會有 2 個元素
> 1. 子樹 `{1,2}` 和 `{2,3}` 最大距離都為 `1`
> 2. 子樹 `{1,2,3}` 最大距離為 `2`
限制:
* $2 \le n \le 15$
* edges.length == $n-1$
* edges[i].length == 2
* $1 \le u_i, v_i \le n$
* 題目保證 $(u_i, v_i)$ 所表示的邊互不相同
思路:
* 因為 $n \le 15$,所以就往狀態壓縮 + [dynamic programming](https://en.wikipedia.org/wiki/Dynamic_programming) 的技巧去思考,但本題之間狀態間的轉移無法進行,只能窮舉所有情況
* 本題的樹可看成是無向無環連通圖(二者等價)
> 在圖論中,環是一條只有第一個和最後一個頂點重複的非空路徑
> * 不具備環的圖被稱作無環圖
> * 不具備有向環的有向圖被稱做有向無環圖 (DAG,directed acyclic graph)
> * 無環的連通圖被稱作樹
> 
* 窮舉狀態,首先要判斷是否無效
1. 該狀態僅有 $1$ 個節點,因題目要求的 $d$ 最小是 $1$,即距離為 $1$,所以可縮減
2. 該狀態下不是一個子樹,即非一個連通圖,那怎麼判斷是否是連通圖呢?可利用 BFS 或 DFS 判斷所能到達的節點的個數,是否和集合內元素個數 (二進位 $1$ 的個數)相同即可
* 判斷該狀態是有效後,如何求最大距離?所謂的最大距離是無向無環連通圖的最大直徑
以下程式碼是針對 LeetCode [1617. Count Subtrees With Max Distance Between Cities](https://leetcode.com/problems/count-subtrees-with-max-distance-between-cities/) 提出可能的解法:
```cpp=
#include <stdint.h>
#include <stdlib.h>
#include <string.h>
#define MIN(a, b) (((a) < (b)) ? (a) : (b))
#define ITERATE(i, begin, end) \
for (int i = (begin), i##_end_ = (end); i < i##_end_; i++)
int *countSubgraphsForEachDiameter(int n,
int **edges,
int edgesSz,
int *edges0sz,
int *rsz)
{
uint8_t d[n][n]; /* distance */
memset(d, 0xFF, sizeof(d));
uint16_t conn[n];
ITERATE (i, 0, n)
conn[i] = 1 << i;
for (int z = 0; z < edgesSz; z++) {
int *e = edges[z];
int u = e[0] - 1, v = e[1] - 1;
d[u][v] = d[v][u] = 1;
conn[u] |= 1 << v, conn[v] |= 1 << u;
}
ITERATE (k, 0, n)
ITERATE (i, 0, n)
ITERATE (j, 0, n)
d[i][j] = MIN(d[i][j], d[i][k] + d[k][j]);
int *rv = calloc(n - 1, sizeof(int));
ITERATE (S, 1, (1 << n)) {
int ctmp = 1 << __builtin_ctz(S);
while (1) {
int conn_nxt = ctmp;
ITERATE (d, 0, n)
if ((ctmp >> d) & 1)
conn_nxt |= conn[d];
conn_nxt &= S;
if (COND1)
break;
ctmp = conn_nxt;
}
if (COND2)
continue;
uint8_t ret = 0;
ITERATE (i, 0, n)
if ((S >> i) & 1)
ITERATE (j, 0, i)
if (((S >> j) & 1) && (ret < d[i][j]))
ret = d[i][j];
if (!ret)
continue;
rv[ITER]++;
}
*rsz = n - 1;
return rv;
}
```
參考資訊
* [花花醬解說: Count Subtrees With Max Distance Between Cities](https://youtu.be/qag7m9VRf-A)
* [Bit manipulation and diameter of a tree](https://jimmy-shen.medium.com/bit-manipulation-and-diameter-of-a-tree-3856d549c5f8)
請補完程式碼,使上述程式碼得以符合預期地運作。
==作答區==
COND1 = ?
* `(a)` `conn_nxt == ctmp`
* `(b)` `conn_nxt != ctmp`
* `(c)` `conn_nxt >= ctmp`
* `(d)` `conn_nxt`
COND2 = ?
* `(a)` `ctmp`
* `(b)` `!ctmp`
* `(c)` `~ctmp & S`
* `(d)` `ctmp & ~S`
* `(e)` `ctmp ^ S`
ITER = ?
* `(a)` `++ret`
* `(b)` `--ret`
* `(c)` `ret++`
* `(d)` `ret--`
* `(e)` `ret`
:::success
延伸問題:
1. 解釋上述程式碼運作原理,指出改進方式
2. 用 C99/C11 (可搭配 GNU extension) 重新實作符合 LeetCode 要求但效率優於上述表現的實作,一併分析時間複雜度。
:::
---
 Sign in with Wallet
Sign in with Wallet
 Sign in with Wallet
Sign in with Wallet